沪科版(八年级数学下册 19.3.1矩形 试题(2课时 含答案)
文档属性
| 名称 | 沪科版(八年级数学下册 19.3.1矩形 试题(2课时 含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 308.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-05 00:00:00 | ||
图片预览

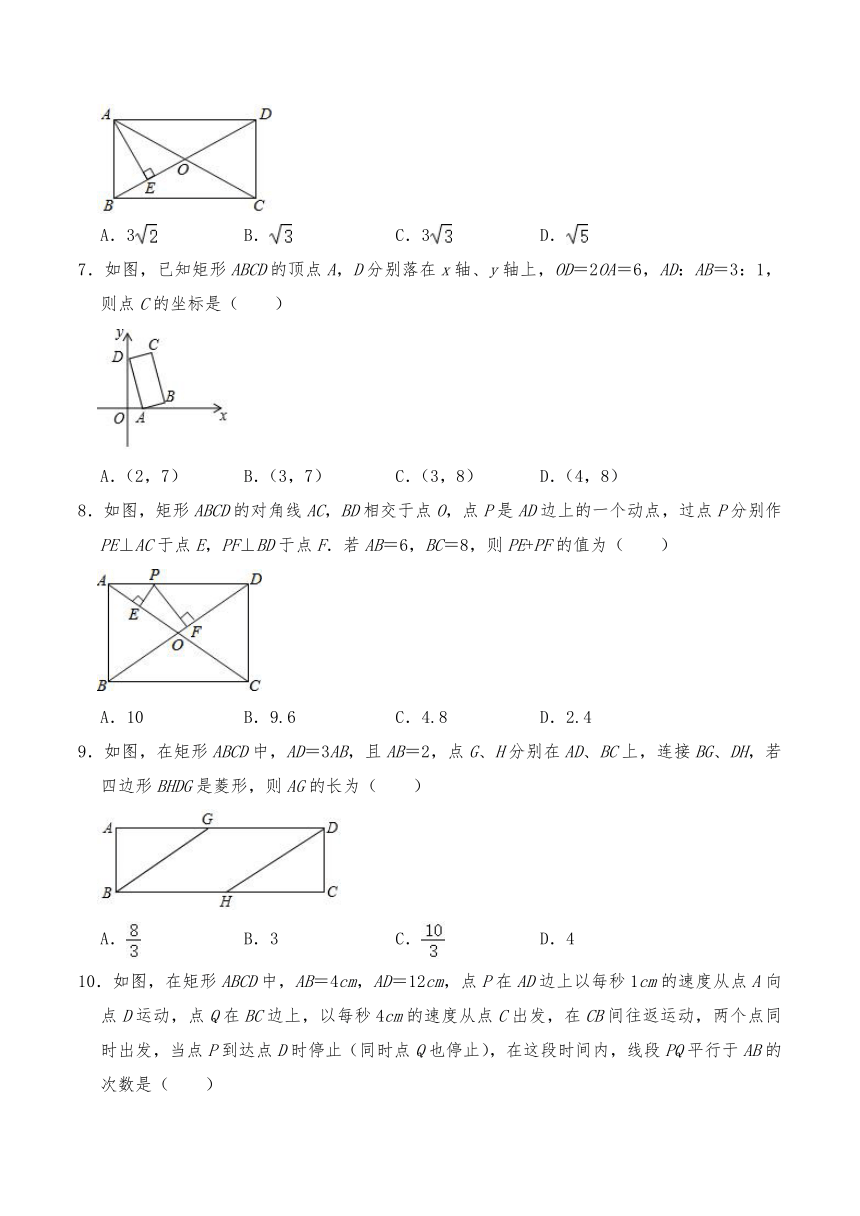
文档简介
19.3.1矩形
第1课时矩形的性质
一、选择题
1.一个矩形的两条对角线的一个夹角为60°,对角线长为16cm,则这个矩形较短边的长为( )
A.2cm B.4cm C.8cm D.16cm
2.矩形ABCD中,与AC相等的线段是( )
A.BA B.BC C.BD D.CD
3.如图,矩形ABCD中,对角线AC,BD交于点O,若∠AOB=60°,BD=8,则DC长为( )
A.4 B.4 C.3 D.5
4.如图,在矩形ABCD中,AC,BD相交于点O,若△AOB的面积是3,则矩形ABCD的面积是( )
A.6 B.9 C.12 D.15
5.如图,在矩形ABCD中,AE平分∠BAD交BC于点E,连接ED,若ED=5,EC=3,则长方形的面积为( )
A.15 B.16 C.22 D.28
6.如图,在矩形ABCD中,AB=1,对角线AC与BD相交于点O,AE⊥BD,垂足为E,若BE=EO,则AD的长是( )
A.3 B. C.3 D.
7.如图,已知矩形ABCD的顶点A,D分别落在x轴、y轴上,OD=2OA=6,AD:AB=3:1,则点C的坐标是( )
A.(2,7) B.(3,7) C.(3,8) D.(4,8)
8.如图,矩形ABCD的对角线AC,BD相交于点O,点P是AD边上的一个动点,过点P分别作PE⊥AC于点E,PF⊥BD于点F.若AB=6,BC=8,则PE+PF的值为( )
A.10 B.9.6 C.4.8 D.2.4
9.如图,在矩形ABCD中,AD=3AB,且AB=2,点G、H分别在AD、BC上,连接BG、DH,若四边形BHDG是菱形,则AG的长为( )
A. B.3 C. D.4
10.如图,在矩形ABCD中,AB=4cm,AD=12cm,点P在AD边上以每秒1cm的速度从点A向点D运动,点Q在BC边上,以每秒4cm的速度从点C出发,在CB间往返运动,两个点同时出发,当点P到达点D时停止(同时点Q也停止),在这段时间内,线段PQ平行于AB的次数是( )
A.2 B.3 C.4 D.5
填空题
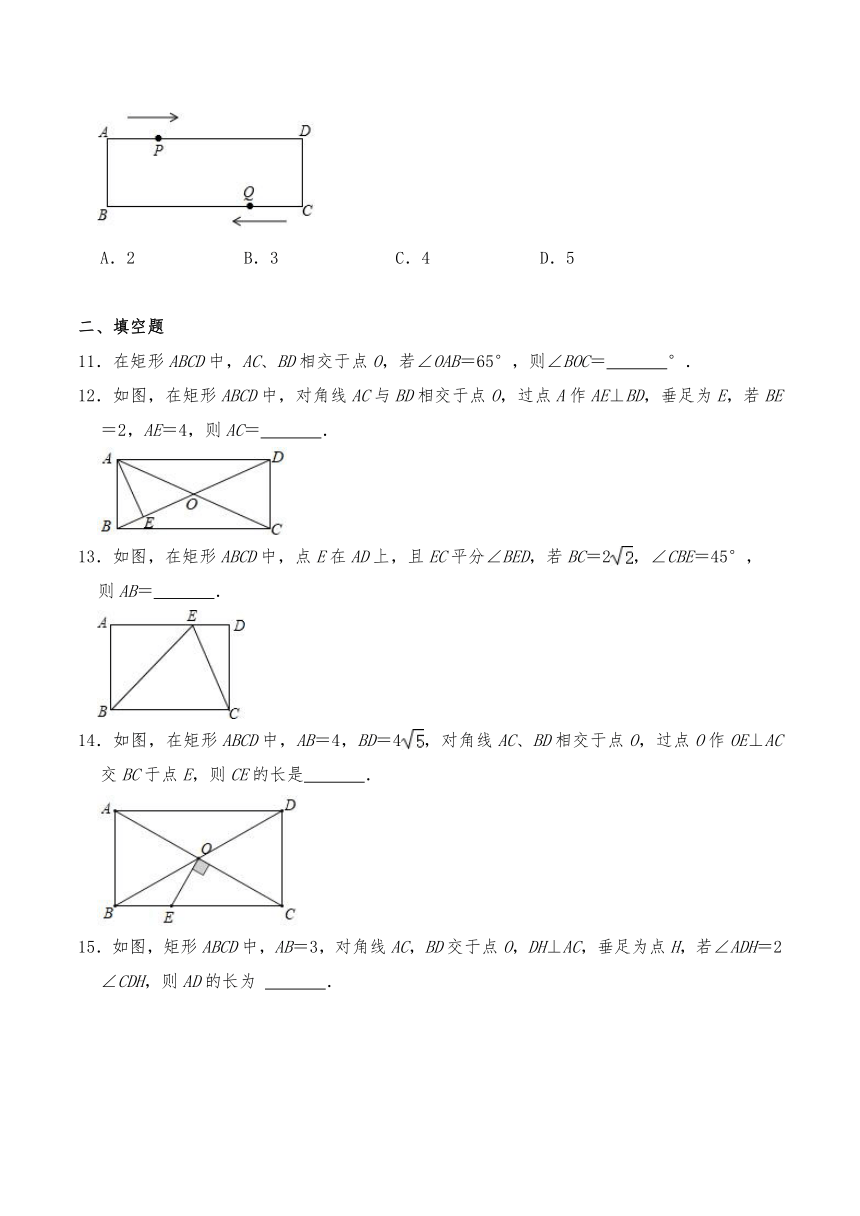
11.在矩形ABCD中,AC、BD相交于点O,若∠OAB=65°,则∠BOC= °.
12.如图,在矩形ABCD中,对角线AC与BD相交于点O,过点A作AE⊥BD,垂足为E,若BE=2,AE=4,则AC= .
13.如图,在矩形ABCD中,点E在AD上,且EC平分∠BED,若BC=2,∠CBE=45°,
则AB= .
14.如图,在矩形ABCD中,AB=4,BD=4,对角线AC、BD相交于点O,过点O作OE⊥AC交BC于点E,则CE的长是 .
15.如图,矩形ABCD中,AB=3,对角线AC,BD交于点O,DH⊥AC,垂足为点H,若∠ADH=2∠CDH,则AD的长为 .
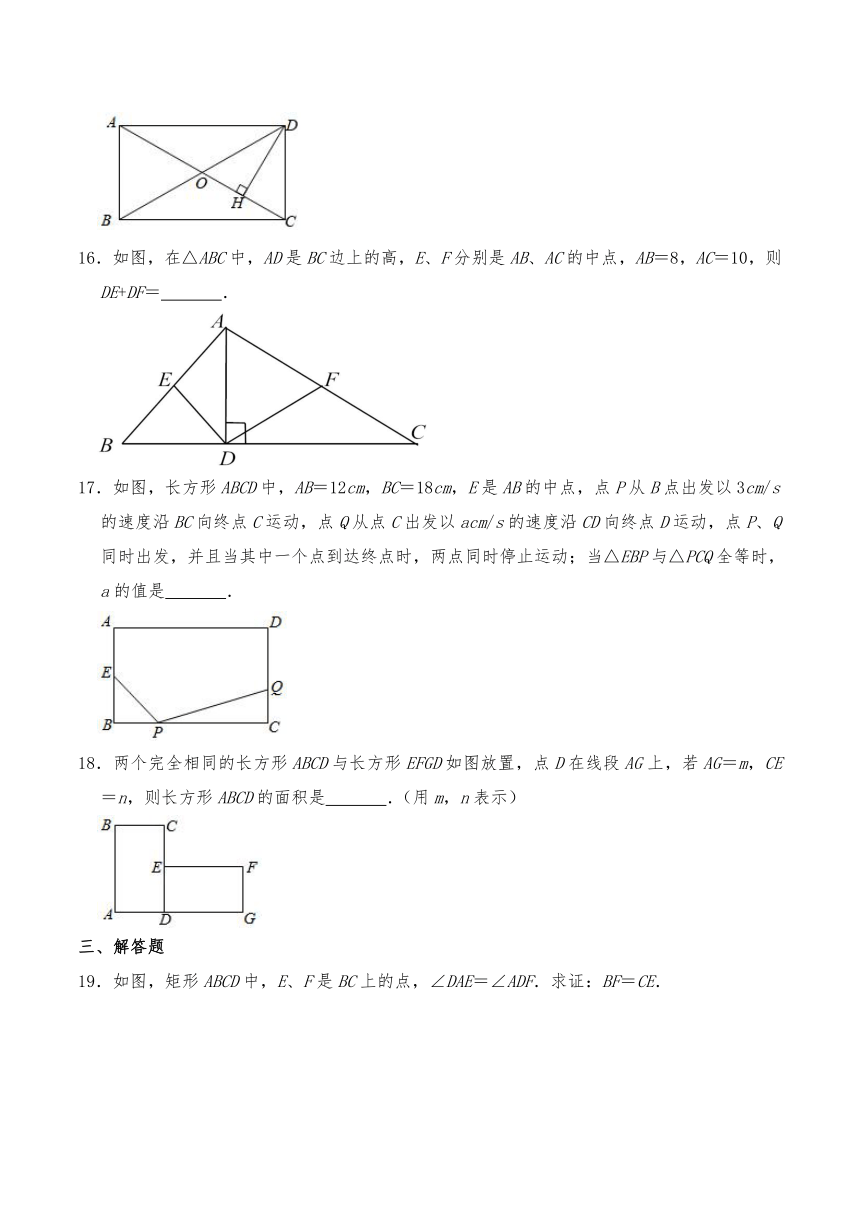
16.如图,在△ABC中,AD是BC边上的高,E、F分别是AB、AC的中点,AB=8,AC=10,则DE+DF= .
17.如图,长方形ABCD中,AB=12cm,BC=18cm,E是AB的中点,点P从B点出发以3cm/s的速度沿BC向终点C运动,点Q从点C出发以acm/s的速度沿CD向终点D运动,点P、Q同时出发,并且当其中一个点到达终点时,两点同时停止运动;当△EBP与△PCQ全等时,a的值是 .
18.两个完全相同的长方形ABCD与长方形EFGD如图放置,点D在线段AG上,若AG=m,CE=n,则长方形ABCD的面积是 .(用m,n表示)
三、解答题
19.如图,矩形ABCD中,E、F是BC上的点,∠DAE=∠ADF.求证:BF=CE.
20.如图,矩形ABCD中,AB=1,BC=2,点E在AD上,点F在BC边上,FE平分∠DFB.
(1)判断△DEF的形状,并说明理由;
(2)若点F是BC的中点,求AE的长.
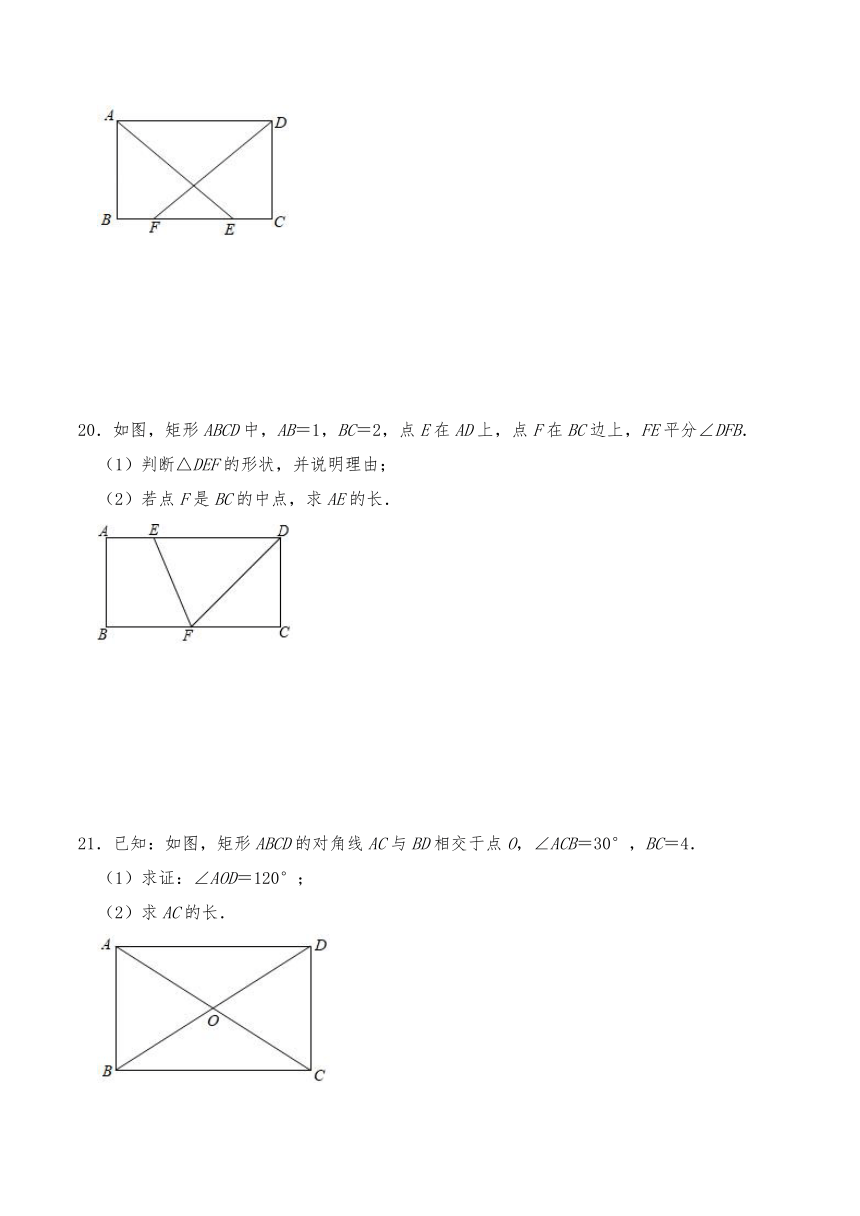
21.已知:如图,矩形ABCD的对角线AC与BD相交于点O,∠ACB=30°,BC=4.
(1)求证:∠AOD=120°;
(2)求AC的长.
22.如图,已知点E在矩形ABCD的边DC上,且AB=AE=2AD.求∠EBC的度数.
23.如图,在 ABCD中,将对角线BD分别向两个方向延长至点E、F,且BE=DF.连接AF、CF、CE、AE.
(1)求证:四边形AECF是平行四边形;
(2)若AD=4,BE=3,∠ADB=∠CBD=90°,当四边形AECF是矩形时,则BD的长为 .
24.如图,矩形ABCD中,AB=BC,在边AB上截取BE,使得BE=BC,连接CE,作DF⊥EC于点F,连接BF并延长交AD于点G,连接DE.
(1)求证:DE平分∠AEC;
(2)若AD=,求出DG的长.
第2课时矩形的判定
一、选择题
1.已知四边形ABCD为平行四边形,要使四边形ABCD为矩形,则可增加条件为( )
A.AB=BC B.AC=BD C.AC⊥BD D.AC平分∠BAD
2.如图, ABCD的对角线相交于点O,下列条件中能判定这个平行四边形是矩形的是( )
A.AC=BD B.AB=BC C.∠BAC=∠CAD D.AC⊥BD
3.如图,四边形ABCD为平行四边形,延长AD到点E,使DE=AD连接EB,EC,DB.添加一个条件,不能使四边形DBCE成为矩形的是( )
A.AB=BE B.∠ADB=90° C.BE⊥DC D.CE⊥DE
4.甲、乙、丙、丁四位同学到木工厂参观时,木工师傅拿尺子要他们帮助检测一个窗框是否是矩形,他们各自做了如下检测,检测后,他们都说窗框是矩形,你认为正确的是( )
A.甲量得窗框两组对边分别相等
B.乙量得窗框对角线相等
C.丙量得窗框的一组邻边相等
D.丁量得窗框的两组对边分别相等且两条对角线相等
5.如图,在平行四边形ABCD中,对角线AC、BD相交于点O,则下面条件能判断平行四边形ABCD是矩形的是( )
A.AC=BD B.AC⊥BD C.AO=CO D.AB=AD
6.如图,要使 ABCD成为矩形,需添加的条件是( )
A.AB=BC B.∠ABC=90° C.AC⊥BD D.∠1=∠2
7.如图,在四边形ABCD中,已知AD∥BC,∠BCD=90°,∠ABC=45°,BD平分∠ABC,若CD=1cm,则AC等于( )
A. B. C.2cm D.1cm
8.如图, ABCD的对角线AC、BD交于点O,顺次连接 ABCD各边中点得到一个新的四边形,如果添加下列四个条件中的一个条件:①AC⊥BD;②C△ABO=C△CBO;③∠DAO=∠CBO;④∠DAO=∠BAO,可以使这个新的四边形成为矩形,那么这样的条件个数是( )
A.1个 B.2个 C.3个 D.4个
9.如图,在直角三角形ABC中,∠ACB=90°,AC=3,BC=4,点M是边AB上一点(不与点A,B重合),作ME⊥AC于点E,MF⊥BC于点F,若点P是EF的中点,则CP的最小值是( )
A.1.2 B.1.5 C.2.4 D.2.5
10.如图,在△ABC中,∠C=90°,AC=8,BC=6,点P为斜边AB上一动点,过点P作PE⊥AC于点E,PF⊥BC于点F,连结EF,则线段EF的最小值为( )
A.1.2 B.2.4 C.2.5 D.4.8
填空题
11.如图,在四边形ABCD中,AC与BD相交于点O,且OA=OC,OB=OD,请你添加一个条件,使四边形ABCD为矩形,你添加的条件是 (填一个即可).
12.如图,在四边形ABCD中,AB=DC,AD=BC,请再添加一个条件,使四边形ABCD是矩形.你添加的条件是 .(写出一种即可)
13.在四边形ABCD中,有以下四个条件:
①AB∥CD;②AD=BC;③AC=BD;④∠ADC=∠ABC.
从中选取三个条件,可以判定四边形ABCD为矩形.则可以选择的条件序号是 .
14.已知Rt△ABC,∠ABC=90°,小明按如下步骤作图,①以A为圆心,BC长为半径作弧,以C为圆心,AB长为半径作弧,两弧相交于点D;②连接DA,DC,则四边形ABCD为 .
15.如图,四边形ABCD的对角线互相平分,需要添加一个条件,使它变为矩形,你添加的条件是 .(不要添加任何字母和辅助线)
16.如图,在矩形ABCD中,AB=4cm,AD=12cm,点P从点A向点D以每秒1cm的速度运动,Q以每秒4cm的速度从点C出发,在B、C两点之间做往返运动,两点同时出发,点P到达点D为止(同时点Q也停止),这段时间内,当运动时间为 时,P、Q、C、D四点组成矩形.
17.如图,在平行四边形ABCD中,若∠1=∠2,则四边形ABCD是 .
18.如图,点E,F,G,H分别是BD,BC,AC,AD的中点:下列结论:①EH=EF;②当AB=CD,EG平分∠HGF;③当AB⊥CD时,四边形EFGH是矩形;其中正确的结论序号是 .
三、解答题
19.如图,在△ABC中,∠ABC=90°,点O是斜边AC的中点,过点O作OE⊥AC,交AB于点E,过点A作AD∥BC,与BO的延长线交于点D,连接CD、DE.
(1)求证:四边形ABCD是矩形;
(2)若BC=3,∠BAC=30°,求DE的长.
20.如图,在△ABC中,AB=AC,D是BC中点,过点A作AE∥BC,使AE=BD.
(1)求证:四边形AEBD是矩形;
(2)取AB中点F,作GF⊥AB,交EB于点G,若AD=8,BD=4,求EG的长.
21.如图,已知点M,O,N在同一直线上,OB,OC分别是∠AOM与∠AON的平分线,AB⊥OB,AC⊥OC,垂足分别为B,C,连接BC交AO于点E.
(1)求证:四边形ACOB是矩形.
(2)猜想BC与MN的位置关系,并证明你的结论.
22.如图,△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.
(1)判断OE与OF的大小关系?并说明理由;
(2)当点O运动到何处时,四边形AECF是矩形?并说出你的理由;
23.如图,在 ABCD中,E、G分别是AB、CD的中点,且AH=CF,AH∥CF.
(1)求证:△AEH≌△CGF;
(2)连接FH,HG,EF,若FH=AD,求证:四边形EFGH是矩形.
24.如图,在四边形ABCD中,AC、BD相交于点O,AD∥BC,∠ADC=∠ABC,OA=OB.
(1)如图1,求证:四边形ABCD为矩形;
(2)如图2,P是AD边上任意一点,PE⊥BD,PF⊥AC,E、F分别是垂足,若AD=12,AB=5,求PE+PF的值.
第1课时答案
一、选择题
C.C.B.C.D.B.A.C.A.C.
二、填空题
11.130. 12.10. 13.2. 14.5. 15.3.
16.9. 17.3或2. 18..
三、解答题
19.证明:∵四边形ABCD是矩形,
∴AD∥BC,∠B=∠C=90°,AB=CD,
∴∠DAE=∠BEA,∠ADF=∠CFD,
又∵∠DAE=∠ADF,
∴∠BEA=∠CFD,
在△BEA和△CFD中,
,
∴△BEA≌△CFD(AAS),
∴BE=CF,
∴BF=CE.
20.解:(1)△DEF是等腰三角形,
理由如下:∵四边形ABCD是矩形,
∴AB=CD,AD=BC,AD∥BC,∠C=90°,
∴∠BFE=∠DEF,
∵FE平分∠DFB,
∴∠BFE=∠DFE,
∴∠DEF=∠DFE,
∴DE=DF,
∴△DEF是等腰三角形;
(2)∵AB=1,BC=2,
∴CD=1,AD=2,
∵点F是BC的中点,
∴FC==1,
Rt△DCF中,∠C=90°,
∴DF=,
∴DE=DF=,
∴AE=AD﹣DE=2﹣.
21.(1)证明:∵四边形ABCD是矩形,
∴AC=BD,AO=CO=AC,BO=DO=BD,
∴BO=CO,
∴∠OBC=∠OCB,
∵∠ACB=30°,
∴∠OBC=30°,
∵∠OBC+∠OCB+∠BOC=180°,
∴∠BOC=120°,
∴∠AOD=∠BOC=120°;
(2)∵四边形ABCD是矩形,
∴∠ABC=90°,
∵∠ACB=30°,
∴AB=AC,即AC=2AB,
∵AB2+BC2=AC2,BC=4,
解得AB=,
∴AC=.
22.解:如图所示:
∵四边形ABCD是矩形,
∴DC∥AB,∠ABC=∠ADC=90°,
∵AE=2AD,
∴∠AED=30°,
∵DC∥AB,
∴∠EAB=∠AED=30°,
∵AB=AE,
∴∠ABE=∠AEB=(180°﹣∠EAB)=75°,
∵∠ABC=90°,
∴∠EBC=∠ABC﹣∠ABE=90°﹣75°=15°.
23.(1)证明:连接AC,
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵BE=DF,
∴OE=OF,
∴四边形AECF是平行四边形.
(2)解:BE=DF=3,
∵∠ADB=∠CBD=90°,
∴AF==5,
方法1:∵AD=4,
∴BC=4,
设OB=x,则OE=x+3,
∵四边形AECF是矩形,
∴OE=OC=x+3,
∵∠OBC=90°,
在Rt△OBC中,
OB2+BC2=OC2,
∴x2+42=(x+3)2,
解得x=,
∴OB=,
∴BD=.
方法2:∵四边形AECF是矩形,
∴∠FAE=90°,
∴∠FAE=∠ADF,
∵∠AFD=∠EFA,
∴△FAD∽△FEA(AA),
∴=,即=,
解得FE=,
∴BD=﹣3﹣3=.
故答案为:.
24.解:(1)∵四边形ABCD是矩形,
∴AB=CD,AB∥DC,∠ABC=90°,
∵BC=BE,
∴CE=BC,
∵AB=BC,
∴CD=CE,∴∠CDE=∠CED,
∵AB∥CD,
∴∠CDE=∠AED,
∴∠AED=∠DEC,
∴DE平分∠AEC;
(2)∵BC=BE,∠CBE=90°,
∴∠BCE=∠BEC=45°,
∵CD∥AB,
∴∠DCE=∠BEC=45°,
∵DF⊥CE,
∴∠CDF=45°,
∴DF=CF,
∴CD=DF,
∵AB=CD,AB=,BC=BE,
∴BE=DF=CF=BC,
∵∠ADC=90°,
∴∠FDG=45°,
∴∠BEF=∠EDF,
∵BC=CF,∠BCF=45°,
∴∠CBF=∠CFB=67.5°,
∴∠EBF=90°﹣67.5°=22.5°,
∠DFG=180°﹣67.5°﹣90°=22.5°,
∴∠EBF=∠DFG,
在△DFG和△EBF中,
∴△DFG≌△EBF(ASA),
∴DG=EF,
∵EF=CE﹣CF=AB﹣BC=,
∴DG=2.
第2课时答案
一、选择题
B.A.C.D.A.B.B.C.A.D.
二、填空题
11.OA=OB(答案不唯一).12.对角线相等(答案不唯一). 13.①③④.
14.矩形.
15.AC=BD或∠ABC=90°或∠BCD=90°或∠CDA=90°或∠DAB=90°.
16.2.4s或4s或7.2s. 17.矩形. 18.②③.
三、解答题
19.(1)证明:∵点O是AC的中点,
∴OA=OC,
∵AD∥BC,
∴∠DAO=∠BCO,∠ADO=∠CBO,
在△OAD与△OCB中,
,
∴△OAD≌△OCB(AAS),
∴AD=BC,
∵AD∥BC,
∴四边形ABCD是平行四边形,
∵∠ABC=90°,
∴平行四边形ABCD是矩形;
(2)解:∵四边形ABCD是矩形,
∴AD=BC=3,
∵∠ABC=90°,∠BAC=30°,
∴AC=2BC=6,
∴OA=3,
∵OE⊥AC,
∴∠AOE=90°,
∵∠BAC=30°,
∴OE=OA=,
∴AE=2OE=2,
∴DE===.
20.(1)证明:AE∥BC,AE=BD,
∴四边形AEBD是平行四边形,
∵AB=AC,D是BC中点,
∴AD⊥BC,
∴∠ADB=90°,
∴四边形AEBD是矩形;
(2)解:连接AG,
∵F是AB的中点,GF⊥AB,
∴GA=GB,
∵四边形AEBD是矩形,AD=8,BD=4,
∴EB=AD=8,EA=BD=4,
设EG=x,则GB=GA=8﹣x,
∵四边形AEBD是矩形,
∴∠E=90°,
在Rt△AEG中,
∵EA2+EG2=AG2,
∴42+x2=(8﹣x)2,
∴x=3,
即EG=3.
21.(1)证明:∵OB,OC分别是∠AOM与∠AON的平分线,
∴∠AOM=2∠AOB,∠AON=2∠AOC,
∵点M,O,N在同一直线上,
∴∠AOM+∠AON=180°,
∴2∠AOB+2∠AOC=180°,
∴∠AOB+∠AOC=90°,
∴∠BOC=90°,
∵AB⊥OB,AC⊥OC,
∴∠ABO=∠ACO=90°=∠BOC,
∴四边形ACOB是矩形;
(2)解:BC∥MN,证明如下:
由(1)知,四边形ACOB是矩形,
∴OE=CE,
∴∠AOC=∠BCO,
∵OC是∠AON的角平分线,
∴∠AOC=∠NOC,
∴∠BCO=∠NOC,
∴BC∥MN.
22.解:(1)OE=OF,理由如下:
∵MN∥BC,
∴∠OEC=∠ECB,
∵CE平分∠ACB,
∴∠ACE=∠ECB,
∴∠OEC=∠ACE,
∴OE=OC,
同理可得:OC=OF,
∴OE=OF;
(2)当O为AC中点时,四边形AECF是矩形;
理由如下:
∵OA=OC,OE=OF(已证),
∴四边形AECF是平行四边形,
∵EC平分∠ACB,CF平分∠ACG,
∴∠ACE=∠ACB,∠ACF=∠ACG,
∴∠ACE+∠ACF=(∠ACB+∠ACG)=×180°=90°,
即∠ECF=90°,
∴四边形AECF是矩形.
23.证明:(1)延长AH交CD于点P,延长CF交AB于Q,如图所示:
∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴AQ∥CP,
∵AH∥CF,
∴四边形APCQ是平行四边形,
∴∠HAE=∠FCG,
∵E、G分别是AB、CD的中点,
∴AE=AB,CG=CD,
∴AE=CG,
在△AHE和△CFG中,,
∴△AHE≌△CFG(SAS);
(2)连接FH、EG,
∵AH∥CF,
∴∠AHF=∠HFC,
由(1)得:∠AHE=∠CFG,HE=FG,
∴∠AHF﹣∠AHE=∠HFC﹣∠CFG,即∠EHF=∠GFH,
∴HE∥FG,
∴四边形EFGH是平行四边形,
由(1)得:AE=DG,AB∥CD,
∴四边形ADGE是平行四边形,
∴AD=EG,
又∵FH=AD,
∴EG=FH,
∴四边形EFGH是矩形.
24.证明:(1)∵AD∥BC,
∴∠ABC+∠BAD=180°,∠ADC+∠BCD=180°,
∵∠ABC=∠ADC,
∴∠BAD=∠BCD,
∴四边形ABCD是平行四边形,
∴OA=OC=AC,OB=OD=BD,
∵OA=OB,
∴AC=BD,
∴四边形ABCD是矩形;
(2)如图,连接OP,
∵AD=12,AB=5,
∴BD===13,
∴BO=OD=AO=CO=,
∵S△AOD=S矩形ABCD=×12×5=15,
∴S△AOP+S△POD=15,
∴××FP+××EP=15,
∴PE+PF=.
第1课时矩形的性质
一、选择题
1.一个矩形的两条对角线的一个夹角为60°,对角线长为16cm,则这个矩形较短边的长为( )
A.2cm B.4cm C.8cm D.16cm
2.矩形ABCD中,与AC相等的线段是( )
A.BA B.BC C.BD D.CD
3.如图,矩形ABCD中,对角线AC,BD交于点O,若∠AOB=60°,BD=8,则DC长为( )
A.4 B.4 C.3 D.5
4.如图,在矩形ABCD中,AC,BD相交于点O,若△AOB的面积是3,则矩形ABCD的面积是( )
A.6 B.9 C.12 D.15
5.如图,在矩形ABCD中,AE平分∠BAD交BC于点E,连接ED,若ED=5,EC=3,则长方形的面积为( )
A.15 B.16 C.22 D.28
6.如图,在矩形ABCD中,AB=1,对角线AC与BD相交于点O,AE⊥BD,垂足为E,若BE=EO,则AD的长是( )
A.3 B. C.3 D.
7.如图,已知矩形ABCD的顶点A,D分别落在x轴、y轴上,OD=2OA=6,AD:AB=3:1,则点C的坐标是( )
A.(2,7) B.(3,7) C.(3,8) D.(4,8)
8.如图,矩形ABCD的对角线AC,BD相交于点O,点P是AD边上的一个动点,过点P分别作PE⊥AC于点E,PF⊥BD于点F.若AB=6,BC=8,则PE+PF的值为( )
A.10 B.9.6 C.4.8 D.2.4
9.如图,在矩形ABCD中,AD=3AB,且AB=2,点G、H分别在AD、BC上,连接BG、DH,若四边形BHDG是菱形,则AG的长为( )
A. B.3 C. D.4
10.如图,在矩形ABCD中,AB=4cm,AD=12cm,点P在AD边上以每秒1cm的速度从点A向点D运动,点Q在BC边上,以每秒4cm的速度从点C出发,在CB间往返运动,两个点同时出发,当点P到达点D时停止(同时点Q也停止),在这段时间内,线段PQ平行于AB的次数是( )
A.2 B.3 C.4 D.5
填空题
11.在矩形ABCD中,AC、BD相交于点O,若∠OAB=65°,则∠BOC= °.
12.如图,在矩形ABCD中,对角线AC与BD相交于点O,过点A作AE⊥BD,垂足为E,若BE=2,AE=4,则AC= .
13.如图,在矩形ABCD中,点E在AD上,且EC平分∠BED,若BC=2,∠CBE=45°,
则AB= .
14.如图,在矩形ABCD中,AB=4,BD=4,对角线AC、BD相交于点O,过点O作OE⊥AC交BC于点E,则CE的长是 .
15.如图,矩形ABCD中,AB=3,对角线AC,BD交于点O,DH⊥AC,垂足为点H,若∠ADH=2∠CDH,则AD的长为 .
16.如图,在△ABC中,AD是BC边上的高,E、F分别是AB、AC的中点,AB=8,AC=10,则DE+DF= .
17.如图,长方形ABCD中,AB=12cm,BC=18cm,E是AB的中点,点P从B点出发以3cm/s的速度沿BC向终点C运动,点Q从点C出发以acm/s的速度沿CD向终点D运动,点P、Q同时出发,并且当其中一个点到达终点时,两点同时停止运动;当△EBP与△PCQ全等时,a的值是 .
18.两个完全相同的长方形ABCD与长方形EFGD如图放置,点D在线段AG上,若AG=m,CE=n,则长方形ABCD的面积是 .(用m,n表示)
三、解答题
19.如图,矩形ABCD中,E、F是BC上的点,∠DAE=∠ADF.求证:BF=CE.
20.如图,矩形ABCD中,AB=1,BC=2,点E在AD上,点F在BC边上,FE平分∠DFB.
(1)判断△DEF的形状,并说明理由;
(2)若点F是BC的中点,求AE的长.
21.已知:如图,矩形ABCD的对角线AC与BD相交于点O,∠ACB=30°,BC=4.
(1)求证:∠AOD=120°;
(2)求AC的长.
22.如图,已知点E在矩形ABCD的边DC上,且AB=AE=2AD.求∠EBC的度数.
23.如图,在 ABCD中,将对角线BD分别向两个方向延长至点E、F,且BE=DF.连接AF、CF、CE、AE.
(1)求证:四边形AECF是平行四边形;
(2)若AD=4,BE=3,∠ADB=∠CBD=90°,当四边形AECF是矩形时,则BD的长为 .
24.如图,矩形ABCD中,AB=BC,在边AB上截取BE,使得BE=BC,连接CE,作DF⊥EC于点F,连接BF并延长交AD于点G,连接DE.
(1)求证:DE平分∠AEC;
(2)若AD=,求出DG的长.
第2课时矩形的判定
一、选择题
1.已知四边形ABCD为平行四边形,要使四边形ABCD为矩形,则可增加条件为( )
A.AB=BC B.AC=BD C.AC⊥BD D.AC平分∠BAD
2.如图, ABCD的对角线相交于点O,下列条件中能判定这个平行四边形是矩形的是( )
A.AC=BD B.AB=BC C.∠BAC=∠CAD D.AC⊥BD
3.如图,四边形ABCD为平行四边形,延长AD到点E,使DE=AD连接EB,EC,DB.添加一个条件,不能使四边形DBCE成为矩形的是( )
A.AB=BE B.∠ADB=90° C.BE⊥DC D.CE⊥DE
4.甲、乙、丙、丁四位同学到木工厂参观时,木工师傅拿尺子要他们帮助检测一个窗框是否是矩形,他们各自做了如下检测,检测后,他们都说窗框是矩形,你认为正确的是( )
A.甲量得窗框两组对边分别相等
B.乙量得窗框对角线相等
C.丙量得窗框的一组邻边相等
D.丁量得窗框的两组对边分别相等且两条对角线相等
5.如图,在平行四边形ABCD中,对角线AC、BD相交于点O,则下面条件能判断平行四边形ABCD是矩形的是( )
A.AC=BD B.AC⊥BD C.AO=CO D.AB=AD
6.如图,要使 ABCD成为矩形,需添加的条件是( )
A.AB=BC B.∠ABC=90° C.AC⊥BD D.∠1=∠2
7.如图,在四边形ABCD中,已知AD∥BC,∠BCD=90°,∠ABC=45°,BD平分∠ABC,若CD=1cm,则AC等于( )
A. B. C.2cm D.1cm
8.如图, ABCD的对角线AC、BD交于点O,顺次连接 ABCD各边中点得到一个新的四边形,如果添加下列四个条件中的一个条件:①AC⊥BD;②C△ABO=C△CBO;③∠DAO=∠CBO;④∠DAO=∠BAO,可以使这个新的四边形成为矩形,那么这样的条件个数是( )
A.1个 B.2个 C.3个 D.4个
9.如图,在直角三角形ABC中,∠ACB=90°,AC=3,BC=4,点M是边AB上一点(不与点A,B重合),作ME⊥AC于点E,MF⊥BC于点F,若点P是EF的中点,则CP的最小值是( )
A.1.2 B.1.5 C.2.4 D.2.5
10.如图,在△ABC中,∠C=90°,AC=8,BC=6,点P为斜边AB上一动点,过点P作PE⊥AC于点E,PF⊥BC于点F,连结EF,则线段EF的最小值为( )
A.1.2 B.2.4 C.2.5 D.4.8
填空题
11.如图,在四边形ABCD中,AC与BD相交于点O,且OA=OC,OB=OD,请你添加一个条件,使四边形ABCD为矩形,你添加的条件是 (填一个即可).
12.如图,在四边形ABCD中,AB=DC,AD=BC,请再添加一个条件,使四边形ABCD是矩形.你添加的条件是 .(写出一种即可)
13.在四边形ABCD中,有以下四个条件:
①AB∥CD;②AD=BC;③AC=BD;④∠ADC=∠ABC.
从中选取三个条件,可以判定四边形ABCD为矩形.则可以选择的条件序号是 .
14.已知Rt△ABC,∠ABC=90°,小明按如下步骤作图,①以A为圆心,BC长为半径作弧,以C为圆心,AB长为半径作弧,两弧相交于点D;②连接DA,DC,则四边形ABCD为 .
15.如图,四边形ABCD的对角线互相平分,需要添加一个条件,使它变为矩形,你添加的条件是 .(不要添加任何字母和辅助线)
16.如图,在矩形ABCD中,AB=4cm,AD=12cm,点P从点A向点D以每秒1cm的速度运动,Q以每秒4cm的速度从点C出发,在B、C两点之间做往返运动,两点同时出发,点P到达点D为止(同时点Q也停止),这段时间内,当运动时间为 时,P、Q、C、D四点组成矩形.
17.如图,在平行四边形ABCD中,若∠1=∠2,则四边形ABCD是 .
18.如图,点E,F,G,H分别是BD,BC,AC,AD的中点:下列结论:①EH=EF;②当AB=CD,EG平分∠HGF;③当AB⊥CD时,四边形EFGH是矩形;其中正确的结论序号是 .
三、解答题
19.如图,在△ABC中,∠ABC=90°,点O是斜边AC的中点,过点O作OE⊥AC,交AB于点E,过点A作AD∥BC,与BO的延长线交于点D,连接CD、DE.
(1)求证:四边形ABCD是矩形;
(2)若BC=3,∠BAC=30°,求DE的长.
20.如图,在△ABC中,AB=AC,D是BC中点,过点A作AE∥BC,使AE=BD.
(1)求证:四边形AEBD是矩形;
(2)取AB中点F,作GF⊥AB,交EB于点G,若AD=8,BD=4,求EG的长.
21.如图,已知点M,O,N在同一直线上,OB,OC分别是∠AOM与∠AON的平分线,AB⊥OB,AC⊥OC,垂足分别为B,C,连接BC交AO于点E.
(1)求证:四边形ACOB是矩形.
(2)猜想BC与MN的位置关系,并证明你的结论.
22.如图,△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.
(1)判断OE与OF的大小关系?并说明理由;
(2)当点O运动到何处时,四边形AECF是矩形?并说出你的理由;
23.如图,在 ABCD中,E、G分别是AB、CD的中点,且AH=CF,AH∥CF.
(1)求证:△AEH≌△CGF;
(2)连接FH,HG,EF,若FH=AD,求证:四边形EFGH是矩形.
24.如图,在四边形ABCD中,AC、BD相交于点O,AD∥BC,∠ADC=∠ABC,OA=OB.
(1)如图1,求证:四边形ABCD为矩形;
(2)如图2,P是AD边上任意一点,PE⊥BD,PF⊥AC,E、F分别是垂足,若AD=12,AB=5,求PE+PF的值.
第1课时答案
一、选择题
C.C.B.C.D.B.A.C.A.C.
二、填空题
11.130. 12.10. 13.2. 14.5. 15.3.
16.9. 17.3或2. 18..
三、解答题
19.证明:∵四边形ABCD是矩形,
∴AD∥BC,∠B=∠C=90°,AB=CD,
∴∠DAE=∠BEA,∠ADF=∠CFD,
又∵∠DAE=∠ADF,
∴∠BEA=∠CFD,
在△BEA和△CFD中,
,
∴△BEA≌△CFD(AAS),
∴BE=CF,
∴BF=CE.
20.解:(1)△DEF是等腰三角形,
理由如下:∵四边形ABCD是矩形,
∴AB=CD,AD=BC,AD∥BC,∠C=90°,
∴∠BFE=∠DEF,
∵FE平分∠DFB,
∴∠BFE=∠DFE,
∴∠DEF=∠DFE,
∴DE=DF,
∴△DEF是等腰三角形;
(2)∵AB=1,BC=2,
∴CD=1,AD=2,
∵点F是BC的中点,
∴FC==1,
Rt△DCF中,∠C=90°,
∴DF=,
∴DE=DF=,
∴AE=AD﹣DE=2﹣.
21.(1)证明:∵四边形ABCD是矩形,
∴AC=BD,AO=CO=AC,BO=DO=BD,
∴BO=CO,
∴∠OBC=∠OCB,
∵∠ACB=30°,
∴∠OBC=30°,
∵∠OBC+∠OCB+∠BOC=180°,
∴∠BOC=120°,
∴∠AOD=∠BOC=120°;
(2)∵四边形ABCD是矩形,
∴∠ABC=90°,
∵∠ACB=30°,
∴AB=AC,即AC=2AB,
∵AB2+BC2=AC2,BC=4,
解得AB=,
∴AC=.
22.解:如图所示:
∵四边形ABCD是矩形,
∴DC∥AB,∠ABC=∠ADC=90°,
∵AE=2AD,
∴∠AED=30°,
∵DC∥AB,
∴∠EAB=∠AED=30°,
∵AB=AE,
∴∠ABE=∠AEB=(180°﹣∠EAB)=75°,
∵∠ABC=90°,
∴∠EBC=∠ABC﹣∠ABE=90°﹣75°=15°.
23.(1)证明:连接AC,
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵BE=DF,
∴OE=OF,
∴四边形AECF是平行四边形.
(2)解:BE=DF=3,
∵∠ADB=∠CBD=90°,
∴AF==5,
方法1:∵AD=4,
∴BC=4,
设OB=x,则OE=x+3,
∵四边形AECF是矩形,
∴OE=OC=x+3,
∵∠OBC=90°,
在Rt△OBC中,
OB2+BC2=OC2,
∴x2+42=(x+3)2,
解得x=,
∴OB=,
∴BD=.
方法2:∵四边形AECF是矩形,
∴∠FAE=90°,
∴∠FAE=∠ADF,
∵∠AFD=∠EFA,
∴△FAD∽△FEA(AA),
∴=,即=,
解得FE=,
∴BD=﹣3﹣3=.
故答案为:.
24.解:(1)∵四边形ABCD是矩形,
∴AB=CD,AB∥DC,∠ABC=90°,
∵BC=BE,
∴CE=BC,
∵AB=BC,
∴CD=CE,∴∠CDE=∠CED,
∵AB∥CD,
∴∠CDE=∠AED,
∴∠AED=∠DEC,
∴DE平分∠AEC;
(2)∵BC=BE,∠CBE=90°,
∴∠BCE=∠BEC=45°,
∵CD∥AB,
∴∠DCE=∠BEC=45°,
∵DF⊥CE,
∴∠CDF=45°,
∴DF=CF,
∴CD=DF,
∵AB=CD,AB=,BC=BE,
∴BE=DF=CF=BC,
∵∠ADC=90°,
∴∠FDG=45°,
∴∠BEF=∠EDF,
∵BC=CF,∠BCF=45°,
∴∠CBF=∠CFB=67.5°,
∴∠EBF=90°﹣67.5°=22.5°,
∠DFG=180°﹣67.5°﹣90°=22.5°,
∴∠EBF=∠DFG,
在△DFG和△EBF中,
∴△DFG≌△EBF(ASA),
∴DG=EF,
∵EF=CE﹣CF=AB﹣BC=,
∴DG=2.
第2课时答案
一、选择题
B.A.C.D.A.B.B.C.A.D.
二、填空题
11.OA=OB(答案不唯一).12.对角线相等(答案不唯一). 13.①③④.
14.矩形.
15.AC=BD或∠ABC=90°或∠BCD=90°或∠CDA=90°或∠DAB=90°.
16.2.4s或4s或7.2s. 17.矩形. 18.②③.
三、解答题
19.(1)证明:∵点O是AC的中点,
∴OA=OC,
∵AD∥BC,
∴∠DAO=∠BCO,∠ADO=∠CBO,
在△OAD与△OCB中,
,
∴△OAD≌△OCB(AAS),
∴AD=BC,
∵AD∥BC,
∴四边形ABCD是平行四边形,
∵∠ABC=90°,
∴平行四边形ABCD是矩形;
(2)解:∵四边形ABCD是矩形,
∴AD=BC=3,
∵∠ABC=90°,∠BAC=30°,
∴AC=2BC=6,
∴OA=3,
∵OE⊥AC,
∴∠AOE=90°,
∵∠BAC=30°,
∴OE=OA=,
∴AE=2OE=2,
∴DE===.
20.(1)证明:AE∥BC,AE=BD,
∴四边形AEBD是平行四边形,
∵AB=AC,D是BC中点,
∴AD⊥BC,
∴∠ADB=90°,
∴四边形AEBD是矩形;
(2)解:连接AG,
∵F是AB的中点,GF⊥AB,
∴GA=GB,
∵四边形AEBD是矩形,AD=8,BD=4,
∴EB=AD=8,EA=BD=4,
设EG=x,则GB=GA=8﹣x,
∵四边形AEBD是矩形,
∴∠E=90°,
在Rt△AEG中,
∵EA2+EG2=AG2,
∴42+x2=(8﹣x)2,
∴x=3,
即EG=3.
21.(1)证明:∵OB,OC分别是∠AOM与∠AON的平分线,
∴∠AOM=2∠AOB,∠AON=2∠AOC,
∵点M,O,N在同一直线上,
∴∠AOM+∠AON=180°,
∴2∠AOB+2∠AOC=180°,
∴∠AOB+∠AOC=90°,
∴∠BOC=90°,
∵AB⊥OB,AC⊥OC,
∴∠ABO=∠ACO=90°=∠BOC,
∴四边形ACOB是矩形;
(2)解:BC∥MN,证明如下:
由(1)知,四边形ACOB是矩形,
∴OE=CE,
∴∠AOC=∠BCO,
∵OC是∠AON的角平分线,
∴∠AOC=∠NOC,
∴∠BCO=∠NOC,
∴BC∥MN.
22.解:(1)OE=OF,理由如下:
∵MN∥BC,
∴∠OEC=∠ECB,
∵CE平分∠ACB,
∴∠ACE=∠ECB,
∴∠OEC=∠ACE,
∴OE=OC,
同理可得:OC=OF,
∴OE=OF;
(2)当O为AC中点时,四边形AECF是矩形;
理由如下:
∵OA=OC,OE=OF(已证),
∴四边形AECF是平行四边形,
∵EC平分∠ACB,CF平分∠ACG,
∴∠ACE=∠ACB,∠ACF=∠ACG,
∴∠ACE+∠ACF=(∠ACB+∠ACG)=×180°=90°,
即∠ECF=90°,
∴四边形AECF是矩形.
23.证明:(1)延长AH交CD于点P,延长CF交AB于Q,如图所示:
∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴AQ∥CP,
∵AH∥CF,
∴四边形APCQ是平行四边形,
∴∠HAE=∠FCG,
∵E、G分别是AB、CD的中点,
∴AE=AB,CG=CD,
∴AE=CG,
在△AHE和△CFG中,,
∴△AHE≌△CFG(SAS);
(2)连接FH、EG,
∵AH∥CF,
∴∠AHF=∠HFC,
由(1)得:∠AHE=∠CFG,HE=FG,
∴∠AHF﹣∠AHE=∠HFC﹣∠CFG,即∠EHF=∠GFH,
∴HE∥FG,
∴四边形EFGH是平行四边形,
由(1)得:AE=DG,AB∥CD,
∴四边形ADGE是平行四边形,
∴AD=EG,
又∵FH=AD,
∴EG=FH,
∴四边形EFGH是矩形.
24.证明:(1)∵AD∥BC,
∴∠ABC+∠BAD=180°,∠ADC+∠BCD=180°,
∵∠ABC=∠ADC,
∴∠BAD=∠BCD,
∴四边形ABCD是平行四边形,
∴OA=OC=AC,OB=OD=BD,
∵OA=OB,
∴AC=BD,
∴四边形ABCD是矩形;
(2)如图,连接OP,
∵AD=12,AB=5,
∴BD===13,
∴BO=OD=AO=CO=,
∵S△AOD=S矩形ABCD=×12×5=15,
∴S△AOP+S△POD=15,
∴××FP+××EP=15,
∴PE+PF=.
