河南新中考圆的计算与证明最后一练(含解析)
文档属性
| 名称 | 河南新中考圆的计算与证明最后一练(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 692.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-05 18:36:17 | ||
图片预览


文档简介
中考圆的计算与证明最后一练
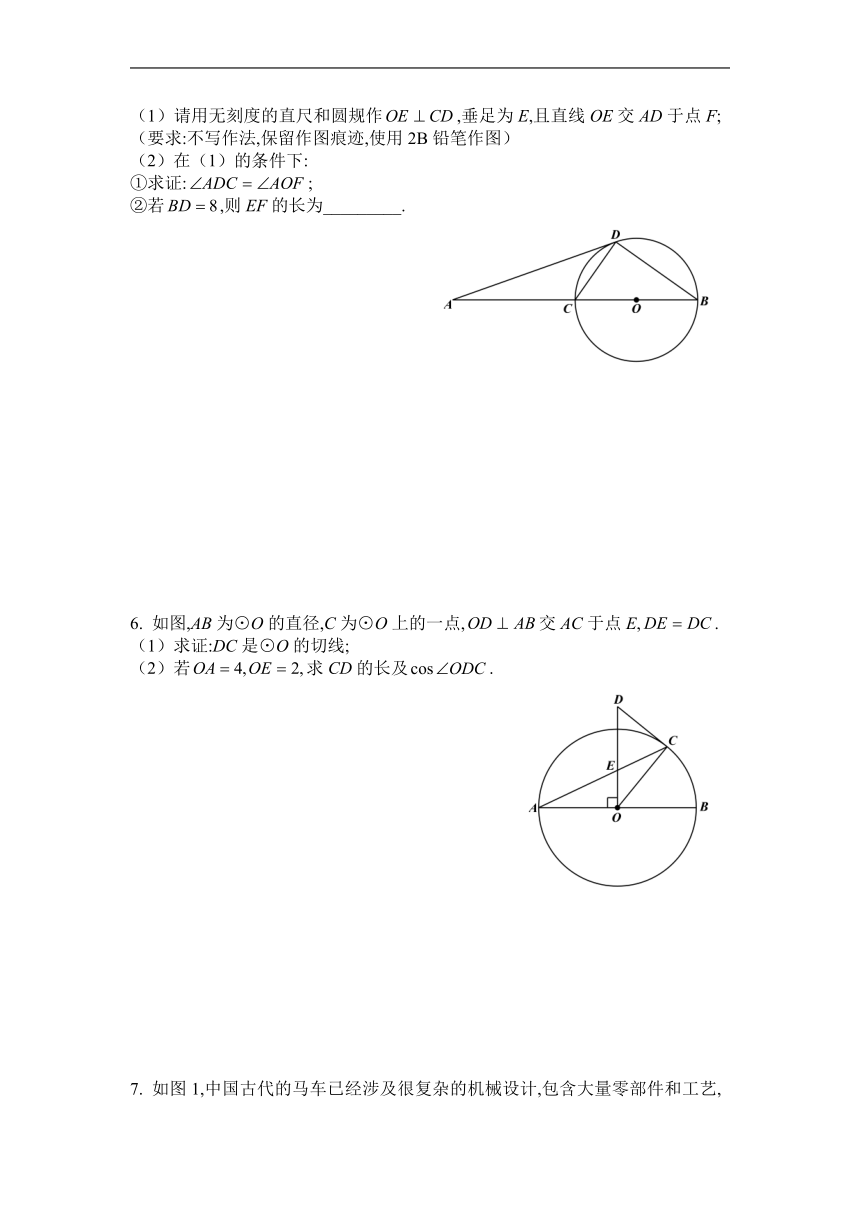
1. 如图,MN是⊙O的直径,A、B是⊙O上的两点,过点A作⊙O的切线交BN的延长线于点C,,连结AB、AM.
(1)求证:;
(2)若⊙O的半径为,求线段AC的长.
2. 如图所示,以AE为直径的⊙O与△ABC的边BC相切于点D,,连结AD、DE.
(1)求证:AD平分;
(2)尺规作图:在⊙O上找一点F,使DF平分;(不写作法,保留作图痕迹)
(3)若(2)中DF与AB交于点G,,求线段FG的长.
3. 如图所示,在Rt△ABC中,,点D在斜边BC上,直角边AC恰好与以BD为直径的半圆相切于点E,连结DE,过点O作,交AB于点F.
(1)请判断四边形BOEF的形状,并说明理由;
(2)若,求AB的长.
4. 如图,BC是⊙O的直径,CE是⊙O的弦,过点E作⊙O的切线,交CB的延长线于点G,过点B作于点F,交CE的延长线于点A.
(1)求证:;
(2)若,⊙O的半径是2,求AF的长.
5. 如图,点C为线段AB的中点,BC为⊙O的直径,AD为⊙O的切线,切点为D.
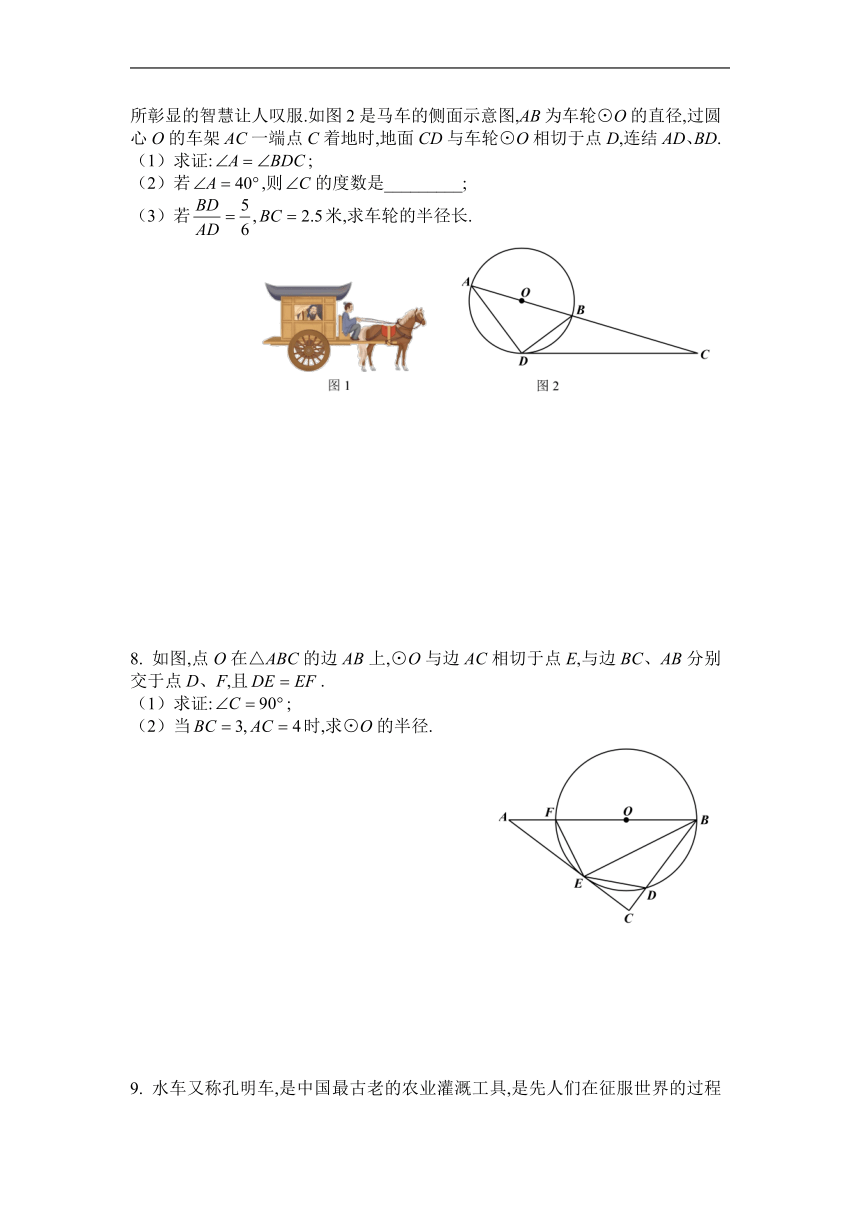
(1)请用无刻度的直尺和圆规作,垂足为E,且直线OE交AD于点F;(要求:不写作法,保留作图痕迹,使用2B铅笔作图)
(2)在(1)的条件下:
①求证:;
②若,则EF的长为_________.
6. 如图,AB为⊙O的直径,C为⊙O上的一点,交AC于点E,.
(1)求证:DC是⊙O的切线;
(2)若求CD的长及.
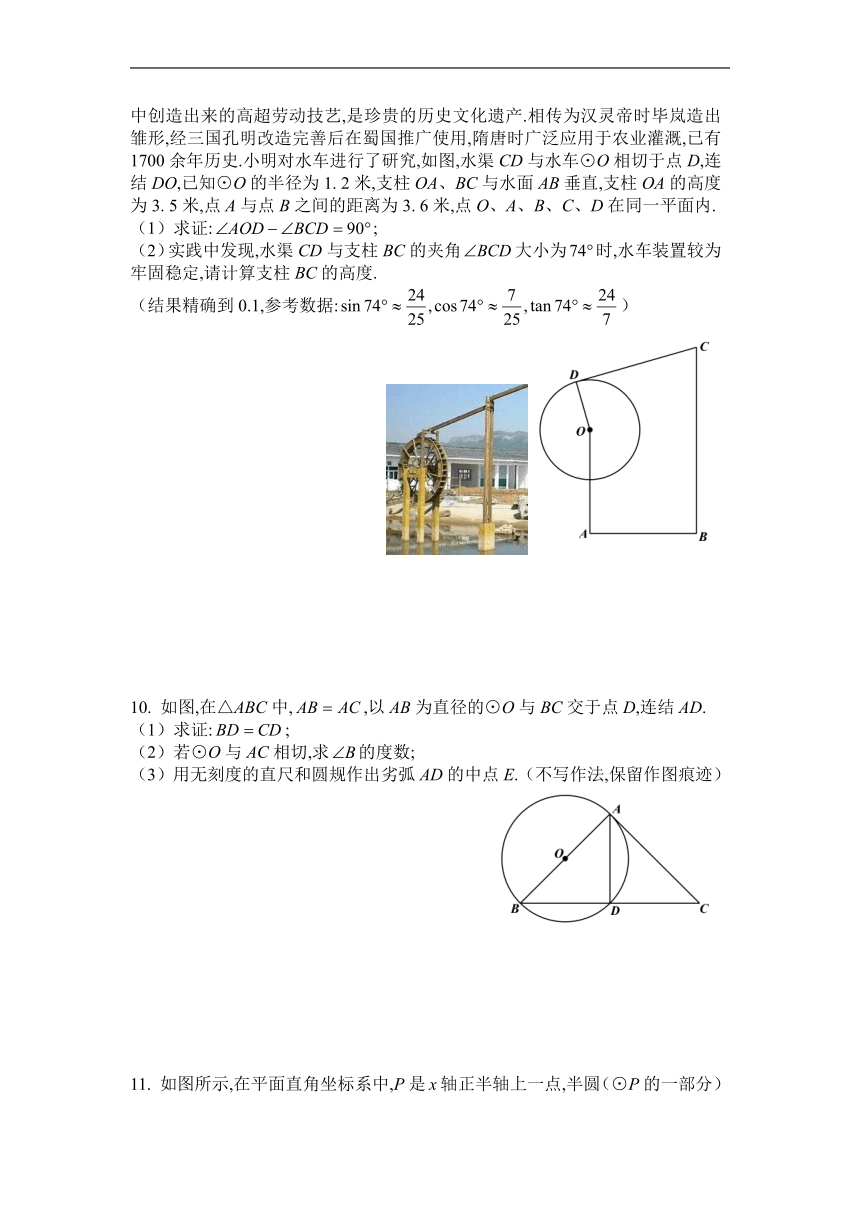
7. 如图1,中国古代的马车已经涉及很复杂的机械设计,包含大量零部件和工艺,所彰显的智慧让人叹服.如图2是马车的侧面示意图,AB为车轮⊙O的直径,过圆心O的车架AC一端点C着地时,地面CD与车轮⊙O相切于点D,连结AD、BD.
(1)求证:;
(2)若,则的度数是_________;
(3)若米,求车轮的半径长.
8. 如图,点O在△ABC的边AB上,⊙O与边AC相切于点E,与边BC、AB分别交于点D、F,且.
(1)求证:;
(2)当时,求⊙O的半径.
9. 水车又称孔明车,是中国最古老的农业灌溉工具,是先人们在征服世界的过程中创造出来的高超劳动技艺,是珍贵的历史文化遗产.相传为汉灵帝时毕岚造出雏形,经三国孔明改造完善后在蜀国推广使用,隋唐时广泛应用于农业灌溉,已有1700余年历史.小明对水车进行了研究,如图,水渠CD与水车⊙O相切于点D,连结DO,已知⊙O的半径为1. 2米,支柱OA、BC与水面AB垂直,支柱OA的高度为3. 5米,点A与点B之间的距离为3. 6米,点O、A、B、C、D在同一平面内.
(1)求证:;
(2)实践中发现,水渠CD与支柱BC的夹角大小为时,水车装置较为牢固稳定,请计算支柱BC的高度.
(结果精确到0.1,参考数据:)
10. 如图,在△ABC中,,以AB为直径的⊙O与BC交于点D,连结AD.
(1)求证:;
(2)若⊙O与AC相切,求的度数;
(3)用无刻度的直尺和圆规作出劣弧AD的中点E.(不写作法,保留作图痕迹)
11. 如图所示,在平面直角坐标系中,P是轴正半轴上一点,半圆(⊙P的一部分)与轴的正半轴交于A、B两点,A在B的左侧,且OA、OB的长是方程的两根.
(1)求⊙P的半径;
(2)过点O作半圆的切线,并证明所作直线为⊙P的切线;(要求尺规作图,保留作图痕迹)
(3)直接写出切点Q的坐标.
12.【材料】自从《义务教育数学课程标准(2022年版)》实施以来,九年级的晏老师通过查阅新课标获悉:切线长定理由“选学”改为“必学”,并新增“会过圆外的一个点作圆的切线”.在学习完《切线的性质与判定》后,她布置一题:已知,如图所示,⊙O及⊙O外一点P,求作:直线PQ,使PQ与⊙O相切于点Q.李蕾同学经过探索,给出了如下一种作图方法:
(1)连结OP,分别以O、P为圆心,以大于的长为半径画弧,两弧分别交于点A、B(A、B两点分别位于直线OP的上下侧);(2)作直线AB,AB交OP于点C;(3)以点C为圆心,CO为半径作⊙C,⊙C交⊙O于点Q(点Q位于直线OP的上侧);(4)连结PQ,PQ交AB于点D,则直线PQ即为所求.
【问题】(1)请按照步骤完成作图,并准确标注字母;
(2)结合图形,说明PQ是⊙O的切线;
(3)若⊙O的半径为2,,求QD的长.
中考圆的计算与证明最后一练解析版
1. 如图,MN是⊙O的直径,A、B是⊙O上的两点,过点A作⊙O的切线交BN的延长线于点C,,连结AB、AM.
(1)求证:;
(2)若⊙O的半径为,求线段AC的长.
(1)证明:∵AC与⊙O相切
∴
∴
∵
∴
∴
∴
∴
∵
∴;
(2)解:连结AN.
∵MN是⊙O的直径
∴
∵
∴
设
在Rt△AMN中,由勾股定理得:
∴
解之得:(舍去)
∴
∵
∴
∵
∴,∴△ACN∽△MAN
∴,∴.
2. 如图所示,以AE为直径的⊙O与△ABC的边BC相切于点D,,连结AD、DE.
(1)求证:AD平分;
(2)尺规作图:在⊙O上找一点F,使DF平分;(不写作法,保留作图痕迹)
(3)若(2)中DF与AB交于点G,,求线段FG的长.
(1)证明:连结OD.
∵BC与⊙O相切
∴
∴
∴
∴
∵
∴
∴
∴AD平分;
(2)解:如图所示;
(3)连结OF,作
∵AE是⊙O的直径
∴
∵DF平分
∴
∴
∴
∴
∴△FOG∽△DHG
在Rt△ABC中,由勾股定理得:
∵AD平分,
∴,则
∴
设,则
在Rt△BDH中,由勾股定理得:
∴,解之得:
∴
设⊙O的半径为,则
∵
∴△OBD∽△ABC
∴,解之得:∴
∴,
∵△FOG∽△DHG
∴
∴
在Rt△FOG中,由勾股定理得:
.
3. 如图所示,在Rt△ABC中,,点D在斜边BC上,直角边AC恰好与以BD为直径的半圆相切于点E,连结DE,过点O作,交AB于点F.
(1)请判断四边形BOEF的形状,并说明理由;
(2)若,求AB的长.
解:(1)四边形BOEF是菱形.
理由如下:∵AC与⊙O相切
∴
∴
∴
∴
∴
∵
∴
∵
∴
∴
∴
∵,
∴四边形BOEF是平行四边形
∵
∴四边形BOEF是菱形;
(2)由(1)可知:四边形BOEF是菱形
∴
∴
∴
设,在Rt△AEF中,由勾股定理得:
∴,解之得:
∴
∴.
4. 如图,BC是⊙O的直径,CE是⊙O的弦,过点E作⊙O的切线,交CB的延长线于点G,过点B作于点F,交CE的延长线于点A.
(1)求证:;
(2)若,⊙O的半径是2,求AF的长.
(1)证明:连结OE.
∵EG是⊙O的切线
∴
∴
∵
∴
∴
∴
∵
∴;
(2)解:在Rt△EOG中
∵
∴,
∴
∵
∴△GBF∽△GOE
∴,
∵
∴
∴
∴.
5. 如图,点C为线段AB的中点,BC为⊙O的直径,AD为⊙O的切线,切点为D.
(1)请用无刻度的直尺和圆规作,垂足为E,且直线OE交AD于点F;(要求:不写作法,保留作图痕迹,使用2B铅笔作图)
(2)在(1)的条件下:
①求证:;
②若,则EF的长为_________.
(1)解:如图所示;
点评: 根据本题题目条件,作图方法不唯一,如连结OD,则△COD是等腰三角形,作出的平分线即可;也可作出线段CD的垂直平分线,垂足为点E,连结OE即可;还可以分别以点C、D为圆心,以大于的长为半径在⊙O的外部画弧,两弧交于点G,连结OG,交CD于点E.
(2)①证明:连结OD.
∵AD为⊙O的切线
∴
∴
∵
∴
∴
∵
∴
∴;
② 2.
提示:∵BC是⊙O的直径
∴
∴
∵点O是BC的中点
∴
∵点C为线段AB的中点
∴,
∵()
∴△AOF∽△ABD
∴,
∴.
6. 如图,AB为⊙O的直径,C为⊙O上的一点,交AC于点E,.
(1)求证:DC是⊙O的切线;
(2)若求CD的长及.
(1)证明:∵
∴
∵
∴
∵
∴
∵
∴
∴
∴
∵OC是⊙O的半径
∴DC是⊙O的切线;
(2)解:设
∵
∴
在Rt△COD中,由勾股定理得:
∴,解之得:
∴,
在Rt△COD中,∵
∴.
7. 如图1,中国古代的马车已经涉及很复杂的机械设计,包含大量零部件和工艺,所彰显的智慧让人叹服.如图2是马车的侧面示意图,AB为车轮⊙O的直径,过圆心O的车架AC一端点C着地时,地面CD与车轮⊙O相切于点D,连结AD、BD.
(1)求证:;
(2)若,则的度数是_________;
(3)若米,求车轮的半径长.
(1)证明:连结OD.
∵CD与车轮⊙O相切
∴
∴
∵
∴
∴
∵AB为⊙O的直径
∴
∴
∴;
(2);
提示: 由(1)可知,
∴
∴;
(2)由(1)可知:
∵
∴△BCD∽△DCA
∴
∴米,米
∵AB为⊙O的直径
∴车轮的半径长为米
答:车轮的半径长为0.55米.
8. 如图,点O在△ABC的边AB上,⊙O与边AC相切于点E,与边BC、AB分别交于点D、F,且.
(1)求证:;
(2)当时,求⊙O的半径.
(1)证明:连结OE.
∵⊙O与边AC相切
∴
∴
∵
∴
∵
∴弧EF=弧ED(大家用弧的符号表示,这里由于软件的问题无法使用)
∴
∴
∴
∴;
(2)解:在Rt△ABC中,由勾股定理得:
设⊙O的半径为,则
∵
∴△AOE∽△ABC
∴,解之得:
∴⊙O的半径为.
9. 水车又称孔明车,是中国最古老的农业灌溉工具,是先人们在征服世界的过程中创造出来的高超劳动技艺,是珍贵的历史文化遗产.相传为汉灵帝时毕岚造出雏形,经三国孔明改造完善后在蜀国推广使用,隋唐时广泛应用于农业灌溉,已有1700余年历史.小明对水车进行了研究,如图,水渠CD与水车⊙O相切于点D,连结DO,已知⊙O的半径为1. 2米,支柱OA、BC与水面AB垂直,支柱OA的高度为3. 5米,点A与点B之间的距离为3. 6米,点O、A、B、C、D在同一平面内.
(1)求证:;
(2)实践中发现,水渠CD与支柱BC的夹角大小为时,水车装置较为牢固稳定,请计算支柱BC的高度.
(结果精确到0.1,参考数据:)
(1)证明:延长AO交CD于点E.
∵
∴
∴
∴
∵CD与⊙O相切
∴
∴
∵
∴;
(2)作于点F,则四边形ABFE为矩形
∴米,
在Rt△DOE中
∵
∴米
∴米
在Rt△EFC中
∵
∴米
∴米
答:支柱BC的高度约为5. 8米.
10. 如图,在△ABC中,,以AB为直径的⊙O与BC交于点D,连结AD.
(1)求证:;
(2)若⊙O与AC相切,求的度数;
(3)用无刻度的直尺和圆规作出劣弧AD的中点E.(不写作法,保留作图痕迹)
(1)证明:∵AB为⊙O的直径
∴
∴
∵,
∴;
(2)解:∵⊙O与AC相切
∴
∴
∵
∴△ABC是等腰直角三角形
∴;
(3)如图所示;
11. 如图所示,在平面直角坐标系中,P是轴正半轴上一点,半圆(⊙P的一部分)与轴的正半轴交于A、B两点,A在B的左侧,且OA、OB的长是方程的两根.
(1)求⊙P的半径;
(2)过点O作半圆的切线,并证明所作直线为⊙P的切线;(要求尺规作图,保留作图痕迹)
(3)直接写出切点Q的坐标.
解:(1)解方程得:
∴
∴
∴⊙P的半径为2;
(2)以点A为圆心,以AP的长为半径画弧,交⊙P与点Q,则OQ是⊙P的切线.
理由如下:由尺规作图可知:
∴,△APQ为等边三角形
∴
∵
∴
∴
∴
∴
∵PQ是⊙P的半径
∴OQ是⊙P的切线;
(3)
提示: 作轴.
12.【材料】自从《义务教育数学课程标准(2022年版)》实施以来,九年级的晏老师通过查阅新课标获悉:切线长定理由“选学”改为“必学”,并新增“会过圆外的一个点作圆的切线”.在学习完《切线的性质与判定》后,她布置一题:已知,如图所示,⊙O及⊙O外一点P,求作:直线PQ,使PQ与⊙O相切于点Q.李蕾同学经过探索,给出了如下一种作图方法:
(1)连结OP,分别以O、P为圆心,以大于的长为半径画弧,两弧分别交于点A、B(A、B两点分别位于直线OP的上下侧);(2)作直线AB,AB交OP于点C;(3)以点C为圆心,CO为半径作⊙C,⊙C交⊙O于点Q(点Q位于直线OP的上侧);(4)连结PQ,PQ交AB于点D,则直线PQ即为所求.
【问题】(1)请按照步骤完成作图,并准确标注字母;
(2)结合图形,说明PQ是⊙O的切线;
(3)若⊙O的半径为2,,求QD的长.
(1)解:(1)如图所示;
(2)证明:连结OQ.
∵OP为⊙C的直径
∴
∴
∵OQ为⊙O的半径
∴PQ是⊙O的切线;
(3)由尺规作图可知:AB垂直平分OP
∴
在Rt△POQ中,由勾股定理得:
∴
在Rt△PCD中
∵
∴
∴.
1. 如图,MN是⊙O的直径,A、B是⊙O上的两点,过点A作⊙O的切线交BN的延长线于点C,,连结AB、AM.
(1)求证:;
(2)若⊙O的半径为,求线段AC的长.
2. 如图所示,以AE为直径的⊙O与△ABC的边BC相切于点D,,连结AD、DE.
(1)求证:AD平分;
(2)尺规作图:在⊙O上找一点F,使DF平分;(不写作法,保留作图痕迹)
(3)若(2)中DF与AB交于点G,,求线段FG的长.
3. 如图所示,在Rt△ABC中,,点D在斜边BC上,直角边AC恰好与以BD为直径的半圆相切于点E,连结DE,过点O作,交AB于点F.
(1)请判断四边形BOEF的形状,并说明理由;
(2)若,求AB的长.
4. 如图,BC是⊙O的直径,CE是⊙O的弦,过点E作⊙O的切线,交CB的延长线于点G,过点B作于点F,交CE的延长线于点A.
(1)求证:;
(2)若,⊙O的半径是2,求AF的长.
5. 如图,点C为线段AB的中点,BC为⊙O的直径,AD为⊙O的切线,切点为D.
(1)请用无刻度的直尺和圆规作,垂足为E,且直线OE交AD于点F;(要求:不写作法,保留作图痕迹,使用2B铅笔作图)
(2)在(1)的条件下:
①求证:;
②若,则EF的长为_________.
6. 如图,AB为⊙O的直径,C为⊙O上的一点,交AC于点E,.
(1)求证:DC是⊙O的切线;
(2)若求CD的长及.
7. 如图1,中国古代的马车已经涉及很复杂的机械设计,包含大量零部件和工艺,所彰显的智慧让人叹服.如图2是马车的侧面示意图,AB为车轮⊙O的直径,过圆心O的车架AC一端点C着地时,地面CD与车轮⊙O相切于点D,连结AD、BD.
(1)求证:;
(2)若,则的度数是_________;
(3)若米,求车轮的半径长.
8. 如图,点O在△ABC的边AB上,⊙O与边AC相切于点E,与边BC、AB分别交于点D、F,且.
(1)求证:;
(2)当时,求⊙O的半径.
9. 水车又称孔明车,是中国最古老的农业灌溉工具,是先人们在征服世界的过程中创造出来的高超劳动技艺,是珍贵的历史文化遗产.相传为汉灵帝时毕岚造出雏形,经三国孔明改造完善后在蜀国推广使用,隋唐时广泛应用于农业灌溉,已有1700余年历史.小明对水车进行了研究,如图,水渠CD与水车⊙O相切于点D,连结DO,已知⊙O的半径为1. 2米,支柱OA、BC与水面AB垂直,支柱OA的高度为3. 5米,点A与点B之间的距离为3. 6米,点O、A、B、C、D在同一平面内.
(1)求证:;
(2)实践中发现,水渠CD与支柱BC的夹角大小为时,水车装置较为牢固稳定,请计算支柱BC的高度.
(结果精确到0.1,参考数据:)
10. 如图,在△ABC中,,以AB为直径的⊙O与BC交于点D,连结AD.
(1)求证:;
(2)若⊙O与AC相切,求的度数;
(3)用无刻度的直尺和圆规作出劣弧AD的中点E.(不写作法,保留作图痕迹)
11. 如图所示,在平面直角坐标系中,P是轴正半轴上一点,半圆(⊙P的一部分)与轴的正半轴交于A、B两点,A在B的左侧,且OA、OB的长是方程的两根.
(1)求⊙P的半径;
(2)过点O作半圆的切线,并证明所作直线为⊙P的切线;(要求尺规作图,保留作图痕迹)
(3)直接写出切点Q的坐标.
12.【材料】自从《义务教育数学课程标准(2022年版)》实施以来,九年级的晏老师通过查阅新课标获悉:切线长定理由“选学”改为“必学”,并新增“会过圆外的一个点作圆的切线”.在学习完《切线的性质与判定》后,她布置一题:已知,如图所示,⊙O及⊙O外一点P,求作:直线PQ,使PQ与⊙O相切于点Q.李蕾同学经过探索,给出了如下一种作图方法:
(1)连结OP,分别以O、P为圆心,以大于的长为半径画弧,两弧分别交于点A、B(A、B两点分别位于直线OP的上下侧);(2)作直线AB,AB交OP于点C;(3)以点C为圆心,CO为半径作⊙C,⊙C交⊙O于点Q(点Q位于直线OP的上侧);(4)连结PQ,PQ交AB于点D,则直线PQ即为所求.
【问题】(1)请按照步骤完成作图,并准确标注字母;
(2)结合图形,说明PQ是⊙O的切线;
(3)若⊙O的半径为2,,求QD的长.
中考圆的计算与证明最后一练解析版
1. 如图,MN是⊙O的直径,A、B是⊙O上的两点,过点A作⊙O的切线交BN的延长线于点C,,连结AB、AM.
(1)求证:;
(2)若⊙O的半径为,求线段AC的长.
(1)证明:∵AC与⊙O相切
∴
∴
∵
∴
∴
∴
∴
∵
∴;
(2)解:连结AN.
∵MN是⊙O的直径
∴
∵
∴
设
在Rt△AMN中,由勾股定理得:
∴
解之得:(舍去)
∴
∵
∴
∵
∴,∴△ACN∽△MAN
∴,∴.
2. 如图所示,以AE为直径的⊙O与△ABC的边BC相切于点D,,连结AD、DE.
(1)求证:AD平分;
(2)尺规作图:在⊙O上找一点F,使DF平分;(不写作法,保留作图痕迹)
(3)若(2)中DF与AB交于点G,,求线段FG的长.
(1)证明:连结OD.
∵BC与⊙O相切
∴
∴
∴
∴
∵
∴
∴
∴AD平分;
(2)解:如图所示;
(3)连结OF,作
∵AE是⊙O的直径
∴
∵DF平分
∴
∴
∴
∴
∴△FOG∽△DHG
在Rt△ABC中,由勾股定理得:
∵AD平分,
∴,则
∴
设,则
在Rt△BDH中,由勾股定理得:
∴,解之得:
∴
设⊙O的半径为,则
∵
∴△OBD∽△ABC
∴,解之得:∴
∴,
∵△FOG∽△DHG
∴
∴
在Rt△FOG中,由勾股定理得:
.
3. 如图所示,在Rt△ABC中,,点D在斜边BC上,直角边AC恰好与以BD为直径的半圆相切于点E,连结DE,过点O作,交AB于点F.
(1)请判断四边形BOEF的形状,并说明理由;
(2)若,求AB的长.
解:(1)四边形BOEF是菱形.
理由如下:∵AC与⊙O相切
∴
∴
∴
∴
∴
∵
∴
∵
∴
∴
∴
∵,
∴四边形BOEF是平行四边形
∵
∴四边形BOEF是菱形;
(2)由(1)可知:四边形BOEF是菱形
∴
∴
∴
设,在Rt△AEF中,由勾股定理得:
∴,解之得:
∴
∴.
4. 如图,BC是⊙O的直径,CE是⊙O的弦,过点E作⊙O的切线,交CB的延长线于点G,过点B作于点F,交CE的延长线于点A.
(1)求证:;
(2)若,⊙O的半径是2,求AF的长.
(1)证明:连结OE.
∵EG是⊙O的切线
∴
∴
∵
∴
∴
∴
∵
∴;
(2)解:在Rt△EOG中
∵
∴,
∴
∵
∴△GBF∽△GOE
∴,
∵
∴
∴
∴.
5. 如图,点C为线段AB的中点,BC为⊙O的直径,AD为⊙O的切线,切点为D.
(1)请用无刻度的直尺和圆规作,垂足为E,且直线OE交AD于点F;(要求:不写作法,保留作图痕迹,使用2B铅笔作图)
(2)在(1)的条件下:
①求证:;
②若,则EF的长为_________.
(1)解:如图所示;
点评: 根据本题题目条件,作图方法不唯一,如连结OD,则△COD是等腰三角形,作出的平分线即可;也可作出线段CD的垂直平分线,垂足为点E,连结OE即可;还可以分别以点C、D为圆心,以大于的长为半径在⊙O的外部画弧,两弧交于点G,连结OG,交CD于点E.
(2)①证明:连结OD.
∵AD为⊙O的切线
∴
∴
∵
∴
∴
∵
∴
∴;
② 2.
提示:∵BC是⊙O的直径
∴
∴
∵点O是BC的中点
∴
∵点C为线段AB的中点
∴,
∵()
∴△AOF∽△ABD
∴,
∴.
6. 如图,AB为⊙O的直径,C为⊙O上的一点,交AC于点E,.
(1)求证:DC是⊙O的切线;
(2)若求CD的长及.
(1)证明:∵
∴
∵
∴
∵
∴
∵
∴
∴
∴
∵OC是⊙O的半径
∴DC是⊙O的切线;
(2)解:设
∵
∴
在Rt△COD中,由勾股定理得:
∴,解之得:
∴,
在Rt△COD中,∵
∴.
7. 如图1,中国古代的马车已经涉及很复杂的机械设计,包含大量零部件和工艺,所彰显的智慧让人叹服.如图2是马车的侧面示意图,AB为车轮⊙O的直径,过圆心O的车架AC一端点C着地时,地面CD与车轮⊙O相切于点D,连结AD、BD.
(1)求证:;
(2)若,则的度数是_________;
(3)若米,求车轮的半径长.
(1)证明:连结OD.
∵CD与车轮⊙O相切
∴
∴
∵
∴
∴
∵AB为⊙O的直径
∴
∴
∴;
(2);
提示: 由(1)可知,
∴
∴;
(2)由(1)可知:
∵
∴△BCD∽△DCA
∴
∴米,米
∵AB为⊙O的直径
∴车轮的半径长为米
答:车轮的半径长为0.55米.
8. 如图,点O在△ABC的边AB上,⊙O与边AC相切于点E,与边BC、AB分别交于点D、F,且.
(1)求证:;
(2)当时,求⊙O的半径.
(1)证明:连结OE.
∵⊙O与边AC相切
∴
∴
∵
∴
∵
∴弧EF=弧ED(大家用弧的符号表示,这里由于软件的问题无法使用)
∴
∴
∴
∴;
(2)解:在Rt△ABC中,由勾股定理得:
设⊙O的半径为,则
∵
∴△AOE∽△ABC
∴,解之得:
∴⊙O的半径为.
9. 水车又称孔明车,是中国最古老的农业灌溉工具,是先人们在征服世界的过程中创造出来的高超劳动技艺,是珍贵的历史文化遗产.相传为汉灵帝时毕岚造出雏形,经三国孔明改造完善后在蜀国推广使用,隋唐时广泛应用于农业灌溉,已有1700余年历史.小明对水车进行了研究,如图,水渠CD与水车⊙O相切于点D,连结DO,已知⊙O的半径为1. 2米,支柱OA、BC与水面AB垂直,支柱OA的高度为3. 5米,点A与点B之间的距离为3. 6米,点O、A、B、C、D在同一平面内.
(1)求证:;
(2)实践中发现,水渠CD与支柱BC的夹角大小为时,水车装置较为牢固稳定,请计算支柱BC的高度.
(结果精确到0.1,参考数据:)
(1)证明:延长AO交CD于点E.
∵
∴
∴
∴
∵CD与⊙O相切
∴
∴
∵
∴;
(2)作于点F,则四边形ABFE为矩形
∴米,
在Rt△DOE中
∵
∴米
∴米
在Rt△EFC中
∵
∴米
∴米
答:支柱BC的高度约为5. 8米.
10. 如图,在△ABC中,,以AB为直径的⊙O与BC交于点D,连结AD.
(1)求证:;
(2)若⊙O与AC相切,求的度数;
(3)用无刻度的直尺和圆规作出劣弧AD的中点E.(不写作法,保留作图痕迹)
(1)证明:∵AB为⊙O的直径
∴
∴
∵,
∴;
(2)解:∵⊙O与AC相切
∴
∴
∵
∴△ABC是等腰直角三角形
∴;
(3)如图所示;
11. 如图所示,在平面直角坐标系中,P是轴正半轴上一点,半圆(⊙P的一部分)与轴的正半轴交于A、B两点,A在B的左侧,且OA、OB的长是方程的两根.
(1)求⊙P的半径;
(2)过点O作半圆的切线,并证明所作直线为⊙P的切线;(要求尺规作图,保留作图痕迹)
(3)直接写出切点Q的坐标.
解:(1)解方程得:
∴
∴
∴⊙P的半径为2;
(2)以点A为圆心,以AP的长为半径画弧,交⊙P与点Q,则OQ是⊙P的切线.
理由如下:由尺规作图可知:
∴,△APQ为等边三角形
∴
∵
∴
∴
∴
∴
∵PQ是⊙P的半径
∴OQ是⊙P的切线;
(3)
提示: 作轴.
12.【材料】自从《义务教育数学课程标准(2022年版)》实施以来,九年级的晏老师通过查阅新课标获悉:切线长定理由“选学”改为“必学”,并新增“会过圆外的一个点作圆的切线”.在学习完《切线的性质与判定》后,她布置一题:已知,如图所示,⊙O及⊙O外一点P,求作:直线PQ,使PQ与⊙O相切于点Q.李蕾同学经过探索,给出了如下一种作图方法:
(1)连结OP,分别以O、P为圆心,以大于的长为半径画弧,两弧分别交于点A、B(A、B两点分别位于直线OP的上下侧);(2)作直线AB,AB交OP于点C;(3)以点C为圆心,CO为半径作⊙C,⊙C交⊙O于点Q(点Q位于直线OP的上侧);(4)连结PQ,PQ交AB于点D,则直线PQ即为所求.
【问题】(1)请按照步骤完成作图,并准确标注字母;
(2)结合图形,说明PQ是⊙O的切线;
(3)若⊙O的半径为2,,求QD的长.
(1)解:(1)如图所示;
(2)证明:连结OQ.
∵OP为⊙C的直径
∴
∴
∵OQ为⊙O的半径
∴PQ是⊙O的切线;
(3)由尺规作图可知:AB垂直平分OP
∴
在Rt△POQ中,由勾股定理得:
∴
在Rt△PCD中
∵
∴
∴.
同课章节目录
