【考前必刷】浙江地区2023年中考数学全真模拟卷5(含解析)
文档属性
| 名称 | 【考前必刷】浙江地区2023年中考数学全真模拟卷5(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-03 22:21:09 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
【考前必刷】浙江地区中考数学全真模拟卷5
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.一个不透明的袋子里装有6个红球和4个黄球,它们除颜色外其余都相同.从袋中任意摸出一个球是红球的概率为( )
A. B. C. D.
2.我国古代数学名著《九章算术》中记载:“今有共买物,人出八,盈三;人出七,不足四.问人数、物价各几何?”大意是:现在有数人一起去买某物品,如果每人出8钱,则多了3钱;如果每人出7钱,则少了4钱.问共有多少人,物品的价格是多少钱?若设人数共有x人,物品的价格为y钱,可列方程组为( )
A. B. C. D.
3.某物体如图所示,它的主视图是( )
A. B. C. D.
4.新农村建设示范村“幸福村”为配合上级部门做好春耕防汛工作,进一步推进美丽乡村建设,计划重修一条标准化示范水渠(如图),水渠的横截面是一个等腰梯形.根据工程造价预算,水渠的湿周(即图中的的长)为10米,当汛情来临时,为使得水渠的泄洪量达到最大,水渠横截面的底边长BC应设计成( )米
A.5 B. C. D.
5.从一块半径是4m的圆形铁片上剪出一个圆心角为的扇形,将剪下的扇形围成一个圆锥,圆锥的高是( )
A. B.2m C.4m D.
6.如图1,点是半圆上一个动点,点从点开始向终点运动的整个过程中,的弧长与时间(秒)的函数关系如图2所示,则点运动至秒时,的度数为( )
A. B. C. D.
7.一组数据:7,5,8,7,9.这组数据的众数是( )
A.5 B.7 C.8 D.9
8.的相反数是( )
A.2 B. C. D.
9.如果,下列各式中不正确的是( )
A. B. C. D.
10.2023年杭州亚运会将于2023年9月23日开幕.赛会志愿者招募数据显示,杭州亚运会赛会志愿者注册总人数万,其中万用科学记数法表示为( )
A. B. C. D.
二、解答题
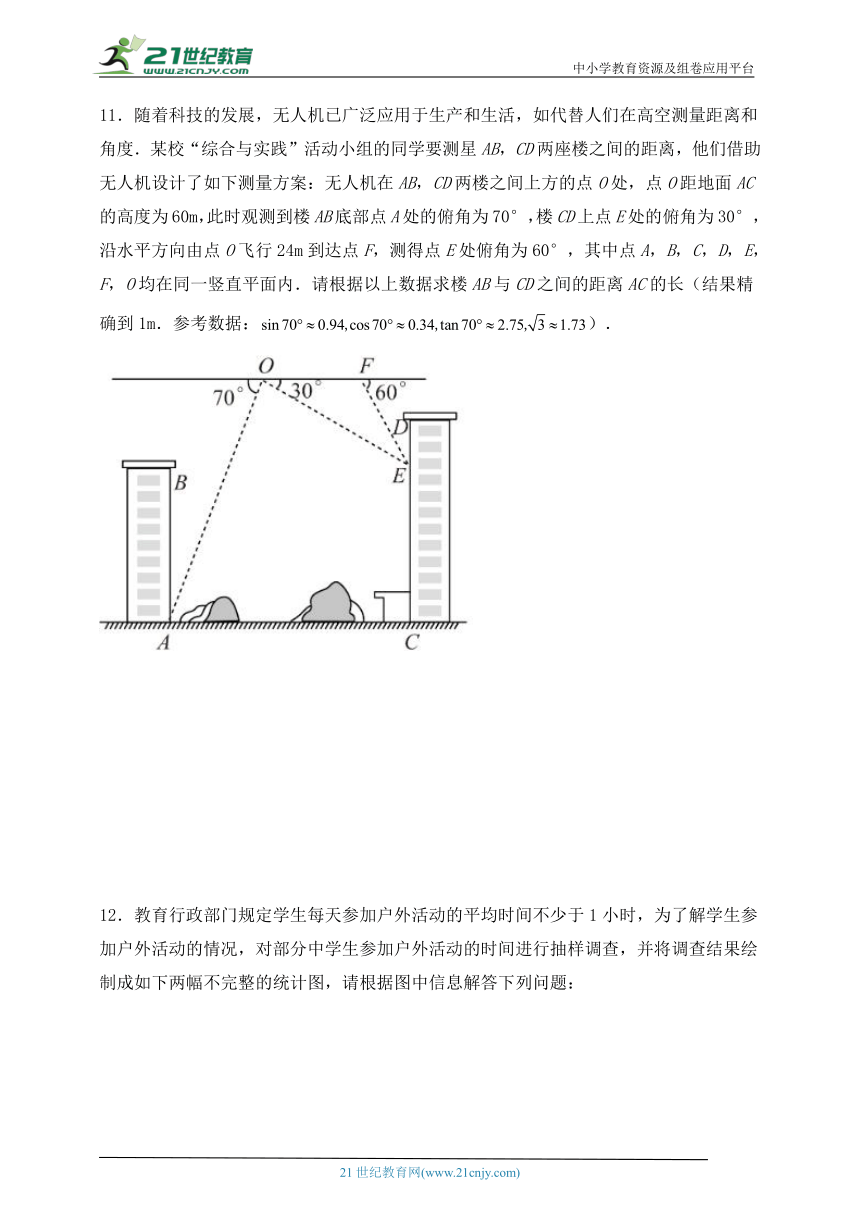
11.随着科技的发展,无人机已广泛应用于生产和生活,如代替人们在高空测量距离和角度.某校“综合与实践”活动小组的同学要测星AB,CD两座楼之间的距离,他们借助无人机设计了如下测量方案:无人机在AB,CD两楼之间上方的点O处,点O距地面AC的高度为60m,此时观测到楼AB底部点A处的俯角为70°,楼CD上点E处的俯角为30°,沿水平方向由点O飞行24m到达点F,测得点E处俯角为60°,其中点A,B,C,D,E,F,O均在同一竖直平面内.请根据以上数据求楼AB与CD之间的距离AC的长(结果精确到1m.参考数据:).
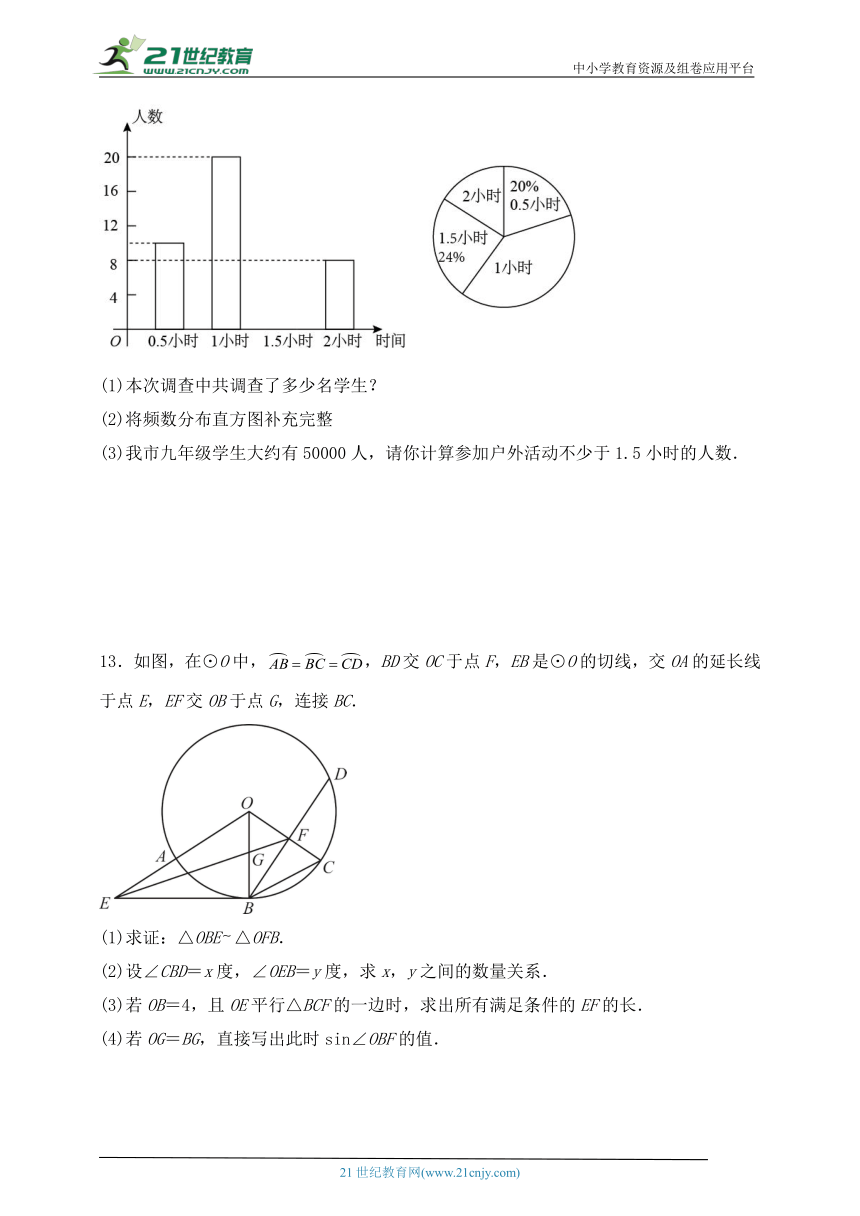
12.教育行政部门规定学生每天参加户外活动的平均时间不少于1小时,为了解学生参加户外活动的情况,对部分中学生参加户外活动的时间进行抽样调查,并将调查结果绘制成如下两幅不完整的统计图,请根据图中信息解答下列问题:
(1)本次调查中共调查了多少名学生?
(2)将频数分布直方图补充完整
(3)我市九年级学生大约有50000人,请你计算参加户外活动不少于1.5小时的人数.
13.如图,在⊙O中,,BD交OC于点F,EB是⊙O的切线,交OA的延长线于点E,EF交OB于点G,连接BC.
(1)求证:△OBE△OFB.
(2)设∠CBD=x度,∠OEB=y度,求x,y之间的数量关系.
(3)若OB=4,且OE平行△BCF的一边时,求出所有满足条件的EF的长.
(4)若OG=BG,直接写出此时sin∠OBF的值.
14.如图,在小正三角形组成的网格ABCD中,每个小正三角形的顶点叫做格点,各顶点在格点处的多边形称为格点多边形,按要求在网格中作一个格点多边形.
(1)请在图1中画一个矩形EFGH,使点E,F,G,H分别落在边AB,BC,CD,AD上.
(2)请在图2中画一个菱形MNPQ,使点M,N,P,Q分别落在边AB,BC,CD,AD上.
15.如图,CD为⊙O上两点,且在直径AB的两侧,CD交AB于点E,∠ABC=∠CAD,连接CO.
(1)求证:∠CAB=∠CDO.
(2)若AB=10,,求AD的长.
16.如图,直角坐标系中,抛物线y=ax2﹣(b﹣2)x+3a+8(a<0,a,b均为常数)经过点(1,8),分别交y轴正半轴于点C,交x轴于点M,N,顶点为点D,P为线段OC上一动点,过点P作x轴的平行线分别交抛物线于点A,B(点A在点B的左边).
(1)用含a的代数式表示b.
(2)求该抛物线的对称轴及PB﹣AP的值.
(3)当OP=4CP时,点D关于AB的对称点Q的纵坐标为﹣1,求此时MN的长.
17.某兴趣小组针对视力情况随机抽取本校部分学生进行调查,将调查结果进行统计分析,绘制成如下不完整的统计图表.
抽取的学生视力情况统计表
类别 调查结果 人数
A 正常 48
B 轻度近视 76
C 中度近视 60
D 重度近视 m
请根据图表信息解答下列问题:
(1)填空:m= _________,n= _________;
(2)该校共有学生1600人,请估算该校学生中“中度近视”的人数;
(3)某班有四名重度近视的学生甲、乙、丙、丁,从中随机选择两名学生参加学校组织的“爱眼护眼”座谈会,请用列表或画树状图的方法求同时选中甲和乙的概率.
三、填空题
18.如图,将含有的绕顶点顺时针旋转得到,点经过的路径为弧.若DE∥AB,,则图中阴影部分的面积是_________.
19.如图,在四边形中,,平分,点是的中点.
(1)已知,若,则的长度为__________;
(2)度数的最大值为_________.
20.已知△ABC中,∠BAC=90°,∠B=30°.用尺规画出射线AP(痕迹如图),则∠APB的度数为_____.
21.如图,将矩形纸片ABCD的四个角向内折叠,EH,EF,FG ,GH别为折痕, 其中点A,B落在点J处,点C,D落在点K处,且点H,J,K,F在同一直线上.
(1)四边形EFGH 的形状为____________.
(2)若,JK=,则AB=__________.
22.已知一组数据 , , , , 的平均数是3,方差是 ,那么另一组数据 , , , , 的平均数是_____,方差是_____.
23.图,方格纸中2个小正方形的边长均为1,图中阴影部分均为扇形,则这两个小扇形的面积之和为______(结果保留).
参考答案:
1.B
【分析】从袋中任意摸出一个球共有10种等可能结果,其中是红球的有6种结果,再根据概率公式求解即可.
【详解】解:从袋中任意摸出一个球共有10种等可能结果,其中是红球的有6种结果,
所以从袋中任意摸出一个球是红球的概率为.
故选:B.
【点睛】本题主要考查了概率公式,熟练掌握概率公式进行求解是解决本题的关键.
2.D
【分析】设有x人,物品的价格为y钱,根据所花总钱数不变列出方程即可.
【详解】设有x人,物品的价格为y钱,
根据题意,可列方程:,
故选:D.
【点睛】本题考查了由实际问题抽象出二元一次方程的应用,解答本题的关键是读懂题意,设出未知数,找出合适的等量关系.
3.A
【分析】根据立体图形的主视图是从正面看物体得到的平面图形即可解答.
【详解】解:∵立体几何的主视图一个圆和一个平行四边形,
故选.
【点睛】本题考查了立体图形的主视图是从正面看物体得到的平面图形,熟记主视图的定义是解题的关键.
4.B
【分析】过点D作交的延长线于点H,设,结合图形得到,利用梯形面积公式得到截面,利用二次函数的性质求解即可.
【详解】解:设底边长,则,
过点D作交的延长线于点H,又,
,,
,
,
,
故当时,最大,水渠的泄洪量达到最大,即.
故选:B
【点睛】本题主要考查二次函数的应用,理解题意,结合图形正确的求得二次函数解析式,并熟练运用二次函数的性质是解题的关键.
5.D
【详解】设圆锥的底面圆的半径为r,利用圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长和弧长公式,得到,解得,然后利用勾股定理计算圆锥的高.
【分析】解:设圆锥的底面圆的半径为r,
根据题意得,解得
所以圆锥的高.
故选:D.
【点睛】此题主要考查了圆锥的计算,勾股定理,解答此题的关键是求出扇形围成的圆锥的底面半径是多少.
6.C
【分析】根据图像可知半圆的周长为进而得到半圆的半径为,再根据题意得到弧长与时间(秒)的函数关系式及弧长公式即可解答.
【详解】解:设半圆的半径为,,
根据图像可知半圆的周长为,
∴,
∴,
设弧长与时间(秒)的函数关系式:,
∵图像经过,
∴,
∴弧长与时间(秒)的函数关系式为,
∴当秒时,,
∴根据弧长公式可知:,
∴,
故选.
【点睛】本题考查了一次函数与几何图形关系,弧长公式,一次函数图像与性质,掌握一次函数与几何图形关系是解题的关键.
7.B
【分析】根据众数的定义求解即可.
【详解】这组数据中7出现2次,次数最多
所以这组数据的众数为7
故选:B.
【点睛】本题主要考查众数,一组数据中出现次数最多的数据叫做众数.
8.A
【分析】根据相反数的定义“只有符号不相同的两个数互为相反数”即可得答案.
【详解】解:的相反数是2.
故选:A.
【点睛】本题考查了相反数的定义,熟记相反数的定义是解题关键.
9.B
【分析】利用不等式的性质对每个选项进行逐一判断即可得出结论.
【详解】解:,
由不等式的性质,不等式的两边同减去3,不等号的方向不变,
,
又
A选项的结论正确,不符合题意;
若,由不等式的性质,不等式的两边同乘,不等号的方向不变,
,
若,则,
B选项的结论不正确,符合题意;
,
,
C选项的结论正确,不符合题意;
,
,
D选项的结论正确,不符合题意.
故选:B.
【点睛】本题主要考查了不等式的性质,熟练掌握不等式的性质是解题的关键.
10.D
【分析】用科学记数法表示较大的数时,一般形式为,其中,n为整数
【详解】解:万用科学记数法表示为.
故选:D.
【点睛】本题考查了科学记数法,科学记数法的表示形式为的形式,其中,n为整数.确定n的值时,要看把原来的数,变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值时,n是正数;当原数的绝对值时,n是负数,确定a与n的值是解题的关键.
11.58m
【分析】延长AB和CD分别与直线OF交于点G和点H,则,再根据图形应用三角函数即可求解.
【详解】解:延长AB和CD分别与直线OF交于点G和点H,则.
又∵,
∴四边形ACHG是矩形.
∴.
由题意,得.
在中,,
∴(m)﹒
∵是的外角,
∴.
∴.
∴m.
在中,
∴(m).
∴.
答:楼AB与CD之间的距离AC的长约为58m.
【点睛】本题主要考查三角函数的综合应用,正确构造直角三角形并应用三角函数进行求解是解题的关键.
12.(1)50人
(2)见解析
(3)20000人
【分析】(1)根据统计图找出活动时间为0.5小时的人数和百分比,计算得到答案;
(2)求出户外活动时间为1.5小时的人数,补充频数分布直方图;
(3)利用总人数乘以不少于1.5小时的人数的百分比即可得到答案.
(1)
解:调查的总人数是(人).
(2)
实践1.5小时的人数是(人),
补全图形如下:
(3)
参加户外活动不少于1.5小时的人数是(人).
【点睛】本题考查读频数分布直方图的能力和利用统计图获取信息的能力;利用样本估计总体,利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.
13.(1)见解析
(2)
(3),
(4)
【分析】(1)根据两角对应相等即可证明△OBE∽△OFB;
(2)根据角之间的关系即可求解;
(3)分OE∥BC和OE∥BF两种情况,分别求解即可;
(4)作EP∥OC交OB的延长线于点P,则OG=GB=GF,∠BOC=∠P=∠EOP,OB=BP,可得,设OG=GB=GF=1,则EG=3,,,.
【详解】(1)证明:∵,
∴,
∵是的切线,
∴,
∴.
(2)解:∵,
∴,
∵,
∴,
∴,
∴,即.
(3)解:①如图1,当时,,
∴是等边三角形,,,,
作的延长线于点H,,,,
在中,;
②如图2,当时,
∵,
∴,
∴,
在中,.
(4)解:如图3,作交的延长线于点P,
易知,,
不妨设,
则,,,
.
【点睛】本题考查了相似三角形的判定与性质,切线的性质,勾股定理,三角函数的定义等知识,熟练掌握这些知识点并会应用是解决问题的关键.
14.(1)见解析
(2)见解析
【分析】(1)根据轴对称与中心对称的性质即可求解;
(2)根据等边三角形的性质,以及菱形的性质,画出其中一个图形即可.
(1)
解:四边形是菱形,
根据轴对称的性质找在菱形的边上找到对称的两点,进而根据对角相等的且互相平分的四边形是矩形,画图如下,画出其中一个图形即可.
(2)
如图,根据菱形的判定,对角线互相垂直,画出其中一个图形即可.
【点睛】本题考查了中心对称与轴对称,等边三角形的性质,菱形的性质,矩形的性质,综合运用以上知识是解题的关键.
15.(1)见解析
(2)
【分析】(1)根据圆周角定理得到∠ADC=∠ABC,进而推出∠ADC=∠CAD,根据等腰三角形的性质得到∠OAD=∠ODA,根据角的和差即可得解;
(2)连接CO,并延长交AD于点F,利用SSS证明△AOC≌△DOC,则∠ACF=∠DCF,根据等腰三角形三线合一的性质得出CF⊥AD,AD=2AF,根据勾股定理得到BC=,解直角三角形得到AF=3,据此即可得解.
【详解】(1)证明:∵,,
∴,
∵,
∴,
∴.
(2)连接,并延长交于点F,
∵,
∴,
在中,,
∴△AOC≌△DOC(SSS),
∴∠ACF=∠DCF,
∴,,
∵是的直径,
∴,
∴
在中,,
∴.
【点睛】此题考查了全等三角形的判定与性质、圆周角定理,熟练掌握全等三角形的判定与性质是解题的关键.
16.(1)
(2),
(3)
【分析】(1)把点(1,8)代入抛物线解析式即可;
(2)根据抛物线对称轴的公式可求得对称轴,根据抛物线的对称性可得结论;
(3)根据抛物线解析式可求得OC的长及顶点D的坐标,再根据OP=4CP可求得OP的长,再由点关于直线对称列出方程,求解得出a的值,进而求出点M和点N的坐标,即可求出MN的长.
【详解】(1)把点代入抛物线得:,
整理得:;
(2)该抛物线的对称轴为直线,
过顶点D作轴于点E,交于点H,
∵轴,由对称性可知,,
∴.
(3)易知点,则,
∵,
∴,
又,
∴点,
∵点D关于的对称点的纵坐标为,
∴,
解得:,
此时,抛物线解析式为,
令,
解得:或x=5,
∴点M,N坐标分别为,
∴.
【点睛】本题主要考查抛物线的对称轴公式,顶点坐标,抛物线的对称性等内容,属于二次函数综合题,中等难度,解题关键是掌握相关性质定理.
17.(1)200,108
(2)估计该校学生中“中度近视”的人数约为480人;
(3)甲和乙两名学生同时被选中的概率为.
【分析】(1)从所取样本中根据“正常”的人数和所占比例求出所抽取的学生总人数;根据“中度近视”的人数求出所占比例,乘以360°即可求解;
(2)由全校共有学生人数乘以“中度近视”人数所占的比例即可;
(3)画树状图列出所有等可能结果,再利用概率公式计算可得.
【详解】(1)解:所抽取的学生总数为m=48÷24%=200(人),
n= 360×=108,
故答案为:200,108;
(2)解:1600×=480(人),
即估计该校学生中“中度近视”的人数约为480人;
(3)解:画树状图为:
共有12种等可能的结果数,其中甲和乙两名学生同时被选中的结果数为2,
所以甲和乙两名学生同时被选中的概率为=.
【点睛】本题考查扇形统计图、统计表以及用样本估计总体以及列表法与树状图法等知识;利用列表法或树状图法展示所有等可能的结果n,再从中选出符合事件A或B的结果数目m,然后利用概率公式计算事件A或事件B的概率.
18.
【分析】,根据旋转的性质可得△ABC≌△DBE,所以,用扇形面积公式计算即可.
【详解】解:由题意可得:∠CAB=30°,根据旋转的性质可得:∠BDE=∠CAB=30°,△ABC≌△DBE;
∵DEAB
∴∠BDE=∠ABD=30°
∵
∴
故答案为:.
【点睛】本题考查了阴影部分面积的计算、旋转的性质、平行的性质、扇形面积公式等知识,解题的关键是把不规则阴影部分的面积转化为规则图形的面积.
19.
【分析】(1)连接BD,分别解和,得到,进而利用勾股定理即可求解;
(2)由,,得到ABDO,即可得出度数的最大值.
【详解】解:(1)连接BD,
∵,,
∴,
∵点是的中点,,
∴,
,
,
∴,
∵平分,
∴,
∵,
∴,
∴,
,
∴.
故答案为:.
(2)由(1)可知,
又∵,
∴ABDO,
∴,
又∵,
∴,
∴,
∵,
∴当时,有最大值,
∴的最大值为:.
故答案为:.
【点睛】本题考查解直角三角形.添加适当辅助线是本题解题的关键.
20.105°/105度
【分析】根据AP为∠BAC的角平分线,先求出∠BAP的度数,再通过三角形内角和为180°,求出∠APB的度数即可.
【详解】解:通过图中作图痕迹可知AP为∠BAC的角平分线,
,
在△ABP中,,
故答案为:105°.
【点睛】本题考查了尺规作图画角平分线,三角形内角和定理等,能够通过图中作图痕迹得到AP为∠BAC的角平分线是解题的关键.
21. 矩形; .
【分析】(1)由题意,由折叠的性质得到,,则得到,同理可求,即可得到结论成立;
(2)设,,则求出,得到AH和DH的长度,然后证明,从而求出HF的长度,过点H作HI⊥BC于点I,则HI=AB,BI=AH,求出FI的长度,再利用勾股定理,即可求出答案.
【详解】解:(1)根据题意,由折叠的性质,
,,
∴,
即,
同理可求:,,
∴四边形EFGH是矩形;
故答案为:矩形;
(2)∵,
设,,
由折叠的性质,则AH=HJ,HD=HK,
∵,
∴,解得:,
∴,;
由(1)可知,四边形EFGH是矩形,
∴EF=HG,EF∥HG,
∴∠EFJ=∠GHK,
∵∠EJF=∠GKH=90°,
∴△EFJ≌△GHK,
∴FJ=HK,
∵HD=HK,FB=FJ,
∴HD=HK=FB=FJ=;
∴,
如图,过点H作HI⊥BC于点I,则HI=AB,BI=AH,
∴,
在直角中,由勾股定理则
;
∴;
故答案为:.
【点睛】本题考查了折叠的性质,矩形的判定和性质,全等三角形的判定和性质,勾股定理,解题的的关键是熟练掌握所学的知识,正确的分析题意.
22. 10 /4.5
【分析】根据方差和平均数的变化规律可得:数据3x1+1、3x2+1、3x3+1、3x4+1、3x5+1的平均数是3×3+1,方差是方差为(3×)2,再进行计算即可.
【详解】解:∵数据x1、x2、x3、x4、x5的平均数是3,方差为,
∴新数据3x1+1、3x2+1、3x3+1、3x4+1、3x5+1的平均数是3×3+1=10,
方差为,
故答案为:10,.
【点睛】此题考查了方差的特点,若在原来数据前乘以同一个数,平均数也乘以同一个数,而方差要乘以这个数的平方,若数据都加上一个数(或减去一个数)时,方差不变,即数据的波动情况不变.
23./
【分析】根据题意可得这两个扇形可组合成一个大扇形,且这两个扇形的的圆心角的和为90°,再根据扇形的面积公式,即可求解.
【详解】解:根据题意得:两个扇形的半径相等均为1,
∴这两个扇形可组合成一个大扇形,
∵这两个扇形的的圆心角正好是直角三角形的两个锐角,
∴这两个扇形的的圆心角的和为90°,
∴这两个小扇形的面积之和为.
故答案为:
【点睛】本题主要考查了学生的观察能力及计算能力.理解求不规则的图形的面积,可以转化为几个规则图形的面积的和或差来求是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
【考前必刷】浙江地区中考数学全真模拟卷5
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.一个不透明的袋子里装有6个红球和4个黄球,它们除颜色外其余都相同.从袋中任意摸出一个球是红球的概率为( )
A. B. C. D.
2.我国古代数学名著《九章算术》中记载:“今有共买物,人出八,盈三;人出七,不足四.问人数、物价各几何?”大意是:现在有数人一起去买某物品,如果每人出8钱,则多了3钱;如果每人出7钱,则少了4钱.问共有多少人,物品的价格是多少钱?若设人数共有x人,物品的价格为y钱,可列方程组为( )
A. B. C. D.
3.某物体如图所示,它的主视图是( )
A. B. C. D.
4.新农村建设示范村“幸福村”为配合上级部门做好春耕防汛工作,进一步推进美丽乡村建设,计划重修一条标准化示范水渠(如图),水渠的横截面是一个等腰梯形.根据工程造价预算,水渠的湿周(即图中的的长)为10米,当汛情来临时,为使得水渠的泄洪量达到最大,水渠横截面的底边长BC应设计成( )米
A.5 B. C. D.
5.从一块半径是4m的圆形铁片上剪出一个圆心角为的扇形,将剪下的扇形围成一个圆锥,圆锥的高是( )
A. B.2m C.4m D.
6.如图1,点是半圆上一个动点,点从点开始向终点运动的整个过程中,的弧长与时间(秒)的函数关系如图2所示,则点运动至秒时,的度数为( )
A. B. C. D.
7.一组数据:7,5,8,7,9.这组数据的众数是( )
A.5 B.7 C.8 D.9
8.的相反数是( )
A.2 B. C. D.
9.如果,下列各式中不正确的是( )
A. B. C. D.
10.2023年杭州亚运会将于2023年9月23日开幕.赛会志愿者招募数据显示,杭州亚运会赛会志愿者注册总人数万,其中万用科学记数法表示为( )
A. B. C. D.
二、解答题
11.随着科技的发展,无人机已广泛应用于生产和生活,如代替人们在高空测量距离和角度.某校“综合与实践”活动小组的同学要测星AB,CD两座楼之间的距离,他们借助无人机设计了如下测量方案:无人机在AB,CD两楼之间上方的点O处,点O距地面AC的高度为60m,此时观测到楼AB底部点A处的俯角为70°,楼CD上点E处的俯角为30°,沿水平方向由点O飞行24m到达点F,测得点E处俯角为60°,其中点A,B,C,D,E,F,O均在同一竖直平面内.请根据以上数据求楼AB与CD之间的距离AC的长(结果精确到1m.参考数据:).
12.教育行政部门规定学生每天参加户外活动的平均时间不少于1小时,为了解学生参加户外活动的情况,对部分中学生参加户外活动的时间进行抽样调查,并将调查结果绘制成如下两幅不完整的统计图,请根据图中信息解答下列问题:
(1)本次调查中共调查了多少名学生?
(2)将频数分布直方图补充完整
(3)我市九年级学生大约有50000人,请你计算参加户外活动不少于1.5小时的人数.
13.如图,在⊙O中,,BD交OC于点F,EB是⊙O的切线,交OA的延长线于点E,EF交OB于点G,连接BC.
(1)求证:△OBE△OFB.
(2)设∠CBD=x度,∠OEB=y度,求x,y之间的数量关系.
(3)若OB=4,且OE平行△BCF的一边时,求出所有满足条件的EF的长.
(4)若OG=BG,直接写出此时sin∠OBF的值.
14.如图,在小正三角形组成的网格ABCD中,每个小正三角形的顶点叫做格点,各顶点在格点处的多边形称为格点多边形,按要求在网格中作一个格点多边形.
(1)请在图1中画一个矩形EFGH,使点E,F,G,H分别落在边AB,BC,CD,AD上.
(2)请在图2中画一个菱形MNPQ,使点M,N,P,Q分别落在边AB,BC,CD,AD上.
15.如图,CD为⊙O上两点,且在直径AB的两侧,CD交AB于点E,∠ABC=∠CAD,连接CO.
(1)求证:∠CAB=∠CDO.
(2)若AB=10,,求AD的长.
16.如图,直角坐标系中,抛物线y=ax2﹣(b﹣2)x+3a+8(a<0,a,b均为常数)经过点(1,8),分别交y轴正半轴于点C,交x轴于点M,N,顶点为点D,P为线段OC上一动点,过点P作x轴的平行线分别交抛物线于点A,B(点A在点B的左边).
(1)用含a的代数式表示b.
(2)求该抛物线的对称轴及PB﹣AP的值.
(3)当OP=4CP时,点D关于AB的对称点Q的纵坐标为﹣1,求此时MN的长.
17.某兴趣小组针对视力情况随机抽取本校部分学生进行调查,将调查结果进行统计分析,绘制成如下不完整的统计图表.
抽取的学生视力情况统计表
类别 调查结果 人数
A 正常 48
B 轻度近视 76
C 中度近视 60
D 重度近视 m
请根据图表信息解答下列问题:
(1)填空:m= _________,n= _________;
(2)该校共有学生1600人,请估算该校学生中“中度近视”的人数;
(3)某班有四名重度近视的学生甲、乙、丙、丁,从中随机选择两名学生参加学校组织的“爱眼护眼”座谈会,请用列表或画树状图的方法求同时选中甲和乙的概率.
三、填空题
18.如图,将含有的绕顶点顺时针旋转得到,点经过的路径为弧.若DE∥AB,,则图中阴影部分的面积是_________.
19.如图,在四边形中,,平分,点是的中点.
(1)已知,若,则的长度为__________;
(2)度数的最大值为_________.
20.已知△ABC中,∠BAC=90°,∠B=30°.用尺规画出射线AP(痕迹如图),则∠APB的度数为_____.
21.如图,将矩形纸片ABCD的四个角向内折叠,EH,EF,FG ,GH别为折痕, 其中点A,B落在点J处,点C,D落在点K处,且点H,J,K,F在同一直线上.
(1)四边形EFGH 的形状为____________.
(2)若,JK=,则AB=__________.
22.已知一组数据 , , , , 的平均数是3,方差是 ,那么另一组数据 , , , , 的平均数是_____,方差是_____.
23.图,方格纸中2个小正方形的边长均为1,图中阴影部分均为扇形,则这两个小扇形的面积之和为______(结果保留).
参考答案:
1.B
【分析】从袋中任意摸出一个球共有10种等可能结果,其中是红球的有6种结果,再根据概率公式求解即可.
【详解】解:从袋中任意摸出一个球共有10种等可能结果,其中是红球的有6种结果,
所以从袋中任意摸出一个球是红球的概率为.
故选:B.
【点睛】本题主要考查了概率公式,熟练掌握概率公式进行求解是解决本题的关键.
2.D
【分析】设有x人,物品的价格为y钱,根据所花总钱数不变列出方程即可.
【详解】设有x人,物品的价格为y钱,
根据题意,可列方程:,
故选:D.
【点睛】本题考查了由实际问题抽象出二元一次方程的应用,解答本题的关键是读懂题意,设出未知数,找出合适的等量关系.
3.A
【分析】根据立体图形的主视图是从正面看物体得到的平面图形即可解答.
【详解】解:∵立体几何的主视图一个圆和一个平行四边形,
故选.
【点睛】本题考查了立体图形的主视图是从正面看物体得到的平面图形,熟记主视图的定义是解题的关键.
4.B
【分析】过点D作交的延长线于点H,设,结合图形得到,利用梯形面积公式得到截面,利用二次函数的性质求解即可.
【详解】解:设底边长,则,
过点D作交的延长线于点H,又,
,,
,
,
,
故当时,最大,水渠的泄洪量达到最大,即.
故选:B
【点睛】本题主要考查二次函数的应用,理解题意,结合图形正确的求得二次函数解析式,并熟练运用二次函数的性质是解题的关键.
5.D
【详解】设圆锥的底面圆的半径为r,利用圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长和弧长公式,得到,解得,然后利用勾股定理计算圆锥的高.
【分析】解:设圆锥的底面圆的半径为r,
根据题意得,解得
所以圆锥的高.
故选:D.
【点睛】此题主要考查了圆锥的计算,勾股定理,解答此题的关键是求出扇形围成的圆锥的底面半径是多少.
6.C
【分析】根据图像可知半圆的周长为进而得到半圆的半径为,再根据题意得到弧长与时间(秒)的函数关系式及弧长公式即可解答.
【详解】解:设半圆的半径为,,
根据图像可知半圆的周长为,
∴,
∴,
设弧长与时间(秒)的函数关系式:,
∵图像经过,
∴,
∴弧长与时间(秒)的函数关系式为,
∴当秒时,,
∴根据弧长公式可知:,
∴,
故选.
【点睛】本题考查了一次函数与几何图形关系,弧长公式,一次函数图像与性质,掌握一次函数与几何图形关系是解题的关键.
7.B
【分析】根据众数的定义求解即可.
【详解】这组数据中7出现2次,次数最多
所以这组数据的众数为7
故选:B.
【点睛】本题主要考查众数,一组数据中出现次数最多的数据叫做众数.
8.A
【分析】根据相反数的定义“只有符号不相同的两个数互为相反数”即可得答案.
【详解】解:的相反数是2.
故选:A.
【点睛】本题考查了相反数的定义,熟记相反数的定义是解题关键.
9.B
【分析】利用不等式的性质对每个选项进行逐一判断即可得出结论.
【详解】解:,
由不等式的性质,不等式的两边同减去3,不等号的方向不变,
,
又
A选项的结论正确,不符合题意;
若,由不等式的性质,不等式的两边同乘,不等号的方向不变,
,
若,则,
B选项的结论不正确,符合题意;
,
,
C选项的结论正确,不符合题意;
,
,
D选项的结论正确,不符合题意.
故选:B.
【点睛】本题主要考查了不等式的性质,熟练掌握不等式的性质是解题的关键.
10.D
【分析】用科学记数法表示较大的数时,一般形式为,其中,n为整数
【详解】解:万用科学记数法表示为.
故选:D.
【点睛】本题考查了科学记数法,科学记数法的表示形式为的形式,其中,n为整数.确定n的值时,要看把原来的数,变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值时,n是正数;当原数的绝对值时,n是负数,确定a与n的值是解题的关键.
11.58m
【分析】延长AB和CD分别与直线OF交于点G和点H,则,再根据图形应用三角函数即可求解.
【详解】解:延长AB和CD分别与直线OF交于点G和点H,则.
又∵,
∴四边形ACHG是矩形.
∴.
由题意,得.
在中,,
∴(m)﹒
∵是的外角,
∴.
∴.
∴m.
在中,
∴(m).
∴.
答:楼AB与CD之间的距离AC的长约为58m.
【点睛】本题主要考查三角函数的综合应用,正确构造直角三角形并应用三角函数进行求解是解题的关键.
12.(1)50人
(2)见解析
(3)20000人
【分析】(1)根据统计图找出活动时间为0.5小时的人数和百分比,计算得到答案;
(2)求出户外活动时间为1.5小时的人数,补充频数分布直方图;
(3)利用总人数乘以不少于1.5小时的人数的百分比即可得到答案.
(1)
解:调查的总人数是(人).
(2)
实践1.5小时的人数是(人),
补全图形如下:
(3)
参加户外活动不少于1.5小时的人数是(人).
【点睛】本题考查读频数分布直方图的能力和利用统计图获取信息的能力;利用样本估计总体,利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.
13.(1)见解析
(2)
(3),
(4)
【分析】(1)根据两角对应相等即可证明△OBE∽△OFB;
(2)根据角之间的关系即可求解;
(3)分OE∥BC和OE∥BF两种情况,分别求解即可;
(4)作EP∥OC交OB的延长线于点P,则OG=GB=GF,∠BOC=∠P=∠EOP,OB=BP,可得,设OG=GB=GF=1,则EG=3,,,.
【详解】(1)证明:∵,
∴,
∵是的切线,
∴,
∴.
(2)解:∵,
∴,
∵,
∴,
∴,
∴,即.
(3)解:①如图1,当时,,
∴是等边三角形,,,,
作的延长线于点H,,,,
在中,;
②如图2,当时,
∵,
∴,
∴,
在中,.
(4)解:如图3,作交的延长线于点P,
易知,,
不妨设,
则,,,
.
【点睛】本题考查了相似三角形的判定与性质,切线的性质,勾股定理,三角函数的定义等知识,熟练掌握这些知识点并会应用是解决问题的关键.
14.(1)见解析
(2)见解析
【分析】(1)根据轴对称与中心对称的性质即可求解;
(2)根据等边三角形的性质,以及菱形的性质,画出其中一个图形即可.
(1)
解:四边形是菱形,
根据轴对称的性质找在菱形的边上找到对称的两点,进而根据对角相等的且互相平分的四边形是矩形,画图如下,画出其中一个图形即可.
(2)
如图,根据菱形的判定,对角线互相垂直,画出其中一个图形即可.
【点睛】本题考查了中心对称与轴对称,等边三角形的性质,菱形的性质,矩形的性质,综合运用以上知识是解题的关键.
15.(1)见解析
(2)
【分析】(1)根据圆周角定理得到∠ADC=∠ABC,进而推出∠ADC=∠CAD,根据等腰三角形的性质得到∠OAD=∠ODA,根据角的和差即可得解;
(2)连接CO,并延长交AD于点F,利用SSS证明△AOC≌△DOC,则∠ACF=∠DCF,根据等腰三角形三线合一的性质得出CF⊥AD,AD=2AF,根据勾股定理得到BC=,解直角三角形得到AF=3,据此即可得解.
【详解】(1)证明:∵,,
∴,
∵,
∴,
∴.
(2)连接,并延长交于点F,
∵,
∴,
在中,,
∴△AOC≌△DOC(SSS),
∴∠ACF=∠DCF,
∴,,
∵是的直径,
∴,
∴
在中,,
∴.
【点睛】此题考查了全等三角形的判定与性质、圆周角定理,熟练掌握全等三角形的判定与性质是解题的关键.
16.(1)
(2),
(3)
【分析】(1)把点(1,8)代入抛物线解析式即可;
(2)根据抛物线对称轴的公式可求得对称轴,根据抛物线的对称性可得结论;
(3)根据抛物线解析式可求得OC的长及顶点D的坐标,再根据OP=4CP可求得OP的长,再由点关于直线对称列出方程,求解得出a的值,进而求出点M和点N的坐标,即可求出MN的长.
【详解】(1)把点代入抛物线得:,
整理得:;
(2)该抛物线的对称轴为直线,
过顶点D作轴于点E,交于点H,
∵轴,由对称性可知,,
∴.
(3)易知点,则,
∵,
∴,
又,
∴点,
∵点D关于的对称点的纵坐标为,
∴,
解得:,
此时,抛物线解析式为,
令,
解得:或x=5,
∴点M,N坐标分别为,
∴.
【点睛】本题主要考查抛物线的对称轴公式,顶点坐标,抛物线的对称性等内容,属于二次函数综合题,中等难度,解题关键是掌握相关性质定理.
17.(1)200,108
(2)估计该校学生中“中度近视”的人数约为480人;
(3)甲和乙两名学生同时被选中的概率为.
【分析】(1)从所取样本中根据“正常”的人数和所占比例求出所抽取的学生总人数;根据“中度近视”的人数求出所占比例,乘以360°即可求解;
(2)由全校共有学生人数乘以“中度近视”人数所占的比例即可;
(3)画树状图列出所有等可能结果,再利用概率公式计算可得.
【详解】(1)解:所抽取的学生总数为m=48÷24%=200(人),
n= 360×=108,
故答案为:200,108;
(2)解:1600×=480(人),
即估计该校学生中“中度近视”的人数约为480人;
(3)解:画树状图为:
共有12种等可能的结果数,其中甲和乙两名学生同时被选中的结果数为2,
所以甲和乙两名学生同时被选中的概率为=.
【点睛】本题考查扇形统计图、统计表以及用样本估计总体以及列表法与树状图法等知识;利用列表法或树状图法展示所有等可能的结果n,再从中选出符合事件A或B的结果数目m,然后利用概率公式计算事件A或事件B的概率.
18.
【分析】,根据旋转的性质可得△ABC≌△DBE,所以,用扇形面积公式计算即可.
【详解】解:由题意可得:∠CAB=30°,根据旋转的性质可得:∠BDE=∠CAB=30°,△ABC≌△DBE;
∵DEAB
∴∠BDE=∠ABD=30°
∵
∴
故答案为:.
【点睛】本题考查了阴影部分面积的计算、旋转的性质、平行的性质、扇形面积公式等知识,解题的关键是把不规则阴影部分的面积转化为规则图形的面积.
19.
【分析】(1)连接BD,分别解和,得到,进而利用勾股定理即可求解;
(2)由,,得到ABDO,即可得出度数的最大值.
【详解】解:(1)连接BD,
∵,,
∴,
∵点是的中点,,
∴,
,
,
∴,
∵平分,
∴,
∵,
∴,
∴,
,
∴.
故答案为:.
(2)由(1)可知,
又∵,
∴ABDO,
∴,
又∵,
∴,
∴,
∵,
∴当时,有最大值,
∴的最大值为:.
故答案为:.
【点睛】本题考查解直角三角形.添加适当辅助线是本题解题的关键.
20.105°/105度
【分析】根据AP为∠BAC的角平分线,先求出∠BAP的度数,再通过三角形内角和为180°,求出∠APB的度数即可.
【详解】解:通过图中作图痕迹可知AP为∠BAC的角平分线,
,
在△ABP中,,
故答案为:105°.
【点睛】本题考查了尺规作图画角平分线,三角形内角和定理等,能够通过图中作图痕迹得到AP为∠BAC的角平分线是解题的关键.
21. 矩形; .
【分析】(1)由题意,由折叠的性质得到,,则得到,同理可求,即可得到结论成立;
(2)设,,则求出,得到AH和DH的长度,然后证明,从而求出HF的长度,过点H作HI⊥BC于点I,则HI=AB,BI=AH,求出FI的长度,再利用勾股定理,即可求出答案.
【详解】解:(1)根据题意,由折叠的性质,
,,
∴,
即,
同理可求:,,
∴四边形EFGH是矩形;
故答案为:矩形;
(2)∵,
设,,
由折叠的性质,则AH=HJ,HD=HK,
∵,
∴,解得:,
∴,;
由(1)可知,四边形EFGH是矩形,
∴EF=HG,EF∥HG,
∴∠EFJ=∠GHK,
∵∠EJF=∠GKH=90°,
∴△EFJ≌△GHK,
∴FJ=HK,
∵HD=HK,FB=FJ,
∴HD=HK=FB=FJ=;
∴,
如图,过点H作HI⊥BC于点I,则HI=AB,BI=AH,
∴,
在直角中,由勾股定理则
;
∴;
故答案为:.
【点睛】本题考查了折叠的性质,矩形的判定和性质,全等三角形的判定和性质,勾股定理,解题的的关键是熟练掌握所学的知识,正确的分析题意.
22. 10 /4.5
【分析】根据方差和平均数的变化规律可得:数据3x1+1、3x2+1、3x3+1、3x4+1、3x5+1的平均数是3×3+1,方差是方差为(3×)2,再进行计算即可.
【详解】解:∵数据x1、x2、x3、x4、x5的平均数是3,方差为,
∴新数据3x1+1、3x2+1、3x3+1、3x4+1、3x5+1的平均数是3×3+1=10,
方差为,
故答案为:10,.
【点睛】此题考查了方差的特点,若在原来数据前乘以同一个数,平均数也乘以同一个数,而方差要乘以这个数的平方,若数据都加上一个数(或减去一个数)时,方差不变,即数据的波动情况不变.
23./
【分析】根据题意可得这两个扇形可组合成一个大扇形,且这两个扇形的的圆心角的和为90°,再根据扇形的面积公式,即可求解.
【详解】解:根据题意得:两个扇形的半径相等均为1,
∴这两个扇形可组合成一个大扇形,
∵这两个扇形的的圆心角正好是直角三角形的两个锐角,
∴这两个扇形的的圆心角的和为90°,
∴这两个小扇形的面积之和为.
故答案为:
【点睛】本题主要考查了学生的观察能力及计算能力.理解求不规则的图形的面积,可以转化为几个规则图形的面积的和或差来求是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
