【考前必刷】浙江地区2023年中考数学全真模拟卷10(含解析)
文档属性
| 名称 | 【考前必刷】浙江地区2023年中考数学全真模拟卷10(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 4.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-03 22:26:22 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
【考前必刷】浙江地区中考数学全真模拟卷10
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,在中,直径与弦相交于点,连接弦,,.若,给出下列结论:①;②,则下列判断正确的是( )
A.①,②都对 B.①,②都错 C.①对,②错 D.①错,②对
2.某校科技小组进行野外考察,利用铺垫木板的方式,通过了一片烂泥湿地.他们发现,当人和木板对湿地的压力一定时,人和木板对地面的压强随着木板面积的变化而变化.若人和木板对湿地地面的压力合为,为安全起见压强P不超过,则下列说法正确的是( )
A.当S越来越大时,P也越来越大 B.当S为时,P是
C.S最多为 D.S最少为
3.设,则下列式子不正确的是( )
A. B. C. D.
4.下列四个图案是历届世界杯足球赛会徽图案上的一部分图形,其中是轴对称图形的是( )
A. B. C. D.
5.如图,是函数的图象,通过观察图象得出了如下结论:
①当时,y随x的增大而增大;
②该函数图象与坐标轴有三个交点;
③该函数的最大值是6,最小值是:
④当时,不等式的解为.
以上结论中正确的有( )
A.1 B.2 C.3 D.4
6.《张丘建算经》是中国古代数学著作,其中提出了许多数学问题,比如:“今有甲乙怀钱各不知其数,甲得乙十钱,多乙余钱五倍;乙得甲十钱,适等;问甲乙怀钱各几何?”可以理解为:甲乙两人各有一些钱,若乙给甲10元,则甲的钱比乙;若甲给乙10元,则两人的钱一样多.不妨设甲原有钱元,乙原有钱元,则可列方程组为( )
A. B.
C. D.
7.如图,在中,,点分别在边上,连接,且满足.设,则关于x,y的关系式正确的是( )
A. B. C. D.
8.下列计算正确的是( )
A. B. C. D.
9.已知点,,(其中)都在反比例函数的图象上,则,,的大小关系为( )
A. B. C. D.
10.学校开设了烹饪课程后,某班七名学生学会烹饪的菜品种数依次为;,,,,,,,则这组数据的众数,中位数分别是( )
A., B., C., D.,
二、填空题
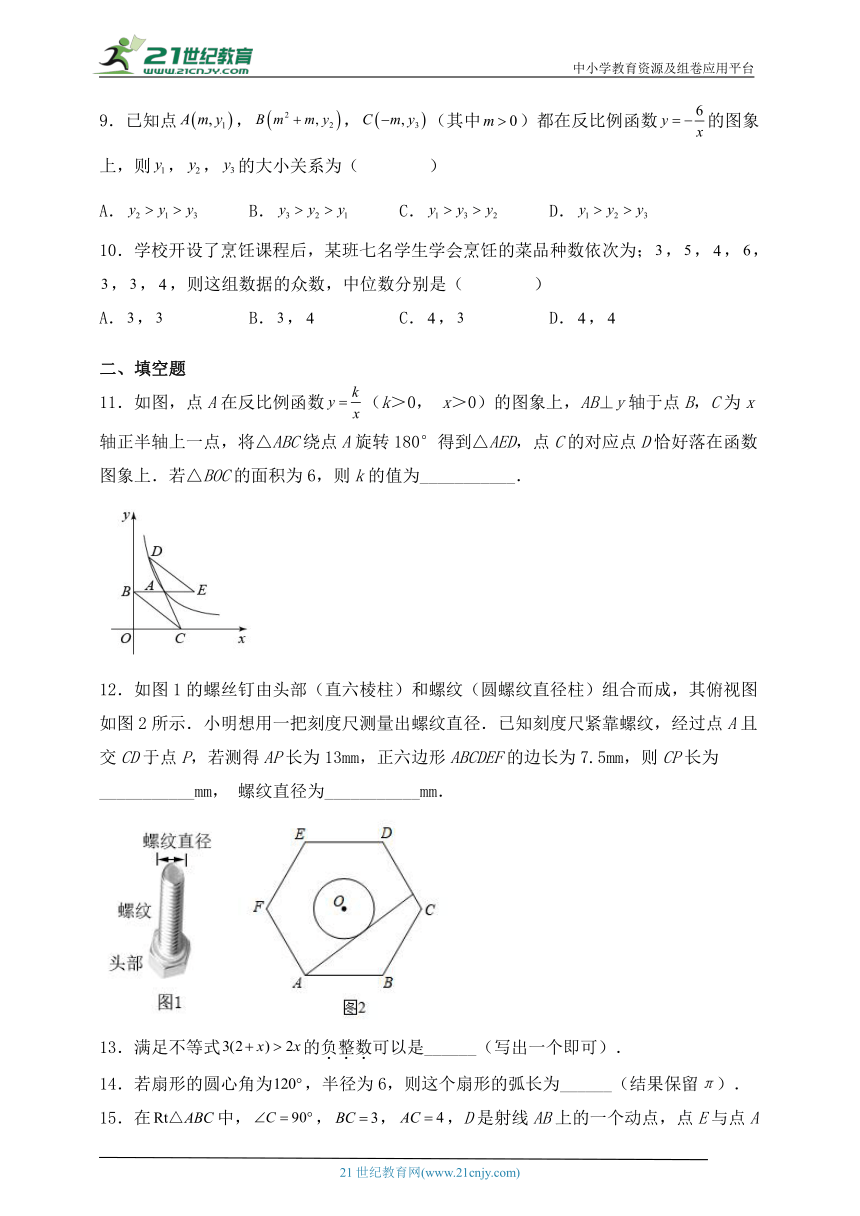
11.如图,点A在反比例函数(k>0, x>0)的图象上,AB⊥y轴于点B,C为x轴正半轴上一点,将△ABC绕点A旋转180°得到△AED,点C的对应点D恰好落在函数图象上.若△BOC的面积为6,则k的值为___________.
12.如图1的螺丝钉由头部(直六棱柱)和螺纹(圆螺纹直径柱)组合而成,其俯视图如图2所示.小明想用一把刻度尺测量出螺纹直径.已知刻度尺紧靠螺纹,经过点A且交CD于点P,若测得AP长为13mm,正六边形ABCDEF的边长为7.5mm,则CP长为___________mm, 螺纹直径为___________mm.
13.满足不等式的负整数可以是______(写出一个即可).
14.若扇形的圆心角为,半径为6,则这个扇形的弧长为______(结果保留π).
15.在中,,,,D是射线AB上的一个动点,点E与点A关于直线CD对称,当______时,为直角三角形.
16.在中,,,为边的中点,以点为圆心,长为半径作弧,交直线于点,连结.则的度数是______.
三、解答题
17.如图,在平面直角坐标系中,过点、两点的抛物线的顶点C在x轴正半轴上.
(1)求抛物线的解析式;
(2)求点C的坐标;
(3)为线段AB上一点,,作轴交抛物线于点M,求PM的最大值与最小值.
18.定义:函数图像上到两坐标轴的距离都不大于的点叫做这个函数图像的“n阶方点”.例如,点是函数图像的“阶方点”;点是函数图像的“2阶方点”.
(1)在①;②;③三点中,是反比例函数图像的“1阶方点”的有___________(填序号);
(2)若y关于x的一次函数图像的“2阶方点”有且只有一个,求a的值;
(3)若y关于x的二次函数图像的“n阶方点”一定存在,请直接写出n的取值范围.
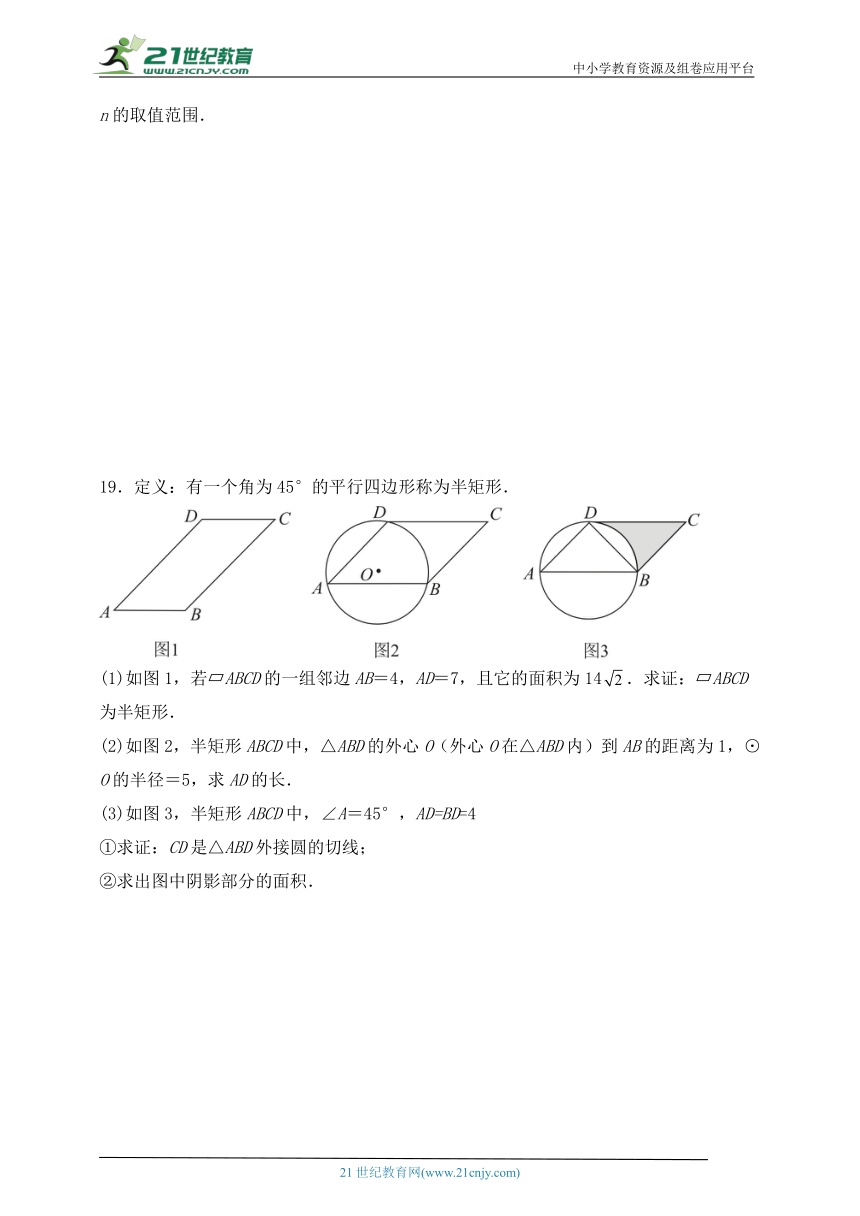
19.定义:有一个角为45°的平行四边形称为半矩形.
(1)如图1,若 ABCD的一组邻边AB=4,AD=7,且它的面积为14.求证: ABCD为半矩形.
(2)如图2,半矩形ABCD中,△ABD的外心O(外心O在△ABD内)到AB的距离为1,⊙O的半径=5,求AD的长.
(3)如图3,半矩形ABCD中,∠A=45°,AD=BD=4
①求证:CD是△ABD外接圆的切线;
②求出图中阴影部分的面积.
20.公路上正在行驶的甲车发现前方20m处沿同一方向行驶的乙车后,开始减速,减速后甲车行驶的路程s(单位:m)、速度v(单位:m/s)与时间t(单位:s)的关系分别可以用二次函数和一次函数表示,其图象如图所示.
(1)直接写出s关于t的函数关系式_____________和v关于t的函数关系式_____________(不要求写出t的取值范围)
(2)当甲车减速至9m/s时,它行驶的路程是多少?
(3)若乙车以10m/s的速度匀速行驶,两车何时相距最近,最近距离是多少?
21.如图,一次函数的图像与轴,轴分别交于,两点.
(1)求一次函数的解析式;
(2)若为轴上一动点,当的面积为6时,求点的坐标.
22.如图,将矩形ABCD沿AE折叠,使点D落在BC边的点F处.
(1)求证:△ABF∽△FCE;
(2)已知AB=3,AD=5,求的值.
23.某校积极落实“双减”政策,将要开设拓展课程,为让学生可以根据自己的兴趣爱好选择最喜欢的课程,进行问卷调查,问卷设置以下四种选项:A(综合模型)、B(摄影艺术)、C(音乐鉴赏)、D(劳动实践),随机抽取了部分学生进行调查,每名学生必须且只能选择其中最喜欢的一种课程,并将调查结果整理绘制成如下不完整的统计图.
根据以上信息,解答下列问题:
(1)此次被调查的学生人数为________名;
(2)直接在答题卡中补全条形统计图;
(3)求拓展课程D(劳动实践)所对应的扇形的圆心角的度数;
(4)根据抽样调查结果,请你估计该校800名学生中,有多少名学生最喜欢C(音乐鉴赏)拓展课程.
参考答案:
1.A
【分析】根据已知条件设,则,根据直径所对的圆周角是直角得出,根据同弧所对的圆周角相等得出,根据三角形内角和定理以及对顶角相等得出,根据等角对等边即可判断①,连接,证明,根据相似三角形的性质,即可得出②,从而求解.
【详解】解:如图所示,连接,
∵,设,则,
∵,
∴,
∵是直径,
∴,
在中,,
∴,
在中,,
,
∴,
∴;故①正确;
∵,
∴,
∴,
又,
∴,
∴,
即,
∴,故②正确,
故选:A.
【点睛】本题考查了同弧所对的圆周角相等,直径所对的圆周角是直角,相似三角形的性质与判定,等腰三角形的性质与判定,熟练掌握圆周角定理是解题的关键.
2.D
【分析】根据题意得到反比例函数式,再根据干比例函数式逐一进行判断即可得到答案.
【详解】解:由题意可知,压力一定时,压强和木板面积成反比,
人和木板对湿地地面的压力合为,
,
是S的反比例函数,
当S越来越大时,P也越来越小,
选项A不符合题意;
当S为时,,
选项B不符合题意;
压强P不超过,
,
,
S最少为,
选项C不符合题意,选项D符合题意,
故选D.
【点睛】本题考查了反比例函数的应用,根据题意写出反比例函数式是解题关键.
3.B
【分析】利用不等式的基本性质逐项判断即可.
【详解】解:A、由可得:,原变形正确,故此选项不符合题意;
B、由可得:,原变形错误,故此选项符合题意;
C、由可得:,原变形正确,故此选项不符合题意;
D、由可得:,原变形正确,故此选项不符合题意;
故选B.
【点睛】本题考查了不等式的性质,不等式的基本性质:①不等式的两边同时乘以(或除以)同一个正数,不等号的方向不变;②不等式的两边同时乘以(或除以)同一个负数,不等号的方向改变;③不等式的两边同时加上(或减去)同一个数或同一个含有字母的式子,不等号的方向不变.
4.A
【分析】根据轴对称图形的定义判断选择即可.
【详解】解:A选项是轴对称图形,符合题意;
B选项不是轴对称图形,不符合题意;
C选项不是轴对称图形,不符合题意;
D选项不是轴对称图形,不符合题意;
故选:A.
【点睛】本题考查了轴对称图形即沿着某条直线折叠,直线两旁的部分完全重合,熟练掌握定义是解题的关键.
5.C
【分析】根据函数图象的性质进行逐项分析即可.
【详解】解:由题中图象可知,该函数图象与x轴有三个交点,故②正确;
令,
解得:,,,
即该函数图象与x轴的三个交点坐标分别为,,,
∴结合图形可知,当时,y随x的增大而增大,故①正确;
∵自变量的范围是,
∴结合图象可知,当时,函数取得最大值,最大值为,
当时,函数取得最小值,最小值为,故③正确;
由图象可知,当时,函数图象在x轴上方的部分为或,
∴不等式的解为或,故④错误;
综上所述,正确的有①②③,共3个.
故选:C.
【点睛】本题考查函数图象的性质,掌握函数图象与坐标轴的交点的求法与意义,理解判断函数性质的方法是解题关键.
6.B
【分析】由题意知,,进而可得结果.
【详解】解:由题意知,,
故答案为:B.
【点睛】本题考查了二元一次方程组的应用.解题的关键在于根据题意正确的列方程组.
7.D
【分析】先根据等腰三角形的性质与判定得出,,,再根据平角定义得到和的关系式,根据三角形内角和得到和的关系式,结合求解即可.
【详解】解:∵,
∴,
∵,
∴,
∴,
∴,
又∵,
∴,即,
故选:D.
【点睛】本题考查了等腰三角形的性质与判定,三角形内角和定理和平角定义,熟练掌握相关知识点是解题的关键.
8.D
【分析】分别根据同底数幂的乘除法运算法则、合并同类项、幂的乘方运算法则逐项排查即可.
【详解】解:A. ,所以本选项计算错误,不符合题意;
B. ,所以本选项计算错误,不符合题意;
C.,所以本选项计算错误,不符合题意;
D.,所以本选项计算正确,符合题意.
故选:D.
【点睛】本题主要考查了同底数幂的乘法和除法、合并同类项、幂的乘方等知识点,灵活运用相关运算法则是解题的关键.
9.B
【分析】根据反比例函数图象上点的坐标特征,将点,,分别代入函数,求得的,然后比较它们的大小.
【详解】解:把,,分别代入:,
,
∵,
∴,
∴.
故选:B.
【点睛】本题考查的是反比例函数的性质,考查根据自变量的值判断函数值的大小,掌握判断方法是解题的关键.
10.B
【分析】根据中位数与众数的定义即可求解.中位数:把一组数据按从小到大的顺序排列,在中间的一个数字(或者两个数字的平均值)叫做这组数据的中位数.众数:在一组数据中出现次数最多的数.
【详解】解:将数据,,,,,,,
从小到大排列为:,,,,,,
∴众数为,中位数为,
故选:B.
【点睛】本题考查了中位数与众数的定义,熟练掌握中位数与众数的定义是解题的关键.
11.8
【分析】由旋转得到△ABC≌△AED,AC=AD,即点A为CD的中点,设B(0,m),则OB=m,通过面积表示C的坐标,进一步表示出A,D的坐标,将D代入反比例函数,求出k即可.
【详解】∵AB⊥y轴,OC⊥y轴,
∴AB∥OC,
∵△ABC绕点A旋转180°得到△AED,
∴△ABC≌△AED,
∴AC=AD,即点A为CD的中点,
设B(0,m),则OB=m,
∵,
∴,
∴C的坐标为,
∵点A在上,且AB⊥y轴,
∴A的纵坐标为m,
∴A ,
∵点A为CD的中点,
∴D,即,
∵D在上,∴,
∴4k-24=k,
∴k=8.
故答案为:8.
【点睛】本题考查了旋转和反比例函数的图象及性质,解题的关键是利用参数表示出图象上的点带入其表达式.
12. 0.5/ /
【分析】连接AC,过点B作BM⊥AC于点M,设正六边形ABCDEF的中心为O,连接AD,知A、O、D共线,过点O作ON⊥AP于点N,过D作DH⊥AP于H,利用正六边形的性质先、勾股定理求出AC的长度,结合AP的长度求出PC长度;再根据△AON∽△ADH知DH=2ON,设PH=x,利用勾股定理得到关于x的方程,再用勾股定理求出DH及ON长度即可.
【详解】解:连接AC,过点B作BM⊥AC于点M,设正六边形ABCDEF的中心为O,连接AD,由题意知,A、O、D共线,过点O作ON⊥AP于点N,过D作DH⊥AP于H,如图,
则,
由DH⊥AP知,ON∥DH,
∴△AON∽△ADH,
∴,
∵O是AD中点,
∴DH=2ON,
在正六边形ABCDEF中,mm,,
,,
在中,(mm),
(mm),
在中,mm,由勾股定理得,(mm),
∴DP=7mm,
∵正六边形的半径与边长相等,
mm,AD=15mm,
设PH=xmm,则AH=(13+x)mm,
在Rt△DPH和Rt△ADH中,由勾股定理得:
,
即,
即,
解得:x=,
∴DH=mm,
∴ON=mm,
故直径为
故答案为:0.5;.
【点睛】本题主要考查了正六边形的性质、勾股定理、相似三角形性质、解直角三角形以及等腰三角形的性质等知识点.解题关键是根据题意作出垂线,解直角三角形.
13.(答案不唯一)
【分析】先求出不等式的解集,再在解集中任选一个负整数即可.
【详解】解:解不等式得.
∴满足不等式的负整数可以是(答案不唯一).
故答案为:.
【点睛】本题考查求不等式的整数解,熟练掌握该知识点是解题关键.
14.
【分析】根据弧长的公式进行计算即可.
【详解】解:根据弧长的公式,
得到:.
故答案是:.
【点睛】本题主要考查了弧长的计算,熟记弧长公式是解题的关键.
15.0.8或5.6
【分析】由△ADE为等腰三角形,且为直角三角形,则只能∠ADE=90°,且△ADE为等腰直角三角形,
①D在A、B之间时,易证△BCG∽△BAC,得出,得出BG=1.8,利用勾股定理,得出DG=CG=2.4,进而得出AD的长;
②D在A、B之外时,易证△BCG∽△CAF,得出,令BG=3x,则CF=4x,进而表示出BD=,AD=5+,得出DF=,由GC=DF-DG-CF=,利用勾股定理GC2+BG2=BC2,求出x,进而得出AD的长.
【详解】解:∵∠ADE=90°,AD=DE,
∴△ADE为等腰直角三角形,
∴∠ADF=45°,
在中,,,,
∴AB==5,
①D在A、B之间时,
过点C作CG⊥AB于点G,
∴∠BGC=90°,
又∠ACB=90°,
∴△BCG∽△BAC,
∴,
又,,
∴BG=1.8,
在Rt△BCG中BG2+CG2=BC2,
∴1.82+CG2=32,
解得CG=2.4,
∵∠CDG=∠DCG=45°,
∴DG=CG=2.4,
∴AD=AB-DG-BG=5-2.4-1.8=0.8;
②D在A、B之外时,
过点B作BG⊥CD于点G,连接EC
∴∠BGC=90°,
∵点E与点A关于直线CD对称,
∴DF垂直平分AE,
∴∠AFD=90°,AD=DE,
又,
∵∠1+∠BCG=90°,∠2+∠BCG=90°,
∴∠1=∠2,
∴△BCG∽△CAF,
∴,
令BG=3x,则CF=4x,
∵BG⊥CD,
∴△BDG为等腰直角三角形,
∴BG=DG=3x,BD==,
∴AD=5+,
∴DF=,
∴GC=DF-DG-CF=,
在Rt△BCG中GC2+BG2=BC2,
∴()2+(3x)2=32
解得x1=, x2=,
∴当x1=时,GC=<0,
∴x=,
∴AD=5+=5.6.
综上可知,AD的长为0.8或5.6.
【点睛】本题考查轴对称的性质,勾股定理解直角三角形,相似三角形的判定和性质,等腰直角三角形的性质,熟练掌握以上内容是解决问题的关键.
16.25°或65°
【分析】根据等腰三角形的性质可以得到各内角的关系,然后根据题意,画出图形,利用分类讨论的方法求出的度数即可.
【详解】解:如图
,
,
为边的中点,
,,
当点在点的左侧时,
,,
,
;
当点在点的右侧时,
,,
,
,
的度数为 或.
故答案为: 或.
【点睛】本题主要考查等腰三角形的性质,圆的定义,解答本题的关键是画出合适的辅助线,利用分类讨论的方法解答.
17.(1)
(2)
(3)最大值是,最小值是4
【分析】(1)根据题意设抛物线的解析式为,然后把点、代入关系式进行计算即可解答;
(2)把代入(1)中所求的抛物线的解析式进行计算即可解答;
(3)先求出解析式,然后计算当,,,的长度,然后设,,表示出的值,然后再进行计算即可解答.
【详解】(1)解:∵抛物线的顶点在轴正半轴上,
∴设抛物线的解析式为,
把点、代入中可得:,
解得:舍去或,
∴,
∴抛物线的解析式为:;
(2)把代入中可得:,
∴,
∴点的坐标为;
(3)设的解析式为:,
把点、代入中可得:,
解得:,
∴的解析式为:,
∵点为线段上一点,点为抛物线上一点,且,轴,
∴当时,,,
∴,
当时,,,
∴,
当时,,,
∴,
设,,
∴,
当时,的最大值为:,
∴的最大值是,最小值是4.
【点睛】本题考查了二次函数的最值,待定系数法求二次函数解析式,二次函数的性质,二次函数图象上点的坐标特征,准确熟练地进行计算是解题的关键.
18.(1)②③
(2)3或;
(3)
【分析】(1)根据“n阶方点”的定义逐个判断即可;
(2)如图作正方形,然后分a>0和a<0两种情况,分别根据“2阶方点”有且只有一个判断出所经过的点的坐标,代入坐标求出a的值,并舍去不合题意的值即可得;
(3)由二次函数解析式可知其顶点坐标在直线y=-2x+1上移动,作出简图,由函数图象可知,当二次函数图象过点(n,-n)和点(-n, n)时为临界情况,求出此时n的值,由图象可得n的取值范围.
【详解】(1)解:∵点到x轴的距离为2,大于1,
∴不是反比例函数图象的“1阶方点”,
∵点和点都在反比例函数的图象上,且到两坐标轴的距离都不大于1,
∴和是反比例函数图象的“1阶方点”,
故答案为:②③;
(2)如图作正方形,四个顶点坐标分别为(2,2),(-2,2),(-2,-2),(2,-2),
当a>0时,若y关于x的一次函数图象的“2阶方点”有且只有一个,
则过点(-2,2)或(2,-2),
把(-2,2)代入得:,解得:(舍去);
把(2,-2)代入得:,解得:;
当a<0时,若y关于x的一次函数图象的“2阶方点”有且只有一个,
则过点(2,2)或(-2,-2),
把(2,2)代入得:,解得:;
把(-2,-2)代入得:,解得:(舍去);
综上,a的值为3或;
(3)∵二次函数图象的顶点坐标为(n,),
∴二次函数图象的顶点坐标在直线y=-2x+1上移动,
∵y关于x的二次函数图象的“n阶方点”一定存在,
∴二次函数的图象与以顶点坐标为(n,n),(-n,n),(-n,-n),(n,-n)的正方形有交点,
如图,当过点(n,-n)时,
将(n,-n)代入得:,
解得:,
当过点(-n,n)时,
将(-n,n)代入得:,
解得:或(舍去),
由图可知,若y关于x的二次函数图象的“n阶方点”一定存在,n的取值范围为:.
【点睛】本题考查了新定义,反比例函数图象上点的坐标特点,一次函数的图象和性质,二次函数的图象和性质,正确理解“n阶方点”的几何意义,熟练掌握数形结合思想的应用是解题的关键.
19.(1)见解析
(2)
(3)①见解析,②12﹣2π
【分析】(1)由S ABCD=AB DH=4×DH=14,解得DH=,进而求解;
(2)连接OD、OB、BD,则∠BDO=2∠DAB=90°,则BD=BO=5,进而求解;
(3)①证明△ABD为等腰直角三角形,得到OD是圆的半径且OD⊥CD,即可求解;
②由阴影部分的面积=S ABCD﹣S△ADO﹣S扇形ODB,即可求解.
【详解】(1)解:过点D作DH⊥AB交AB的延长线于点H,
∵S ABCD=AB DH=4×DH=14,解得DH=,
则AH==DH,
∴∠A=45°,
∴ ABCD为半矩形;
(2)解:连接OD、OB、BD,
则∠BDO=2∠DAB=90°,则BD=BO=5,
过点O作OH⊥AB于点H,则BH==AB,
则AB=4,
过点B作BE⊥AD于点E,
则BE=AB=4=AE,
在Rt△BDE中,DE=,
∴AD=AE+DE=4+;
(3)解:①过点D作DO⊥AB于点O,
∵∠A=45°,AD=BD=4,
故AB=4,则△ABD为等腰直角三角形,
则OD=AB=2,
∵ABCD,DO⊥AB,
∴OD⊥CD,
∴CD是△ABD外接圆的切线;
②阴影部分的面积=S ABCD﹣S△ADO﹣S扇形ODB
=4×2﹣×2×2﹣×π×(2)2
=12﹣2π.
【点睛】本题为圆的综合题,主要圆切线的判定与性质、新定义、平行四边形的性质、解直角三角形、面积的计算等,有一定的综合性,难度适中.
20.(1)s=﹣t2+16t,v=﹣t+16
(2)当甲车减速至9m/s时,它行驶的路程是87.5m
(3)6秒时两车相距最近,最近距离是2m
【分析】(1)根据图象信息,利用待定系数法分别求出一次函数和二次函数解析式即可;
(2)把代入一次函数解析式求出,再把的值代入二次函数解析式求出即可;
(3)根据当时,甲车的速度为16,当时,两车之间的距离逐渐变大,当时,两车之间的距离逐渐变小,得出当时,两车之间距离最小,代入计算即可.
【详解】(1)解:由图可知:二次函数图象经过原点,
设二次函数表达式为,一次函数表达式为,
二次函数经过,,
,解得:,
二次函数表达式为.
一次函数经过,,
,解得:,
一次函数表达式为.
故答案为:,;
(2)解:,
当时,
,解得,
,
当时,,
当甲车减速至9时,它行驶的路程是87.5;
(3)解:当时,甲车的速度为16,
当时,两车之间的距离逐渐变大,
当时,两车之间的距离逐渐变小,
当时,两车之间距离最小,
将代入中,得,
将代入中,得,
此时两车之间的距离为:,
秒时两车相距最近,最近距离是.
【点睛】本题考查了二次函数与一次函数的实际应用,解题的关键是理解题意,读懂函数图象,求出函数表达式.
21.(1)
(2)或
【分析】(1)待定系数法求解析式即可求解;
(2)设,根据的面积为6建立方程,解方程即可求解.
【详解】(1)解:∵一次函数的图像与轴,轴分别交于,两点,
∴,
解得,
一次函数的解析式为;
(2)解:设,
,,
,
当的面积为6时,,
解得或,
或.
【点睛】本题考查了待定系数法求一次函数解析式,三角形的面积,数形结合是解题的关键.
22.(1)见解析
(2)
【分析】(1)由折叠的性质得,进而得出,即可证明△ABF∽△FCE;
(2)设,则,由折叠的性质知,,,利用勾股定理求出BF,进而求出CF,在△CEF中根据勾股定理列方程求出x,则.
【详解】(1)证明:∵四边形ABCD是矩形,
∴,
由折叠的性质知,,
∴,,
∴.
在△ABF和△FCE中,
,
∴△ABF∽△FCE;
(2)解:∵矩形ABCD中,AB=3,AD=5,
∴,,
设,则,
由折叠的性质知,,,
由勾股定理得,,
∴,
在△CEF中,由勾股定理得:,
即,
解得,
∴,
∴.
【点睛】本题考查矩形的性质,折叠的性质,相似三角形的判定,勾股定理,三角函数解直角三角形等知识点,利用折叠的性质得出,,是解题的关键.
23.(1)120
(2)见解析
(3)72
(4)320名
【分析】(1)先求出B的人数,再将各项人数相加即可.
(2)见解析
(3)根据D的百分比乘以圆心角即可.
(4)求出C所占的百分比,乘以800.
【详解】(1)解:根据扇形统计图中,B是A的3倍
故喜欢B的学生数为(名)
统计调查的总人数有:12+36+48+24=120(名).
(2)
(3)由条形统计图可知:
D的人数是A的2倍,故D占总人数的20%
所以D所占圆心角为20%
答:课程D所对应的扇形的圆心角的度数为72.
(4)若有800名学生,则喜欢C的学生数有:
(名)
答:有320名学生最喜欢C拓展课程.
【点睛】本题考查扇形统计图与条形统计图相关内容,注意从图中获取信息,分析图中数据之间的数量关系是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
【考前必刷】浙江地区中考数学全真模拟卷10
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,在中,直径与弦相交于点,连接弦,,.若,给出下列结论:①;②,则下列判断正确的是( )
A.①,②都对 B.①,②都错 C.①对,②错 D.①错,②对
2.某校科技小组进行野外考察,利用铺垫木板的方式,通过了一片烂泥湿地.他们发现,当人和木板对湿地的压力一定时,人和木板对地面的压强随着木板面积的变化而变化.若人和木板对湿地地面的压力合为,为安全起见压强P不超过,则下列说法正确的是( )
A.当S越来越大时,P也越来越大 B.当S为时,P是
C.S最多为 D.S最少为
3.设,则下列式子不正确的是( )
A. B. C. D.
4.下列四个图案是历届世界杯足球赛会徽图案上的一部分图形,其中是轴对称图形的是( )
A. B. C. D.
5.如图,是函数的图象,通过观察图象得出了如下结论:
①当时,y随x的增大而增大;
②该函数图象与坐标轴有三个交点;
③该函数的最大值是6,最小值是:
④当时,不等式的解为.
以上结论中正确的有( )
A.1 B.2 C.3 D.4
6.《张丘建算经》是中国古代数学著作,其中提出了许多数学问题,比如:“今有甲乙怀钱各不知其数,甲得乙十钱,多乙余钱五倍;乙得甲十钱,适等;问甲乙怀钱各几何?”可以理解为:甲乙两人各有一些钱,若乙给甲10元,则甲的钱比乙;若甲给乙10元,则两人的钱一样多.不妨设甲原有钱元,乙原有钱元,则可列方程组为( )
A. B.
C. D.
7.如图,在中,,点分别在边上,连接,且满足.设,则关于x,y的关系式正确的是( )
A. B. C. D.
8.下列计算正确的是( )
A. B. C. D.
9.已知点,,(其中)都在反比例函数的图象上,则,,的大小关系为( )
A. B. C. D.
10.学校开设了烹饪课程后,某班七名学生学会烹饪的菜品种数依次为;,,,,,,,则这组数据的众数,中位数分别是( )
A., B., C., D.,
二、填空题
11.如图,点A在反比例函数(k>0, x>0)的图象上,AB⊥y轴于点B,C为x轴正半轴上一点,将△ABC绕点A旋转180°得到△AED,点C的对应点D恰好落在函数图象上.若△BOC的面积为6,则k的值为___________.
12.如图1的螺丝钉由头部(直六棱柱)和螺纹(圆螺纹直径柱)组合而成,其俯视图如图2所示.小明想用一把刻度尺测量出螺纹直径.已知刻度尺紧靠螺纹,经过点A且交CD于点P,若测得AP长为13mm,正六边形ABCDEF的边长为7.5mm,则CP长为___________mm, 螺纹直径为___________mm.
13.满足不等式的负整数可以是______(写出一个即可).
14.若扇形的圆心角为,半径为6,则这个扇形的弧长为______(结果保留π).
15.在中,,,,D是射线AB上的一个动点,点E与点A关于直线CD对称,当______时,为直角三角形.
16.在中,,,为边的中点,以点为圆心,长为半径作弧,交直线于点,连结.则的度数是______.
三、解答题
17.如图,在平面直角坐标系中,过点、两点的抛物线的顶点C在x轴正半轴上.
(1)求抛物线的解析式;
(2)求点C的坐标;
(3)为线段AB上一点,,作轴交抛物线于点M,求PM的最大值与最小值.
18.定义:函数图像上到两坐标轴的距离都不大于的点叫做这个函数图像的“n阶方点”.例如,点是函数图像的“阶方点”;点是函数图像的“2阶方点”.
(1)在①;②;③三点中,是反比例函数图像的“1阶方点”的有___________(填序号);
(2)若y关于x的一次函数图像的“2阶方点”有且只有一个,求a的值;
(3)若y关于x的二次函数图像的“n阶方点”一定存在,请直接写出n的取值范围.
19.定义:有一个角为45°的平行四边形称为半矩形.
(1)如图1,若 ABCD的一组邻边AB=4,AD=7,且它的面积为14.求证: ABCD为半矩形.
(2)如图2,半矩形ABCD中,△ABD的外心O(外心O在△ABD内)到AB的距离为1,⊙O的半径=5,求AD的长.
(3)如图3,半矩形ABCD中,∠A=45°,AD=BD=4
①求证:CD是△ABD外接圆的切线;
②求出图中阴影部分的面积.
20.公路上正在行驶的甲车发现前方20m处沿同一方向行驶的乙车后,开始减速,减速后甲车行驶的路程s(单位:m)、速度v(单位:m/s)与时间t(单位:s)的关系分别可以用二次函数和一次函数表示,其图象如图所示.
(1)直接写出s关于t的函数关系式_____________和v关于t的函数关系式_____________(不要求写出t的取值范围)
(2)当甲车减速至9m/s时,它行驶的路程是多少?
(3)若乙车以10m/s的速度匀速行驶,两车何时相距最近,最近距离是多少?
21.如图,一次函数的图像与轴,轴分别交于,两点.
(1)求一次函数的解析式;
(2)若为轴上一动点,当的面积为6时,求点的坐标.
22.如图,将矩形ABCD沿AE折叠,使点D落在BC边的点F处.
(1)求证:△ABF∽△FCE;
(2)已知AB=3,AD=5,求的值.
23.某校积极落实“双减”政策,将要开设拓展课程,为让学生可以根据自己的兴趣爱好选择最喜欢的课程,进行问卷调查,问卷设置以下四种选项:A(综合模型)、B(摄影艺术)、C(音乐鉴赏)、D(劳动实践),随机抽取了部分学生进行调查,每名学生必须且只能选择其中最喜欢的一种课程,并将调查结果整理绘制成如下不完整的统计图.
根据以上信息,解答下列问题:
(1)此次被调查的学生人数为________名;
(2)直接在答题卡中补全条形统计图;
(3)求拓展课程D(劳动实践)所对应的扇形的圆心角的度数;
(4)根据抽样调查结果,请你估计该校800名学生中,有多少名学生最喜欢C(音乐鉴赏)拓展课程.
参考答案:
1.A
【分析】根据已知条件设,则,根据直径所对的圆周角是直角得出,根据同弧所对的圆周角相等得出,根据三角形内角和定理以及对顶角相等得出,根据等角对等边即可判断①,连接,证明,根据相似三角形的性质,即可得出②,从而求解.
【详解】解:如图所示,连接,
∵,设,则,
∵,
∴,
∵是直径,
∴,
在中,,
∴,
在中,,
,
∴,
∴;故①正确;
∵,
∴,
∴,
又,
∴,
∴,
即,
∴,故②正确,
故选:A.
【点睛】本题考查了同弧所对的圆周角相等,直径所对的圆周角是直角,相似三角形的性质与判定,等腰三角形的性质与判定,熟练掌握圆周角定理是解题的关键.
2.D
【分析】根据题意得到反比例函数式,再根据干比例函数式逐一进行判断即可得到答案.
【详解】解:由题意可知,压力一定时,压强和木板面积成反比,
人和木板对湿地地面的压力合为,
,
是S的反比例函数,
当S越来越大时,P也越来越小,
选项A不符合题意;
当S为时,,
选项B不符合题意;
压强P不超过,
,
,
S最少为,
选项C不符合题意,选项D符合题意,
故选D.
【点睛】本题考查了反比例函数的应用,根据题意写出反比例函数式是解题关键.
3.B
【分析】利用不等式的基本性质逐项判断即可.
【详解】解:A、由可得:,原变形正确,故此选项不符合题意;
B、由可得:,原变形错误,故此选项符合题意;
C、由可得:,原变形正确,故此选项不符合题意;
D、由可得:,原变形正确,故此选项不符合题意;
故选B.
【点睛】本题考查了不等式的性质,不等式的基本性质:①不等式的两边同时乘以(或除以)同一个正数,不等号的方向不变;②不等式的两边同时乘以(或除以)同一个负数,不等号的方向改变;③不等式的两边同时加上(或减去)同一个数或同一个含有字母的式子,不等号的方向不变.
4.A
【分析】根据轴对称图形的定义判断选择即可.
【详解】解:A选项是轴对称图形,符合题意;
B选项不是轴对称图形,不符合题意;
C选项不是轴对称图形,不符合题意;
D选项不是轴对称图形,不符合题意;
故选:A.
【点睛】本题考查了轴对称图形即沿着某条直线折叠,直线两旁的部分完全重合,熟练掌握定义是解题的关键.
5.C
【分析】根据函数图象的性质进行逐项分析即可.
【详解】解:由题中图象可知,该函数图象与x轴有三个交点,故②正确;
令,
解得:,,,
即该函数图象与x轴的三个交点坐标分别为,,,
∴结合图形可知,当时,y随x的增大而增大,故①正确;
∵自变量的范围是,
∴结合图象可知,当时,函数取得最大值,最大值为,
当时,函数取得最小值,最小值为,故③正确;
由图象可知,当时,函数图象在x轴上方的部分为或,
∴不等式的解为或,故④错误;
综上所述,正确的有①②③,共3个.
故选:C.
【点睛】本题考查函数图象的性质,掌握函数图象与坐标轴的交点的求法与意义,理解判断函数性质的方法是解题关键.
6.B
【分析】由题意知,,进而可得结果.
【详解】解:由题意知,,
故答案为:B.
【点睛】本题考查了二元一次方程组的应用.解题的关键在于根据题意正确的列方程组.
7.D
【分析】先根据等腰三角形的性质与判定得出,,,再根据平角定义得到和的关系式,根据三角形内角和得到和的关系式,结合求解即可.
【详解】解:∵,
∴,
∵,
∴,
∴,
∴,
又∵,
∴,即,
故选:D.
【点睛】本题考查了等腰三角形的性质与判定,三角形内角和定理和平角定义,熟练掌握相关知识点是解题的关键.
8.D
【分析】分别根据同底数幂的乘除法运算法则、合并同类项、幂的乘方运算法则逐项排查即可.
【详解】解:A. ,所以本选项计算错误,不符合题意;
B. ,所以本选项计算错误,不符合题意;
C.,所以本选项计算错误,不符合题意;
D.,所以本选项计算正确,符合题意.
故选:D.
【点睛】本题主要考查了同底数幂的乘法和除法、合并同类项、幂的乘方等知识点,灵活运用相关运算法则是解题的关键.
9.B
【分析】根据反比例函数图象上点的坐标特征,将点,,分别代入函数,求得的,然后比较它们的大小.
【详解】解:把,,分别代入:,
,
∵,
∴,
∴.
故选:B.
【点睛】本题考查的是反比例函数的性质,考查根据自变量的值判断函数值的大小,掌握判断方法是解题的关键.
10.B
【分析】根据中位数与众数的定义即可求解.中位数:把一组数据按从小到大的顺序排列,在中间的一个数字(或者两个数字的平均值)叫做这组数据的中位数.众数:在一组数据中出现次数最多的数.
【详解】解:将数据,,,,,,,
从小到大排列为:,,,,,,
∴众数为,中位数为,
故选:B.
【点睛】本题考查了中位数与众数的定义,熟练掌握中位数与众数的定义是解题的关键.
11.8
【分析】由旋转得到△ABC≌△AED,AC=AD,即点A为CD的中点,设B(0,m),则OB=m,通过面积表示C的坐标,进一步表示出A,D的坐标,将D代入反比例函数,求出k即可.
【详解】∵AB⊥y轴,OC⊥y轴,
∴AB∥OC,
∵△ABC绕点A旋转180°得到△AED,
∴△ABC≌△AED,
∴AC=AD,即点A为CD的中点,
设B(0,m),则OB=m,
∵,
∴,
∴C的坐标为,
∵点A在上,且AB⊥y轴,
∴A的纵坐标为m,
∴A ,
∵点A为CD的中点,
∴D,即,
∵D在上,∴,
∴4k-24=k,
∴k=8.
故答案为:8.
【点睛】本题考查了旋转和反比例函数的图象及性质,解题的关键是利用参数表示出图象上的点带入其表达式.
12. 0.5/ /
【分析】连接AC,过点B作BM⊥AC于点M,设正六边形ABCDEF的中心为O,连接AD,知A、O、D共线,过点O作ON⊥AP于点N,过D作DH⊥AP于H,利用正六边形的性质先、勾股定理求出AC的长度,结合AP的长度求出PC长度;再根据△AON∽△ADH知DH=2ON,设PH=x,利用勾股定理得到关于x的方程,再用勾股定理求出DH及ON长度即可.
【详解】解:连接AC,过点B作BM⊥AC于点M,设正六边形ABCDEF的中心为O,连接AD,由题意知,A、O、D共线,过点O作ON⊥AP于点N,过D作DH⊥AP于H,如图,
则,
由DH⊥AP知,ON∥DH,
∴△AON∽△ADH,
∴,
∵O是AD中点,
∴DH=2ON,
在正六边形ABCDEF中,mm,,
,,
在中,(mm),
(mm),
在中,mm,由勾股定理得,(mm),
∴DP=7mm,
∵正六边形的半径与边长相等,
mm,AD=15mm,
设PH=xmm,则AH=(13+x)mm,
在Rt△DPH和Rt△ADH中,由勾股定理得:
,
即,
即,
解得:x=,
∴DH=mm,
∴ON=mm,
故直径为
故答案为:0.5;.
【点睛】本题主要考查了正六边形的性质、勾股定理、相似三角形性质、解直角三角形以及等腰三角形的性质等知识点.解题关键是根据题意作出垂线,解直角三角形.
13.(答案不唯一)
【分析】先求出不等式的解集,再在解集中任选一个负整数即可.
【详解】解:解不等式得.
∴满足不等式的负整数可以是(答案不唯一).
故答案为:.
【点睛】本题考查求不等式的整数解,熟练掌握该知识点是解题关键.
14.
【分析】根据弧长的公式进行计算即可.
【详解】解:根据弧长的公式,
得到:.
故答案是:.
【点睛】本题主要考查了弧长的计算,熟记弧长公式是解题的关键.
15.0.8或5.6
【分析】由△ADE为等腰三角形,且为直角三角形,则只能∠ADE=90°,且△ADE为等腰直角三角形,
①D在A、B之间时,易证△BCG∽△BAC,得出,得出BG=1.8,利用勾股定理,得出DG=CG=2.4,进而得出AD的长;
②D在A、B之外时,易证△BCG∽△CAF,得出,令BG=3x,则CF=4x,进而表示出BD=,AD=5+,得出DF=,由GC=DF-DG-CF=,利用勾股定理GC2+BG2=BC2,求出x,进而得出AD的长.
【详解】解:∵∠ADE=90°,AD=DE,
∴△ADE为等腰直角三角形,
∴∠ADF=45°,
在中,,,,
∴AB==5,
①D在A、B之间时,
过点C作CG⊥AB于点G,
∴∠BGC=90°,
又∠ACB=90°,
∴△BCG∽△BAC,
∴,
又,,
∴BG=1.8,
在Rt△BCG中BG2+CG2=BC2,
∴1.82+CG2=32,
解得CG=2.4,
∵∠CDG=∠DCG=45°,
∴DG=CG=2.4,
∴AD=AB-DG-BG=5-2.4-1.8=0.8;
②D在A、B之外时,
过点B作BG⊥CD于点G,连接EC
∴∠BGC=90°,
∵点E与点A关于直线CD对称,
∴DF垂直平分AE,
∴∠AFD=90°,AD=DE,
又,
∵∠1+∠BCG=90°,∠2+∠BCG=90°,
∴∠1=∠2,
∴△BCG∽△CAF,
∴,
令BG=3x,则CF=4x,
∵BG⊥CD,
∴△BDG为等腰直角三角形,
∴BG=DG=3x,BD==,
∴AD=5+,
∴DF=,
∴GC=DF-DG-CF=,
在Rt△BCG中GC2+BG2=BC2,
∴()2+(3x)2=32
解得x1=, x2=,
∴当x1=时,GC=<0,
∴x=,
∴AD=5+=5.6.
综上可知,AD的长为0.8或5.6.
【点睛】本题考查轴对称的性质,勾股定理解直角三角形,相似三角形的判定和性质,等腰直角三角形的性质,熟练掌握以上内容是解决问题的关键.
16.25°或65°
【分析】根据等腰三角形的性质可以得到各内角的关系,然后根据题意,画出图形,利用分类讨论的方法求出的度数即可.
【详解】解:如图
,
,
为边的中点,
,,
当点在点的左侧时,
,,
,
;
当点在点的右侧时,
,,
,
,
的度数为 或.
故答案为: 或.
【点睛】本题主要考查等腰三角形的性质,圆的定义,解答本题的关键是画出合适的辅助线,利用分类讨论的方法解答.
17.(1)
(2)
(3)最大值是,最小值是4
【分析】(1)根据题意设抛物线的解析式为,然后把点、代入关系式进行计算即可解答;
(2)把代入(1)中所求的抛物线的解析式进行计算即可解答;
(3)先求出解析式,然后计算当,,,的长度,然后设,,表示出的值,然后再进行计算即可解答.
【详解】(1)解:∵抛物线的顶点在轴正半轴上,
∴设抛物线的解析式为,
把点、代入中可得:,
解得:舍去或,
∴,
∴抛物线的解析式为:;
(2)把代入中可得:,
∴,
∴点的坐标为;
(3)设的解析式为:,
把点、代入中可得:,
解得:,
∴的解析式为:,
∵点为线段上一点,点为抛物线上一点,且,轴,
∴当时,,,
∴,
当时,,,
∴,
当时,,,
∴,
设,,
∴,
当时,的最大值为:,
∴的最大值是,最小值是4.
【点睛】本题考查了二次函数的最值,待定系数法求二次函数解析式,二次函数的性质,二次函数图象上点的坐标特征,准确熟练地进行计算是解题的关键.
18.(1)②③
(2)3或;
(3)
【分析】(1)根据“n阶方点”的定义逐个判断即可;
(2)如图作正方形,然后分a>0和a<0两种情况,分别根据“2阶方点”有且只有一个判断出所经过的点的坐标,代入坐标求出a的值,并舍去不合题意的值即可得;
(3)由二次函数解析式可知其顶点坐标在直线y=-2x+1上移动,作出简图,由函数图象可知,当二次函数图象过点(n,-n)和点(-n, n)时为临界情况,求出此时n的值,由图象可得n的取值范围.
【详解】(1)解:∵点到x轴的距离为2,大于1,
∴不是反比例函数图象的“1阶方点”,
∵点和点都在反比例函数的图象上,且到两坐标轴的距离都不大于1,
∴和是反比例函数图象的“1阶方点”,
故答案为:②③;
(2)如图作正方形,四个顶点坐标分别为(2,2),(-2,2),(-2,-2),(2,-2),
当a>0时,若y关于x的一次函数图象的“2阶方点”有且只有一个,
则过点(-2,2)或(2,-2),
把(-2,2)代入得:,解得:(舍去);
把(2,-2)代入得:,解得:;
当a<0时,若y关于x的一次函数图象的“2阶方点”有且只有一个,
则过点(2,2)或(-2,-2),
把(2,2)代入得:,解得:;
把(-2,-2)代入得:,解得:(舍去);
综上,a的值为3或;
(3)∵二次函数图象的顶点坐标为(n,),
∴二次函数图象的顶点坐标在直线y=-2x+1上移动,
∵y关于x的二次函数图象的“n阶方点”一定存在,
∴二次函数的图象与以顶点坐标为(n,n),(-n,n),(-n,-n),(n,-n)的正方形有交点,
如图,当过点(n,-n)时,
将(n,-n)代入得:,
解得:,
当过点(-n,n)时,
将(-n,n)代入得:,
解得:或(舍去),
由图可知,若y关于x的二次函数图象的“n阶方点”一定存在,n的取值范围为:.
【点睛】本题考查了新定义,反比例函数图象上点的坐标特点,一次函数的图象和性质,二次函数的图象和性质,正确理解“n阶方点”的几何意义,熟练掌握数形结合思想的应用是解题的关键.
19.(1)见解析
(2)
(3)①见解析,②12﹣2π
【分析】(1)由S ABCD=AB DH=4×DH=14,解得DH=,进而求解;
(2)连接OD、OB、BD,则∠BDO=2∠DAB=90°,则BD=BO=5,进而求解;
(3)①证明△ABD为等腰直角三角形,得到OD是圆的半径且OD⊥CD,即可求解;
②由阴影部分的面积=S ABCD﹣S△ADO﹣S扇形ODB,即可求解.
【详解】(1)解:过点D作DH⊥AB交AB的延长线于点H,
∵S ABCD=AB DH=4×DH=14,解得DH=,
则AH==DH,
∴∠A=45°,
∴ ABCD为半矩形;
(2)解:连接OD、OB、BD,
则∠BDO=2∠DAB=90°,则BD=BO=5,
过点O作OH⊥AB于点H,则BH==AB,
则AB=4,
过点B作BE⊥AD于点E,
则BE=AB=4=AE,
在Rt△BDE中,DE=,
∴AD=AE+DE=4+;
(3)解:①过点D作DO⊥AB于点O,
∵∠A=45°,AD=BD=4,
故AB=4,则△ABD为等腰直角三角形,
则OD=AB=2,
∵ABCD,DO⊥AB,
∴OD⊥CD,
∴CD是△ABD外接圆的切线;
②阴影部分的面积=S ABCD﹣S△ADO﹣S扇形ODB
=4×2﹣×2×2﹣×π×(2)2
=12﹣2π.
【点睛】本题为圆的综合题,主要圆切线的判定与性质、新定义、平行四边形的性质、解直角三角形、面积的计算等,有一定的综合性,难度适中.
20.(1)s=﹣t2+16t,v=﹣t+16
(2)当甲车减速至9m/s时,它行驶的路程是87.5m
(3)6秒时两车相距最近,最近距离是2m
【分析】(1)根据图象信息,利用待定系数法分别求出一次函数和二次函数解析式即可;
(2)把代入一次函数解析式求出,再把的值代入二次函数解析式求出即可;
(3)根据当时,甲车的速度为16,当时,两车之间的距离逐渐变大,当时,两车之间的距离逐渐变小,得出当时,两车之间距离最小,代入计算即可.
【详解】(1)解:由图可知:二次函数图象经过原点,
设二次函数表达式为,一次函数表达式为,
二次函数经过,,
,解得:,
二次函数表达式为.
一次函数经过,,
,解得:,
一次函数表达式为.
故答案为:,;
(2)解:,
当时,
,解得,
,
当时,,
当甲车减速至9时,它行驶的路程是87.5;
(3)解:当时,甲车的速度为16,
当时,两车之间的距离逐渐变大,
当时,两车之间的距离逐渐变小,
当时,两车之间距离最小,
将代入中,得,
将代入中,得,
此时两车之间的距离为:,
秒时两车相距最近,最近距离是.
【点睛】本题考查了二次函数与一次函数的实际应用,解题的关键是理解题意,读懂函数图象,求出函数表达式.
21.(1)
(2)或
【分析】(1)待定系数法求解析式即可求解;
(2)设,根据的面积为6建立方程,解方程即可求解.
【详解】(1)解:∵一次函数的图像与轴,轴分别交于,两点,
∴,
解得,
一次函数的解析式为;
(2)解:设,
,,
,
当的面积为6时,,
解得或,
或.
【点睛】本题考查了待定系数法求一次函数解析式,三角形的面积,数形结合是解题的关键.
22.(1)见解析
(2)
【分析】(1)由折叠的性质得,进而得出,即可证明△ABF∽△FCE;
(2)设,则,由折叠的性质知,,,利用勾股定理求出BF,进而求出CF,在△CEF中根据勾股定理列方程求出x,则.
【详解】(1)证明:∵四边形ABCD是矩形,
∴,
由折叠的性质知,,
∴,,
∴.
在△ABF和△FCE中,
,
∴△ABF∽△FCE;
(2)解:∵矩形ABCD中,AB=3,AD=5,
∴,,
设,则,
由折叠的性质知,,,
由勾股定理得,,
∴,
在△CEF中,由勾股定理得:,
即,
解得,
∴,
∴.
【点睛】本题考查矩形的性质,折叠的性质,相似三角形的判定,勾股定理,三角函数解直角三角形等知识点,利用折叠的性质得出,,是解题的关键.
23.(1)120
(2)见解析
(3)72
(4)320名
【分析】(1)先求出B的人数,再将各项人数相加即可.
(2)见解析
(3)根据D的百分比乘以圆心角即可.
(4)求出C所占的百分比,乘以800.
【详解】(1)解:根据扇形统计图中,B是A的3倍
故喜欢B的学生数为(名)
统计调查的总人数有:12+36+48+24=120(名).
(2)
(3)由条形统计图可知:
D的人数是A的2倍,故D占总人数的20%
所以D所占圆心角为20%
答:课程D所对应的扇形的圆心角的度数为72.
(4)若有800名学生,则喜欢C的学生数有:
(名)
答:有320名学生最喜欢C拓展课程.
【点睛】本题考查扇形统计图与条形统计图相关内容,注意从图中获取信息,分析图中数据之间的数量关系是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
