【考前必刷】浙江地区2023年中考数学全真模拟卷12(含解析)
文档属性
| 名称 | 【考前必刷】浙江地区2023年中考数学全真模拟卷12(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-03 22:28:09 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
【考前必刷】浙江地区中考数学全真模拟卷12
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.某学校计划购买甲、乙两种品牌的电子白板共40台.甲、乙两种品牌电子白板的单价分别为2.5万元/台和1.5万元/台,若购买甲品牌电子白板费用为万元,则购买乙品牌电子白板费用为( )
A.万元 B.万元 C.万元 D.万元
2.已知点,,都在抛物线上,,点,在对称轴的两侧,下列选项正确的是( )
A.若,则 B.若,则
C.若,则 D.若,则
3.用代入法解二元一次方程组时,将方程①代入方程②,得到结果正确的是( )
A. B. C. D.
4.城市书房有一群学生在看书,现统计他们的年龄如下表.他们年龄的中位数为( )
人数(人) 2 3 8 2
年龄(岁) 11 12 13 14
A.11岁 B.12岁 C.岁 D.13岁
5.一个不透明的袋中装有11个只有颜色不同的球,其中4个白球,5个红球,2个黄球.从中任意摸出1个球是红球的概率为( )
A. B. C. D.
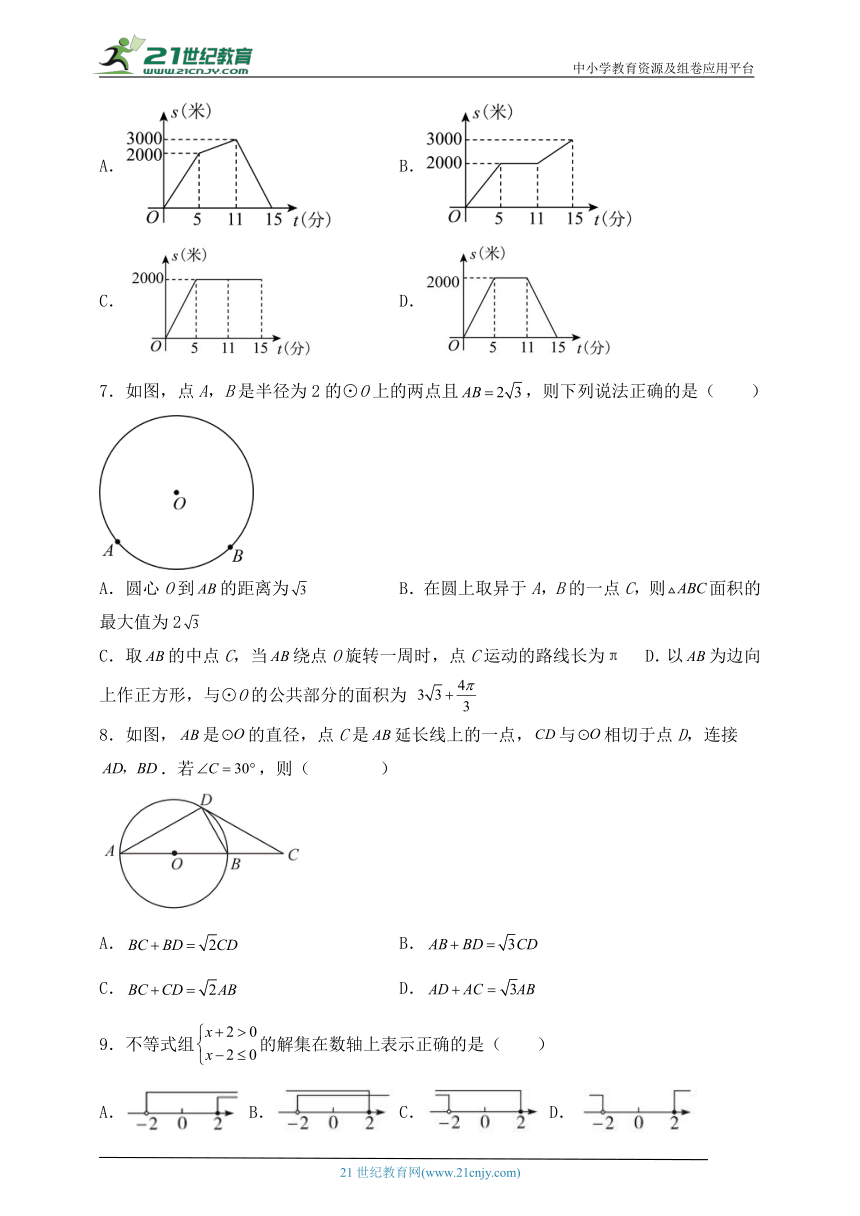
6.小刚从家里出发,以400米/分钟的速度匀速骑车5分钟后就地休息了6分钟,然后以500米/分钟的速度匀速骑回家里掎回家里.表示离家路程,表示骑行时间,下列函数图象能表达这一过程的是( )
A. B.
C. D.
7.如图,点A,B是半径为2的⊙O上的两点且,则下列说法正确的是( )
A.圆心O到的距离为 B.在圆上取异于A,B的一点C,则面积的最大值为2
C.取的中点C,当绕点O旋转一周时,点C运动的路线长为π D.以为边向上作正方形,与⊙O的公共部分的面积为
8.如图,是的直径,点C是延长线上的一点,与相切于点D,连接.若,则( )
A. B.
C. D.
9.不等式组的解集在数轴上表示正确的是( )
A. B. C. D.
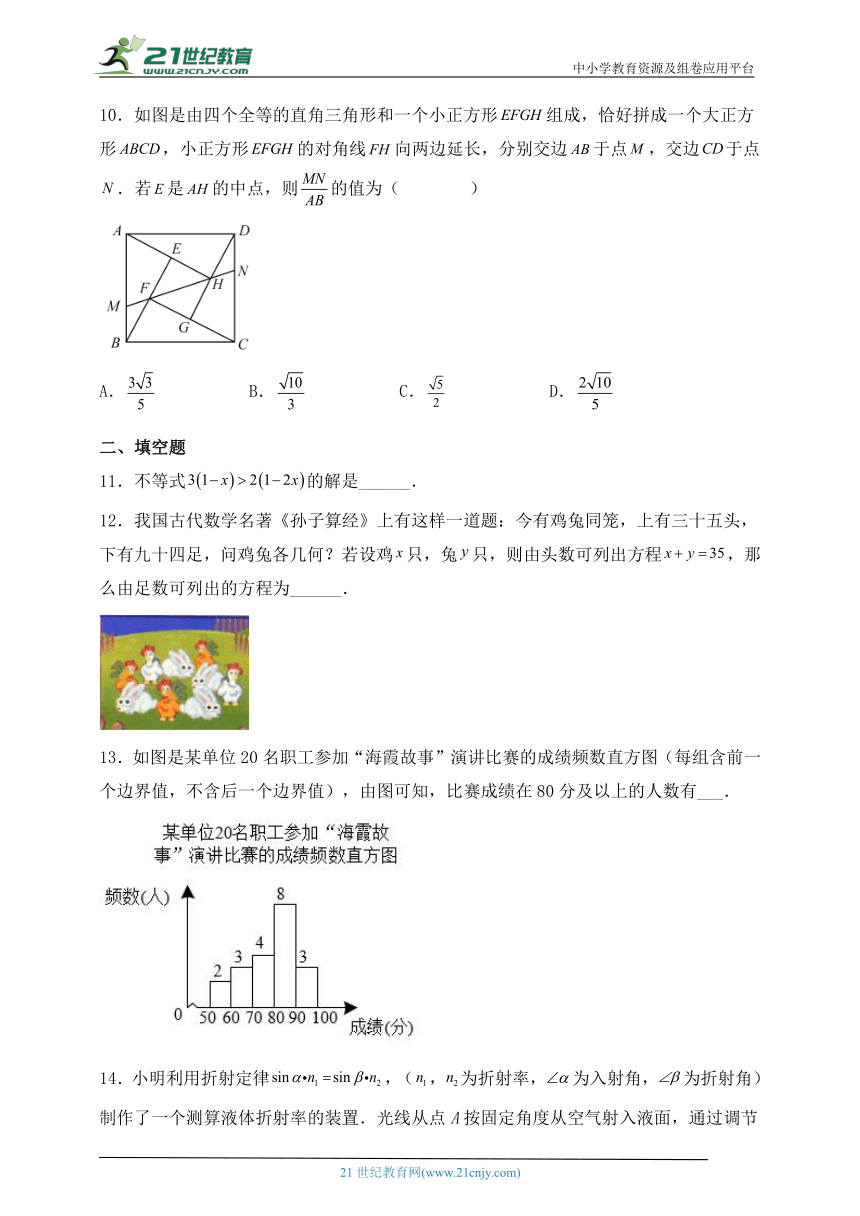
10.如图是由四个全等的直角三角形和一个小正方形组成,恰好拼成一个大正方形,小正方形的对角线向两边延长,分别交边于点,交边于点.若是的中点,则的值为( )
A. B. C. D.
二、填空题
11.不等式的解是______.
12.我国古代数学名著《孙子算经》上有这样一道题:今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔各几何?若设鸡只,兔只,则由头数可列出方程,那么由足数可列出的方程为______.
13.如图是某单位20名职工参加“海霞故事”演讲比赛的成绩频数直方图(每组含前一个边界值,不含后一个边界值),由图可知,比赛成绩在80分及以上的人数有___.
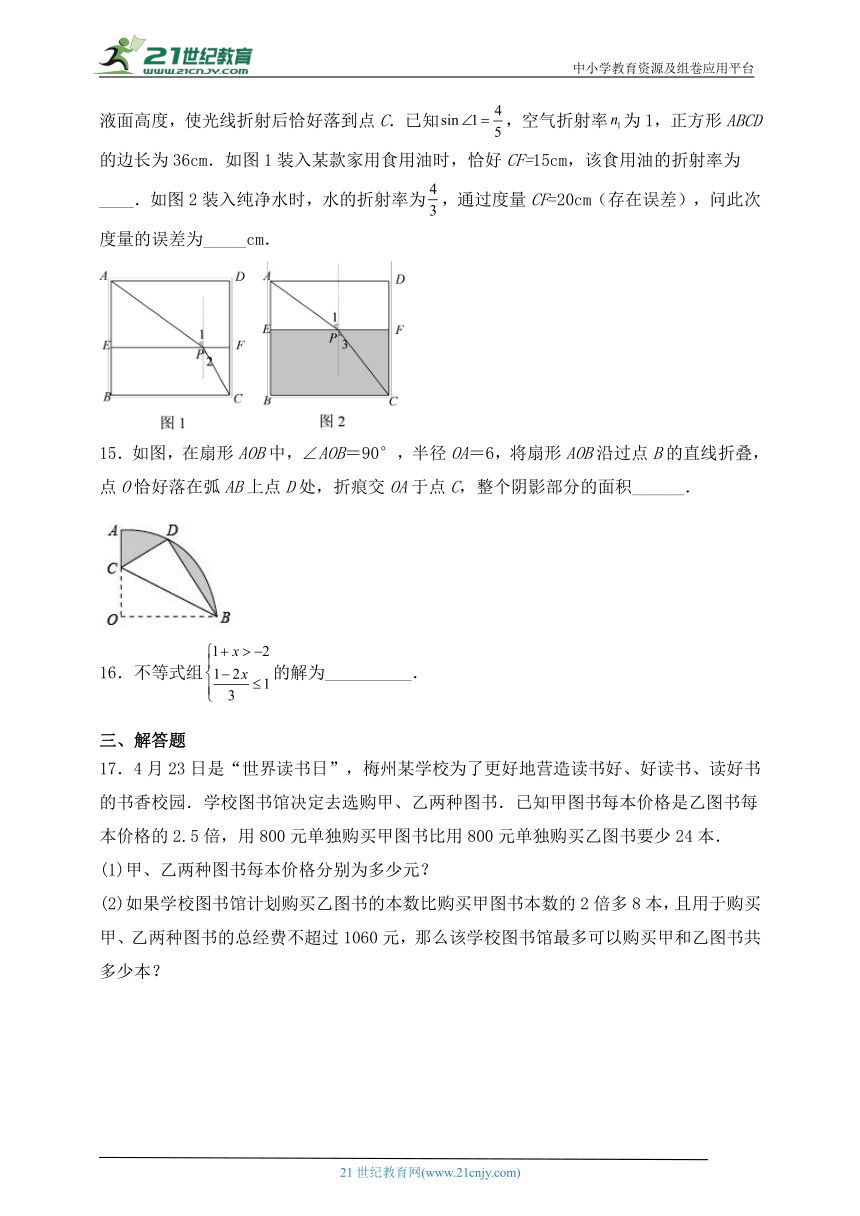
14.小明利用折射定律,(,为折射率,为入射角,为折射角)制作了一个测算液体折射率的装置.光线从点A按固定角度从空气射入液面,通过调节液面高度,使光线折射后恰好落到点C.已知,空气折射率为1,正方形ABCD的边长为36cm.如图1装入某款家用食用油时,恰好CF=15cm,该食用油的折射率为____.如图2装入纯净水时,水的折射率为,通过度量CF=20cm(存在误差),问此次度量的误差为_____cm.
15.如图,在扇形AOB中,∠AOB=90°,半径OA=6,将扇形AOB沿过点B的直线折叠,点O恰好落在弧AB上点D处,折痕交OA于点C,整个阴影部分的面积______.
16.不等式组的解为__________.
三、解答题
17.4月23日是“世界读书日”,梅州某学校为了更好地营造读书好、好读书、读好书的书香校园.学校图书馆决定去选购甲、乙两种图书.已知甲图书每本价格是乙图书每本价格的2.5倍,用800元单独购买甲图书比用800元单独购买乙图书要少24本.
(1)甲、乙两种图书每本价格分别为多少元?
(2)如果学校图书馆计划购买乙图书的本数比购买甲图书本数的2倍多8本,且用于购买甲、乙两种图书的总经费不超过1060元,那么该学校图书馆最多可以购买甲和乙图书共多少本?
18.织里童装城某拉链专卖店出售甲、乙两种拉链,已知该店进货甲种拉链100条和乙种拉链60条共需280元,进货甲种拉链160条和乙种拉链100条共需456元.
(1)求出甲、乙两种拉链的进价;
(2)已知专卖店将甲种拉链提价0.4元出售,乙种拉链提价25%出售.小明在该专卖店购买甲、乙两种拉链,共花费45元,求有哪几种购买方案;
(3)在(2)条件下,不同方案专卖店获利是否发生变化,如果变化,请求出最大值;如果不变,请说明理由.
计算:﹣110+|2﹣(﹣3)2|+÷(﹣).
20.如图,在中,AD平分,过点B作AD的垂线,垂足为点D,,交AB于点E,.
(1)求证:是等腰三角形;
(2)求证:.
21.如图,抛物线(a>0)交x轴于点A(﹣1,0),B(3,0),交y轴于点C,作直线BC.
(1)若OB=OC,求抛物线的表达式;
(2)P是线段BC下方抛物线上一个动点,过点P作PF⊥x轴于点F,交线段BC于点E.若EB=EC=EP,求a的值.
22.如图,△ABC中,CA=CB,以BC为直径的⊙O与底边AB交于点D,过D点作⊙O的切线DE,交AC于点E.
(1)证明:DE⊥AC;
(2)连接OE,当,S△OCE=6时,求⊙O的半径.
23.如图,已知⊙C过菱形ABCD的三个顶点B,A,D,连结BD,过点A作AEBD交射线CB于点E.
(1)求证:AE是⊙C的切线.
(2)若半径为2,求图中阴影部分的面积.
(3)在(2)的条件下,在⊙C上取点F,连结AF,使∠DAF=15°,求点F到直线AD的距离.
参考答案:
1.A
【分析】根据购买甲品牌电子白板费用为万元可得购买甲品牌电子白板台,可求出购买乙品牌电子白板的数量为台,再根据“单价×数量”可得结论.
【详解】解:∵甲品牌电子白板的单价分别为2.5万元/台,且购买甲品牌电子白板费用为万元,
∴购买甲品牌电子白板台,
∴购买乙品牌电子白板的数量为台,
∴购买乙品牌电子白板费用为万元
故选:A
【点睛】本题主要考查了列代数式,理解题意是解答本题的关键.
2.C
【分析】根据题目中的抛物线和二次函数的性质,可以判断当时,、的大小关系或当时,、的大小关系.
【详解】解:抛物线,
该抛物线的对称轴为直线,抛物线开口向上,当时,随的增大而增大,当时,随的增大而减小,
点,,都在抛物线上,点在点左侧,
若,则,故选项、均不符合题意;
若,则,故选项符合题意,选项不符合题意;
故选: .
【点睛】本题考查二次函数图象上点的坐标特征,解答本题的关键是明确题意,利用二次函数的性质解答.
3.B
【分析】方程组利用代入消元法变形得到结果,即可作出判断.
【详解】解:用代入法解二元一次方程组时,将方程①代入方程②,得:,
故选:B.
【点睛】此题考查了解二元一次方程组,熟练掌握运算法则是解本题的关键.
4.D
【分析】根据中位数的定义,把这组数据从小到大排列找出最中间的数即可.
【详解】解:这组年龄数据共有15个数,
他们年龄的中位数是第8个数,
把这组数据从小到大排列,第8个数是13岁,
他们年龄的中位数为13岁,
故选:D.
【点睛】本题考查了中位数,熟记中位数的定义是解题关键.
5.D
【分析】利用红球的个数除以球的总个数解答即可.
【详解】解:一个不透明的布袋里装有11个有颜色不同的球,从布袋里任意摸出1个球,所有可能一共有11种情况,
其中红球有5个,从布袋里任意摸出1个球,红球出现的可能情况只有5种,
从布袋里任意摸出1个球,是红球的概率为.
故选:D.
【点睛】本题考查了简单事件的概率,属于基础题型,熟知概率的计算方法是解题关键.
6.D
【分析】因为小刚以400米/分的速度匀速骑车5分,可求其行驶的路程对照排除错误选项,“在原地休息”对应在图象上表示时间在增加,而距离不变,即这一线段与x轴平行,“回到原出发地”表示终点的纵坐标为0,综合分析选出正确答案.
【详解】解:∵(米)=2(千米),
∴小刚以400米/分的速度匀速骑车5分行驶的路程为2千米,
而选项A与B中纵轴表示速度,且速度为变量,这与事实不符,故排除选项A与B,
又∵“回到原出发地”表示终点的纵坐标为0,
∴排除选项C,
故选:D.
【点睛】本题考查了函数的图象,解题的关键是理解函数图象的意义.
7.D
【分析】由垂径定理,勾股定理求出,延长交圆于,即可求出的最大面积,当绕点旋转一周时,点运动的路线是以为圆心半径是1的圆,即可求出运动的路线长,以为边向上作正方形,与的公共部分的面积扇形的面积+的面积,于是可以得到答案.
【详解】解:如图①,于,
,
,
,
故A不符合题意;
如图①延长交圆于,此时的面积最大,
,,
的面积,
故B不符合题意;
取的中点,连接,,,
,
,
,
当绕点旋转一周时,点运动的路线是以为圆心半径是1的圆,
运动的路线长是,
故C不符合题意;
如图②四边形是正方形,连接,,则过圆心O,作于,
的面积,
,
的面积的面积的面积,
,
扇形的面积,
以为边向上作正方形,与的公共部分的面积扇形的面积的面积,
故D符合题意.
故选:D.
【点睛】本题考查扇形面积的计算,三角形面积的计算,垂径定理,勾股定理,掌握以上知识点是解题的关键.
8.B
【分析】连接.根据切线的性质可得出,根据直径所对圆周角为直角得出,结合题意易证为等边三角形,最后由含30度角的直角三角形的性质结合勾股定理逐项计算判断即可.
【详解】解:如图,连接.
∵与相切于点D,
∴.
∵,
∴,,
∴,即.
∵,
∴为等边三角形,
∴,
∴,故A错误,不符合题意;
∵,,
∴,
∴,故B正确,符合题意;
∵,,
∴.
∵,
∴,
∴.
∵,
∴,故C错误,不符合题意;
∵是的直径,
∴.
∵为等边三角形,
∴,
∴,
∴,
∴,
∴,
∴,故D错误,不符合题意.
故选B.
【点睛】本题考查切线的性质,圆周角定理的推论,等边三角形的判定和性质,含30度角的直角三角形的性质以及勾股定理.连接常用的辅助线是解题关键.
9.B
【分析】此题考查一元一次不等式组的解法以及解集在数轴上的表示,如果带等号用实心表示,如果不带等号用空心表示.
【详解】解:此题考查一元一次不等式组的解法以及解集在数轴上的表示,如果带等号用实心表示,如果不带等号用空心表示;
,当;
当;
当;
当解集不存在;
分别对应下图中的图;
此题中原不等式组可以化为:,所以由图可知,故选B.
【点睛】本题考查不等式解集在数轴上的表示,掌握方法是关键.
10.B
【分析】根据正方形的性质得到,,再利用锐角三角形函数得到,最后根据勾股定理及全等三角形判定与性质即可解答.
【详解】解:过点作于点,设,
∵是的中点,
∴,
∴,
∵在正方形中,
∴,
∵,
∴设,
∴,
∵,
∴,
∴,
∴,
∴,
∴在中,,
∵正方形是由四个全等的直角三角形和一个小正方形组成,
∴,
∴,
∵在和中,
,
∴,
∴,
∵在中,,
∴,
∴,
故选.
【点睛】本题考查了正方形的性质,全等三角形的判定与性质,勾股定理,锐角三角形函数,掌握锐角三角形函数是解题的关键.
11.
【分析】去括号,根据不等式的性质即可求解.
【详解】解
3-3x>2-4x
-3x+4x>2-3
x>-1
故答案为:.
【点睛】此题主要考查解一元一次不等式,解题的关键是熟知不等式的性质.
12.
【分析】根据题意得x只鸡的足数+y只兔的足数=94,再根据等量关系列出方程即可.
【详解】根据题意,得
2x+4y=94.
故答案为:2x+4y=94.
【点睛】本题主要考查了列二元一次方程组,确定等量关系是列方程的关键.
13.11
【分析】根据成绩频数直方图中各组频数进行计算即可.
【详解】解:由直方图知,成绩在80分及以上的人数共有:8+3=11人,
故答案为:11.
【点睛】本题考查了频数分布直方图,从频数分布直方图中得到各组频数是解题关键.
14. 1.7
【分析】设EP=4x,则AP=5x,AE=3x,得到PF=36-4x,CF=36-3x,图1中由CF=15求出x=7,得到CP=17,表示出sin∠2的值,由此求出折射率n2;图2中由水的折射率为,即,求出sin∠3,得到,列得,解得x由此得到答案.
【详解】解:∵∠1=∠EAP,,
∴,
设EP=4x,则AP=5x,AE=3x,
图1中PF=36-4x,CF=36-3x,
∴36-3x=15,
解得x=7,
∴PF=36-4x=8,
∴CP=17,
∴,
∵,
∴,
∴;
图2,∵水的折射率为,即,
∴,
∴,
∴,
∴,
解得x=,
∴,
∴误差为,
故答案为:1.7;.
【点睛】此题考查了正方形的性质,三角函数问题,正确理解题意及掌握相应的物理知识是解题的关键.
15.
【分析】首先连接OD,由折叠的性质,可得CD=CO,BD=BO,∠DBC=∠OBC,则可得△OBD是等边三角形,继而求得OC的长,即可求得△OBC与△BCD的面积,又在扇形OAB中,∠AOB=90°,半径OA=6,即可求得扇形OAB的面积,继而求得阴影部分面积.
【详解】解:如图,连接OD,
根据折叠的性质,CD=CO,BD=BO,∠DBC=∠OBC,
∴OB=OD=BD,
即△OBD是等边三角形,
∴∠DBO=60°,
∴∠CBO=∠DBO=30°,
∵∠AOB=90°,
∴OC=OB tan∠CBO=6,
∴S△BDC=S△OBC=×OB×OC=×6×=6,
S扇形AOB=π×62=9π,
∴整个阴影部分的面积为:S扇形AOB-S△BDC-S△OBC=9π-6-6=9π-12,
故答案为:.
【点睛】本题考查了折叠的性质、扇形面积公式以及直角三角形的性质.此题难度适中,注意数形结合思想的应用,注意辅助线的作法.
16.
【分析】分别求出不等式,得到不等式的解集即可;
【详解】解:解得:
解得:
故不等式的解集为:
故答案为:
【点睛】本题主要考查不等式组解集的求解,掌握不等式组解集的求解方法是解题的关键.
17.(1)甲图书每本价格是50元,乙图书每本价格为20元
(2)该学校图书馆最多可以购买甲和乙图书共38本
【分析】(1)设乙图书每本价格为x元,则甲图书每本价格是2.5x元,由题意:用800元单独购买甲图书比用800元单独购买乙图书要少24本,列出分式方程,解方程即可;
(2)设购买甲种图书a本,则购买乙种图书(2a+8)本,由题意:用于购买甲、乙两种图书的总经费不超过1060元,列出一元一次不等式,解不等式,进而得出结论.
【详解】(1)设乙图书每本价格为x元,则甲图书每本价格是2.5x元,
根据题意得:,
解得:x=20,
经检验:x=20是原方程的根,
则2.5x=50,
答:甲图书每本价格是50元,乙图书每本价格为20元;
(2)设购买甲种图书a本,则购买乙种图书(2a+8)本,
由题意得:50a+20(2a+8)≤1060,
解得:a≤10,
∴2a+8≤28, 则10+28=38,
答:该学校图书馆最多可以购买甲和乙图书共38本.
【点睛】本题考查了分式方程的应用以及一元一次不等式的应用,解题的关键是:(1)找准等量关系,正确列出分式方程;(2)找出数量关系,正确列出一元一次不等式.
18.(1)甲种拉链的进价为1.6元,乙种拉链的进价为2元
(2)有4种购买方案:①甲种拉链5条,乙种拉链14条;②甲种拉链10条,乙种拉链10条;③甲种拉链15条,乙种拉链6条;④甲种拉链20条,乙种拉链2条
(3)不发生变化,理由见解析
【解析】(1)解:设甲种拉链的进价为每条x元,乙种拉链的进价为每条y元,由题意得:,解得:,答:甲种拉链的进价为1.6元,乙种拉链的进价为2元.
(2)解:设购买甲种拉链m条,乙种拉链n条,由题意得:(1.6+0.4)m+2(1+25%)n=45,整理得:n=18﹣m,∵m、n为正整数,∴或或或,即有4种购买方案:①甲种拉链5条,乙种拉链14条;②甲种拉链10条,乙种拉链10条;③甲种拉链15条,乙种拉链6条;④甲种拉链20条,乙种拉链2条.
(3)解:不发生变化,理由如下:∵利润w=0.4m+2×25%×(18﹣m)=9(元),∴不同方案专卖店获利不发生变化.
【点睛】此题考查了二元一次方程组的应用、二元一次方程的应用,读懂题意,找到等量关系,列出二元一次方程组或二元一次方程是解题的关键.
19.
【分析】先计算乘方及绝对值运算,再计算除法运算,最后算算加减运算即可求出值.
【详解】解:原式=﹣1+|2﹣9|+×(﹣)
=﹣1+7﹣
=6﹣
=
【点睛】本题主要考查了有理数的混合运算,熟练掌握有理数的混合运算法则是解题的关键.
20.(1)证明见解析;
(2)证明见解析
【详解】(1)证明:如图,∵AD平分∠BAC,
∴∠1=∠2,
∵,CD∥AB,
∴.
∵,,
∴,
∴,
∴是等腰三角形;
(2)证明:由(1)得
∴,
∵,,,
∴,
∴,
∴.
【点睛】本题考查了等腰三角形的判定与性质、平行线的性质及全等三角形的判定与性质,熟练掌握等腰三角形的判定与性质是解题的关键.
21.(1)
(2)
【分析】(1)由OB=OC得出C的坐标,再利用待定系数法即可得出结论;
(2)先根据BE=EC求出点E的坐标,再求出BE的长度,把P的坐标用含a的式子表示出来,根据EB=EP即可得出答案.
【详解】(1)解:∵OB=OC,
∴C(0,﹣3),
把A,B,C代入中,
得:,
解得:,
∴抛物线的解析式为;
(2)解:如图,连接BC,
∵EB=EC,
∴E是BC的中点,
∴E的坐标为(,),
∴P的横坐标为,
把A,B代入中,
得:,
解得:,
∴抛物线的解析式为,
把x=代入,得y=,
∴P(,),
∴EP==,
解得a=,
∴a的值为.
【点睛】本题主要考查二次函数的图象与性质,解题的关键是要会用待定系数法求抛物线的解析式,牢记勾股定理的公式.
22.(1)见解析
(2)
【分析】(1)连接OD,根据DE是⊙O的切线,可得∠ODE=90°,由AC=BC,可得∠OBD=∠A,进而可得∠A=∠ODB,可得ODAC,即可证明结论;
(2)连接CD,证明∠CDE=∠ABC,由得,设CE=3x,CD=5x,则DE=4x,根据S△OCE=6可求出x的值,可得CD的长,由可得BC的长,即可得⊙O的半径.
【详解】(1)证明:如图1,连接OD,则OD为⊙O的半径,
∵DE是⊙O的切线,
∴∠ODE=90°,
∵OB=OD,
∴∠OBD=∠ODB,
∵AC=BC,
∴∠OBD=∠A,
∴∠A=∠ODB,
∴ODAC,
∴∠DEC=180°-∠ODE=90°,
∴DE⊥AC;
(2)解:连接CD,如图2,
∵BC为直径,
∴∠BDC=∠CDA=90°,
∴∠CDE+∠EDA=90°,
∵DE⊥AC,
∴∠ADE+∠A=90°,
∴∠A=∠CDE,
∵CA=CB,
∴∠A=∠B,
∴∠CDE=∠ABC,
∴,
设CE=3x,CD=5x,则DE==4x,
∵S△OCE=CE DE=6=6,
∴x=1或x=﹣1(不合题意,舍去),
∴x=1,
∴CD=5,
∵,
∴BC=,
∴⊙O的半径为.
【点睛】此题主要考查了圆的切线的性质定理、圆周角定理、锐角三角函数、勾股定理、等腰三角形的判定和性质等知识,熟练掌握锐角三角函数的定义是解题的关键.
23.(1)见解析
(2)
(3)2-或-1
【分析】(1)连接AC.证明AE⊥AC即可解决问题.
(2)证明△ABC是等边三角形,推出∠ACB=60°,AE=AC tan60°=2,根据求解即可.
(3)分两种情形:①如图2中,当点F在上时.②如图3中,当点F在优弧上时,分别求解即可.
【详解】(1)证明:如图1中,连接AC,
∵四边形ABCD是菱形,
∴AC⊥BD,
又∵BDAE,
∴AC⊥AE,
∴AE是⊙O的切线.
(2)解:如图1中,
∵四边形ABCD是菱形,
∴AB=BC,
又∵AC=BC,
∴△ABC是等边三角形,
∴∠ACB=60°,
∵AC=2,
∴AE=AC tan60°=2,
∴
=
=.
(3)解:分两种情形:①如图2中,当点F在上时,
∵∠DAF=15°,
∴∠DCF=30°,
∵∠ACD=60°,
∴∠ACF=∠FCD,
∴点F是弧AD的中点,
∴CF⊥AD,
∴点F到直线AD的距离=CF-CA cos30°=2-.
②如图3中,当点F在优弧上时,
∵∠DAF=15°,
∴∠DCF=30°,
过点C作CG⊥AD于G,过点F作FH⊥CG于H,
可得∠AFH=15°,∠HFC=30°,
∴CH=1,
∴点F到直线AD的距离=CG-CH=AC cos30°-CH=-1.
综上所述,满足条件的点F到直线AD的距离为2-或-1.
【点睛】本题属于圆综合题,考查了切线的判定,菱形的性质,等边三角形的判定和性质,解直角三角形等知识,解题的关键是学会用分类讨论的思想思考问题,属于中考压轴题.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
【考前必刷】浙江地区中考数学全真模拟卷12
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.某学校计划购买甲、乙两种品牌的电子白板共40台.甲、乙两种品牌电子白板的单价分别为2.5万元/台和1.5万元/台,若购买甲品牌电子白板费用为万元,则购买乙品牌电子白板费用为( )
A.万元 B.万元 C.万元 D.万元
2.已知点,,都在抛物线上,,点,在对称轴的两侧,下列选项正确的是( )
A.若,则 B.若,则
C.若,则 D.若,则
3.用代入法解二元一次方程组时,将方程①代入方程②,得到结果正确的是( )
A. B. C. D.
4.城市书房有一群学生在看书,现统计他们的年龄如下表.他们年龄的中位数为( )
人数(人) 2 3 8 2
年龄(岁) 11 12 13 14
A.11岁 B.12岁 C.岁 D.13岁
5.一个不透明的袋中装有11个只有颜色不同的球,其中4个白球,5个红球,2个黄球.从中任意摸出1个球是红球的概率为( )
A. B. C. D.
6.小刚从家里出发,以400米/分钟的速度匀速骑车5分钟后就地休息了6分钟,然后以500米/分钟的速度匀速骑回家里掎回家里.表示离家路程,表示骑行时间,下列函数图象能表达这一过程的是( )
A. B.
C. D.
7.如图,点A,B是半径为2的⊙O上的两点且,则下列说法正确的是( )
A.圆心O到的距离为 B.在圆上取异于A,B的一点C,则面积的最大值为2
C.取的中点C,当绕点O旋转一周时,点C运动的路线长为π D.以为边向上作正方形,与⊙O的公共部分的面积为
8.如图,是的直径,点C是延长线上的一点,与相切于点D,连接.若,则( )
A. B.
C. D.
9.不等式组的解集在数轴上表示正确的是( )
A. B. C. D.
10.如图是由四个全等的直角三角形和一个小正方形组成,恰好拼成一个大正方形,小正方形的对角线向两边延长,分别交边于点,交边于点.若是的中点,则的值为( )
A. B. C. D.
二、填空题
11.不等式的解是______.
12.我国古代数学名著《孙子算经》上有这样一道题:今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔各几何?若设鸡只,兔只,则由头数可列出方程,那么由足数可列出的方程为______.
13.如图是某单位20名职工参加“海霞故事”演讲比赛的成绩频数直方图(每组含前一个边界值,不含后一个边界值),由图可知,比赛成绩在80分及以上的人数有___.
14.小明利用折射定律,(,为折射率,为入射角,为折射角)制作了一个测算液体折射率的装置.光线从点A按固定角度从空气射入液面,通过调节液面高度,使光线折射后恰好落到点C.已知,空气折射率为1,正方形ABCD的边长为36cm.如图1装入某款家用食用油时,恰好CF=15cm,该食用油的折射率为____.如图2装入纯净水时,水的折射率为,通过度量CF=20cm(存在误差),问此次度量的误差为_____cm.
15.如图,在扇形AOB中,∠AOB=90°,半径OA=6,将扇形AOB沿过点B的直线折叠,点O恰好落在弧AB上点D处,折痕交OA于点C,整个阴影部分的面积______.
16.不等式组的解为__________.
三、解答题
17.4月23日是“世界读书日”,梅州某学校为了更好地营造读书好、好读书、读好书的书香校园.学校图书馆决定去选购甲、乙两种图书.已知甲图书每本价格是乙图书每本价格的2.5倍,用800元单独购买甲图书比用800元单独购买乙图书要少24本.
(1)甲、乙两种图书每本价格分别为多少元?
(2)如果学校图书馆计划购买乙图书的本数比购买甲图书本数的2倍多8本,且用于购买甲、乙两种图书的总经费不超过1060元,那么该学校图书馆最多可以购买甲和乙图书共多少本?
18.织里童装城某拉链专卖店出售甲、乙两种拉链,已知该店进货甲种拉链100条和乙种拉链60条共需280元,进货甲种拉链160条和乙种拉链100条共需456元.
(1)求出甲、乙两种拉链的进价;
(2)已知专卖店将甲种拉链提价0.4元出售,乙种拉链提价25%出售.小明在该专卖店购买甲、乙两种拉链,共花费45元,求有哪几种购买方案;
(3)在(2)条件下,不同方案专卖店获利是否发生变化,如果变化,请求出最大值;如果不变,请说明理由.
计算:﹣110+|2﹣(﹣3)2|+÷(﹣).
20.如图,在中,AD平分,过点B作AD的垂线,垂足为点D,,交AB于点E,.
(1)求证:是等腰三角形;
(2)求证:.
21.如图,抛物线(a>0)交x轴于点A(﹣1,0),B(3,0),交y轴于点C,作直线BC.
(1)若OB=OC,求抛物线的表达式;
(2)P是线段BC下方抛物线上一个动点,过点P作PF⊥x轴于点F,交线段BC于点E.若EB=EC=EP,求a的值.
22.如图,△ABC中,CA=CB,以BC为直径的⊙O与底边AB交于点D,过D点作⊙O的切线DE,交AC于点E.
(1)证明:DE⊥AC;
(2)连接OE,当,S△OCE=6时,求⊙O的半径.
23.如图,已知⊙C过菱形ABCD的三个顶点B,A,D,连结BD,过点A作AEBD交射线CB于点E.
(1)求证:AE是⊙C的切线.
(2)若半径为2,求图中阴影部分的面积.
(3)在(2)的条件下,在⊙C上取点F,连结AF,使∠DAF=15°,求点F到直线AD的距离.
参考答案:
1.A
【分析】根据购买甲品牌电子白板费用为万元可得购买甲品牌电子白板台,可求出购买乙品牌电子白板的数量为台,再根据“单价×数量”可得结论.
【详解】解:∵甲品牌电子白板的单价分别为2.5万元/台,且购买甲品牌电子白板费用为万元,
∴购买甲品牌电子白板台,
∴购买乙品牌电子白板的数量为台,
∴购买乙品牌电子白板费用为万元
故选:A
【点睛】本题主要考查了列代数式,理解题意是解答本题的关键.
2.C
【分析】根据题目中的抛物线和二次函数的性质,可以判断当时,、的大小关系或当时,、的大小关系.
【详解】解:抛物线,
该抛物线的对称轴为直线,抛物线开口向上,当时,随的增大而增大,当时,随的增大而减小,
点,,都在抛物线上,点在点左侧,
若,则,故选项、均不符合题意;
若,则,故选项符合题意,选项不符合题意;
故选: .
【点睛】本题考查二次函数图象上点的坐标特征,解答本题的关键是明确题意,利用二次函数的性质解答.
3.B
【分析】方程组利用代入消元法变形得到结果,即可作出判断.
【详解】解:用代入法解二元一次方程组时,将方程①代入方程②,得:,
故选:B.
【点睛】此题考查了解二元一次方程组,熟练掌握运算法则是解本题的关键.
4.D
【分析】根据中位数的定义,把这组数据从小到大排列找出最中间的数即可.
【详解】解:这组年龄数据共有15个数,
他们年龄的中位数是第8个数,
把这组数据从小到大排列,第8个数是13岁,
他们年龄的中位数为13岁,
故选:D.
【点睛】本题考查了中位数,熟记中位数的定义是解题关键.
5.D
【分析】利用红球的个数除以球的总个数解答即可.
【详解】解:一个不透明的布袋里装有11个有颜色不同的球,从布袋里任意摸出1个球,所有可能一共有11种情况,
其中红球有5个,从布袋里任意摸出1个球,红球出现的可能情况只有5种,
从布袋里任意摸出1个球,是红球的概率为.
故选:D.
【点睛】本题考查了简单事件的概率,属于基础题型,熟知概率的计算方法是解题关键.
6.D
【分析】因为小刚以400米/分的速度匀速骑车5分,可求其行驶的路程对照排除错误选项,“在原地休息”对应在图象上表示时间在增加,而距离不变,即这一线段与x轴平行,“回到原出发地”表示终点的纵坐标为0,综合分析选出正确答案.
【详解】解:∵(米)=2(千米),
∴小刚以400米/分的速度匀速骑车5分行驶的路程为2千米,
而选项A与B中纵轴表示速度,且速度为变量,这与事实不符,故排除选项A与B,
又∵“回到原出发地”表示终点的纵坐标为0,
∴排除选项C,
故选:D.
【点睛】本题考查了函数的图象,解题的关键是理解函数图象的意义.
7.D
【分析】由垂径定理,勾股定理求出,延长交圆于,即可求出的最大面积,当绕点旋转一周时,点运动的路线是以为圆心半径是1的圆,即可求出运动的路线长,以为边向上作正方形,与的公共部分的面积扇形的面积+的面积,于是可以得到答案.
【详解】解:如图①,于,
,
,
,
故A不符合题意;
如图①延长交圆于,此时的面积最大,
,,
的面积,
故B不符合题意;
取的中点,连接,,,
,
,
,
当绕点旋转一周时,点运动的路线是以为圆心半径是1的圆,
运动的路线长是,
故C不符合题意;
如图②四边形是正方形,连接,,则过圆心O,作于,
的面积,
,
的面积的面积的面积,
,
扇形的面积,
以为边向上作正方形,与的公共部分的面积扇形的面积的面积,
故D符合题意.
故选:D.
【点睛】本题考查扇形面积的计算,三角形面积的计算,垂径定理,勾股定理,掌握以上知识点是解题的关键.
8.B
【分析】连接.根据切线的性质可得出,根据直径所对圆周角为直角得出,结合题意易证为等边三角形,最后由含30度角的直角三角形的性质结合勾股定理逐项计算判断即可.
【详解】解:如图,连接.
∵与相切于点D,
∴.
∵,
∴,,
∴,即.
∵,
∴为等边三角形,
∴,
∴,故A错误,不符合题意;
∵,,
∴,
∴,故B正确,符合题意;
∵,,
∴.
∵,
∴,
∴.
∵,
∴,故C错误,不符合题意;
∵是的直径,
∴.
∵为等边三角形,
∴,
∴,
∴,
∴,
∴,
∴,故D错误,不符合题意.
故选B.
【点睛】本题考查切线的性质,圆周角定理的推论,等边三角形的判定和性质,含30度角的直角三角形的性质以及勾股定理.连接常用的辅助线是解题关键.
9.B
【分析】此题考查一元一次不等式组的解法以及解集在数轴上的表示,如果带等号用实心表示,如果不带等号用空心表示.
【详解】解:此题考查一元一次不等式组的解法以及解集在数轴上的表示,如果带等号用实心表示,如果不带等号用空心表示;
,当;
当;
当;
当解集不存在;
分别对应下图中的图;
此题中原不等式组可以化为:,所以由图可知,故选B.
【点睛】本题考查不等式解集在数轴上的表示,掌握方法是关键.
10.B
【分析】根据正方形的性质得到,,再利用锐角三角形函数得到,最后根据勾股定理及全等三角形判定与性质即可解答.
【详解】解:过点作于点,设,
∵是的中点,
∴,
∴,
∵在正方形中,
∴,
∵,
∴设,
∴,
∵,
∴,
∴,
∴,
∴,
∴在中,,
∵正方形是由四个全等的直角三角形和一个小正方形组成,
∴,
∴,
∵在和中,
,
∴,
∴,
∵在中,,
∴,
∴,
故选.
【点睛】本题考查了正方形的性质,全等三角形的判定与性质,勾股定理,锐角三角形函数,掌握锐角三角形函数是解题的关键.
11.
【分析】去括号,根据不等式的性质即可求解.
【详解】解
3-3x>2-4x
-3x+4x>2-3
x>-1
故答案为:.
【点睛】此题主要考查解一元一次不等式,解题的关键是熟知不等式的性质.
12.
【分析】根据题意得x只鸡的足数+y只兔的足数=94,再根据等量关系列出方程即可.
【详解】根据题意,得
2x+4y=94.
故答案为:2x+4y=94.
【点睛】本题主要考查了列二元一次方程组,确定等量关系是列方程的关键.
13.11
【分析】根据成绩频数直方图中各组频数进行计算即可.
【详解】解:由直方图知,成绩在80分及以上的人数共有:8+3=11人,
故答案为:11.
【点睛】本题考查了频数分布直方图,从频数分布直方图中得到各组频数是解题关键.
14. 1.7
【分析】设EP=4x,则AP=5x,AE=3x,得到PF=36-4x,CF=36-3x,图1中由CF=15求出x=7,得到CP=17,表示出sin∠2的值,由此求出折射率n2;图2中由水的折射率为,即,求出sin∠3,得到,列得,解得x由此得到答案.
【详解】解:∵∠1=∠EAP,,
∴,
设EP=4x,则AP=5x,AE=3x,
图1中PF=36-4x,CF=36-3x,
∴36-3x=15,
解得x=7,
∴PF=36-4x=8,
∴CP=17,
∴,
∵,
∴,
∴;
图2,∵水的折射率为,即,
∴,
∴,
∴,
∴,
解得x=,
∴,
∴误差为,
故答案为:1.7;.
【点睛】此题考查了正方形的性质,三角函数问题,正确理解题意及掌握相应的物理知识是解题的关键.
15.
【分析】首先连接OD,由折叠的性质,可得CD=CO,BD=BO,∠DBC=∠OBC,则可得△OBD是等边三角形,继而求得OC的长,即可求得△OBC与△BCD的面积,又在扇形OAB中,∠AOB=90°,半径OA=6,即可求得扇形OAB的面积,继而求得阴影部分面积.
【详解】解:如图,连接OD,
根据折叠的性质,CD=CO,BD=BO,∠DBC=∠OBC,
∴OB=OD=BD,
即△OBD是等边三角形,
∴∠DBO=60°,
∴∠CBO=∠DBO=30°,
∵∠AOB=90°,
∴OC=OB tan∠CBO=6,
∴S△BDC=S△OBC=×OB×OC=×6×=6,
S扇形AOB=π×62=9π,
∴整个阴影部分的面积为:S扇形AOB-S△BDC-S△OBC=9π-6-6=9π-12,
故答案为:.
【点睛】本题考查了折叠的性质、扇形面积公式以及直角三角形的性质.此题难度适中,注意数形结合思想的应用,注意辅助线的作法.
16.
【分析】分别求出不等式,得到不等式的解集即可;
【详解】解:解得:
解得:
故不等式的解集为:
故答案为:
【点睛】本题主要考查不等式组解集的求解,掌握不等式组解集的求解方法是解题的关键.
17.(1)甲图书每本价格是50元,乙图书每本价格为20元
(2)该学校图书馆最多可以购买甲和乙图书共38本
【分析】(1)设乙图书每本价格为x元,则甲图书每本价格是2.5x元,由题意:用800元单独购买甲图书比用800元单独购买乙图书要少24本,列出分式方程,解方程即可;
(2)设购买甲种图书a本,则购买乙种图书(2a+8)本,由题意:用于购买甲、乙两种图书的总经费不超过1060元,列出一元一次不等式,解不等式,进而得出结论.
【详解】(1)设乙图书每本价格为x元,则甲图书每本价格是2.5x元,
根据题意得:,
解得:x=20,
经检验:x=20是原方程的根,
则2.5x=50,
答:甲图书每本价格是50元,乙图书每本价格为20元;
(2)设购买甲种图书a本,则购买乙种图书(2a+8)本,
由题意得:50a+20(2a+8)≤1060,
解得:a≤10,
∴2a+8≤28, 则10+28=38,
答:该学校图书馆最多可以购买甲和乙图书共38本.
【点睛】本题考查了分式方程的应用以及一元一次不等式的应用,解题的关键是:(1)找准等量关系,正确列出分式方程;(2)找出数量关系,正确列出一元一次不等式.
18.(1)甲种拉链的进价为1.6元,乙种拉链的进价为2元
(2)有4种购买方案:①甲种拉链5条,乙种拉链14条;②甲种拉链10条,乙种拉链10条;③甲种拉链15条,乙种拉链6条;④甲种拉链20条,乙种拉链2条
(3)不发生变化,理由见解析
【解析】(1)解:设甲种拉链的进价为每条x元,乙种拉链的进价为每条y元,由题意得:,解得:,答:甲种拉链的进价为1.6元,乙种拉链的进价为2元.
(2)解:设购买甲种拉链m条,乙种拉链n条,由题意得:(1.6+0.4)m+2(1+25%)n=45,整理得:n=18﹣m,∵m、n为正整数,∴或或或,即有4种购买方案:①甲种拉链5条,乙种拉链14条;②甲种拉链10条,乙种拉链10条;③甲种拉链15条,乙种拉链6条;④甲种拉链20条,乙种拉链2条.
(3)解:不发生变化,理由如下:∵利润w=0.4m+2×25%×(18﹣m)=9(元),∴不同方案专卖店获利不发生变化.
【点睛】此题考查了二元一次方程组的应用、二元一次方程的应用,读懂题意,找到等量关系,列出二元一次方程组或二元一次方程是解题的关键.
19.
【分析】先计算乘方及绝对值运算,再计算除法运算,最后算算加减运算即可求出值.
【详解】解:原式=﹣1+|2﹣9|+×(﹣)
=﹣1+7﹣
=6﹣
=
【点睛】本题主要考查了有理数的混合运算,熟练掌握有理数的混合运算法则是解题的关键.
20.(1)证明见解析;
(2)证明见解析
【详解】(1)证明:如图,∵AD平分∠BAC,
∴∠1=∠2,
∵,CD∥AB,
∴.
∵,,
∴,
∴,
∴是等腰三角形;
(2)证明:由(1)得
∴,
∵,,,
∴,
∴,
∴.
【点睛】本题考查了等腰三角形的判定与性质、平行线的性质及全等三角形的判定与性质,熟练掌握等腰三角形的判定与性质是解题的关键.
21.(1)
(2)
【分析】(1)由OB=OC得出C的坐标,再利用待定系数法即可得出结论;
(2)先根据BE=EC求出点E的坐标,再求出BE的长度,把P的坐标用含a的式子表示出来,根据EB=EP即可得出答案.
【详解】(1)解:∵OB=OC,
∴C(0,﹣3),
把A,B,C代入中,
得:,
解得:,
∴抛物线的解析式为;
(2)解:如图,连接BC,
∵EB=EC,
∴E是BC的中点,
∴E的坐标为(,),
∴P的横坐标为,
把A,B代入中,
得:,
解得:,
∴抛物线的解析式为,
把x=代入,得y=,
∴P(,),
∴EP==,
解得a=,
∴a的值为.
【点睛】本题主要考查二次函数的图象与性质,解题的关键是要会用待定系数法求抛物线的解析式,牢记勾股定理的公式.
22.(1)见解析
(2)
【分析】(1)连接OD,根据DE是⊙O的切线,可得∠ODE=90°,由AC=BC,可得∠OBD=∠A,进而可得∠A=∠ODB,可得ODAC,即可证明结论;
(2)连接CD,证明∠CDE=∠ABC,由得,设CE=3x,CD=5x,则DE=4x,根据S△OCE=6可求出x的值,可得CD的长,由可得BC的长,即可得⊙O的半径.
【详解】(1)证明:如图1,连接OD,则OD为⊙O的半径,
∵DE是⊙O的切线,
∴∠ODE=90°,
∵OB=OD,
∴∠OBD=∠ODB,
∵AC=BC,
∴∠OBD=∠A,
∴∠A=∠ODB,
∴ODAC,
∴∠DEC=180°-∠ODE=90°,
∴DE⊥AC;
(2)解:连接CD,如图2,
∵BC为直径,
∴∠BDC=∠CDA=90°,
∴∠CDE+∠EDA=90°,
∵DE⊥AC,
∴∠ADE+∠A=90°,
∴∠A=∠CDE,
∵CA=CB,
∴∠A=∠B,
∴∠CDE=∠ABC,
∴,
设CE=3x,CD=5x,则DE==4x,
∵S△OCE=CE DE=6=6,
∴x=1或x=﹣1(不合题意,舍去),
∴x=1,
∴CD=5,
∵,
∴BC=,
∴⊙O的半径为.
【点睛】此题主要考查了圆的切线的性质定理、圆周角定理、锐角三角函数、勾股定理、等腰三角形的判定和性质等知识,熟练掌握锐角三角函数的定义是解题的关键.
23.(1)见解析
(2)
(3)2-或-1
【分析】(1)连接AC.证明AE⊥AC即可解决问题.
(2)证明△ABC是等边三角形,推出∠ACB=60°,AE=AC tan60°=2,根据求解即可.
(3)分两种情形:①如图2中,当点F在上时.②如图3中,当点F在优弧上时,分别求解即可.
【详解】(1)证明:如图1中,连接AC,
∵四边形ABCD是菱形,
∴AC⊥BD,
又∵BDAE,
∴AC⊥AE,
∴AE是⊙O的切线.
(2)解:如图1中,
∵四边形ABCD是菱形,
∴AB=BC,
又∵AC=BC,
∴△ABC是等边三角形,
∴∠ACB=60°,
∵AC=2,
∴AE=AC tan60°=2,
∴
=
=.
(3)解:分两种情形:①如图2中,当点F在上时,
∵∠DAF=15°,
∴∠DCF=30°,
∵∠ACD=60°,
∴∠ACF=∠FCD,
∴点F是弧AD的中点,
∴CF⊥AD,
∴点F到直线AD的距离=CF-CA cos30°=2-.
②如图3中,当点F在优弧上时,
∵∠DAF=15°,
∴∠DCF=30°,
过点C作CG⊥AD于G,过点F作FH⊥CG于H,
可得∠AFH=15°,∠HFC=30°,
∴CH=1,
∴点F到直线AD的距离=CG-CH=AC cos30°-CH=-1.
综上所述,满足条件的点F到直线AD的距离为2-或-1.
【点睛】本题属于圆综合题,考查了切线的判定,菱形的性质,等边三角形的判定和性质,解直角三角形等知识,解题的关键是学会用分类讨论的思想思考问题,属于中考压轴题.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
