人教版数学八年级下册 20.1数据的集中趋势同步练习
文档属性
| 名称 | 人教版数学八年级下册 20.1数据的集中趋势同步练习 |  | |
| 格式 | docx | ||
| 文件大小 | 178.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-05 21:09:34 | ||
图片预览


文档简介
人教版八年级下册第二十章20.1数据的集中趋势
一、单选题
1.某超市试销一批新款衬衫,一周内销售情况如下表所示,那么超市经理最适宜加大进货量的衬衫型号是( )
型号(厘米) 38 39 40 41 42 43
数量(件) 13 21 35 48 26 8
A.48 B.41 C.40 D.35
2.某校调查了20名男生某周参加篮球运动的次数,调查结果如表所示,那么这20名男生该周参加篮球运动次数的平均数是 ( )
次数/次 2 3 4 5
人数/人 2 2 10 6
A.3次 B.3.5次 C.4次 D.4.5次
3.2022年2月,第24届冬季奥林匹克运动会在北京举行.某校八年级(1)班在班会课开展了冬奥会知识小竞赛,10位同学在这个知识竞赛中的成绩统计结果如表所示,则这10位同学的平均成绩是( )
成绩 7 8 9 10
人数 1 4 3 2
A.8 B.8.5 C.8.6 D.9
4.某语文教师调查了本班10名学生平均每天的课外阅读时间,统计结果如下表所示:
课外阅读时间(小时) 0.5 1 1.5 2
人数 2 3 4 1
那么这10名学生平均每天的课外阅读时间的平均数和众数分别是( )
A.1.2和1.5 B.1.2和4 C.1.25和1.5 D.1.25 和4
5.希望中学规定学生的学期体育成绩满分为100,其中体育课外活动占20%,期中考试成绩占30%,期末考试成绩占50%.若小强的三项成绩(百分制)依次是95,90,91.则小强这学期的体育成绩是( )
A.92 B.91.5 C.91 D.90
6.为了解某小区“全民健身”活动的开展情况,随机对居住在该小区的40名居民一周的体育锻炼时间进行了统计,结果如下表:
锻炼时间(时) 3 4 5 6 7
人数(人) 6 13 14 5 2
这40名居民一周体育锻炼时间的众数和中位数是( )
A.14,5 B.14,6 C.5,5 D.5,6
7.小明同学本学期的数学测试成绩如表,如果规定平时成绩、期中成绩、期末成绩按照计算得出总成绩,则本学期小明的数学总成绩为( )
测试类别 平时 期中 期末
得分(分) 84 80 94
A.86分 B.86.4分 C.87分 D.88分
8.2022年北京冬奥会的单板U形技巧资格赛中,谷爱凌滑完后,六名裁判打分如下:94,94,96,96,96,97,则六名裁判所打分数的众数和中位数分别是( )
A.94,96 B.96,95 C.96,96 D.94,95
9.对于一组数据1,1,3,1,4,下列结论错误的是( )
A.平均数是2 B.众数是1 C.中位数是3 D.方差是1.6
10.某同学对一组数据23,31,32,43,32,5◆,52进行统计分析时,发现其中一个两位数的个位数字被污染看不到了,则下列计算结果一定与被污数字无关的是( )
A.平均数 B.中位数 C.方差 D.众数
11.某班3位同学进行投篮比赛,每人投10次,平均每人投中8次,已知第一、三位同学分别投中8次,10次,那么第二位同学投中( )
A.6次 B.7次 C.8次 D.9次
12.甲、乙两台机床生产某款新产品,前6天生产优等品的数量如表:对两台机床生产优等品数量作如下分析,其中说法正确的是( )
第1天 第2天 第3天 第4天 第5天 第6天
甲 9 8 6 7 8 10
乙 8 7 10 7 8 8
A.它们优等品数量的平均数不同 B.它们优等品数量的中位数不同
C.它们优等品数量的众数不同 D.它们优等品数量的方差不同
二、填空题
13.若一组数据8,8,x,9的众数与平均数相等,则这组数据的中位数是 .
14.某次射击训练中,一小组的成绩如下表所示:
环数 6 7 8 9
人数 1 3 2
若该小组的平均成绩为7.7环,则成绩为8环的人数是 .
15.某电力公司需招聘一名电工技师,对应聘者李某从形象、实践操作、理论检测三个方面进行量化考核.李某各项得分如下表:
考查项目 形象 实践操作 理论检测
李技师 85分 90分 80分
该公司规定:形象、实践操作、理论检测得分分别按20%,50%,30%的比例计入总分,则应聘者李某的总分为 分.
16.某工厂甲、乙两个部门各有员工400人,为了了解这两个部门员工的生产技能情况,进行了抽样调查,过程如下,请补充完整.
收集数据从甲、乙两个部门各随机抽取20名员工,进行了生产技能测试,测试成绩(百分制)如表:
甲 78 86 74 81 75 76 87 70 75 90
75 79 81 70 74 80 86 69 83 77
乙 93 73 88 81 72 81 94 83 77 83
80 81 70 81 73 78 82 80 70 40
整理、描述数据按如下分数段整理、描述这两组样本数据:
成绩x人数 部门 40≤x≤49 50≤x≤59 60≤x≤69 70≤x≤79 80≤x≤89 90≤x≤100
甲 0 0 1 11 7 1
乙 1 0 0 7 10 2
(说明:成绩80分及以上为生产技能优秀,70~79分为生产技能良好,60~69分为生产技能合格,60分以下为生产技能不合格)
分析数据两组样本数据的平均数、中位数、众数如表所示:
部门 平均数 中位数 众数 方差
甲 78.3 77.5 m 33.61
乙 78 n 81 117.5
得出结论
(1)上表中m= ,n= ;
(2)甲、乙两个部门员工的生产技能水平比较均衡的是 部门,估计乙部门生产技能优秀的员工人数为 ;
(3)可以推断出 部门员工的生产技能水平较高,理由为 .(至少从两个不同的角度说明推断的合理性)
17.若一组数据6,x,2,3,4的平均数是4,则这组数据的中位数为 .
18.某校组织学生参加植树活动,活动结束后,统计了九年级甲班50名学生每人植树的情况,绘制了如下的统计表:
植树棵数 3 4 5 6
人数 20 15 10 5
那么这50名学生平均每人植树 棵.
三、解答题
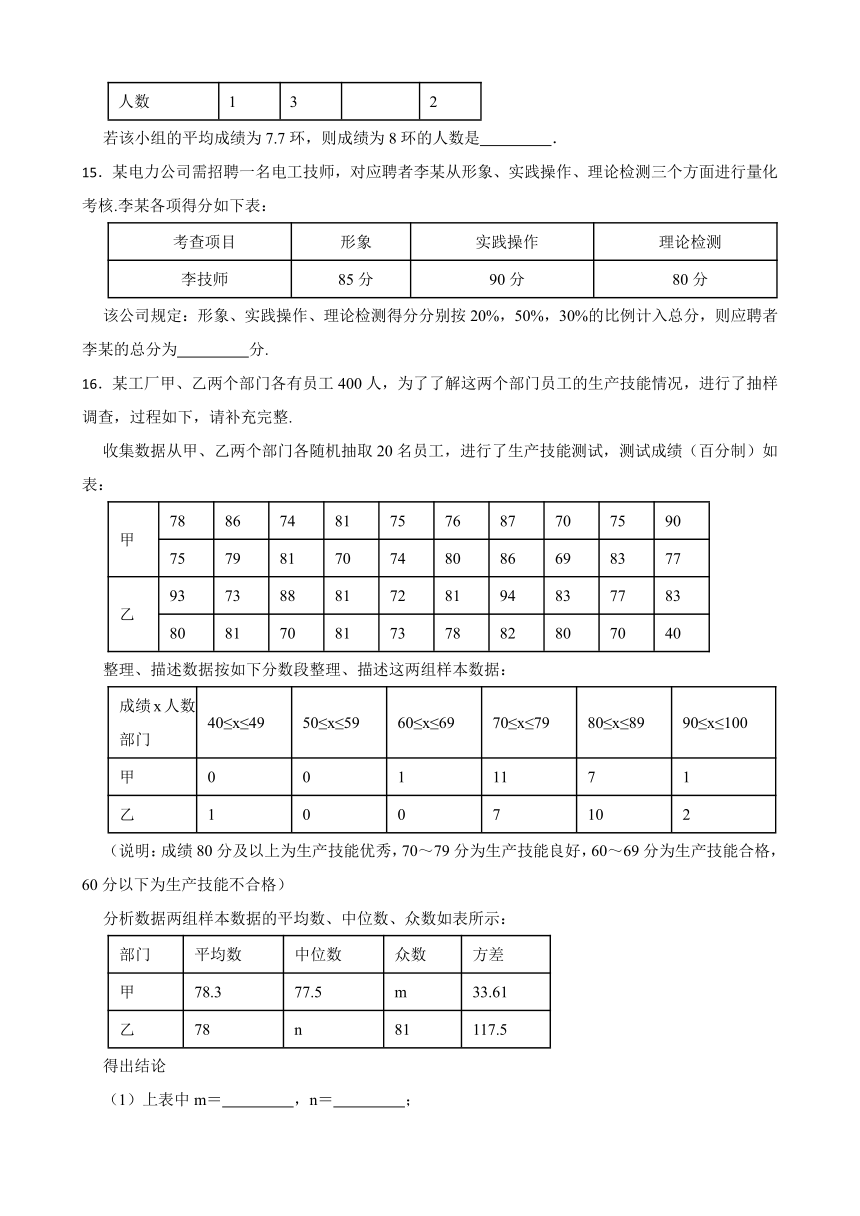
19.农科院为了解某种小麦的长势,从中随机抽取了部分麦苗,对苗高(单位: )进行了测量.根据统计的结果,绘制出如下的统计图①和图②.
请根据相关信息,解答下列问题:
(Ⅰ)本次抽取的麦苗的株数为 ▲ ,图①中m的值为 ▲ ;
(Ⅱ)求统计的这组苗高数据的平均数、众数和中位数.
20.某商场招聘员工一名,现有甲、乙、丙三人竞聘.通过计算机、语言和商品知识三项测试,他们各自成绩(百分制)如下表所示.
应试者 计算机 语言 商品知识
甲
乙
丙
若商场需要招聘负责将商品拆装上架的人员,计算机、语言和商品知识成绩分别占20%,30%,50%,计算三名应试者的平均成绩.从成绩看,应该录取谁?
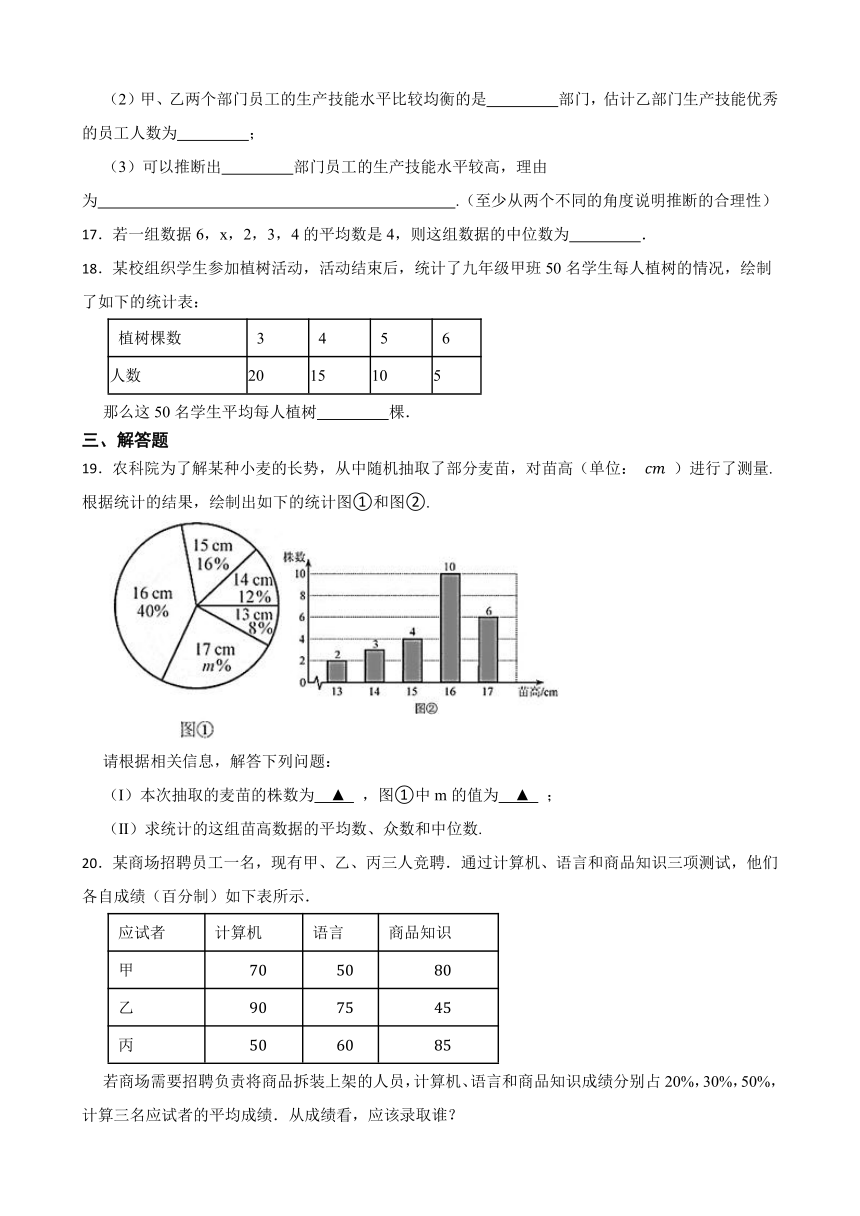
21.随着移动计算技术和无线网络的快速发展,移动学习方式越来越引起人们的关注,某校计划将这种学习方式应用到教育学中,从全校1500名学生中随机抽取了部分学生,对其家庭中拥有的移动设备的情况进行调查,并绘制出如下的统计图①和图②,根据相关信息,解答下列问题:
(1)本次接受随机抽样调查的学生人数为 ,图①中m的值为 ;
(2)求本次调查获取的样本数据的众数、中位数和平均数;
(3)根据样本数据,估计该校1500名学生家庭中拥有3台移动设备的学生人数.
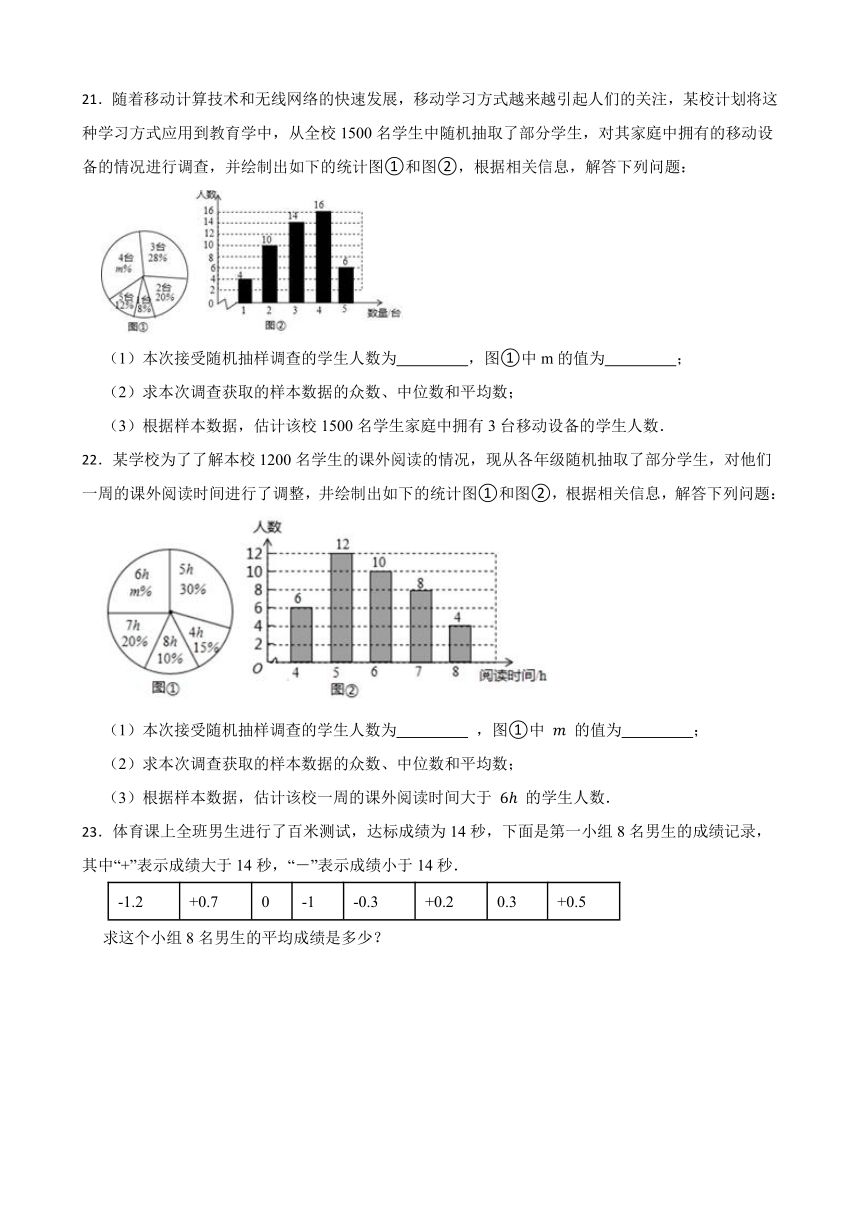
22.某学校为了了解本校1200名学生的课外阅读的情况,现从各年级随机抽取了部分学生,对他们一周的课外阅读时间进行了调整,井绘制出如下的统计图①和图②,根据相关信息,解答下列问题:
(1)本次接受随机抽样调查的学生人数为 ,图①中 的值为 ;
(2)求本次调查获取的样本数据的众数、中位数和平均数;
(3)根据样本数据,估计该校一周的课外阅读时间大于 的学生人数.
23.体育课上全班男生进行了百米测试,达标成绩为14秒,下面是第一小组8名男生的成绩记录,其中“+”表示成绩大于14秒,“-”表示成绩小于14秒.
-1.2 +0.7 0 -1 -0.3 +0.2 0.3 +0.5
求这个小组8名男生的平均成绩是多少?
答案解析部分
1.【答案】B
【解析】【解答】解:由统计表的数据可以看出,型号41的衬衫是卖得最多的,
所以超市经理最适宜加大进货量的衬衫型号为41;
故答案为:B.
【分析】众数是指一组数据中出现次数最多的数,根据众数的定义并结合统计表可判断求解.
2.【答案】C
【解析】【解答】解:=4,
∴20名男生该周参加篮球运动次数的平均数是4次.
故答案为:C.
【分析】根据加权平均数的计算公式列式进行计算,即可得出答案.
3.【答案】C
【解析】【解答】解:这10位同学的平均成绩是=8.6,
故答案为:C.
【分析】利用平均数的计算方法求解即可。
4.【答案】A
【解析】【解答】解:10名学生的每天阅读时间的平均数为 ;
学生平均每天阅读时间出现次数最多的是1.5小时,共出现4次,因此众数是1.5;
故答案为:A.
【分析】根据平均数、众数的计算方法求出结果即可.
5.【答案】B
【解析】【解答】解:根据题意得
即小强这学期的体育成绩是91.5.
故答案为:B.
【分析】利用课外活动成绩×所占的比例+期中考试成绩×所占的比例+期末考试成绩×所占的比例就可求出小强这学期的体育成绩.
6.【答案】C
【解析】【解答】由统计表可知:体育锻炼时间最多的是5小时,故众数是5小时;统计表中是按从小到大的顺序排列的,最中间两个人的锻炼时间都是5小时,故中位数是5小时.
故答案为:C.
【分析】根据中位数、众数的意义,分别求出这组数据的中位数、众数后,再进行选择即可。
7.【答案】B
【解析】【解答】解:总成绩为:
故答案为:B.
【分析】这里总成绩就是求加权平均数,按照其定义即可求得.
8.【答案】C
【解析】【解答】解:排序为94,94,96,96,96,97,
处于最中间的数是96,96,它们的平均数为96,
∴这组数据的中位数是96,
∵96出现了3次,是这组数据中出现次数最多的数,
∴这组数据的众数为96.
故答案为:C
【分析】求中位数的方法是:把数据先按从小到大的顺序排列,位于最中间的一个数(或两个数的平均数)为中位数;众数是一组数据中出现次数最多的数据,分别求出这组数据的众数和中位数..
9.【答案】C
【解析】【解答】解:将这组数据重新排列为1,1,1,3,4,
所以这组数据的平均数为×(1+1+1+3+4)=2,
中位数为1,众数为1,
方差为×[3×(1-2)2+(3-2)2+(4-2)2]=1.6,
故答案为:C.
【分析】利用众数、平均数、方差和中位数的定义及计算方法逐项判断即可。
10.【答案】B
【解析】【解答】解:根据题意,平均数、方差、众数都与数列中的每个数据有关,且将数据从小到大排列时,5◆数是以5开头,大于43(43排在第五位置,总数有7个),5◆数可能排在第六或第七位置,
∴中位数与5◆无关.
故答案为:B.
【分析】利用众数、平均数、方差和中位数的定义及计算方法逐项判断即可。
11.【答案】A
【解析】【解答】解:设第二位同学投中x次,
∵平均每人投中8次,
∴=8,
解得:x=6,
∴第二位同学投中6次,
故答案为:A.
【分析】设第二位同学投中x次,根据平均数为8次,建立方程求解,即可解答.
12.【答案】D
【解析】【解答】甲机床生产优等品数量的平均数为 8,
乙机床生产优等品数量的平均数为 8,
∴它们优等品数量的平均数相同,故A选项说法不符合题意,
甲机床生产优等品数量的中位数为 =8,
乙机床生产优等品数量的中位数为 =8,
∴它们优等品数量的中位数相同,故B选项说法不符合题意,
甲机床生产优等品数量的众数为8,
乙机床生产优等品数量的众数为8,
∴它们优等品数量的众数相同,故C选项说法不符合题意,
甲机床生产优等品数量的方差为 ,
乙机床生产优等品数量的方差为 =1,
∴它们优等品数量的方差不同,故D选项说法符合题意,
故答案为:D.
【分析】根据平均数,中位数,众数和方差的定义,再结合表格中的数据计算求解即可。
13.【答案】8
【解析】【解答】解:这组数据的平均数=(2×8+x+9)÷5,
∵这组数据的众数与平均数相等,
∴(2×8+x+9)÷4=8,
∴x=7,
∴这组数据为7,8,8,9,
∴中位数=(8+8)÷2=8.
故答案为:8.
【分析】先表示出这组数据的平均数,再由这组数据的众数与平均数相等,可得(2×8+x+9)÷4=8,解得x=7,再将这组数据按序排列,根据中位数计算方法即可得出答案.
14.【答案】4
【解析】【解答】设成绩为8环的人数是x人,平均数的计算方法是求出所有数据的和,然后除以数据的总个数,据此列出方程,再求解.
设成绩为8环的人数是x人,
由题意得(6×1+7×3+8x+9×2)÷(1+3+x+2)=7.7,解得x=4,
则成绩为8环的人数是4.
【分析】根据该小组的平均成绩为7.7环,列方程计算求解即可。
15.【答案】86
【解析】【解答】解:85×20%+90×50%+80×30%=86,
∴应聘者李某的总分为86分.
故答案为:86.
【分析】根据加权平均数的公式列式进行计算,即可得出答案.
16.【答案】(1)75;80.5
(2)甲;240
(3)甲;①甲平均分较高;②甲没有技能不合格的员工
【解析】【解答】解:(1)由题中第一个表格可知:
甲中出现次数最多的是75,则众数为75,即m=75;
由第二个表格可知:
乙的第10和11个数据在80≤x≤89范围内;
再观察第一个表可知,第10个数为80,第11个数为81,
故中位数为(80+81)÷2=80.5,
即n=80.5.
故答案为:75,80.5;
(2)∵甲的方差为33.61,乙的方差为117.5,
∴甲的方差<乙的方差,
∴甲、乙两个部门员工的生产技能水平比较均衡的是甲部门;
∵成绩80分及以上为生产技能优秀,乙符合此条件的有10+2=12(人),
∴估计乙部门生产技能优秀的员工人数为:
=240(人).
故答案为:甲,240;
(3)可以推断出甲部门员工的生产技能水平较高,理由为:
①甲平均分较高;②甲没有技能不合格的员工.
故答案为:甲;①甲平均分较高;②甲没有技能不合格的员工.
【分析】(1)将一组数据按从小到大或从大到小排列后,如果这组数据的个数是奇数个,则最中间位置的数就是这组数据的中位数,如果这组数据的个数是偶数个,则最中间两个数据的平均数就是这组数据的中位数;众数是一组数据中出现次数最多的数据;利用表中数据可求出m,n的值;
(2)利用比值数据可知甲和乙的方差,可得到甲的方差<乙的方差,利用方差越大数据的波动越大,可得到甲、乙两个部门员工的生产技能水平比较均衡的部门;成绩80分及以上为生产技能优秀,乙符合此条件的有12人;再利用乙部门的总员工人数×成绩80分及以上的员工人数所占的百分比,列式计算可求出结果.
(3)利用表中的数据,从方差,平均数等方面进行分析比较,可得答案.
17.【答案】4
【解析】【解答】∵数据6,x,2,3,4的平均数是4,
∴,
解得:=5,
这组数据按照从小到大的顺序排列为:2,3,4,5,6,
则中位数为4.
故答案为:4.
【分析】利用平均数的计算方法求出x的值,再利用中位数的定义求解即可。
18.【答案】4
【解析】【解答】解:平均每人种树:(棵),
故答案为:4.
【分析】运用加权平均数的定义运算即可求解.
19.【答案】解:(Ⅰ)由图②可知:
本次抽取的麦苗株数为:2+3+4+10+6=25(株),
其中17cm的麦苗株数为6株,故其所占的比为6÷25=0.24=24%,即m=24.
故答案为:25,24;(Ⅱ)观察条形统计图,
这组麦苗得平均数为: ,
在这组数据中,16出现了10次,出现的次数最多,
这组数据的众数为16.
将这组数据按从小到大的顺序排列,其中处于中间位置的数是16,
这组数据的中位数为16.
故答案为:麦苗高的平均数是15.6,众数是16,中位数是16.
【解析】【分析】(1)由图②中条形统计图即可求出麦苗的株数;用17cm的麦苗株数6除以总株数24即可得到m的值;
(2)利用加权平均数的计算方法即可算出该组数据的平均数;这组数据中出现次数最多的数据就是这组数据的众数;将这24个数据按从小到大排列后,排最中间位置的两个数的平均数就是这组数据的中位数,据此即可得出答案.
20.【答案】解:甲最终的成绩是70×20%+50×30%+80×50%=69(分),
乙最终的成绩是90×20%+75×30%+45×50%=63(分),
丙最终的成绩是50×20%+60×30%+85×50%=70.5(分),
故从成绩看,应该录取丙.
【解析】【分析】根据加权平均数的公式列式计算可得。
21.【答案】解:(Ⅰ)50|32;(Ⅱ)∵这组样本数据中,4出现了16次,出现次数最多, ∴这组数据的众数为4; ∵将这组数据从小到大排列,其中处于中间的两个数均为3,有 =3, ∴这组数据的中位数是3; 由条形统计图可得 =3.2, ∴这组数据的平均数是3.2. (Ⅲ)1500×28%=420(人). 答:估计该校学生家庭中;拥有3台移动设备的学生人数约为420人。
(1)50;32
(2)∵这组样本数据中,4出现了16次,出现次数最多,
∴这组数据的众数为4;
∵将这组数据从小到大排列,其中处于中间的两个数均为3,有 =3,
∴这组数据的中位数是3;
由条形统计图可得 =3.2,
∴这组数据的平均数是3.2.
(3)解:1500×28%=420(人).
答:估计该校学生家庭中;拥有3台移动设备的学生人数约为420人。
【解析】【解答】解:(1)本次接受随机抽样调查的学生人数为: =50(人),
∵ ×100=32%,
∴图①中m的值为32.
故答案为50、32;
【分析】(1)根据家庭中拥有1台移动设备的人数及所占的百分比可求出总人数,将拥有4台移动设备的人数除以总人数即可得m的值;
(2)根据众数、中位数、加权平均数的定义计算即可;
(3)将样本中拥有3台移动设备的学生人数所占的比例乘以1500即可。
22.【答案】(1)40;25
(2)∵这组样本数据中,5出现了12次,出现次数最多,
∴这组数据的众数为5;
∵将这组数据从小到大排列,其中处于中间的两个数均为6,则 ,
∴这组数据的中位数是6;
由条形统计图可得 ,
∴这组数据的平均数是5.8;
(3) (人)
答:估计该校一周的课外阅读时间大于 的学生人数约为360人.
【解析】【解答】解:(1)6+12+10+8+4=40; ,∴m=25;
【分析】(1)根据扇形统计图和条形统计图中的数据计算求解即可;
(2)根据众数、中位数和平均数的定义计算求解即可;
(3)根据某学校为了了解本校1200名学生的课外阅读的情况,列式计算求解即可。
23.【答案】解: (秒)
(秒).
答:这个小组8名男生的平均成绩是13.9秒.
【解析】【分析】先求出表格中记录数据的平均数,再加上达标成绩14秒即可.
一、单选题
1.某超市试销一批新款衬衫,一周内销售情况如下表所示,那么超市经理最适宜加大进货量的衬衫型号是( )
型号(厘米) 38 39 40 41 42 43
数量(件) 13 21 35 48 26 8
A.48 B.41 C.40 D.35
2.某校调查了20名男生某周参加篮球运动的次数,调查结果如表所示,那么这20名男生该周参加篮球运动次数的平均数是 ( )
次数/次 2 3 4 5
人数/人 2 2 10 6
A.3次 B.3.5次 C.4次 D.4.5次
3.2022年2月,第24届冬季奥林匹克运动会在北京举行.某校八年级(1)班在班会课开展了冬奥会知识小竞赛,10位同学在这个知识竞赛中的成绩统计结果如表所示,则这10位同学的平均成绩是( )
成绩 7 8 9 10
人数 1 4 3 2
A.8 B.8.5 C.8.6 D.9
4.某语文教师调查了本班10名学生平均每天的课外阅读时间,统计结果如下表所示:
课外阅读时间(小时) 0.5 1 1.5 2
人数 2 3 4 1
那么这10名学生平均每天的课外阅读时间的平均数和众数分别是( )
A.1.2和1.5 B.1.2和4 C.1.25和1.5 D.1.25 和4
5.希望中学规定学生的学期体育成绩满分为100,其中体育课外活动占20%,期中考试成绩占30%,期末考试成绩占50%.若小强的三项成绩(百分制)依次是95,90,91.则小强这学期的体育成绩是( )
A.92 B.91.5 C.91 D.90
6.为了解某小区“全民健身”活动的开展情况,随机对居住在该小区的40名居民一周的体育锻炼时间进行了统计,结果如下表:
锻炼时间(时) 3 4 5 6 7
人数(人) 6 13 14 5 2
这40名居民一周体育锻炼时间的众数和中位数是( )
A.14,5 B.14,6 C.5,5 D.5,6
7.小明同学本学期的数学测试成绩如表,如果规定平时成绩、期中成绩、期末成绩按照计算得出总成绩,则本学期小明的数学总成绩为( )
测试类别 平时 期中 期末
得分(分) 84 80 94
A.86分 B.86.4分 C.87分 D.88分
8.2022年北京冬奥会的单板U形技巧资格赛中,谷爱凌滑完后,六名裁判打分如下:94,94,96,96,96,97,则六名裁判所打分数的众数和中位数分别是( )
A.94,96 B.96,95 C.96,96 D.94,95
9.对于一组数据1,1,3,1,4,下列结论错误的是( )
A.平均数是2 B.众数是1 C.中位数是3 D.方差是1.6
10.某同学对一组数据23,31,32,43,32,5◆,52进行统计分析时,发现其中一个两位数的个位数字被污染看不到了,则下列计算结果一定与被污数字无关的是( )
A.平均数 B.中位数 C.方差 D.众数
11.某班3位同学进行投篮比赛,每人投10次,平均每人投中8次,已知第一、三位同学分别投中8次,10次,那么第二位同学投中( )
A.6次 B.7次 C.8次 D.9次
12.甲、乙两台机床生产某款新产品,前6天生产优等品的数量如表:对两台机床生产优等品数量作如下分析,其中说法正确的是( )
第1天 第2天 第3天 第4天 第5天 第6天
甲 9 8 6 7 8 10
乙 8 7 10 7 8 8
A.它们优等品数量的平均数不同 B.它们优等品数量的中位数不同
C.它们优等品数量的众数不同 D.它们优等品数量的方差不同
二、填空题
13.若一组数据8,8,x,9的众数与平均数相等,则这组数据的中位数是 .
14.某次射击训练中,一小组的成绩如下表所示:
环数 6 7 8 9
人数 1 3 2
若该小组的平均成绩为7.7环,则成绩为8环的人数是 .
15.某电力公司需招聘一名电工技师,对应聘者李某从形象、实践操作、理论检测三个方面进行量化考核.李某各项得分如下表:
考查项目 形象 实践操作 理论检测
李技师 85分 90分 80分
该公司规定:形象、实践操作、理论检测得分分别按20%,50%,30%的比例计入总分,则应聘者李某的总分为 分.
16.某工厂甲、乙两个部门各有员工400人,为了了解这两个部门员工的生产技能情况,进行了抽样调查,过程如下,请补充完整.
收集数据从甲、乙两个部门各随机抽取20名员工,进行了生产技能测试,测试成绩(百分制)如表:
甲 78 86 74 81 75 76 87 70 75 90
75 79 81 70 74 80 86 69 83 77
乙 93 73 88 81 72 81 94 83 77 83
80 81 70 81 73 78 82 80 70 40
整理、描述数据按如下分数段整理、描述这两组样本数据:
成绩x人数 部门 40≤x≤49 50≤x≤59 60≤x≤69 70≤x≤79 80≤x≤89 90≤x≤100
甲 0 0 1 11 7 1
乙 1 0 0 7 10 2
(说明:成绩80分及以上为生产技能优秀,70~79分为生产技能良好,60~69分为生产技能合格,60分以下为生产技能不合格)
分析数据两组样本数据的平均数、中位数、众数如表所示:
部门 平均数 中位数 众数 方差
甲 78.3 77.5 m 33.61
乙 78 n 81 117.5
得出结论
(1)上表中m= ,n= ;
(2)甲、乙两个部门员工的生产技能水平比较均衡的是 部门,估计乙部门生产技能优秀的员工人数为 ;
(3)可以推断出 部门员工的生产技能水平较高,理由为 .(至少从两个不同的角度说明推断的合理性)
17.若一组数据6,x,2,3,4的平均数是4,则这组数据的中位数为 .
18.某校组织学生参加植树活动,活动结束后,统计了九年级甲班50名学生每人植树的情况,绘制了如下的统计表:
植树棵数 3 4 5 6
人数 20 15 10 5
那么这50名学生平均每人植树 棵.
三、解答题
19.农科院为了解某种小麦的长势,从中随机抽取了部分麦苗,对苗高(单位: )进行了测量.根据统计的结果,绘制出如下的统计图①和图②.
请根据相关信息,解答下列问题:
(Ⅰ)本次抽取的麦苗的株数为 ▲ ,图①中m的值为 ▲ ;
(Ⅱ)求统计的这组苗高数据的平均数、众数和中位数.
20.某商场招聘员工一名,现有甲、乙、丙三人竞聘.通过计算机、语言和商品知识三项测试,他们各自成绩(百分制)如下表所示.
应试者 计算机 语言 商品知识
甲
乙
丙
若商场需要招聘负责将商品拆装上架的人员,计算机、语言和商品知识成绩分别占20%,30%,50%,计算三名应试者的平均成绩.从成绩看,应该录取谁?
21.随着移动计算技术和无线网络的快速发展,移动学习方式越来越引起人们的关注,某校计划将这种学习方式应用到教育学中,从全校1500名学生中随机抽取了部分学生,对其家庭中拥有的移动设备的情况进行调查,并绘制出如下的统计图①和图②,根据相关信息,解答下列问题:
(1)本次接受随机抽样调查的学生人数为 ,图①中m的值为 ;
(2)求本次调查获取的样本数据的众数、中位数和平均数;
(3)根据样本数据,估计该校1500名学生家庭中拥有3台移动设备的学生人数.
22.某学校为了了解本校1200名学生的课外阅读的情况,现从各年级随机抽取了部分学生,对他们一周的课外阅读时间进行了调整,井绘制出如下的统计图①和图②,根据相关信息,解答下列问题:
(1)本次接受随机抽样调查的学生人数为 ,图①中 的值为 ;
(2)求本次调查获取的样本数据的众数、中位数和平均数;
(3)根据样本数据,估计该校一周的课外阅读时间大于 的学生人数.
23.体育课上全班男生进行了百米测试,达标成绩为14秒,下面是第一小组8名男生的成绩记录,其中“+”表示成绩大于14秒,“-”表示成绩小于14秒.
-1.2 +0.7 0 -1 -0.3 +0.2 0.3 +0.5
求这个小组8名男生的平均成绩是多少?
答案解析部分
1.【答案】B
【解析】【解答】解:由统计表的数据可以看出,型号41的衬衫是卖得最多的,
所以超市经理最适宜加大进货量的衬衫型号为41;
故答案为:B.
【分析】众数是指一组数据中出现次数最多的数,根据众数的定义并结合统计表可判断求解.
2.【答案】C
【解析】【解答】解:=4,
∴20名男生该周参加篮球运动次数的平均数是4次.
故答案为:C.
【分析】根据加权平均数的计算公式列式进行计算,即可得出答案.
3.【答案】C
【解析】【解答】解:这10位同学的平均成绩是=8.6,
故答案为:C.
【分析】利用平均数的计算方法求解即可。
4.【答案】A
【解析】【解答】解:10名学生的每天阅读时间的平均数为 ;
学生平均每天阅读时间出现次数最多的是1.5小时,共出现4次,因此众数是1.5;
故答案为:A.
【分析】根据平均数、众数的计算方法求出结果即可.
5.【答案】B
【解析】【解答】解:根据题意得
即小强这学期的体育成绩是91.5.
故答案为:B.
【分析】利用课外活动成绩×所占的比例+期中考试成绩×所占的比例+期末考试成绩×所占的比例就可求出小强这学期的体育成绩.
6.【答案】C
【解析】【解答】由统计表可知:体育锻炼时间最多的是5小时,故众数是5小时;统计表中是按从小到大的顺序排列的,最中间两个人的锻炼时间都是5小时,故中位数是5小时.
故答案为:C.
【分析】根据中位数、众数的意义,分别求出这组数据的中位数、众数后,再进行选择即可。
7.【答案】B
【解析】【解答】解:总成绩为:
故答案为:B.
【分析】这里总成绩就是求加权平均数,按照其定义即可求得.
8.【答案】C
【解析】【解答】解:排序为94,94,96,96,96,97,
处于最中间的数是96,96,它们的平均数为96,
∴这组数据的中位数是96,
∵96出现了3次,是这组数据中出现次数最多的数,
∴这组数据的众数为96.
故答案为:C
【分析】求中位数的方法是:把数据先按从小到大的顺序排列,位于最中间的一个数(或两个数的平均数)为中位数;众数是一组数据中出现次数最多的数据,分别求出这组数据的众数和中位数..
9.【答案】C
【解析】【解答】解:将这组数据重新排列为1,1,1,3,4,
所以这组数据的平均数为×(1+1+1+3+4)=2,
中位数为1,众数为1,
方差为×[3×(1-2)2+(3-2)2+(4-2)2]=1.6,
故答案为:C.
【分析】利用众数、平均数、方差和中位数的定义及计算方法逐项判断即可。
10.【答案】B
【解析】【解答】解:根据题意,平均数、方差、众数都与数列中的每个数据有关,且将数据从小到大排列时,5◆数是以5开头,大于43(43排在第五位置,总数有7个),5◆数可能排在第六或第七位置,
∴中位数与5◆无关.
故答案为:B.
【分析】利用众数、平均数、方差和中位数的定义及计算方法逐项判断即可。
11.【答案】A
【解析】【解答】解:设第二位同学投中x次,
∵平均每人投中8次,
∴=8,
解得:x=6,
∴第二位同学投中6次,
故答案为:A.
【分析】设第二位同学投中x次,根据平均数为8次,建立方程求解,即可解答.
12.【答案】D
【解析】【解答】甲机床生产优等品数量的平均数为 8,
乙机床生产优等品数量的平均数为 8,
∴它们优等品数量的平均数相同,故A选项说法不符合题意,
甲机床生产优等品数量的中位数为 =8,
乙机床生产优等品数量的中位数为 =8,
∴它们优等品数量的中位数相同,故B选项说法不符合题意,
甲机床生产优等品数量的众数为8,
乙机床生产优等品数量的众数为8,
∴它们优等品数量的众数相同,故C选项说法不符合题意,
甲机床生产优等品数量的方差为 ,
乙机床生产优等品数量的方差为 =1,
∴它们优等品数量的方差不同,故D选项说法符合题意,
故答案为:D.
【分析】根据平均数,中位数,众数和方差的定义,再结合表格中的数据计算求解即可。
13.【答案】8
【解析】【解答】解:这组数据的平均数=(2×8+x+9)÷5,
∵这组数据的众数与平均数相等,
∴(2×8+x+9)÷4=8,
∴x=7,
∴这组数据为7,8,8,9,
∴中位数=(8+8)÷2=8.
故答案为:8.
【分析】先表示出这组数据的平均数,再由这组数据的众数与平均数相等,可得(2×8+x+9)÷4=8,解得x=7,再将这组数据按序排列,根据中位数计算方法即可得出答案.
14.【答案】4
【解析】【解答】设成绩为8环的人数是x人,平均数的计算方法是求出所有数据的和,然后除以数据的总个数,据此列出方程,再求解.
设成绩为8环的人数是x人,
由题意得(6×1+7×3+8x+9×2)÷(1+3+x+2)=7.7,解得x=4,
则成绩为8环的人数是4.
【分析】根据该小组的平均成绩为7.7环,列方程计算求解即可。
15.【答案】86
【解析】【解答】解:85×20%+90×50%+80×30%=86,
∴应聘者李某的总分为86分.
故答案为:86.
【分析】根据加权平均数的公式列式进行计算,即可得出答案.
16.【答案】(1)75;80.5
(2)甲;240
(3)甲;①甲平均分较高;②甲没有技能不合格的员工
【解析】【解答】解:(1)由题中第一个表格可知:
甲中出现次数最多的是75,则众数为75,即m=75;
由第二个表格可知:
乙的第10和11个数据在80≤x≤89范围内;
再观察第一个表可知,第10个数为80,第11个数为81,
故中位数为(80+81)÷2=80.5,
即n=80.5.
故答案为:75,80.5;
(2)∵甲的方差为33.61,乙的方差为117.5,
∴甲的方差<乙的方差,
∴甲、乙两个部门员工的生产技能水平比较均衡的是甲部门;
∵成绩80分及以上为生产技能优秀,乙符合此条件的有10+2=12(人),
∴估计乙部门生产技能优秀的员工人数为:
=240(人).
故答案为:甲,240;
(3)可以推断出甲部门员工的生产技能水平较高,理由为:
①甲平均分较高;②甲没有技能不合格的员工.
故答案为:甲;①甲平均分较高;②甲没有技能不合格的员工.
【分析】(1)将一组数据按从小到大或从大到小排列后,如果这组数据的个数是奇数个,则最中间位置的数就是这组数据的中位数,如果这组数据的个数是偶数个,则最中间两个数据的平均数就是这组数据的中位数;众数是一组数据中出现次数最多的数据;利用表中数据可求出m,n的值;
(2)利用比值数据可知甲和乙的方差,可得到甲的方差<乙的方差,利用方差越大数据的波动越大,可得到甲、乙两个部门员工的生产技能水平比较均衡的部门;成绩80分及以上为生产技能优秀,乙符合此条件的有12人;再利用乙部门的总员工人数×成绩80分及以上的员工人数所占的百分比,列式计算可求出结果.
(3)利用表中的数据,从方差,平均数等方面进行分析比较,可得答案.
17.【答案】4
【解析】【解答】∵数据6,x,2,3,4的平均数是4,
∴,
解得:=5,
这组数据按照从小到大的顺序排列为:2,3,4,5,6,
则中位数为4.
故答案为:4.
【分析】利用平均数的计算方法求出x的值,再利用中位数的定义求解即可。
18.【答案】4
【解析】【解答】解:平均每人种树:(棵),
故答案为:4.
【分析】运用加权平均数的定义运算即可求解.
19.【答案】解:(Ⅰ)由图②可知:
本次抽取的麦苗株数为:2+3+4+10+6=25(株),
其中17cm的麦苗株数为6株,故其所占的比为6÷25=0.24=24%,即m=24.
故答案为:25,24;(Ⅱ)观察条形统计图,
这组麦苗得平均数为: ,
在这组数据中,16出现了10次,出现的次数最多,
这组数据的众数为16.
将这组数据按从小到大的顺序排列,其中处于中间位置的数是16,
这组数据的中位数为16.
故答案为:麦苗高的平均数是15.6,众数是16,中位数是16.
【解析】【分析】(1)由图②中条形统计图即可求出麦苗的株数;用17cm的麦苗株数6除以总株数24即可得到m的值;
(2)利用加权平均数的计算方法即可算出该组数据的平均数;这组数据中出现次数最多的数据就是这组数据的众数;将这24个数据按从小到大排列后,排最中间位置的两个数的平均数就是这组数据的中位数,据此即可得出答案.
20.【答案】解:甲最终的成绩是70×20%+50×30%+80×50%=69(分),
乙最终的成绩是90×20%+75×30%+45×50%=63(分),
丙最终的成绩是50×20%+60×30%+85×50%=70.5(分),
故从成绩看,应该录取丙.
【解析】【分析】根据加权平均数的公式列式计算可得。
21.【答案】解:(Ⅰ)50|32;(Ⅱ)∵这组样本数据中,4出现了16次,出现次数最多, ∴这组数据的众数为4; ∵将这组数据从小到大排列,其中处于中间的两个数均为3,有 =3, ∴这组数据的中位数是3; 由条形统计图可得 =3.2, ∴这组数据的平均数是3.2. (Ⅲ)1500×28%=420(人). 答:估计该校学生家庭中;拥有3台移动设备的学生人数约为420人。
(1)50;32
(2)∵这组样本数据中,4出现了16次,出现次数最多,
∴这组数据的众数为4;
∵将这组数据从小到大排列,其中处于中间的两个数均为3,有 =3,
∴这组数据的中位数是3;
由条形统计图可得 =3.2,
∴这组数据的平均数是3.2.
(3)解:1500×28%=420(人).
答:估计该校学生家庭中;拥有3台移动设备的学生人数约为420人。
【解析】【解答】解:(1)本次接受随机抽样调查的学生人数为: =50(人),
∵ ×100=32%,
∴图①中m的值为32.
故答案为50、32;
【分析】(1)根据家庭中拥有1台移动设备的人数及所占的百分比可求出总人数,将拥有4台移动设备的人数除以总人数即可得m的值;
(2)根据众数、中位数、加权平均数的定义计算即可;
(3)将样本中拥有3台移动设备的学生人数所占的比例乘以1500即可。
22.【答案】(1)40;25
(2)∵这组样本数据中,5出现了12次,出现次数最多,
∴这组数据的众数为5;
∵将这组数据从小到大排列,其中处于中间的两个数均为6,则 ,
∴这组数据的中位数是6;
由条形统计图可得 ,
∴这组数据的平均数是5.8;
(3) (人)
答:估计该校一周的课外阅读时间大于 的学生人数约为360人.
【解析】【解答】解:(1)6+12+10+8+4=40; ,∴m=25;
【分析】(1)根据扇形统计图和条形统计图中的数据计算求解即可;
(2)根据众数、中位数和平均数的定义计算求解即可;
(3)根据某学校为了了解本校1200名学生的课外阅读的情况,列式计算求解即可。
23.【答案】解: (秒)
(秒).
答:这个小组8名男生的平均成绩是13.9秒.
【解析】【分析】先求出表格中记录数据的平均数,再加上达标成绩14秒即可.
