《18.2三角形全等的判定》同步练习题(含答案)人教版(五四制)七年级数学下册
文档属性
| 名称 | 《18.2三角形全等的判定》同步练习题(含答案)人教版(五四制)七年级数学下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 368.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-05 00:00:00 | ||
图片预览



文档简介
人教版(五四学制)七年级数学下册《18.2三角形全等的判定》
同步练习题(附答案)
一.选择题
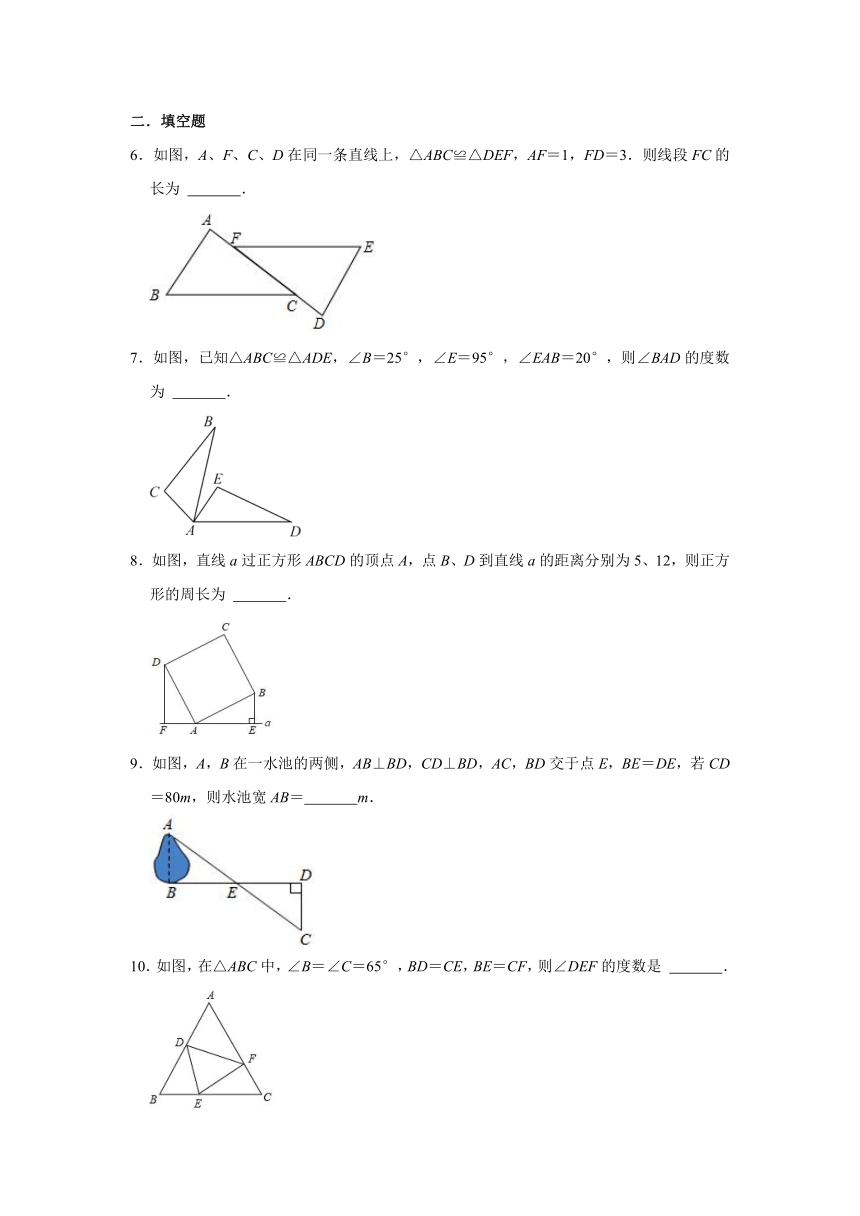
1.如图△ABC≌△CDE,∠B=90°,点C为线段BD上一点,则∠ACE的度数为( )
A.94° B.92° C.90° D.88°
2.如图,△ABC≌△DEF,BC=5,EC=3,则CF的长为( )
A.1 B.2 C.3 D.5
3.如图,△ABC≌△A'B'C',其中∠A=37°,∠C'=23°,则∠B=( )
A.60° B.100° C.120° D.135°
4.如图,已知DB⊥AN于点B,交AE于点O,OC⊥AM于点C,且OB=OC.若∠ADB=54°,则∠OAB的大小为( )
A.15° B.18° C.22° D.30°
5.如图点F在BC,△ABC≌△AEF,AB=AE,∠B=∠E,对于以下结论不正确的是( )
A.AC=AF B.∠FAB=∠B C.EF=BC D.∠AFC=∠ACF
二.填空题
6.如图,A、F、C、D在同一条直线上,△ABC≌△DEF,AF=1,FD=3.则线段FC的长为 .
7.如图,已知△ABC≌△ADE,∠B=25°,∠E=95°,∠EAB=20°,则∠BAD的度数为 .
8.如图,直线a过正方形ABCD的顶点A,点B、D到直线a的距离分别为5、12,则正方形的周长为 .
9.如图,A,B在一水池的两侧,AB⊥BD,CD⊥BD,AC,BD交于点E,BE=DE,若CD=80m,则水池宽AB= m.
10.如图,在△ABC中,∠B=∠C=65°,BD=CE,BE=CF,则∠DEF的度数是 .
11.如图,直线l上有三个正方形A、B、C,若正方形A、C的边长分别为5和7,则正方形B的面积为 .
12.如图,由于受第18号台风“圆规”的影响,学校的某玻璃三角板摔成三块,派小明同学到玻璃店再配一块同样大小的三角板,让小明最省事的方法是带 块去.
13.如图,把两根钢条的中点连在一起,可以做到一个测量工件内槽宽的工具(长钳),在图中要测量工件内槽宽AB,只要测量A′B′长度,其依据是全等三角形判定“ ”和全等三角形对应边相等.
14.如图,公园里有一座假山,要测量假山两端A、B的距离,先在平地上取一个可以直接到达A、B的点C,分别延长AC、BC,到D、E,使CE=CB,CA=CD,连接DE,这样就可以利用三角形全等,通过测量DE的长得到假山两端A、B的距离,则这两个三角形全等的依据是 .
三.解答题
15.如图,△AOB≌△ADC,∠O=90°.已知∠ABC=∠ACB,且BC∥OA,若∠OAD=80°,求∠ABO的度数.
16.如图,点A,B,C在同一直线上,点E在BD上,且△ABD≌△EBC.
(1)若AB=2,BC=3,求DE的长;
(2)判断AD与CE所在直线的位置关系,并说明理由.
17.如图,点A、F、C、D在一条直线上,且BC=EF,BC∥EF,AF=CD.求证:△ABC≌△DEF.
18.在横线上添加一个条件,并完成证明过程:
如图,已知∠AOC=∠BOC, ,求证:△AOC≌△BOC.
19.填补下列证明过程.
如图,△ABC中,D是边BC的中点,延长AD到点E,且CE∥AB.
求证:△ABD≌△ECD.
证明:
∵CE∥AB(已知)
∴∠B=∠DCE ( ).
∵D是边BC的中点(已知)
∴ .
∵AB、BC相交
∴∠ADB=∠EDC ( ).
在△ABD和△ECD中
∴△ABD≌△ECD ( ).
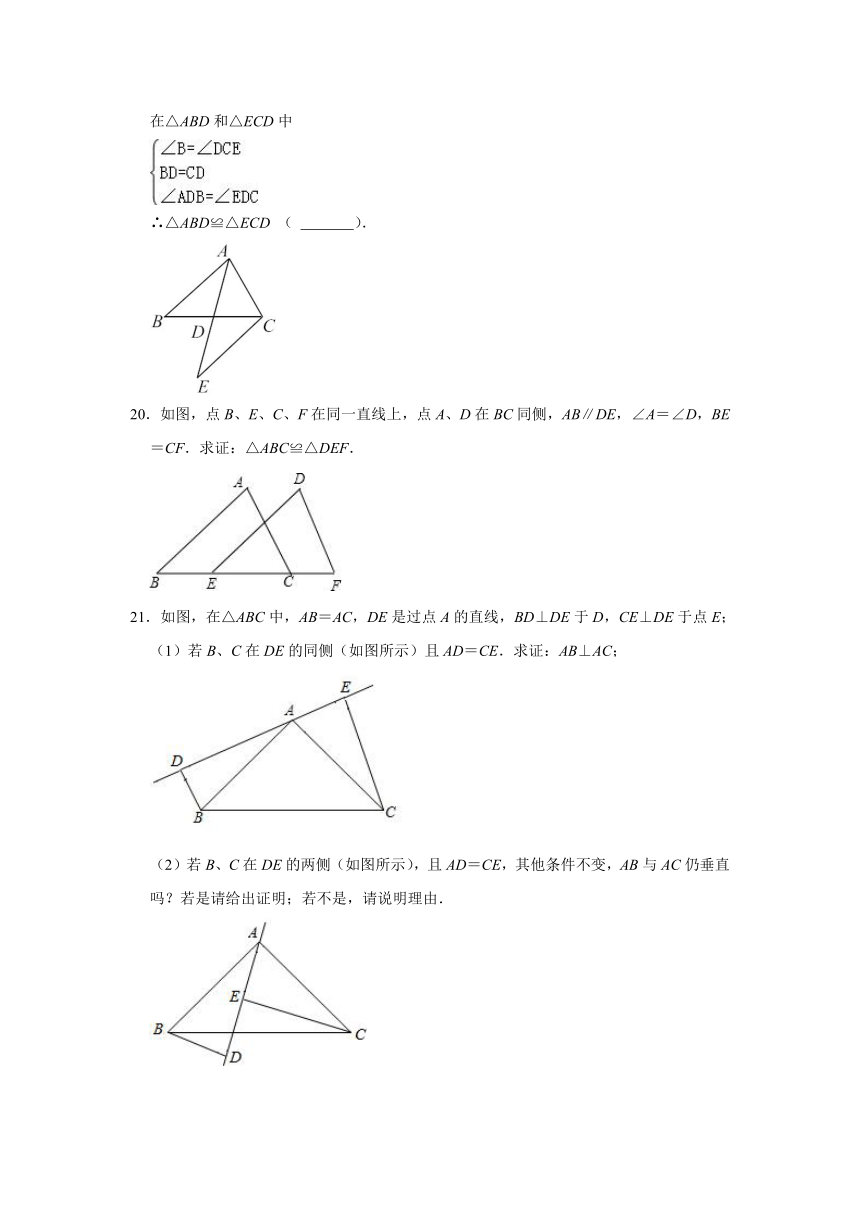
20.如图,点B、E、C、F在同一直线上,点A、D在BC同侧,AB∥DE,∠A=∠D,BE=CF.求证:△ABC≌△DEF.
21.如图,在△ABC中,AB=AC,DE是过点A的直线,BD⊥DE于D,CE⊥DE于点E;
(1)若B、C在DE的同侧(如图所示)且AD=CE.求证:AB⊥AC;
(2)若B、C在DE的两侧(如图所示),且AD=CE,其他条件不变,AB与AC仍垂直吗?若是请给出证明;若不是,请说明理由.
22.已知:如图,∠A=∠D=90°,AC=BD.求证:OB=OC.
23.如图,已知点A,B,C,D在同一条直线上,EA⊥AB,FD⊥AD,AB=CD,若用“HL”证明Rt△AEC≌△Rt△DFB,需添加什么条件?并写出你的证明过程.
24.如图(1),AB⊥AD,ED⊥AD,AB=CD,AC=DE,试说明BC⊥CE的理由;
如图(2),若△ABC向右平移,使得点C移到点D,AB⊥AD,ED⊥AD,AB=CD,AD=DE,探索BD⊥CE的结论是否成立,并说明理由.
25.如图,在△ABC中,D为AB上一点,E为AC的中点,连接DE并延长至点F,连接CF,已知CF∥AB.
(1)求证:E为DF的中点;
(2)若∠ABC=70°,连接BE,BE平分∠ABC,AC平分∠BCF,求∠A的度数.
参考答案
一.选择题
1.解:∵△ABC≌△CDE,
∴∠ACB=∠CED,∠B=∠D=90°,
∵∠CED+∠ECD=90°,
∴∠ACB+∠ECD=90°,
∵∠ACB+∠ECD+∠ACE=180°,
∴∠ACE=90°.
故选:C.
2.解:∵△ABC≌△DEF,
∴EF=BC=5,
∵EC=3,
∴CF=2,
故选:B.
3.解:∵△ABC≌△A'B'C',∠C'=23°,
∴∠C=∠C′=23°,
∵∠A=37°,
∴∠B=180°﹣∠A﹣∠C=180°﹣37°﹣23°=120°,
故选:C.
4.解:∵DB⊥AN,OC⊥AM,
∴∠DBA=∠OCA=90°,
∵OB=OC,OA=OA,
∴△OAB≌△OAC(HL),
∴∠OAB=∠OAC,
∵∠ADB=54°,∠DBA=90°,
∴∠DAB=90°﹣54°=36°,
∴∠OAB=18°.
故选:B.
5.解:∵△ABC≌△AEF,
∴AC=AF,EF=BC,故选项A,C不符合题意,
∴∠AFC=∠ACF,故选项D不符合题意,
故选:B.
二.填空题
6.解:∵△ABC≌△DEF,FD=3,
∴AC=FD=3,
∵AF=1,
∴FC=AC﹣AF=3﹣1=2,
故答案为:2.
7.解:∵△ABC≌△ADE,∠B=25°,
∴∠D=∠B=25°,
∵∠E=95°,
∴∠EAD=180°﹣∠D﹣∠E=60°,
∵∠EAB=20°,
∴∠BAD=∠BAE+∠EAD=20°+60°=80°,
故答案为:80°.
8.解:∵四边形ABCD是正方形,
∴AD=AB=BC=CD,∠BAD=90°,
∵点B、D到直线a的距离分别为5、12,
∴DF⊥AF,BE⊥AE,BE=5,DF=12,
∴∠AFD=∠BEA=90°,∠ADF+∠DAF=90°,
∵∠DAF+∠BAE=90°,
∴∠ADF=∠BAE,
在Rt△AFD和Rt△BEA中,
,
∴Rt△AFD≌Rt△BEA(AAS),
∴DF=AE=12,AF=BE=5,
在Rt△BEA中,由勾股定理得:AB===13,
∴正方形ABCD的周长=4AB=52,
故答案为:52.
9.解:在△ABE和△CDE中,
,
∴△ABE≌△CDE(ASA),
∴CD=AB=80m.
故答案为:80.
10.解:在△DBE和△ECF中,
,
∴△DBE≌△ECF(SAS),
∴∠BDE=∠FEC,
∵∠DEF+∠FEC=∠B+∠BDE,
∴∠DEF=∠B=65°,
故答案为:65°.
11.解:如图,
∵正方形A,C的边长分别为5和7,
∴EF=5,MH=7,
由正方形的性质得:∠EFG=∠EGH=∠GMH=90°,EG=GH,
∵∠FEG+∠EGF=90°,∠EGF+∠MGH=90°,
∴∠FEG=∠MGH,
在△EFG和△GMH中,
,
∴△EFG≌△GMH(AAS),
∴FG=MH=7,GM=EF=5,
∴EF2=52=25,HM2=72=49,
∴正方形B的面积为EG2=EF2+FG2=EF2+HM2=25+49=74,
故答案为:74.
12.解:带③去玻璃店,根据全等三角形的判定定理“ASA”可以配一块同样大小的三角板,
故答案为:③.
13.解:连接AB,A′B′,如图,
∵点O分别是AA′、BB′的中点,
∴OA=OA′,OB=OB′,
在△AOB和△A′OB′中,
,
∴△AOB≌△A′OB′(SAS).
∴A′B′=AB.
答:需要测量A′B′的长度,即为工件内槽宽AB.
其依据是根据SAS证明△AOB≌△A′OB′;
故答案为:SAS证明△AOB≌△A′OB′.
14.解:在△ABC和△DEC中,
,
∴△ABC≌△DCE(SAS),
∴AB=DE,
∴依据是SAS,
故答案为:SAS.
三.解答题
15.解:∵△AOB≌△ADC,
∴∠OAB=∠DAC,
∵∠OAD=∠DAB+∠OAB=80°,
∴∠BAC=∠DAB+∠DAC=80°,
在△ABC中,
∵∠ABC=∠ACB,
由三角形内角和定理知,∠ABC=∠ACB=(180°﹣80°)=50°,
又∵BC∥OA,
∴∠OAB=∠ABC=50°,
在△AOB中,
∵∠O=90°,
∴∠ABO=90°﹣50°=40°.
16.解:(1)∵△ABD≌△EBC,
∴BE=AB=2,BD=BC=3,
∵点E在BD上,
∴DE=BD﹣BE=3﹣2=1;
(2)AD与CE所在直线的位置关系为AD⊥CE,理由如下:
∵点A,B,C在同一直线上,且△ABD≌△EBC,
∴∠ABD=∠EBC=90°,
∴将△ABD绕点B顺时针方向旋转90°得到△EBC,
∴AD绕点B顺时针方向旋转90°得到EC,
∴AD⊥CE.
17.证明:∵AF=CD,点A、F、C、D在一条直线上,
∴AD+FC=DC+CF,
即AC=DF.
∵BC∥EF,
∴∠ACB=∠DFE.
在△ABC和△DEF中,
,
∴△ABC≌△DEF(SAS).
18.证明:在△AOC与△BOC中
,
∴△AOC≌△BOC(SAS).
故答案为:AO=BO.
19.证明:
∵CE∥AB(已知),
∴∠B=∠DCE (两直线平行,内错角相等).
∵D是边BC的中点(已知),
∴BD=CD;
∵AB、BC相交,
∴∠ADB=∠EDC (对顶角相等).
在△ABD和△ECD中,
,
∴△ABD≌△ECD ( ASA).
故答案为:两直线平行,内错角相等;对顶角相等;ASA.
20.证明:如图,
∵AB∥DE,
∴∠B=∠DEF.
∵BE=CF,
∴BE+EC=CF+EC.
∴BC=EF.
在△ABC与△DEF中,
.
∴△ABC≌△DEF(AAS).
21.(1)证明:∵BD⊥DE,CE⊥DE,
∴∠ADB=∠AEC=90°,
在Rt△ABD和Rt△ACE中,
∵,
∴Rt△ABD≌Rt△CAE.
∴∠DAB=∠ECA,∠DBA=∠EAC.
∵∠DAB+∠DBA=90°,∠EAC+∠ACE=90°,
∴∠BAD+∠CAE=90°.
∠BAC=180°﹣(∠BAD+∠CAE)=90°.
∴AB⊥AC.
(2)AB⊥AC.理由如下:
同(1)一样可证得Rt△ABD≌Rt△CAE.
∴∠DAB=∠ECA,∠DBA=∠EAC,
∵∠CAE+∠ECA=90°,
∴∠CAE+∠BAD=90°,即∠BAC=90°,
∴AB⊥AC.
22.证明:∵∠A=∠D=90°,AC=BD,BC=BC,
∴Rt△BAC≌Rt△CDB(HL)
∴∠ACB=∠DBC.
∴∠OCB=∠OBC.
∴OB=OC(等角对等边).
23.条件是EC=BF,
证明:∵AB=CD,
∴AB+BC=CD+BC,
∴AC=BD,
∵EA⊥AB,FD⊥AD,
∴∠A=∠D=90°,
在Rt△AEC和△Rt△DFB中
∴Rt△AEC≌△Rt△DFB(HL).
24.解:(1)∵AB⊥AD,ED⊥AD,
∴∠A=∠D=90°.
在△ABC和△DCE中,
∴△ABC≌△DCE(SAS).
∴∠B=∠DCE.
∵∠B+∠ACB=90°,
∴∠ACB+∠DCE=90°.
∴∠BCE=90°,
即BC⊥CE;
(2)∵AB⊥AD,ED⊥AD,
∴∠A=∠CDE=90°.
在△ABC和△DCE中,
∴△ABD≌△DCE(SAS).
∴∠B=∠DCE.
∵∠B+∠ADB=90°,
∴∠ADB+∠DCE=90°.
BD⊥CE.
25.(1)证明:∵CF∥AB,
∴∠A=∠ECF,
∵E为AC的中点,
∴AE=CE,
在△ADE和△CFE中,
,
∴△ADE≌△CFE(ASA),
∴DE=FE,
即E为DF的中点;
(2)解:∵CF∥AB,∠ABC=70°,
∴∠A=∠ECF,∠BCF=180°﹣∠ABC=110°,
∵AC平分∠BCF,
∴∠ECF=∠BCF=55°,
∴∠A=∠ECF=55°.
同步练习题(附答案)
一.选择题
1.如图△ABC≌△CDE,∠B=90°,点C为线段BD上一点,则∠ACE的度数为( )
A.94° B.92° C.90° D.88°
2.如图,△ABC≌△DEF,BC=5,EC=3,则CF的长为( )
A.1 B.2 C.3 D.5
3.如图,△ABC≌△A'B'C',其中∠A=37°,∠C'=23°,则∠B=( )
A.60° B.100° C.120° D.135°
4.如图,已知DB⊥AN于点B,交AE于点O,OC⊥AM于点C,且OB=OC.若∠ADB=54°,则∠OAB的大小为( )
A.15° B.18° C.22° D.30°
5.如图点F在BC,△ABC≌△AEF,AB=AE,∠B=∠E,对于以下结论不正确的是( )
A.AC=AF B.∠FAB=∠B C.EF=BC D.∠AFC=∠ACF
二.填空题
6.如图,A、F、C、D在同一条直线上,△ABC≌△DEF,AF=1,FD=3.则线段FC的长为 .
7.如图,已知△ABC≌△ADE,∠B=25°,∠E=95°,∠EAB=20°,则∠BAD的度数为 .
8.如图,直线a过正方形ABCD的顶点A,点B、D到直线a的距离分别为5、12,则正方形的周长为 .
9.如图,A,B在一水池的两侧,AB⊥BD,CD⊥BD,AC,BD交于点E,BE=DE,若CD=80m,则水池宽AB= m.
10.如图,在△ABC中,∠B=∠C=65°,BD=CE,BE=CF,则∠DEF的度数是 .
11.如图,直线l上有三个正方形A、B、C,若正方形A、C的边长分别为5和7,则正方形B的面积为 .
12.如图,由于受第18号台风“圆规”的影响,学校的某玻璃三角板摔成三块,派小明同学到玻璃店再配一块同样大小的三角板,让小明最省事的方法是带 块去.
13.如图,把两根钢条的中点连在一起,可以做到一个测量工件内槽宽的工具(长钳),在图中要测量工件内槽宽AB,只要测量A′B′长度,其依据是全等三角形判定“ ”和全等三角形对应边相等.
14.如图,公园里有一座假山,要测量假山两端A、B的距离,先在平地上取一个可以直接到达A、B的点C,分别延长AC、BC,到D、E,使CE=CB,CA=CD,连接DE,这样就可以利用三角形全等,通过测量DE的长得到假山两端A、B的距离,则这两个三角形全等的依据是 .
三.解答题
15.如图,△AOB≌△ADC,∠O=90°.已知∠ABC=∠ACB,且BC∥OA,若∠OAD=80°,求∠ABO的度数.
16.如图,点A,B,C在同一直线上,点E在BD上,且△ABD≌△EBC.
(1)若AB=2,BC=3,求DE的长;
(2)判断AD与CE所在直线的位置关系,并说明理由.
17.如图,点A、F、C、D在一条直线上,且BC=EF,BC∥EF,AF=CD.求证:△ABC≌△DEF.
18.在横线上添加一个条件,并完成证明过程:
如图,已知∠AOC=∠BOC, ,求证:△AOC≌△BOC.
19.填补下列证明过程.
如图,△ABC中,D是边BC的中点,延长AD到点E,且CE∥AB.
求证:△ABD≌△ECD.
证明:
∵CE∥AB(已知)
∴∠B=∠DCE ( ).
∵D是边BC的中点(已知)
∴ .
∵AB、BC相交
∴∠ADB=∠EDC ( ).
在△ABD和△ECD中
∴△ABD≌△ECD ( ).
20.如图,点B、E、C、F在同一直线上,点A、D在BC同侧,AB∥DE,∠A=∠D,BE=CF.求证:△ABC≌△DEF.
21.如图,在△ABC中,AB=AC,DE是过点A的直线,BD⊥DE于D,CE⊥DE于点E;
(1)若B、C在DE的同侧(如图所示)且AD=CE.求证:AB⊥AC;
(2)若B、C在DE的两侧(如图所示),且AD=CE,其他条件不变,AB与AC仍垂直吗?若是请给出证明;若不是,请说明理由.
22.已知:如图,∠A=∠D=90°,AC=BD.求证:OB=OC.
23.如图,已知点A,B,C,D在同一条直线上,EA⊥AB,FD⊥AD,AB=CD,若用“HL”证明Rt△AEC≌△Rt△DFB,需添加什么条件?并写出你的证明过程.
24.如图(1),AB⊥AD,ED⊥AD,AB=CD,AC=DE,试说明BC⊥CE的理由;
如图(2),若△ABC向右平移,使得点C移到点D,AB⊥AD,ED⊥AD,AB=CD,AD=DE,探索BD⊥CE的结论是否成立,并说明理由.
25.如图,在△ABC中,D为AB上一点,E为AC的中点,连接DE并延长至点F,连接CF,已知CF∥AB.
(1)求证:E为DF的中点;
(2)若∠ABC=70°,连接BE,BE平分∠ABC,AC平分∠BCF,求∠A的度数.
参考答案
一.选择题
1.解:∵△ABC≌△CDE,
∴∠ACB=∠CED,∠B=∠D=90°,
∵∠CED+∠ECD=90°,
∴∠ACB+∠ECD=90°,
∵∠ACB+∠ECD+∠ACE=180°,
∴∠ACE=90°.
故选:C.
2.解:∵△ABC≌△DEF,
∴EF=BC=5,
∵EC=3,
∴CF=2,
故选:B.
3.解:∵△ABC≌△A'B'C',∠C'=23°,
∴∠C=∠C′=23°,
∵∠A=37°,
∴∠B=180°﹣∠A﹣∠C=180°﹣37°﹣23°=120°,
故选:C.
4.解:∵DB⊥AN,OC⊥AM,
∴∠DBA=∠OCA=90°,
∵OB=OC,OA=OA,
∴△OAB≌△OAC(HL),
∴∠OAB=∠OAC,
∵∠ADB=54°,∠DBA=90°,
∴∠DAB=90°﹣54°=36°,
∴∠OAB=18°.
故选:B.
5.解:∵△ABC≌△AEF,
∴AC=AF,EF=BC,故选项A,C不符合题意,
∴∠AFC=∠ACF,故选项D不符合题意,
故选:B.
二.填空题
6.解:∵△ABC≌△DEF,FD=3,
∴AC=FD=3,
∵AF=1,
∴FC=AC﹣AF=3﹣1=2,
故答案为:2.
7.解:∵△ABC≌△ADE,∠B=25°,
∴∠D=∠B=25°,
∵∠E=95°,
∴∠EAD=180°﹣∠D﹣∠E=60°,
∵∠EAB=20°,
∴∠BAD=∠BAE+∠EAD=20°+60°=80°,
故答案为:80°.
8.解:∵四边形ABCD是正方形,
∴AD=AB=BC=CD,∠BAD=90°,
∵点B、D到直线a的距离分别为5、12,
∴DF⊥AF,BE⊥AE,BE=5,DF=12,
∴∠AFD=∠BEA=90°,∠ADF+∠DAF=90°,
∵∠DAF+∠BAE=90°,
∴∠ADF=∠BAE,
在Rt△AFD和Rt△BEA中,
,
∴Rt△AFD≌Rt△BEA(AAS),
∴DF=AE=12,AF=BE=5,
在Rt△BEA中,由勾股定理得:AB===13,
∴正方形ABCD的周长=4AB=52,
故答案为:52.
9.解:在△ABE和△CDE中,
,
∴△ABE≌△CDE(ASA),
∴CD=AB=80m.
故答案为:80.
10.解:在△DBE和△ECF中,
,
∴△DBE≌△ECF(SAS),
∴∠BDE=∠FEC,
∵∠DEF+∠FEC=∠B+∠BDE,
∴∠DEF=∠B=65°,
故答案为:65°.
11.解:如图,
∵正方形A,C的边长分别为5和7,
∴EF=5,MH=7,
由正方形的性质得:∠EFG=∠EGH=∠GMH=90°,EG=GH,
∵∠FEG+∠EGF=90°,∠EGF+∠MGH=90°,
∴∠FEG=∠MGH,
在△EFG和△GMH中,
,
∴△EFG≌△GMH(AAS),
∴FG=MH=7,GM=EF=5,
∴EF2=52=25,HM2=72=49,
∴正方形B的面积为EG2=EF2+FG2=EF2+HM2=25+49=74,
故答案为:74.
12.解:带③去玻璃店,根据全等三角形的判定定理“ASA”可以配一块同样大小的三角板,
故答案为:③.
13.解:连接AB,A′B′,如图,
∵点O分别是AA′、BB′的中点,
∴OA=OA′,OB=OB′,
在△AOB和△A′OB′中,
,
∴△AOB≌△A′OB′(SAS).
∴A′B′=AB.
答:需要测量A′B′的长度,即为工件内槽宽AB.
其依据是根据SAS证明△AOB≌△A′OB′;
故答案为:SAS证明△AOB≌△A′OB′.
14.解:在△ABC和△DEC中,
,
∴△ABC≌△DCE(SAS),
∴AB=DE,
∴依据是SAS,
故答案为:SAS.
三.解答题
15.解:∵△AOB≌△ADC,
∴∠OAB=∠DAC,
∵∠OAD=∠DAB+∠OAB=80°,
∴∠BAC=∠DAB+∠DAC=80°,
在△ABC中,
∵∠ABC=∠ACB,
由三角形内角和定理知,∠ABC=∠ACB=(180°﹣80°)=50°,
又∵BC∥OA,
∴∠OAB=∠ABC=50°,
在△AOB中,
∵∠O=90°,
∴∠ABO=90°﹣50°=40°.
16.解:(1)∵△ABD≌△EBC,
∴BE=AB=2,BD=BC=3,
∵点E在BD上,
∴DE=BD﹣BE=3﹣2=1;
(2)AD与CE所在直线的位置关系为AD⊥CE,理由如下:
∵点A,B,C在同一直线上,且△ABD≌△EBC,
∴∠ABD=∠EBC=90°,
∴将△ABD绕点B顺时针方向旋转90°得到△EBC,
∴AD绕点B顺时针方向旋转90°得到EC,
∴AD⊥CE.
17.证明:∵AF=CD,点A、F、C、D在一条直线上,
∴AD+FC=DC+CF,
即AC=DF.
∵BC∥EF,
∴∠ACB=∠DFE.
在△ABC和△DEF中,
,
∴△ABC≌△DEF(SAS).
18.证明:在△AOC与△BOC中
,
∴△AOC≌△BOC(SAS).
故答案为:AO=BO.
19.证明:
∵CE∥AB(已知),
∴∠B=∠DCE (两直线平行,内错角相等).
∵D是边BC的中点(已知),
∴BD=CD;
∵AB、BC相交,
∴∠ADB=∠EDC (对顶角相等).
在△ABD和△ECD中,
,
∴△ABD≌△ECD ( ASA).
故答案为:两直线平行,内错角相等;对顶角相等;ASA.
20.证明:如图,
∵AB∥DE,
∴∠B=∠DEF.
∵BE=CF,
∴BE+EC=CF+EC.
∴BC=EF.
在△ABC与△DEF中,
.
∴△ABC≌△DEF(AAS).
21.(1)证明:∵BD⊥DE,CE⊥DE,
∴∠ADB=∠AEC=90°,
在Rt△ABD和Rt△ACE中,
∵,
∴Rt△ABD≌Rt△CAE.
∴∠DAB=∠ECA,∠DBA=∠EAC.
∵∠DAB+∠DBA=90°,∠EAC+∠ACE=90°,
∴∠BAD+∠CAE=90°.
∠BAC=180°﹣(∠BAD+∠CAE)=90°.
∴AB⊥AC.
(2)AB⊥AC.理由如下:
同(1)一样可证得Rt△ABD≌Rt△CAE.
∴∠DAB=∠ECA,∠DBA=∠EAC,
∵∠CAE+∠ECA=90°,
∴∠CAE+∠BAD=90°,即∠BAC=90°,
∴AB⊥AC.
22.证明:∵∠A=∠D=90°,AC=BD,BC=BC,
∴Rt△BAC≌Rt△CDB(HL)
∴∠ACB=∠DBC.
∴∠OCB=∠OBC.
∴OB=OC(等角对等边).
23.条件是EC=BF,
证明:∵AB=CD,
∴AB+BC=CD+BC,
∴AC=BD,
∵EA⊥AB,FD⊥AD,
∴∠A=∠D=90°,
在Rt△AEC和△Rt△DFB中
∴Rt△AEC≌△Rt△DFB(HL).
24.解:(1)∵AB⊥AD,ED⊥AD,
∴∠A=∠D=90°.
在△ABC和△DCE中,
∴△ABC≌△DCE(SAS).
∴∠B=∠DCE.
∵∠B+∠ACB=90°,
∴∠ACB+∠DCE=90°.
∴∠BCE=90°,
即BC⊥CE;
(2)∵AB⊥AD,ED⊥AD,
∴∠A=∠CDE=90°.
在△ABC和△DCE中,
∴△ABD≌△DCE(SAS).
∴∠B=∠DCE.
∵∠B+∠ADB=90°,
∴∠ADB+∠DCE=90°.
BD⊥CE.
25.(1)证明:∵CF∥AB,
∴∠A=∠ECF,
∵E为AC的中点,
∴AE=CE,
在△ADE和△CFE中,
,
∴△ADE≌△CFE(ASA),
∴DE=FE,
即E为DF的中点;
(2)解:∵CF∥AB,∠ABC=70°,
∴∠A=∠ECF,∠BCF=180°﹣∠ABC=110°,
∵AC平分∠BCF,
∴∠ECF=∠BCF=55°,
∴∠A=∠ECF=55°.
