鲁教版八年级数学下册 《9.4探索三角形相似的条件》同步练习题(含解析)
文档属性
| 名称 | 鲁教版八年级数学下册 《9.4探索三角形相似的条件》同步练习题(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 267.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-05 21:20:46 | ||
图片预览


文档简介
鲁教版八年级数学下册《9.4探索三角形相似的条件》同步练习题(附答案)
一.选择题
1.下列四组图形中,不一定相似的是( )
A.两直角边之比为1:2的两个直角三角形 B.任意两个等边三角形
C.有一锐角相等的两个直角三角形 D.有一个角相等的两个等腰三角形
2.如图,每个小正方形的边长均为1,则下列图中的三角形(阴影部分)与如图中的△ABC相似的是( )
A. B. C. D.
3.在下列条件中,不能判断△ABC与△DEF相似的是( )
A.∠A=∠D,∠B=∠E B.=且∠B=∠E
C.== D.=且∠A=∠D
4.如图,已知矩形ABCD中,点E是边AD上的任一点,连接BE,过E作BE的垂线交BC延长线于点F,交边CD于点P,则图中共有相似三角形( )
A.6对 B.5对 C.4对 D.3对
5.如图,∠ABD=∠BDC=90°,∠A=∠CBD,AB=3,BD=2,则CD的长为( )
A. B. C.2 D.3
6.如图,在Rt△ABC中,∠ACB=90°,BC=3,AC=4,AB的垂直平分线DE交BC的延长线于点E,则CE的长为( )
A. B. C. D.2
二.填空题
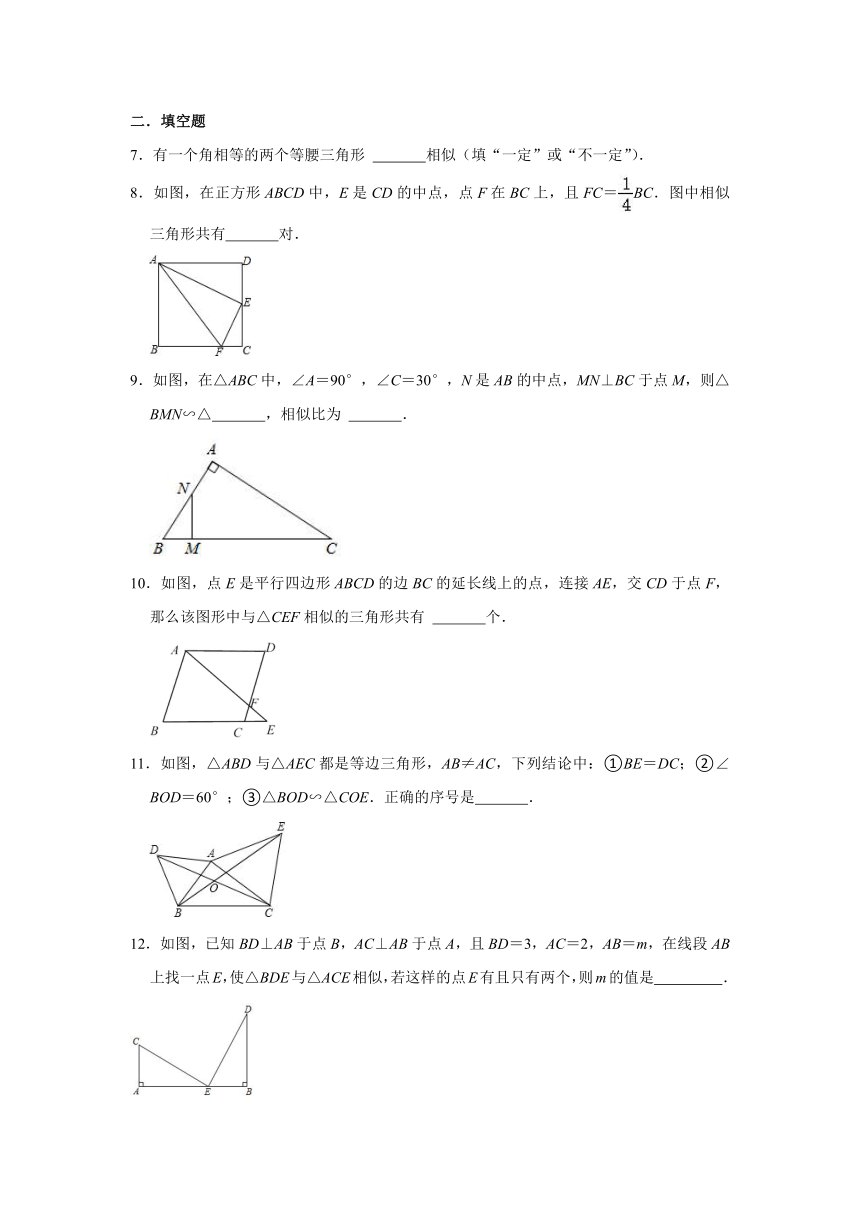
7.有一个角相等的两个等腰三角形 相似(填“一定”或“不一定”).
8.如图,在正方形ABCD中,E是CD的中点,点F在BC上,且FC=BC.图中相似三角形共有 对.
9.如图,在△ABC中,∠A=90°,∠C=30°,N是AB的中点,MN⊥BC于点M,则△BMN∽△ ,相似比为 .
10.如图,点E是平行四边形ABCD的边BC的延长线上的点,连接AE,交CD于点F,那么该图形中与△CEF相似的三角形共有 个.
11.如图,△ABD与△AEC都是等边三角形,AB≠AC,下列结论中:①BE=DC;②∠BOD=60°;③△BOD∽△COE.正确的序号是 .
12.如图,已知BD⊥AB于点B,AC⊥AB于点A,且BD=3,AC=2,AB=m,在线段AB上找一点E,使△BDE与△ACE相似,若这样的点E有且只有两个,则m的值是 .
三.解答题
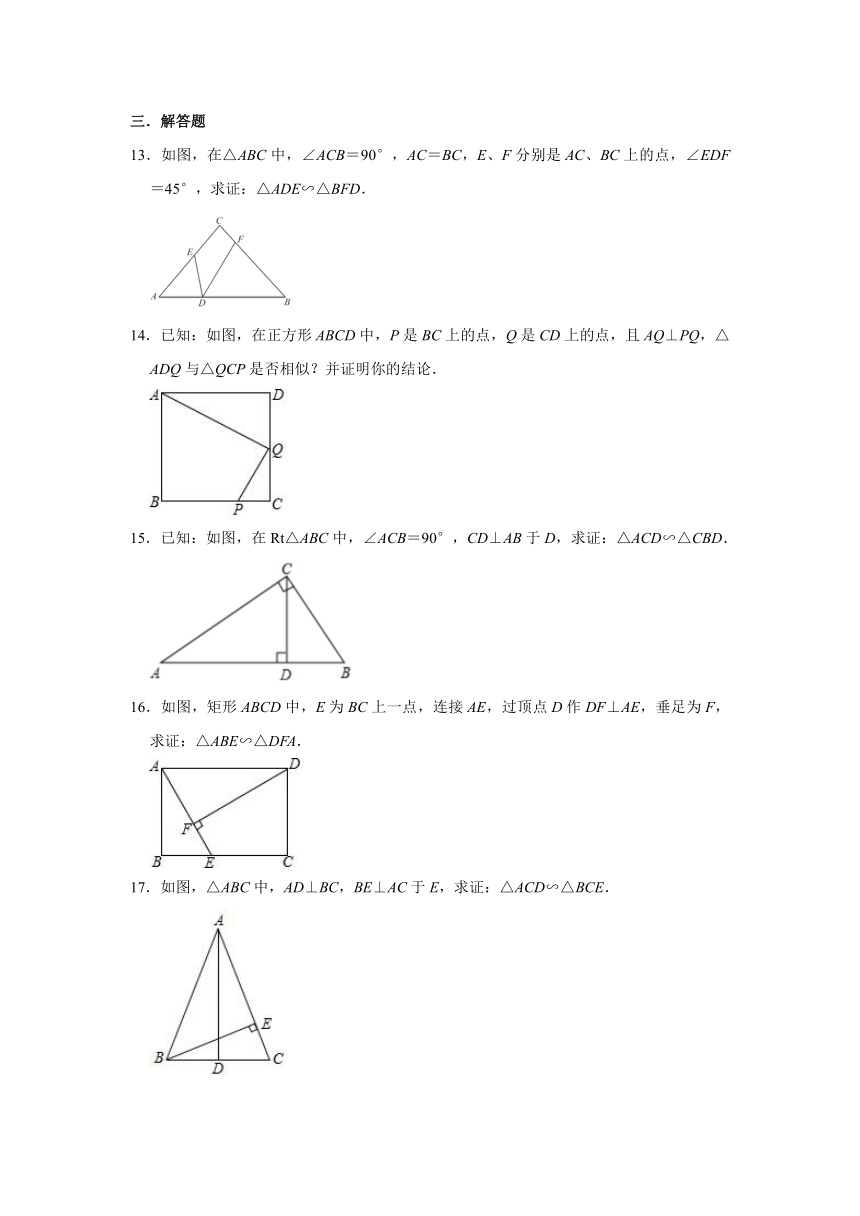
13.如图,在△ABC中,∠ACB=90°,AC=BC,E、F分别是AC、BC上的点,∠EDF=45°,求证:△ADE∽△BFD.
14.已知:如图,在正方形ABCD中,P是BC上的点,Q是CD上的点,且AQ⊥PQ,△ADQ与△QCP是否相似?并证明你的结论.
15.已知:如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,求证:△ACD∽△CBD.
16.如图,矩形ABCD中,E为BC上一点,连接AE,过顶点D作DF⊥AE,垂足为F,求证:△ABE∽△DFA.
17.如图,△ABC中,AD⊥BC,BE⊥AC于E,求证:△ACD∽△BCE.
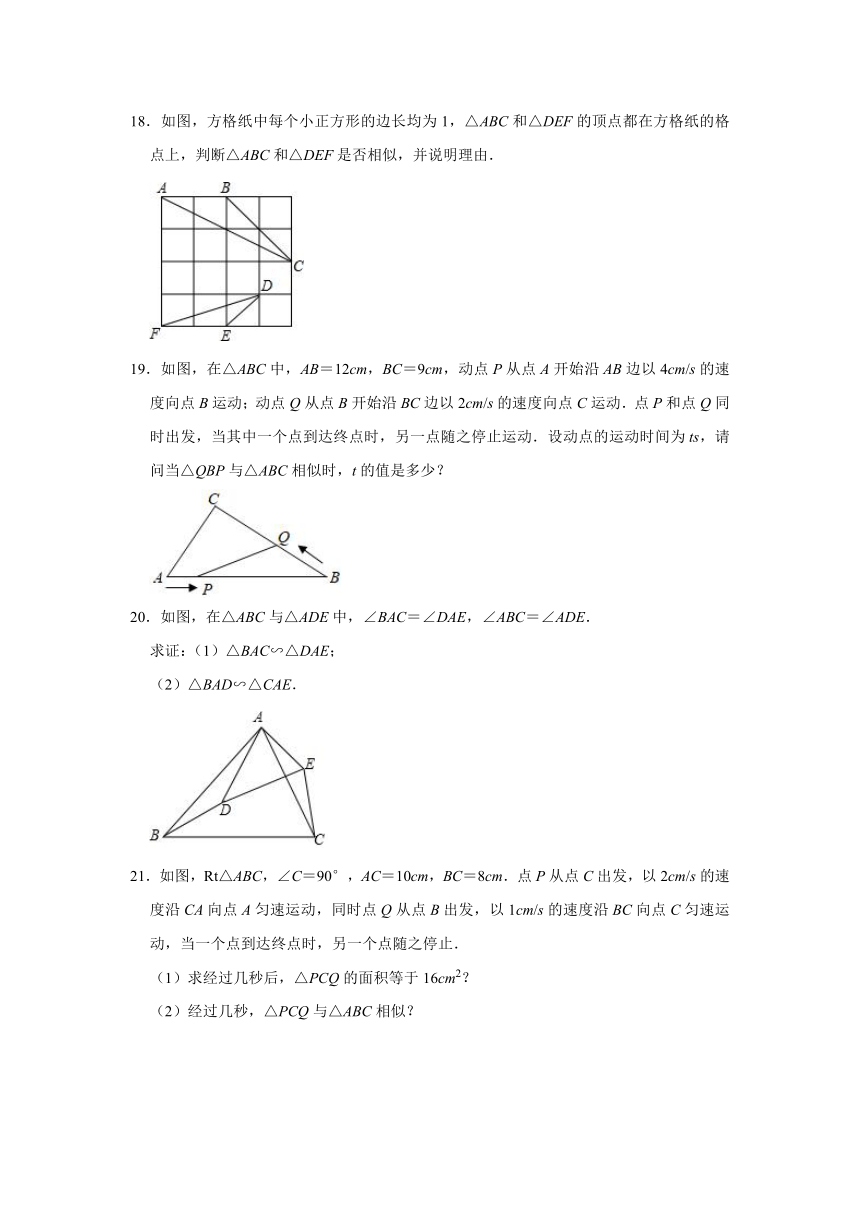
18.如图,方格纸中每个小正方形的边长均为1,△ABC和△DEF的顶点都在方格纸的格点上,判断△ABC和△DEF是否相似,并说明理由.
19.如图,在△ABC中,AB=12cm,BC=9cm,动点P从点A开始沿AB边以4cm/s的速度向点B运动;动点Q从点B开始沿BC边以2cm/s的速度向点C运动.点P和点Q同时出发,当其中一个点到达终点时,另一点随之停止运动.设动点的运动时间为ts,请问当△QBP与△ABC相似时,t的值是多少?
20.如图,在△ABC与△ADE中,∠BAC=∠DAE,∠ABC=∠ADE.
求证:(1)△BAC∽△DAE;
(2)△BAD∽△CAE.
21.如图,Rt△ABC,∠C=90°,AC=10cm,BC=8cm.点P从点C出发,以2cm/s的速度沿CA向点A匀速运动,同时点Q从点B出发,以1cm/s的速度沿BC向点C匀速运动,当一个点到达终点时,另一个点随之停止.
(1)求经过几秒后,△PCQ的面积等于16cm2?
(2)经过几秒,△PCQ与△ABC相似?
22.如图,在平面直角坐标系中,点B(12,10),过点B作x轴的垂线,垂足为A.作y轴的垂线,垂足为C点D从O出发,沿y轴正方向以每秒1个单位长度运动;点E从O出发,沿x轴正方向以每秒3个单位长度运动;点F从B出发,沿BA方向以每秒2个单位长度运动.当E点运动到点A时,三点随之停止运动.设运动时间为t.
(1)用含t的代数式分别表示点E,点F的坐标.
(2)若△ODE与以点A,E,F为顶点的三角形相似,求t的值.
参考答案
一.选择题
1.解:A、∵=,=,
∴=,即=,又∠B=∠E=90°,
∴△ABC∽△DEF,不合题意;
B、∵△ABC与△DEF都为等边三角形,
∴∠A=∠D=60°,∠B=∠E=60°,
∴△ABC∽△DEF,不合题意;
C、∵∠A=∠D,∠B=∠E=90°,
∴△ABC∽△DEF,不合题意;
D、∵AB=AC,DE=DF,
∴当∠B=∠D=30°时,∠A=120°,∠E=∠F=75°,
此时△ABC与△DEF不相似,符合题意,
故选:D.
2.解:由勾股定理得:AC==,BC=2,AB==,
∴AB:BC:AC=1::,
A、三边之比为1::2,图中的三角形(阴影部分)与△ABC不相似;
B、三边之比:1::,图中的三角形(阴影部分)与△ABC相似;
C、三边之比为::3,图中的三角形(阴影部分)与△ABC不相似;
D、三边之比为2::,图中的三角形(阴影部分)与△ABC不相似.
故选:B.
3.解:A、∠A=∠D,∠B=∠E,可以得出△ABC∽△DFE,故此选项不合题意;
B、=,且∠B=∠E,不是两边成比例且夹角相等,故此选项符合题意;
C、==,可以得出△ABC∽△DFE,故此选项不合题意;
D、=且∠A=∠D,可以得出△ABC∽△DFE,故此选项不合题意;
故选:B.
4.解:∵四边形ABCD是矩形,
∴∠A=∠ABC=∠D=∠DCB=90°,
∴∠PCF=90°,
∵BE⊥EF,
∴∠BEF=90°,
∴∠ABE+∠AEB=∠AEB+∠DEP=90°,
∴∠ABE=∠DEP,
∵AD∥BC,
∴∠DEP=∠F,
∴∠ABE=∠DEP=∠F,
∴△ABE∽△DEP∽△EFB∽△CFP,
∴图中共有相似三角形有6对,
故选:A.
5.解:∵∠ABD=∠BDC=90°,∠A=∠CBD,AB=3,BD=2,
∴△ABD∽△BDC,
∴=,即=,
解得CD=.
故选:B.
6.解:∵∠ACB=90°,BC=3,AC=4,
根据勾股定理得:AB=5,
而AB的垂直平分线DE交BC的延长线于点E,
∴∠BDE=90°,∠B=∠B,
∴△ACB∽△EDB,
∴BC:BD=AB:(BC+CE),
又∵BC=3,AC=4,AB=5,
∴3:2.5=5:(3+CE),
从而得到CE=.
解法二:连接AE.
∵DE垂直平分线段AB,
∴AE=BE,设AE=BE=x,则EC=x﹣3,
在Rt△ACE中,∵AE2=AC2+EC2,
∴x2=42+(x﹣3)2,
解得x=,
∴EC=﹣3=.
故选:B.
二.填空题
7.解:有一个角相等的两个等腰三角形不一定相似,如图,
当AB=AC,DE=DF,∠B=∠D时,
△ABC与△DEF不相似.
故答案为:不一定.
8.解:∵四边形ABCD是正方形,
∴∠D=∠C=90°,AD=DC=CB,
∵DE=CE,FC=BC,
∴DE:CF=AD:EC=2:1,
∴△ADE∽△ECF,
∴AE:EF=AD:EC,∠DAE=∠CEF,
∴AE:EF=AD:DE,
即AD:AE=DE:EF,
∵∠DAE+∠AED=90°,
∴∠CEF+∠AED=90°,
∴∠AEF=90°,
∴∠D=∠AEF,
∴△ADE∽△AEF,
∴△AEF∽△ADE∽△ECF,
即△ADE∽△ECF,△ADE∽△AEF,△AEF∽△ECF.
故答案为:3.
9.解:∵MN⊥BC,
∴∠NMB=90°,
∴∠A=∠NMB,
∵∠B=∠B,
∴△BMN∽△BAC,
∴∠BNM=∠C=30°,,
∴AB=BC;
∵N是AB的中点,
∴BN=AB;
∴BN=BC;
∴相似比为BN:BC=1:4.
故答案为:BAC;1:4.
10.解:∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,
即AD∥CE,AB∥CF,
∴△ADF∽△ECF,△ABE∽△FCE,
∴该图形中与△CEF相似的三角形共有2个,
故答案为:2.
11.解:∵△ABD、△AEC都是等边三角形,
∴AD=AB,AE=AC,∠DAB=∠CAE=60°,
∴∠DAC=∠BAC+60°,
∠BAE=∠BAC+60°,
∴∠DAC=∠BAE,
∴△DAC≌△BAE,
∴BE=DC.
∴∠ADC=∠ABE,
∵∠BOD+∠BDO+∠DBO=180°,
∴∠BOD=180°﹣∠BDO﹣∠DBO
=180°﹣(60°﹣∠ADC)﹣(60°+∠ABE)=60°,
∵△DAC≌△BAE,
∴∠ADC=∠ABE,∠AEB=∠ACD,
∵∠DBO=∠ABD+∠ABE=60°+∠ABE,∠OCE=∠ACE+∠ACO=60°+∠ACD,
∵∠ABE≠∠ACD,
∴∠DBO≠∠OCE,
∴两个三角形的最大角不相等,
∴△BOD不相似于△COE;
故答案为:①②.
12.解:∵BD⊥AB于点B,AC⊥AB,
∴∠A=∠B=90°,
当∠ACE=∠BDE时,△ACE∽△BDE,
∴==,
∴AE=BE①,
当∠ACE=∠BED时,△ACE∽△BED,
∴=,即AE×BE=AC×BD=2×3=6②,
由①②得:BE2=6,
解得:BE=3,
∴AE=2,
∴AB=AE+BE=5,即m=5;
当AE=2时,BE=3,两个三角形相似;
当AE=3时,BE=2,两个三角形全等,符合题目要求;
设AE=x,则BE=m﹣x,
∴x:3=2:(m﹣x),
整理得:x2﹣mx+6=0,
方程有唯一解时,△=m2﹣24=0,
解得:m=±2(负值舍去),
∴m=2;
当m=2时,
AE:BE=2:3时,两个三角形相似;
AE=BE=时,两个三角形相似;同样是两个点可以满足要求;
综上所述,△BDE与△ACE相似,若这样的点E有且只有两个,则m的值是5或2;
故答案为:5或2.
三.解答题
13.证明:∵∠ACB=90°,AC=BC,
∴∠A=∠B=45°,
∵∠EDB是△ADE的外角,
∴∠EDF+∠FDB=∠A+∠AED,
∵∠EDF=45°,
∴∠AED=∠FDB,
∴△ADE∽△BFD.
14.解:相似,
证明:∵四边形ABCD是正方形,
∴∠D=∠C=90°,
∵AQ⊥PQ,
∴∠DAQ+∠AQD=90°,∠PQC+∠QPC=90°,∠AQD+∠PQC=90°,
∴∠DAQ=∠PQC,
∴△ADQ∽△QCP.
15.证明:∵CD⊥AB,
∴∠ADC=∠BDC=90°,
∵∠ACB=90°,
∴∠A+∠ACD=∠ACD+∠BCD=90°,
∴∠A=∠BCD,
∴△ACD∽△CBD.
16.证明:∵四边形ABCD是矩形,
∴AD∥BC,∠B=90°,
∴∠DAE=∠AEB,
又∵∠B=∠DFA=90°,
∴△ABE∽△DFA.
17.证明:∵AD⊥BC,BE⊥AC,
∴∠BEC=∠ADC=90°,
∵∠C=∠C,
∴△ACD∽△BCE.
18.解:△ABC和△DEF相似;
理由如下:由图形可知AB=2,根据勾股定理得,BC=2,AC=2;DE=,DF=,EF=2,
∵,
∴△ABC∽△DEF.
19.解:由题意AB=12cm,BC=9cm,AP=4t,BQ=2t,则BP=(12﹣4t)cm.
当=时,两三角形相似,
∴=,
解得t=.
当=时,两三角形相似,
∴=,
解得t=,
综上所述,当△QBP与△ABC相似时,t的值是或.
20.证明:(1)∵∠BAC=∠DAE,∠ABC=∠ADE.
∴△BAC∽△DAE;
(2)∵△BAC∽△DAE,
∴,
∴,
∵∠BAC=∠DAE,
∴∠BAD=∠CAE,
∴△BAD∽△CAE.
21.解:(1)设经过x秒,△PCQ的面积等于16cm2,
2x (8﹣x)=16,
解得:x1=x2=4,
答:经过4秒后,△PCQ的面积等于16cm2;
(2)设经过t秒,△PCQ与△ABC相似,
因为∠C=∠C,
所以分为两种情况:①,
∴,
解得:t=;
②,
∴,
解得:t=;
答:经过秒或秒时,△PCQ与△ABC相似
22.解:(1)由题可得OE=3t,OD=t,BF=2t.
∵BA⊥x轴,BC⊥y轴,∠AOC=90°,
∴∠AOC=∠BAO=∠BCO=90°,
∴四边形OABC是矩形,
∴AB=OC,BC=OA.
∵B(12,10),
∴BC=OA=12,AB=OC=10,
∴AF=10﹣2t,AE=12﹣3t,
∴点E的坐标为(3t,0),点F的坐标为(12,10﹣2t);
(2)①当△ODE∽△AEF时,
则有=,
∴=,
解得t1=0(舍),t2=;
②当△ODE∽△AFE时,
则有=,
∴=,
解得t1=0(舍),t2=6.
∵点E运动到点A时,三点随之停止运动,
∴3t≤12,
∴t≤4.
∵6>4,
∴t=6舍去,
综上所述:t的值为.
一.选择题
1.下列四组图形中,不一定相似的是( )
A.两直角边之比为1:2的两个直角三角形 B.任意两个等边三角形
C.有一锐角相等的两个直角三角形 D.有一个角相等的两个等腰三角形
2.如图,每个小正方形的边长均为1,则下列图中的三角形(阴影部分)与如图中的△ABC相似的是( )
A. B. C. D.
3.在下列条件中,不能判断△ABC与△DEF相似的是( )
A.∠A=∠D,∠B=∠E B.=且∠B=∠E
C.== D.=且∠A=∠D
4.如图,已知矩形ABCD中,点E是边AD上的任一点,连接BE,过E作BE的垂线交BC延长线于点F,交边CD于点P,则图中共有相似三角形( )
A.6对 B.5对 C.4对 D.3对
5.如图,∠ABD=∠BDC=90°,∠A=∠CBD,AB=3,BD=2,则CD的长为( )
A. B. C.2 D.3
6.如图,在Rt△ABC中,∠ACB=90°,BC=3,AC=4,AB的垂直平分线DE交BC的延长线于点E,则CE的长为( )
A. B. C. D.2
二.填空题
7.有一个角相等的两个等腰三角形 相似(填“一定”或“不一定”).
8.如图,在正方形ABCD中,E是CD的中点,点F在BC上,且FC=BC.图中相似三角形共有 对.
9.如图,在△ABC中,∠A=90°,∠C=30°,N是AB的中点,MN⊥BC于点M,则△BMN∽△ ,相似比为 .
10.如图,点E是平行四边形ABCD的边BC的延长线上的点,连接AE,交CD于点F,那么该图形中与△CEF相似的三角形共有 个.
11.如图,△ABD与△AEC都是等边三角形,AB≠AC,下列结论中:①BE=DC;②∠BOD=60°;③△BOD∽△COE.正确的序号是 .
12.如图,已知BD⊥AB于点B,AC⊥AB于点A,且BD=3,AC=2,AB=m,在线段AB上找一点E,使△BDE与△ACE相似,若这样的点E有且只有两个,则m的值是 .
三.解答题
13.如图,在△ABC中,∠ACB=90°,AC=BC,E、F分别是AC、BC上的点,∠EDF=45°,求证:△ADE∽△BFD.
14.已知:如图,在正方形ABCD中,P是BC上的点,Q是CD上的点,且AQ⊥PQ,△ADQ与△QCP是否相似?并证明你的结论.
15.已知:如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,求证:△ACD∽△CBD.
16.如图,矩形ABCD中,E为BC上一点,连接AE,过顶点D作DF⊥AE,垂足为F,求证:△ABE∽△DFA.
17.如图,△ABC中,AD⊥BC,BE⊥AC于E,求证:△ACD∽△BCE.
18.如图,方格纸中每个小正方形的边长均为1,△ABC和△DEF的顶点都在方格纸的格点上,判断△ABC和△DEF是否相似,并说明理由.
19.如图,在△ABC中,AB=12cm,BC=9cm,动点P从点A开始沿AB边以4cm/s的速度向点B运动;动点Q从点B开始沿BC边以2cm/s的速度向点C运动.点P和点Q同时出发,当其中一个点到达终点时,另一点随之停止运动.设动点的运动时间为ts,请问当△QBP与△ABC相似时,t的值是多少?
20.如图,在△ABC与△ADE中,∠BAC=∠DAE,∠ABC=∠ADE.
求证:(1)△BAC∽△DAE;
(2)△BAD∽△CAE.
21.如图,Rt△ABC,∠C=90°,AC=10cm,BC=8cm.点P从点C出发,以2cm/s的速度沿CA向点A匀速运动,同时点Q从点B出发,以1cm/s的速度沿BC向点C匀速运动,当一个点到达终点时,另一个点随之停止.
(1)求经过几秒后,△PCQ的面积等于16cm2?
(2)经过几秒,△PCQ与△ABC相似?
22.如图,在平面直角坐标系中,点B(12,10),过点B作x轴的垂线,垂足为A.作y轴的垂线,垂足为C点D从O出发,沿y轴正方向以每秒1个单位长度运动;点E从O出发,沿x轴正方向以每秒3个单位长度运动;点F从B出发,沿BA方向以每秒2个单位长度运动.当E点运动到点A时,三点随之停止运动.设运动时间为t.
(1)用含t的代数式分别表示点E,点F的坐标.
(2)若△ODE与以点A,E,F为顶点的三角形相似,求t的值.
参考答案
一.选择题
1.解:A、∵=,=,
∴=,即=,又∠B=∠E=90°,
∴△ABC∽△DEF,不合题意;
B、∵△ABC与△DEF都为等边三角形,
∴∠A=∠D=60°,∠B=∠E=60°,
∴△ABC∽△DEF,不合题意;
C、∵∠A=∠D,∠B=∠E=90°,
∴△ABC∽△DEF,不合题意;
D、∵AB=AC,DE=DF,
∴当∠B=∠D=30°时,∠A=120°,∠E=∠F=75°,
此时△ABC与△DEF不相似,符合题意,
故选:D.
2.解:由勾股定理得:AC==,BC=2,AB==,
∴AB:BC:AC=1::,
A、三边之比为1::2,图中的三角形(阴影部分)与△ABC不相似;
B、三边之比:1::,图中的三角形(阴影部分)与△ABC相似;
C、三边之比为::3,图中的三角形(阴影部分)与△ABC不相似;
D、三边之比为2::,图中的三角形(阴影部分)与△ABC不相似.
故选:B.
3.解:A、∠A=∠D,∠B=∠E,可以得出△ABC∽△DFE,故此选项不合题意;
B、=,且∠B=∠E,不是两边成比例且夹角相等,故此选项符合题意;
C、==,可以得出△ABC∽△DFE,故此选项不合题意;
D、=且∠A=∠D,可以得出△ABC∽△DFE,故此选项不合题意;
故选:B.
4.解:∵四边形ABCD是矩形,
∴∠A=∠ABC=∠D=∠DCB=90°,
∴∠PCF=90°,
∵BE⊥EF,
∴∠BEF=90°,
∴∠ABE+∠AEB=∠AEB+∠DEP=90°,
∴∠ABE=∠DEP,
∵AD∥BC,
∴∠DEP=∠F,
∴∠ABE=∠DEP=∠F,
∴△ABE∽△DEP∽△EFB∽△CFP,
∴图中共有相似三角形有6对,
故选:A.
5.解:∵∠ABD=∠BDC=90°,∠A=∠CBD,AB=3,BD=2,
∴△ABD∽△BDC,
∴=,即=,
解得CD=.
故选:B.
6.解:∵∠ACB=90°,BC=3,AC=4,
根据勾股定理得:AB=5,
而AB的垂直平分线DE交BC的延长线于点E,
∴∠BDE=90°,∠B=∠B,
∴△ACB∽△EDB,
∴BC:BD=AB:(BC+CE),
又∵BC=3,AC=4,AB=5,
∴3:2.5=5:(3+CE),
从而得到CE=.
解法二:连接AE.
∵DE垂直平分线段AB,
∴AE=BE,设AE=BE=x,则EC=x﹣3,
在Rt△ACE中,∵AE2=AC2+EC2,
∴x2=42+(x﹣3)2,
解得x=,
∴EC=﹣3=.
故选:B.
二.填空题
7.解:有一个角相等的两个等腰三角形不一定相似,如图,
当AB=AC,DE=DF,∠B=∠D时,
△ABC与△DEF不相似.
故答案为:不一定.
8.解:∵四边形ABCD是正方形,
∴∠D=∠C=90°,AD=DC=CB,
∵DE=CE,FC=BC,
∴DE:CF=AD:EC=2:1,
∴△ADE∽△ECF,
∴AE:EF=AD:EC,∠DAE=∠CEF,
∴AE:EF=AD:DE,
即AD:AE=DE:EF,
∵∠DAE+∠AED=90°,
∴∠CEF+∠AED=90°,
∴∠AEF=90°,
∴∠D=∠AEF,
∴△ADE∽△AEF,
∴△AEF∽△ADE∽△ECF,
即△ADE∽△ECF,△ADE∽△AEF,△AEF∽△ECF.
故答案为:3.
9.解:∵MN⊥BC,
∴∠NMB=90°,
∴∠A=∠NMB,
∵∠B=∠B,
∴△BMN∽△BAC,
∴∠BNM=∠C=30°,,
∴AB=BC;
∵N是AB的中点,
∴BN=AB;
∴BN=BC;
∴相似比为BN:BC=1:4.
故答案为:BAC;1:4.
10.解:∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,
即AD∥CE,AB∥CF,
∴△ADF∽△ECF,△ABE∽△FCE,
∴该图形中与△CEF相似的三角形共有2个,
故答案为:2.
11.解:∵△ABD、△AEC都是等边三角形,
∴AD=AB,AE=AC,∠DAB=∠CAE=60°,
∴∠DAC=∠BAC+60°,
∠BAE=∠BAC+60°,
∴∠DAC=∠BAE,
∴△DAC≌△BAE,
∴BE=DC.
∴∠ADC=∠ABE,
∵∠BOD+∠BDO+∠DBO=180°,
∴∠BOD=180°﹣∠BDO﹣∠DBO
=180°﹣(60°﹣∠ADC)﹣(60°+∠ABE)=60°,
∵△DAC≌△BAE,
∴∠ADC=∠ABE,∠AEB=∠ACD,
∵∠DBO=∠ABD+∠ABE=60°+∠ABE,∠OCE=∠ACE+∠ACO=60°+∠ACD,
∵∠ABE≠∠ACD,
∴∠DBO≠∠OCE,
∴两个三角形的最大角不相等,
∴△BOD不相似于△COE;
故答案为:①②.
12.解:∵BD⊥AB于点B,AC⊥AB,
∴∠A=∠B=90°,
当∠ACE=∠BDE时,△ACE∽△BDE,
∴==,
∴AE=BE①,
当∠ACE=∠BED时,△ACE∽△BED,
∴=,即AE×BE=AC×BD=2×3=6②,
由①②得:BE2=6,
解得:BE=3,
∴AE=2,
∴AB=AE+BE=5,即m=5;
当AE=2时,BE=3,两个三角形相似;
当AE=3时,BE=2,两个三角形全等,符合题目要求;
设AE=x,则BE=m﹣x,
∴x:3=2:(m﹣x),
整理得:x2﹣mx+6=0,
方程有唯一解时,△=m2﹣24=0,
解得:m=±2(负值舍去),
∴m=2;
当m=2时,
AE:BE=2:3时,两个三角形相似;
AE=BE=时,两个三角形相似;同样是两个点可以满足要求;
综上所述,△BDE与△ACE相似,若这样的点E有且只有两个,则m的值是5或2;
故答案为:5或2.
三.解答题
13.证明:∵∠ACB=90°,AC=BC,
∴∠A=∠B=45°,
∵∠EDB是△ADE的外角,
∴∠EDF+∠FDB=∠A+∠AED,
∵∠EDF=45°,
∴∠AED=∠FDB,
∴△ADE∽△BFD.
14.解:相似,
证明:∵四边形ABCD是正方形,
∴∠D=∠C=90°,
∵AQ⊥PQ,
∴∠DAQ+∠AQD=90°,∠PQC+∠QPC=90°,∠AQD+∠PQC=90°,
∴∠DAQ=∠PQC,
∴△ADQ∽△QCP.
15.证明:∵CD⊥AB,
∴∠ADC=∠BDC=90°,
∵∠ACB=90°,
∴∠A+∠ACD=∠ACD+∠BCD=90°,
∴∠A=∠BCD,
∴△ACD∽△CBD.
16.证明:∵四边形ABCD是矩形,
∴AD∥BC,∠B=90°,
∴∠DAE=∠AEB,
又∵∠B=∠DFA=90°,
∴△ABE∽△DFA.
17.证明:∵AD⊥BC,BE⊥AC,
∴∠BEC=∠ADC=90°,
∵∠C=∠C,
∴△ACD∽△BCE.
18.解:△ABC和△DEF相似;
理由如下:由图形可知AB=2,根据勾股定理得,BC=2,AC=2;DE=,DF=,EF=2,
∵,
∴△ABC∽△DEF.
19.解:由题意AB=12cm,BC=9cm,AP=4t,BQ=2t,则BP=(12﹣4t)cm.
当=时,两三角形相似,
∴=,
解得t=.
当=时,两三角形相似,
∴=,
解得t=,
综上所述,当△QBP与△ABC相似时,t的值是或.
20.证明:(1)∵∠BAC=∠DAE,∠ABC=∠ADE.
∴△BAC∽△DAE;
(2)∵△BAC∽△DAE,
∴,
∴,
∵∠BAC=∠DAE,
∴∠BAD=∠CAE,
∴△BAD∽△CAE.
21.解:(1)设经过x秒,△PCQ的面积等于16cm2,
2x (8﹣x)=16,
解得:x1=x2=4,
答:经过4秒后,△PCQ的面积等于16cm2;
(2)设经过t秒,△PCQ与△ABC相似,
因为∠C=∠C,
所以分为两种情况:①,
∴,
解得:t=;
②,
∴,
解得:t=;
答:经过秒或秒时,△PCQ与△ABC相似
22.解:(1)由题可得OE=3t,OD=t,BF=2t.
∵BA⊥x轴,BC⊥y轴,∠AOC=90°,
∴∠AOC=∠BAO=∠BCO=90°,
∴四边形OABC是矩形,
∴AB=OC,BC=OA.
∵B(12,10),
∴BC=OA=12,AB=OC=10,
∴AF=10﹣2t,AE=12﹣3t,
∴点E的坐标为(3t,0),点F的坐标为(12,10﹣2t);
(2)①当△ODE∽△AEF时,
则有=,
∴=,
解得t1=0(舍),t2=;
②当△ODE∽△AFE时,
则有=,
∴=,
解得t1=0(舍),t2=6.
∵点E运动到点A时,三点随之停止运动,
∴3t≤12,
∴t≤4.
∵6>4,
∴t=6舍去,
综上所述:t的值为.
