在试验中寻找机率[上学期]
图片预览




文档简介
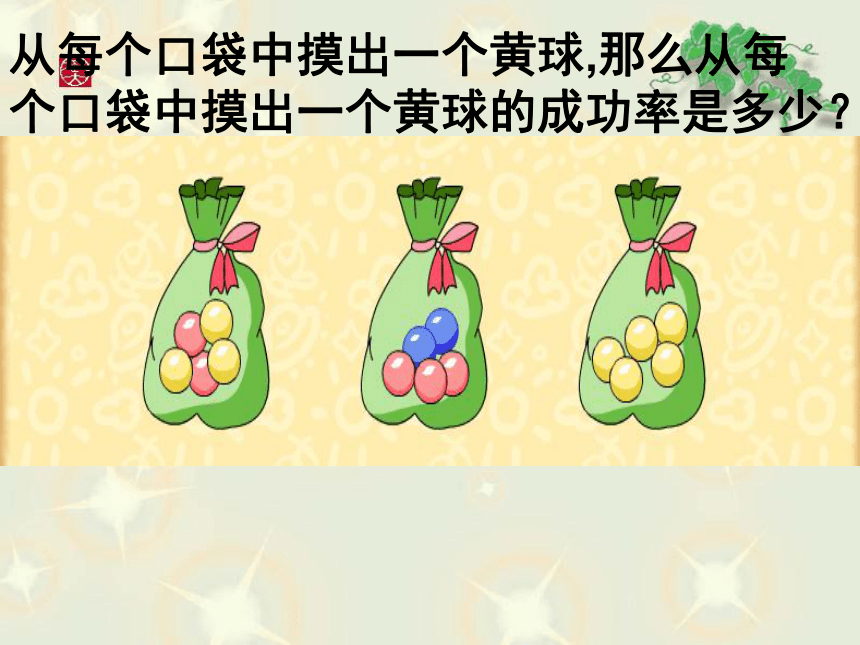
课件16张PPT。15.1在实验中寻找规律(1)从每个口袋中摸出一个黄球,那么从每个口袋中摸出一个黄球的成功率是多少? 在我们的生活中有些事情的发生是确定的,也有很多事情的发生是不确定的,是事先无法预料的。那么能否估计各种事件发生的机会的大小?
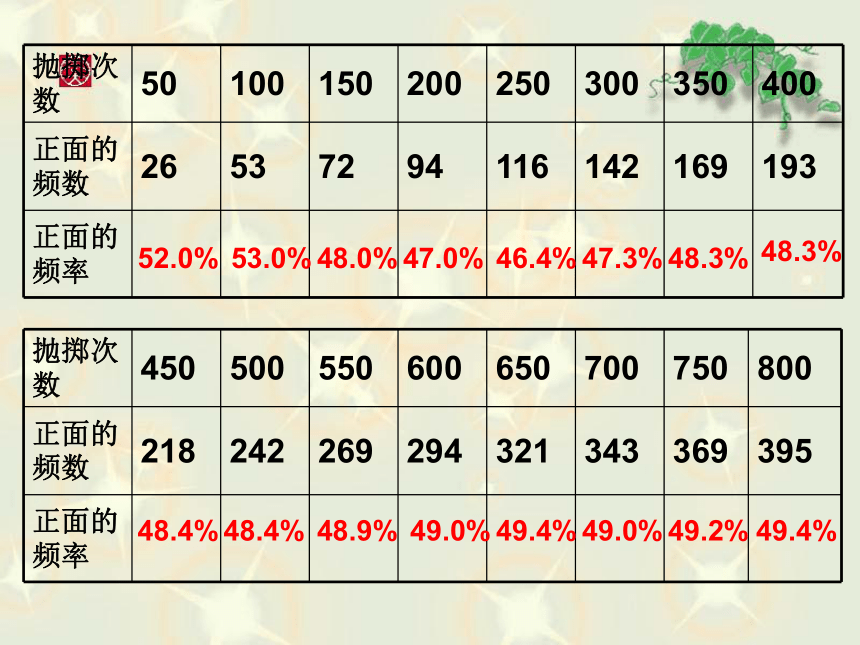
本章将运用实验的方法研究频率与机会。实验1:还记得我们做过的“抛硬币”游戏吗?下面是一位同学在”抛硬币“游戏中
获得的数据,他已经将这些数据填
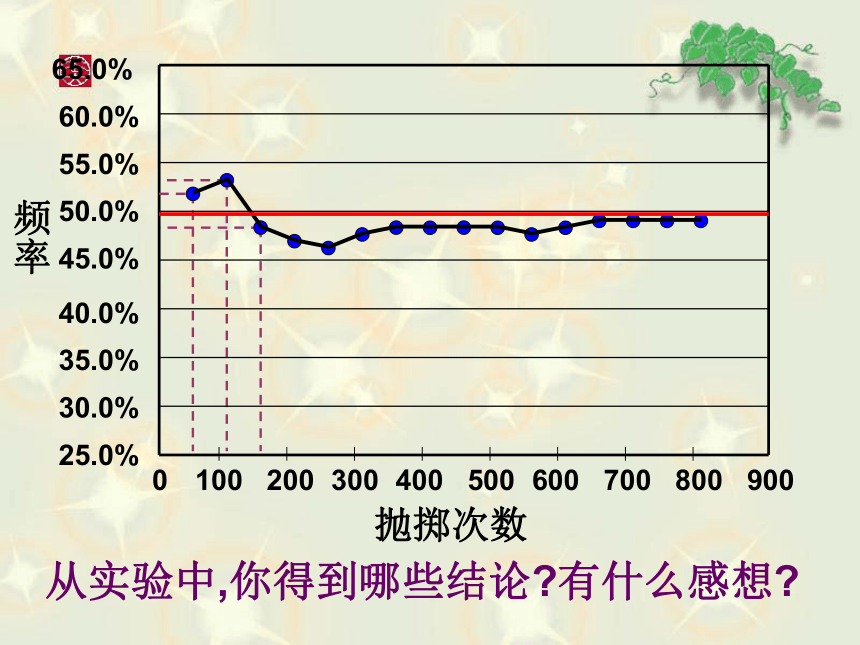
录入统计表,并绘制了折线图。52.0%48.0%47.0%46.4%47.3%48.3%48.3%53.0%48.4%48.4%48.9%49.0%49.4%49.0%49.2%49.4%010040050060070080090030020025.0%55.0%60.0%65.0%35.0%40.0%45.0%50.0%30.0%抛掷次数频率从实验中,你得到哪些结论?有什么感想?从实验1我们可以得出:虽然每次抛掷是否出现正面是不确定的,但随着实验次数的增加,出现正面的频率逐渐稳定到50%左右,我们可以估计正面出现的机会是50%历史上有很多数学家做过类似的实验: 抛掷一个硬币 数学家得到的结论也是正面出现的频率逐渐稳定是50%左右。如果改为抛掷两枚硬币,会有几种情况出现?问题:随着实验次数的增加,每种情况的频率是否也逐渐稳定到某一个数值?实验2:(1)两个正面出现的机会是四分之一
(2)两个反面出现的机会是四分之一
(3)一正一反出现的机会是二分之一。正 正
反 反实验要求:两人一组,一人边抛掷硬币边数抛掷的次数,一人记录“出现两个正面的次数”,一人记录“出现一正一反的次数”,一人配合一起观察。抛掷20次后,将记录的结果报给老师。数据汇总从实验2我们可以得出:虽然每次抛掷的结果不确定,但随着实验次数的增加,出现两个正面的频率逐渐稳定到25%左右,出现一正一反的频率逐渐稳定到50%左右,我们可以估计两个正面出现的机会是25%,一正一反出现的机会是50%结论随机事件在每次实验中发生与否具有不确定性。只要保持实验条件不变,随机事件发生的频率也会表现出规律:即随着实验次数的增加,事件发生的频率将呈现逐渐稳定的趋势。 我们可以用平稳时的频率估计这一事件在每次抛掷时发生的可能性,即机会(chance). 我思,我进步随堂练习驶向胜利的彼岸1.某人在用3枚硬币进行抛掷实验,并同时对正反面出现的结果进行统计,请问在这个实验中,总共会出现几种不同的结果( )(不按顺序)
(A)1种(B)2种(C)3种(D)4种正 正 正
正 正 反 正 反 反
反 反 反D 我思,我进步随堂练习驶向胜利的彼岸下列说法是否正确?某彩票的中奖机会是1/22,那么某人买了22张彩票,肯定有一张中奖。2. 抛掷一枚质量均匀的硬币,出现“正面”和“反面”的机会均等,因此抛1000次的话一定有500次“正”,500次“反”。 可能中奖,也可能不中奖。因为中奖是随机事件,可能发生也可能不发生。 不对,机会均为二分之一,但频率并不等同于机会,即使是多次抛掷后,频率也只可能只是与机会接近,但不一定相等。习题15.1第1题作业《探究》P79-80议一议 如果把硬币换成瓶盖,那么频率值还会逐渐稳定吗?如果是,那么稳定的数值是否同抛掷硬币的稳定值一样?
获得的数据,他已经将这些数据填
录入统计表,并绘制了折线图。52.0%48.0%47.0%46.4%47.3%48.3%48.3%53.0%48.4%48.4%48.9%49.0%49.4%49.0%49.2%49.4%010040050060070080090030020025.0%55.0%60.0%65.0%35.0%40.0%45.0%50.0%30.0%抛掷次数频率从实验中,你得到哪些结论?有什么感想?从实验1我们可以得出:虽然每次抛掷是否出现正面是不确定的,但随着实验次数的增加,出现正面的频率逐渐稳定到50%左右,我们可以估计正面出现的机会是50%历史上有很多数学家做过类似的实验: 抛掷一个硬币 数学家得到的结论也是正面出现的频率逐渐稳定是50%左右。如果改为抛掷两枚硬币,会有几种情况出现?问题:随着实验次数的增加,每种情况的频率是否也逐渐稳定到某一个数值?实验2:(1)两个正面出现的机会是四分之一
(2)两个反面出现的机会是四分之一
(3)一正一反出现的机会是二分之一。正 正
反 反实验要求:两人一组,一人边抛掷硬币边数抛掷的次数,一人记录“出现两个正面的次数”,一人记录“出现一正一反的次数”,一人配合一起观察。抛掷20次后,将记录的结果报给老师。数据汇总从实验2我们可以得出:虽然每次抛掷的结果不确定,但随着实验次数的增加,出现两个正面的频率逐渐稳定到25%左右,出现一正一反的频率逐渐稳定到50%左右,我们可以估计两个正面出现的机会是25%,一正一反出现的机会是50%结论随机事件在每次实验中发生与否具有不确定性。只要保持实验条件不变,随机事件发生的频率也会表现出规律:即随着实验次数的增加,事件发生的频率将呈现逐渐稳定的趋势。 我们可以用平稳时的频率估计这一事件在每次抛掷时发生的可能性,即机会(chance). 我思,我进步随堂练习驶向胜利的彼岸1.某人在用3枚硬币进行抛掷实验,并同时对正反面出现的结果进行统计,请问在这个实验中,总共会出现几种不同的结果( )(不按顺序)
(A)1种(B)2种(C)3种(D)4种正 正 正
正 正 反 正 反 反
反 反 反D 我思,我进步随堂练习驶向胜利的彼岸下列说法是否正确?某彩票的中奖机会是1/22,那么某人买了22张彩票,肯定有一张中奖。2. 抛掷一枚质量均匀的硬币,出现“正面”和“反面”的机会均等,因此抛1000次的话一定有500次“正”,500次“反”。 可能中奖,也可能不中奖。因为中奖是随机事件,可能发生也可能不发生。 不对,机会均为二分之一,但频率并不等同于机会,即使是多次抛掷后,频率也只可能只是与机会接近,但不一定相等。习题15.1第1题作业《探究》P79-80议一议 如果把硬币换成瓶盖,那么频率值还会逐渐稳定吗?如果是,那么稳定的数值是否同抛掷硬币的稳定值一样?
