北师大版数学六年级下册 总复习-图形的认识 第一课时 图形的认识课件(共30张ppt)
文档属性
| 名称 | 北师大版数学六年级下册 总复习-图形的认识 第一课时 图形的认识课件(共30张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-04 11:11:00 | ||
图片预览









文档简介
(共30张PPT)
总 复 习
图形的认识
第一课时 图形的认识
目 录
情景导学
1
探索与发现
2
学以致用
3
课后作业
4
情景导学
01
情景导学
等边三角形
等腰三角形
三角形
正方形
长方形
平行四边形
长方体
正方体
圆柱
圆锥
立体图形
图形
锐角三角形
直角三角形
钝角三角形
平行四边形
梯形
······
三角形
四边形
五边形
······
多边形
圆
平面图形
立体图形
······
正方形
长方形
探索与发现
02
探索与发现
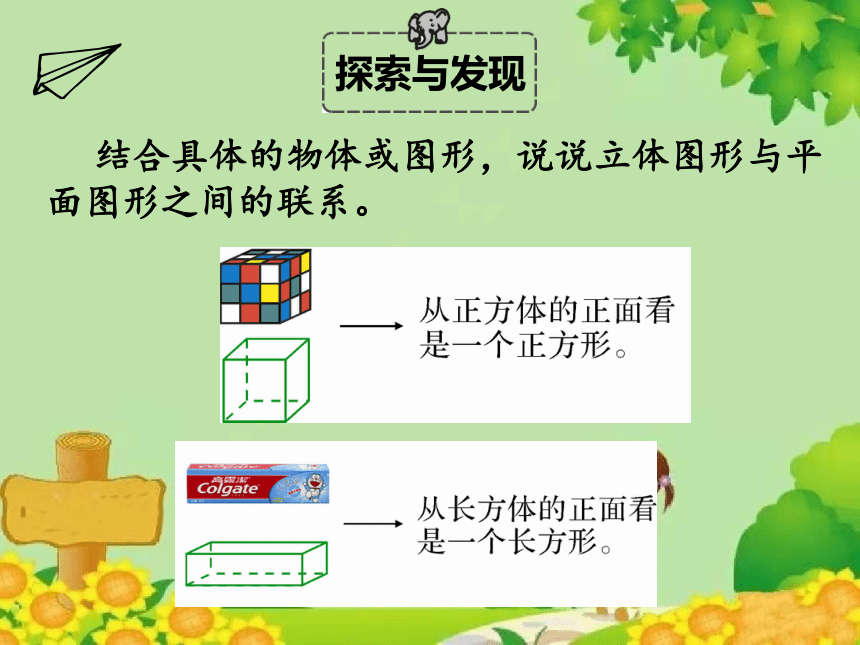
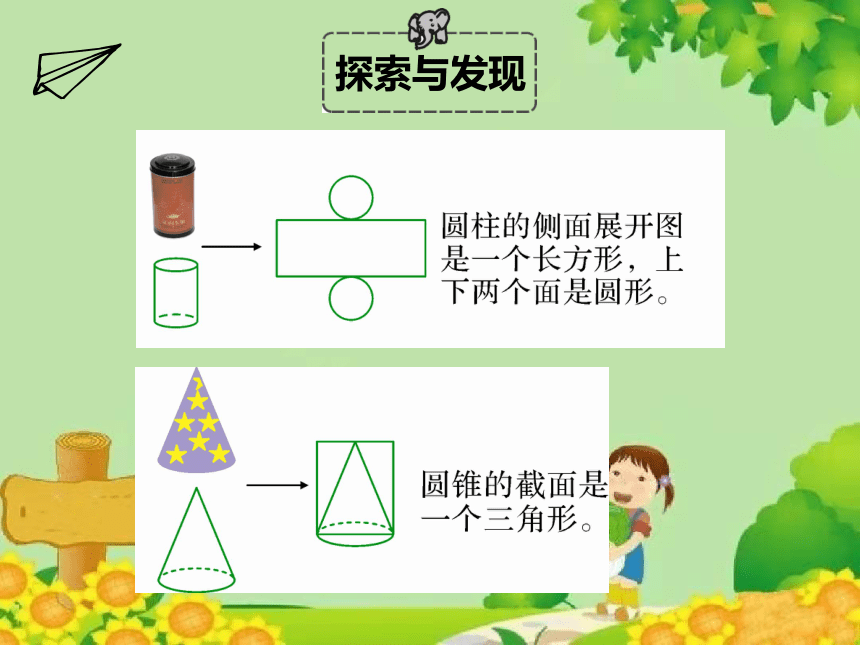
结合具体的物体或图形,说说立体图形与平面图形之间的联系。
探索与发现
探索与发现
画两条直线,想一想,在什么情况下两条直线互相垂直?在什么情况下两条直线互相平行?
探索与发现
1.垂直的意义:两条直线相交成直角时,这两条直线互相垂直,其中一条直线叫作另一条直线的垂线,这两条直线的交点叫作垂足。
探索与发现
2.平行的意义:在同一平面内,不相交的两条直线叫作平行线。同一平面内的两条直线不是相交,就是平行。两条平行线之间的距离处处相等。
探索与发现
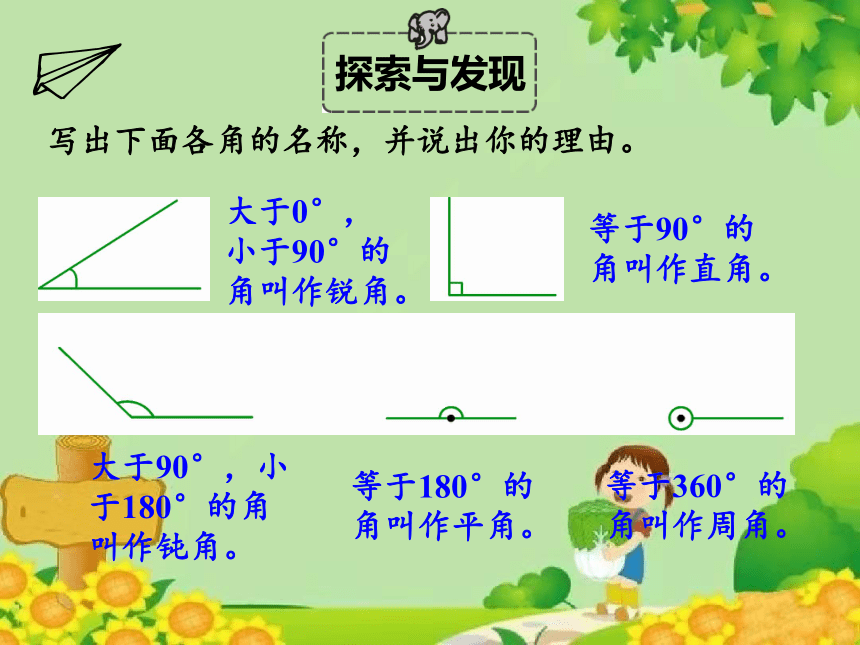
写出下面各角的名称,并说出你的理由。
大于0°,小于90°的角叫作锐角。
等于90°的角叫作直角。
大于90°,小于180°的角叫作钝角。
等于180°的角叫作平角。
等于360°的角叫作周角。
探索与发现
我们学过哪些平面图形?分别说出这些平面图形的特点,并尝试验证。
探索与发现
探索与发现
举例说明平面图形的特点在生活中的应用。
三角形的房梁架利用三角形的稳定性。
拉闸门利用平行四边形易变形的特点。
圆形的车轮、井盖等利用圆的圆心到圆上的距离处处相等的特点。
探索与发现
一个三角形可能有两个直角吗?与同伴交流你的理由。
三角形不可能有两个直角,因为一个三角形有3个角,3个角的和是180°,如果有两个直角,即90°+90°=180°,那么第3个角就不存在,没有3个角就不能叫作三角形,因此一个三角形不可能有两个直角。
探索与发现
分别说出已学过的立体图形的特点,并尝试验证。
探索与发现
观察下面用4个正方体搭成的图形,并填一填。
③
②⑤
①④
学以致用
03
学以致用
①
②
③
④
⑤
⑥
①和②互相平行。
③、④、⑤和⑥俩俩互相平行。
互相垂直:
①
②
③
④
⑤
①、 ②和⑤俩俩互相平行。
互相垂直:
①
②
③
④
①、 ②和④俩俩互相平行。
互相垂直:
①和③ 、①和⑤
②和④、②和⑥。
①和③ 、 ②和④
③和⑤、④和⑤。
①和③ 、 ②和③
③和④。
学以致用
cm
答:点A到直线BC的距离是1.5cm。
学以致用
长方形
平行四边形
梯形
学以致用
1800-400-800=
600
600
1800-900-300=
600
600
1800-600-600=
600
600
900-300=
600
或:
或:
等边三角形的
三个内角都是
600。
学以致用
学以致用
6 cm
3 cm
4 cm
3 cm
6 cm
4 cm
6 cm
4 cm
学以致用
cm
cm
学以致用
学以致用
答:①⑤是正方体的展开图。
学以致用
②号正方体的前面、后面和下面是红色。
③号正方体的前面、后面、下面和右面是红色。
⑤号正方体的前面、后面、上面和右面是红色。
④号正方体的前面、后面、上面和左面是红色。
①号正方体的前面、后面、上面、下面和左面是红色。
①
②
③
④
⑤
1
3
1
课后作业
04
感 谢 观 看
总 复 习
图形的认识
第一课时 图形的认识
目 录
情景导学
1
探索与发现
2
学以致用
3
课后作业
4
情景导学
01
情景导学
等边三角形
等腰三角形
三角形
正方形
长方形
平行四边形
长方体
正方体
圆柱
圆锥
立体图形
图形
锐角三角形
直角三角形
钝角三角形
平行四边形
梯形
······
三角形
四边形
五边形
······
多边形
圆
平面图形
立体图形
······
正方形
长方形
探索与发现
02
探索与发现
结合具体的物体或图形,说说立体图形与平面图形之间的联系。
探索与发现
探索与发现
画两条直线,想一想,在什么情况下两条直线互相垂直?在什么情况下两条直线互相平行?
探索与发现
1.垂直的意义:两条直线相交成直角时,这两条直线互相垂直,其中一条直线叫作另一条直线的垂线,这两条直线的交点叫作垂足。
探索与发现
2.平行的意义:在同一平面内,不相交的两条直线叫作平行线。同一平面内的两条直线不是相交,就是平行。两条平行线之间的距离处处相等。
探索与发现
写出下面各角的名称,并说出你的理由。
大于0°,小于90°的角叫作锐角。
等于90°的角叫作直角。
大于90°,小于180°的角叫作钝角。
等于180°的角叫作平角。
等于360°的角叫作周角。
探索与发现
我们学过哪些平面图形?分别说出这些平面图形的特点,并尝试验证。
探索与发现
探索与发现
举例说明平面图形的特点在生活中的应用。
三角形的房梁架利用三角形的稳定性。
拉闸门利用平行四边形易变形的特点。
圆形的车轮、井盖等利用圆的圆心到圆上的距离处处相等的特点。
探索与发现
一个三角形可能有两个直角吗?与同伴交流你的理由。
三角形不可能有两个直角,因为一个三角形有3个角,3个角的和是180°,如果有两个直角,即90°+90°=180°,那么第3个角就不存在,没有3个角就不能叫作三角形,因此一个三角形不可能有两个直角。
探索与发现
分别说出已学过的立体图形的特点,并尝试验证。
探索与发现
观察下面用4个正方体搭成的图形,并填一填。
③
②⑤
①④
学以致用
03
学以致用
①
②
③
④
⑤
⑥
①和②互相平行。
③、④、⑤和⑥俩俩互相平行。
互相垂直:
①
②
③
④
⑤
①、 ②和⑤俩俩互相平行。
互相垂直:
①
②
③
④
①、 ②和④俩俩互相平行。
互相垂直:
①和③ 、①和⑤
②和④、②和⑥。
①和③ 、 ②和④
③和⑤、④和⑤。
①和③ 、 ②和③
③和④。
学以致用
cm
答:点A到直线BC的距离是1.5cm。
学以致用
长方形
平行四边形
梯形
学以致用
1800-400-800=
600
600
1800-900-300=
600
600
1800-600-600=
600
600
900-300=
600
或:
或:
等边三角形的
三个内角都是
600。
学以致用
学以致用
6 cm
3 cm
4 cm
3 cm
6 cm
4 cm
6 cm
4 cm
学以致用
cm
cm
学以致用
学以致用
答:①⑤是正方体的展开图。
学以致用
②号正方体的前面、后面和下面是红色。
③号正方体的前面、后面、下面和右面是红色。
⑤号正方体的前面、后面、上面和右面是红色。
④号正方体的前面、后面、上面和左面是红色。
①号正方体的前面、后面、上面、下面和左面是红色。
①
②
③
④
⑤
1
3
1
课后作业
04
感 谢 观 看
