钉尖触地的机率[上学期]

课件15张PPT。钉尖触地的机会1.发现问题3.解决问题的方法4.抛图钉实验5.实验条件研究用频率估计机会的大小6.结论7.课堂练习及作业2.提出问题 发现问题： 有的问题,即使不做实验,也可以设法推测出事件发生的机会,例如抛掷一枚硬币出现正面朝上的机会和出现反面朝上的机会都是1/2。
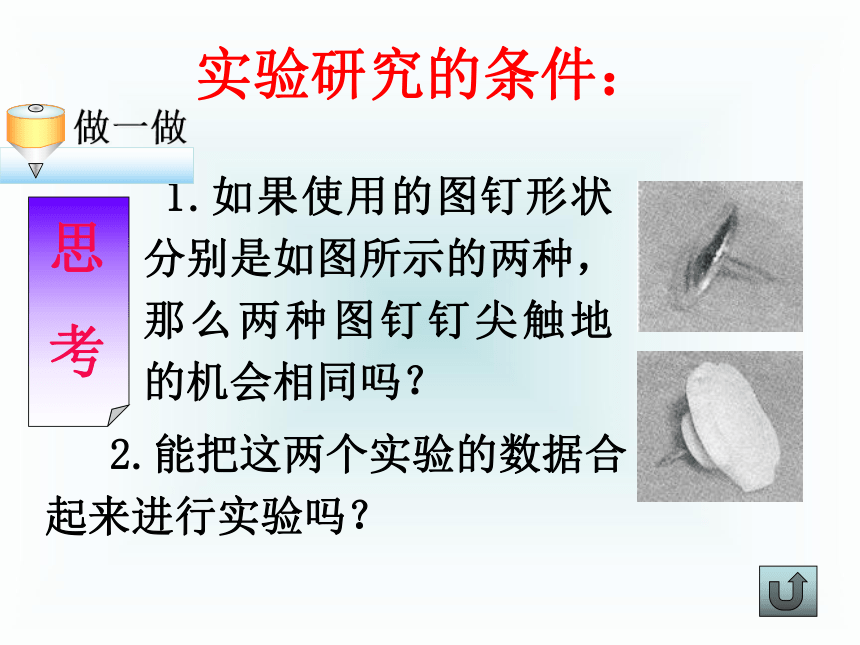
但有的问题根本无法从理性的角度预测出机会的大小,就必须通过实验的方法.实验是估计机会大小的一种重要方法。 1.一枚图钉被抛起后钉尖触地的机会有多大？问题的提出： 2.你能够预先推测出钉尖触地的机会有多大吗？ 我们可以通过实验，观察某事件出现的频率，当频率值逐渐稳定时，这个值就可以作为我们对该事件发生机会的估计。解决问题的方法：抛图钉实验： 1.通过小组合作，记录多次重复抛掷图钉后出现钉尖触地的频数和频率。 2.填出统计表，绘制折线图。 1.如果使用的图钉形状分别是如图所示的两种，那么两种图钉钉尖触地的机会相同吗？ 2.能把这两个实验的数据合
起来进行实验吗？实验研究的条件： 1.通过实验的方法用频率估计机会的大小，必须要求实验是在相同条件下进行的。比如，以同样方式抛掷同一种图钉。
相同的条件下，实验次数越多，就越有可能得到较好的估计值，但不同小组实验所得的估计值也并不一定相同。 那么，总共要做多少次实验才能认为得出的结果比较可靠呢？请看某班同学的实验及统计表和折线图.50.0%41.7%43.1%44.0%43.8%44.6%45.6%46.3%45.3%45.8%44.5%45.6%43.8%44.3%44.8%44.5%44.9%45.7%45.8%45.6%45.6%45.8%46.4%45.6%抛掷次数频率从实验中,你得到哪些结论?有什么感想?从实验我们可以得出： 当实验进行到720次以后,所得频率值就在46%上下浮动,且浮动得幅度不超过0.5%,我们可以取46%作为这个事件发生机会得估计值。 可见，总共要做多少次实验才能得到可靠的估计值主要取决于我们想要达到的精确程度，观察频率折线图的变化趋势再结合理性的分析。1、通过实验的方法，用频率估计机会的大小，必须在相同的实验条件下进行。2、实验次数越多，得到的估计值就越好。3、不同小组实验得出的估计值可能不相
同。4、要获得大量数据，最好借助集体的力
量或计算机。小结：练习巩固 某同学为了研究可乐瓶盖抛起后落
地时，正面朝上的机会，做了实验。 上述实验中，会遇到各种情况，你
认为下列说法正确吗？谈谈你的看法。1、一位同学说：我只做了10次实验就可
以得出瓶盖抛起后落地时“正面朝上”
的机会是50%. （ ）×2、一位同学用的可乐瓶盖不小心滚得
不见了，这时他用啤酒瓶盖代替做
了实验，你认为他的做法对吗？（ ）×3、一位同学提了个意见，用一个瓶盖抛
太慢了，可用5个相同型号的可乐瓶
盖同时抛，每抛一次就相当于用一个
抛了5次，这样提高了实验速度。（ ）√教材p.108

习题15.2 第 1、2 题。 作业