函数复习[下学期]

课件16张PPT。函数复习歌山一中 张大军xy（１）已知点P(a,b)在第四象限,则a＿０,ｂ＿０．
已知点Ｐ（－１－ｍ２，１），则点Ｐ位于
第＿＿象限．（2）已知点Ｍ（ｍ＋１，５）到ｙ轴的距离与它到ｘ轴距离相等，则ｍ的值为＿＿＿＿．
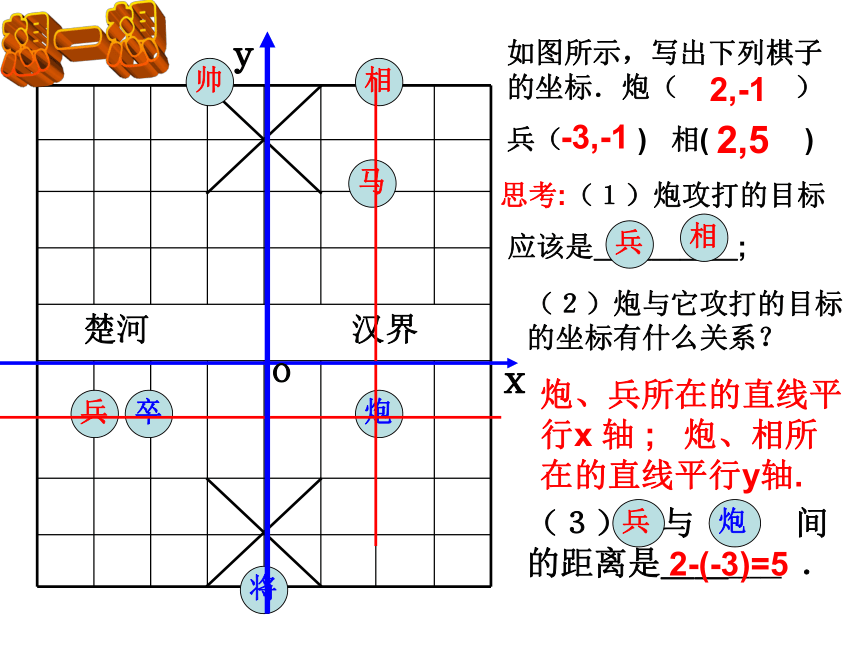
则点M位于象限的_______线上.><二用一用：角平分4或-6如图所示，写出下列棋子的坐标．炮（　　　　）
兵（　　 ) 相( )思考:（１）炮攻打的目标
应该是＿＿＿＿＿;
炮、兵所在的直线平行x 轴 ; 炮、相所在的直线平行y轴.2,-1-3,-12,5ｘｙｏ2-(-3)=5（２）炮与它攻打的目标 的坐标有什么关系？
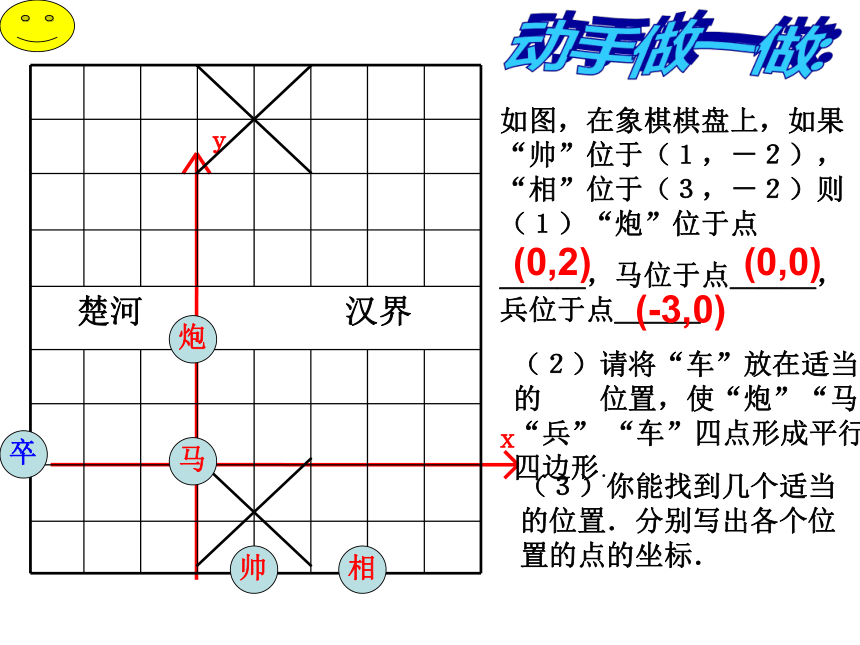
如图，在象棋棋盘上，如果“帅”位于（１，－２），“相”位于（３，－２）则（１）“炮”位于点
＿＿＿，马位于点＿＿＿，兵位于点＿＿＿
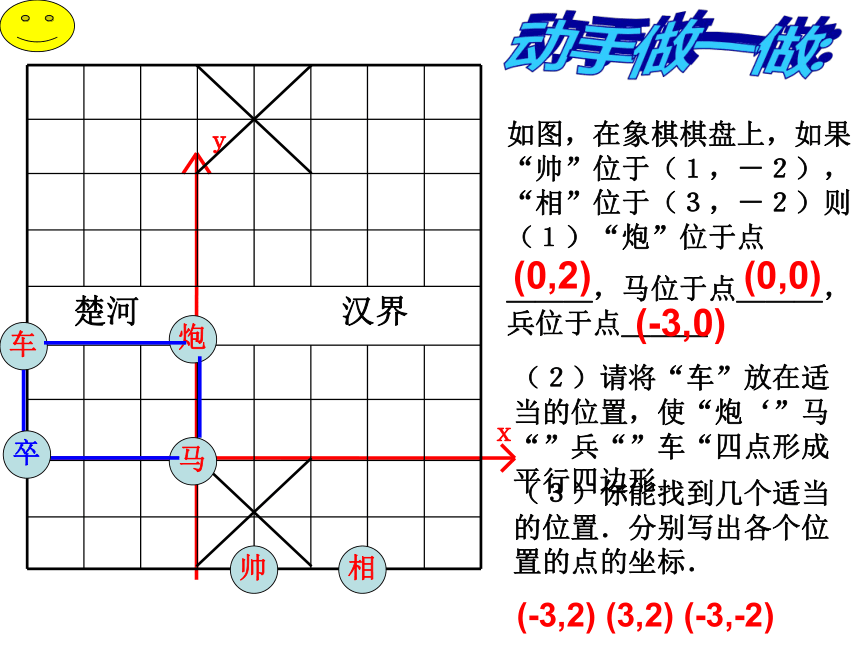
（２）请将“车”放在适当的　　位置，使“炮”“马” “兵” “车”四点形成平行四边形．（３）你能找到几个适当的位置．分别写出各个位置的点的坐标．(0,2)(0,0)(-3,0)动手做一做:如图，在象棋棋盘上，如果“帅”位于（１，－２），“相”位于（３，－２）则（１）“炮”位于点
＿＿＿，马位于点＿＿＿，兵位于点＿＿＿
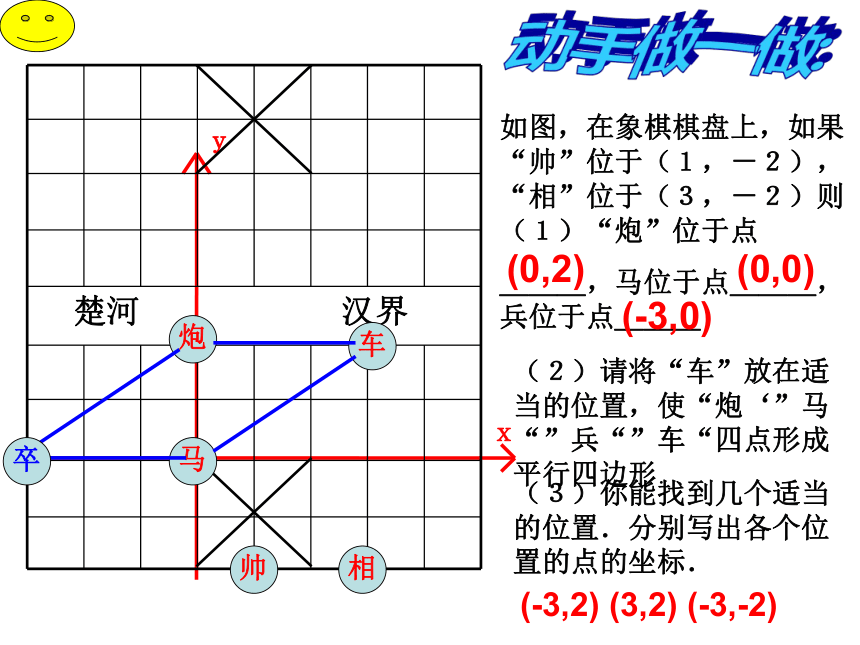
（２）请将“车”放在适当的位置，使“炮‘”马“”兵“”车“四点形成平行四边形．（３）你能找到几个适当的位置．分别写出各个位置的点的坐标．(0,2)(0,0)(-3,0)
(-3,2) (3,2) (-3,-2)
动手做一做:如图，在象棋棋盘上，如果“帅”位于（１，－２），“相”位于（３，－２）则（１）“炮”位于点
＿＿＿，马位于点＿＿＿，兵位于点＿＿＿
（２）请将“车”放在适当的位置，使“炮‘”马“”兵“”车“四点形成平行四边形．（３）你能找到几个适当的位置．分别写出各个位置的点的坐标．(-3,0)
(0,2)
(0,0)(-3,2) (3,2) (-3,-2)
动手做一做:如图，在象棋棋盘上，如果“帅”位于（１，－２），“相”位于（３，－２）则（１）“炮”位于点
＿＿＿，马位于点＿＿＿，兵位于点＿＿＿
（２）请将“车”放在适当的位置，使“炮‘”马“”兵“”车“四点形成平行四边形．（３）你能找到几个适当的位置．分别写出各个位置的点的坐标．(-3,0)
(0,2)
(0,0)(-3,2) (3,2) (-3,-2)
动手做一做:　在平面坐标系中，点Ａ，Ｂ，Ｃ的坐标分别是Ａ（－２，５）Ｂ（－３，－１）　Ｃ（１，－１），在第一象限中找一点Ｄ，使四边形ＡＢＣＤ是平行四边形，那么点Ｄ的坐标是＿＿＿＿＿．（２００５年武汉市中考题）
　深化：找出所有的Ｄ点，
并写出Ｄ点的坐标．x2) 试写出图（2）至图（4）中“A1”各顶点的坐标.3) 求出以A1、B1、O、A点组成的四边形的面积.
议一议 图（1）中的图案“A”的三个顶点的坐标分别是A（2,4）、O （0,0）、B（4，0）.经过变换：沿x轴翻折;纵坐标不变、横坐标扩大到原来的2倍;绕点O逆时针方向旋转90°，分别变成图（2）至图（4）中的相应图案。
1) ?ABC形状发生变化的是哪个图形?

4)如图（4）,你能用几种方法求四边形AB1A1O的面积?你找到的最快方法是什么?练一练：（Ａ组）
１、Ｐ（ｔ－１，ｔ＋２）在ｘ轴上，则ｔ等于 _____．
２、若点Ｑ到ｘ轴的距离为５，到ｙ轴的距离为４，
且点Ｑ在第四象限，则点Ｑ的坐标是_______.
３、点Ｐ（１，－６）关于原点对称点的坐标是___________.-2(4,- 5)(-1,6) （Ｂ组）
4、已知不同的两点Ｐ（ａ，－３）,Ｑ（５，ｂ）若直线ＰＱ平行于坐标轴，
求a、b的值。

当直线平行于ｘ轴时,b=-3,a为不等于0的任何实数;当直线平行于ｙ轴时,a=5,b为不等于0的任何实数;
6、象棋中，马沿“日”字走。如图，马（-2，-1）。试写出马走一步后到达的所有的点的坐标。并找出这些点间的关系。（Ｃ组）提高:(-3,1) (-1,1)
(-4,0) (0,0)
(-4,-2) (0,-2)
(-3,-3) (-1,-3)5、如图，在直角坐标系中，将△OAB变换成△OA1B1 ,变换成△OA2B2 ，变换成△OA3B3 。已知:
A(1，3)，A1 (2,3)，A2 (4，3)，A3 (8，3);
B(2，0)，B1 (4，0)， B2 (8，0)，B3(16，0)。
(1)　按此变换规律再将△ OA3B3变换成△OA4B4 ，那么 A4的坐标是______，B4的坐标是_____。
(2)　观察每次变换前后的三角形有何变化，找出规律.(32,0)(16,3)(2n,3)(2n+1,0)(3)　若按第（1）题找到的规律，将△OAB进行n次变换，得到△OAnBn，比较每次变换中三角形顶点有何变化，找出规律，推测An 的坐标是______,Bn的坐标是________.
C组 这堂课你愉快吗？
我们复习了……
你巩固了……
你新明白了……
……
你有什么遗憾吗?小结：