分组分解法[下学期]
图片预览


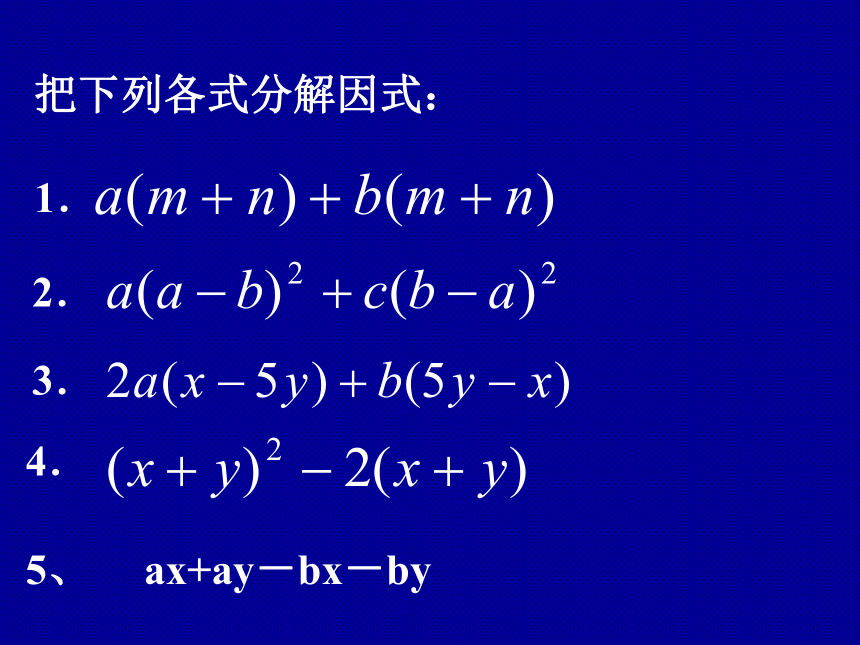




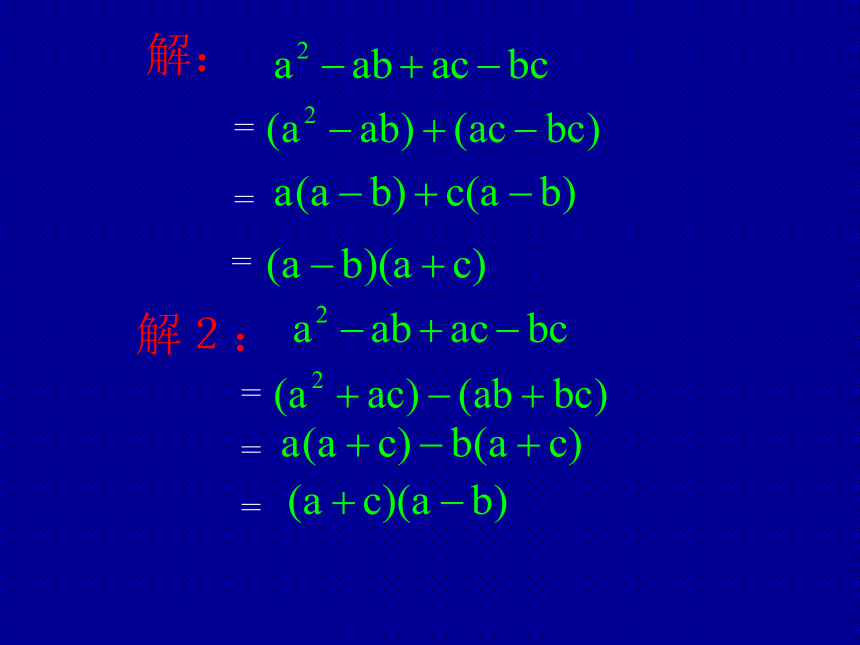

文档简介
课件20张PPT。(一)分组后能直接提公因式因式分解分 组 分 解 法在这里我们把它的前两项分成一组
并提出公因式 ; 把它的后两项分成一组,并提出
公因式 . 1.分组后能直接提公因式我们看下面这个多项式要把这个多项式分解因式,不能提公因式也不能用公式!把下列各式分解因式:
1.2.3.4.5、 ax+ay-bx-by整式乘法 (a+b)(m+n) =a(m+n)+b(m+n)=am+an+bm+bnam+an+bm+bn=a(m+n)+b(m+n)=(a+b)(m+n)因式分解定义:
这种把多项式分成几组来分解因式的方法叫分组分解法注意:如果把一个多项式的项分组并提出公因式后,它们的另一个因式正好相同,那么这个多项式就可以用分组分解法来分解因式。引例从而得到 这时候由于 与又有公因式 于是可以继续提出公因式 从而得到: 这种利用分组来分解因式的方法叫做分组分解法.从上面的说明可以看出,如果把一个多项式的项分组并提出公因式,它们的另一个因式正好相同,那么这个多项就可以用分组分解法来分解因式.
例1 把 分解因式. 分析:把这个多项式的四项按前两项与后两项分成两组,分别提出公因式 与 后,另一个因式正好都是 这样就可以继续提公因式.
解: = = = 解2: = = = 例2 把 分解因式. 分析:把这个多项式的四项按前两项与后两项分成两组,并使两组的项都按 的降幂排列,然后从两组分别提出公因式 与 ,这时另一个因式正好都是 .这样就可以继续提公因式. 解: = = = = 解2: = = =
练 习1、把下列各式分解因式:2、把下列各式分解因式: 在有公因式的前提下,按对应项系数成比例分组,或按对应项的次数成比例分组。 (1)分组;(2)在各组内提公因式;(3)在各组之间进行因式分解(4)直至完全分解分组规律:分解步骤:例3:把 分解因式.
分析:如果把这个多项式的四项按前两项与后两项分组,无法分解因式. 但如果把第一、三两项作为一组,第二、四两项作为另一组,分别提出公因式 与 后,另一个因式正好都是 解: = = = 解2:
= = = 例4:把 分解因式. 解: = = = 解2: = = = 解:原式例5 x2-x2y+xy2-x+y-y2=(x2-y2)-(x2y-xy2)-(x-y)=(x-y)(x+y)-xy(x-y)-(x-y)=(x-y)(x+y-xy-1)=(x-y)[(x-xy)+(y-1)]=(x-y)[x(1-y)-(1-y)]=(x-y)(1-y)(x-1)练 习把下列各式分解因式:把下列各式分解因式:本课小结教学重点:掌握分组分解法的分组规律和步骤。主要内容:
学习分组分解法的概念,用分组分解法分组之后,可以用提公因式的多项式进行因式分解。作业
并提出公因式 ; 把它的后两项分成一组,并提出
公因式 . 1.分组后能直接提公因式我们看下面这个多项式要把这个多项式分解因式,不能提公因式也不能用公式!把下列各式分解因式:
1.2.3.4.5、 ax+ay-bx-by整式乘法 (a+b)(m+n) =a(m+n)+b(m+n)=am+an+bm+bnam+an+bm+bn=a(m+n)+b(m+n)=(a+b)(m+n)因式分解定义:
这种把多项式分成几组来分解因式的方法叫分组分解法注意:如果把一个多项式的项分组并提出公因式后,它们的另一个因式正好相同,那么这个多项式就可以用分组分解法来分解因式。引例从而得到 这时候由于 与又有公因式 于是可以继续提出公因式 从而得到: 这种利用分组来分解因式的方法叫做分组分解法.从上面的说明可以看出,如果把一个多项式的项分组并提出公因式,它们的另一个因式正好相同,那么这个多项就可以用分组分解法来分解因式.
例1 把 分解因式. 分析:把这个多项式的四项按前两项与后两项分成两组,分别提出公因式 与 后,另一个因式正好都是 这样就可以继续提公因式.
解: = = = 解2: = = = 例2 把 分解因式. 分析:把这个多项式的四项按前两项与后两项分成两组,并使两组的项都按 的降幂排列,然后从两组分别提出公因式 与 ,这时另一个因式正好都是 .这样就可以继续提公因式. 解: = = = = 解2: = = =
练 习1、把下列各式分解因式:2、把下列各式分解因式: 在有公因式的前提下,按对应项系数成比例分组,或按对应项的次数成比例分组。 (1)分组;(2)在各组内提公因式;(3)在各组之间进行因式分解(4)直至完全分解分组规律:分解步骤:例3:把 分解因式.
分析:如果把这个多项式的四项按前两项与后两项分组,无法分解因式. 但如果把第一、三两项作为一组,第二、四两项作为另一组,分别提出公因式 与 后,另一个因式正好都是 解: = = = 解2:
= = = 例4:把 分解因式. 解: = = = 解2: = = = 解:原式例5 x2-x2y+xy2-x+y-y2=(x2-y2)-(x2y-xy2)-(x-y)=(x-y)(x+y)-xy(x-y)-(x-y)=(x-y)(x+y-xy-1)=(x-y)[(x-xy)+(y-1)]=(x-y)[x(1-y)-(1-y)]=(x-y)(1-y)(x-1)练 习把下列各式分解因式:把下列各式分解因式:本课小结教学重点:掌握分组分解法的分组规律和步骤。主要内容:
学习分组分解法的概念,用分组分解法分组之后,可以用提公因式的多项式进行因式分解。作业
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
