三角形中位线[上学期]

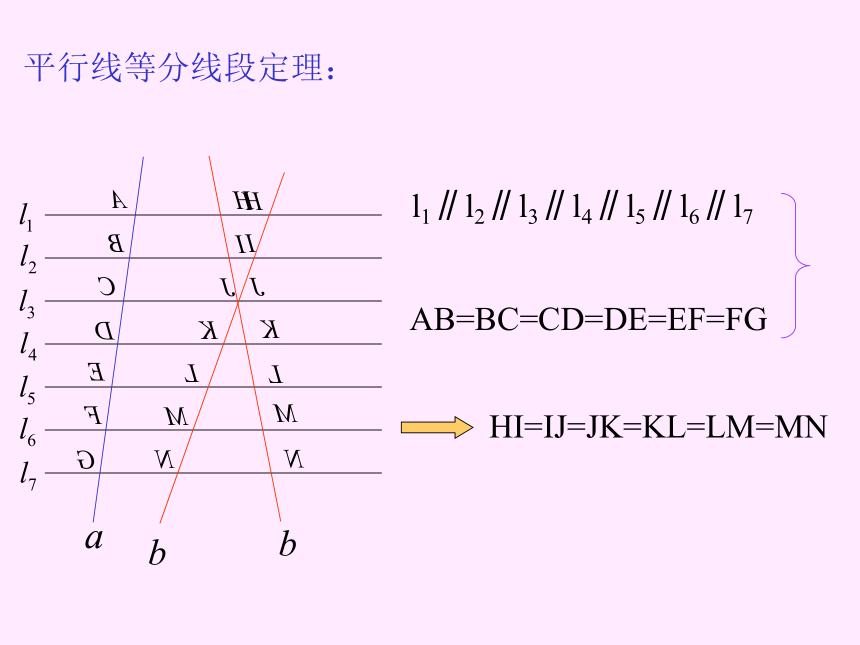
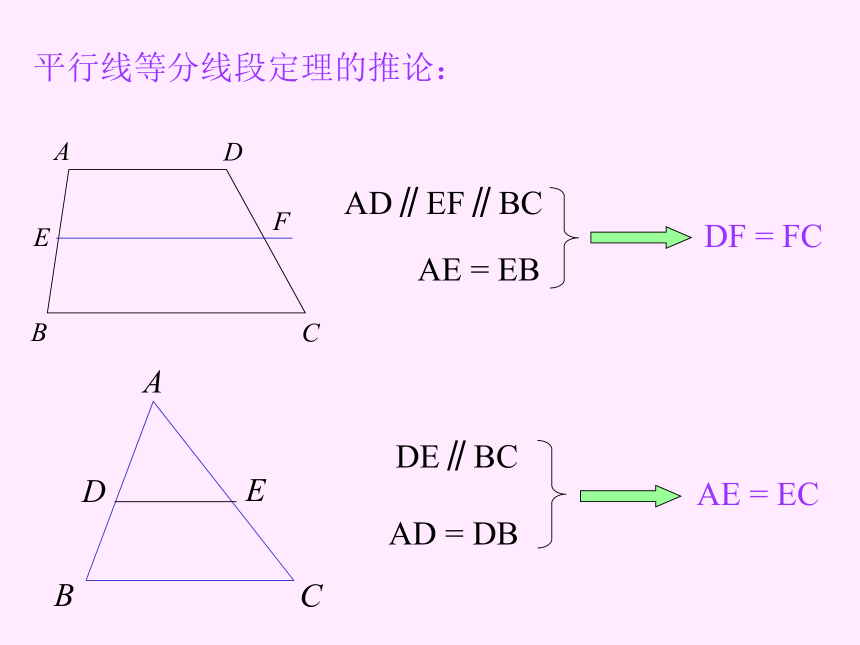
课件14张PPT。三角形和中位线平行线等分线段定理：l1∥l2∥l3∥l4∥l5∥l6∥l7AB=BC=CD=DE=EF=FGHI=IJ=JK=KL=LM=MN平行线等分线段定理的推论：AD∥EF∥BCAE = EBDF = FCDE∥BCAD = DBAE = EC三角形的中位线AD = DB
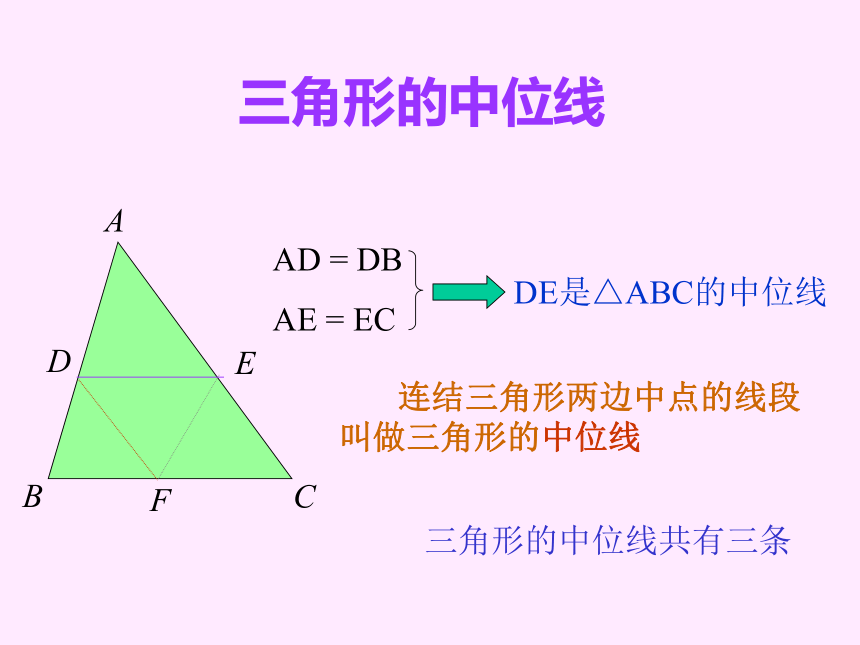
AE = ECDE是△ABC的中位线 连结三角形两边中点的线段叫做三角形的中位线三角形的中位线共有三条练习：
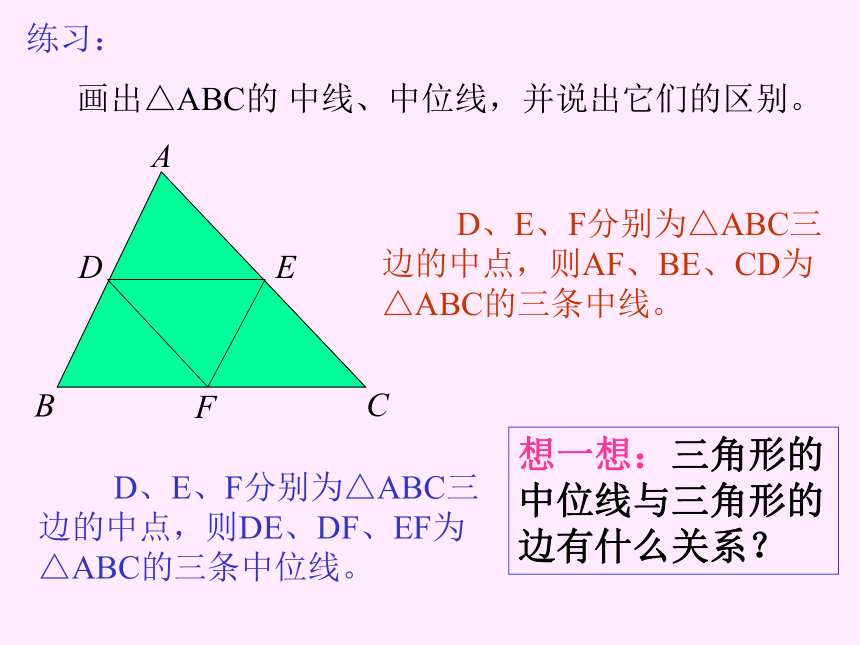
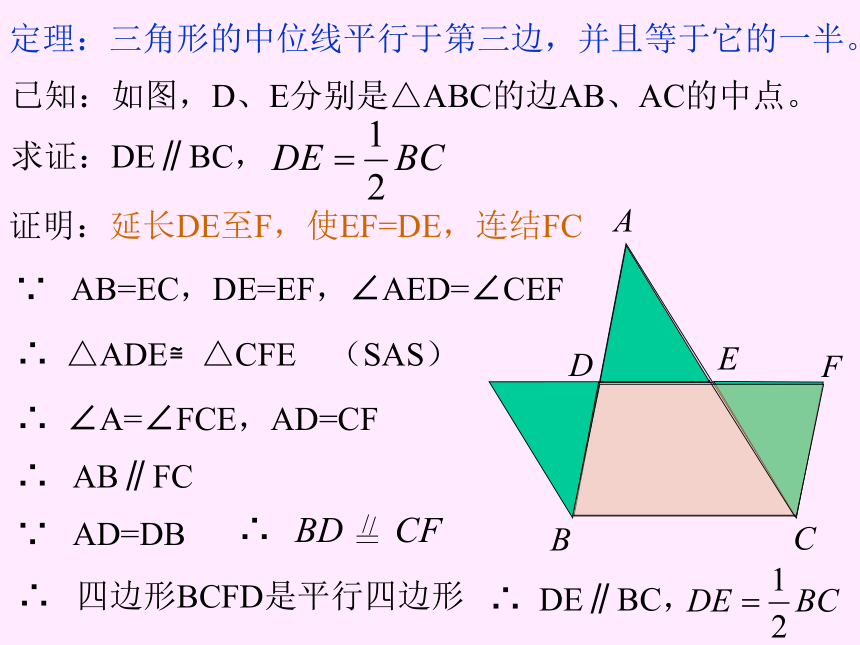
画出△ABC的 中线、中位线，并说出它们的区别。 D、E、F分别为△ABC三边的中点，则DE、DF、EF为△ABC的三条中位线。 D、E、F分别为△ABC三边的中点，则AF、BE、CD为△ABC的三条中线。想一想：三角形的中位线与三角形的边有什么关系？ 猜想：三角形的中位线平行于第三边，并且等于它 一半。如图：DE是△ABC的一条中位线。 由平行线等分线段定理推论2，得E′是AC的中点，可见DE′与DE重合，因此 DE∥BC同理，过D作DF∥AC，交BC于F，则BF=FC .∵ 四边形DFCE是平行四边形，∴ DE = FC∵∴如果过D作 ∥BC交AC于E′, 定理：三角形的中位线平行于第三边，并且等于它的一半。已知：如图，D、E分别是△ABC的边AB、AC的中点。
求证：DE∥BC，证明：延长DE至F，使EF=DE，连结FC 1.（口答） A、B两点被池塘隔开，在AB外选一点C，连结AC和BC，并分别找出AC和BC的中点M、N，如果测得MN=20 m ,那么A、B两点的距离是多少？为什么？2. 已知：三角形的各边分别为6cm 、8cm和10cm ,求连结各边中点所成三角形的周长。答案：12cm .答案：40 m .例1 求证：顺次连结四边形四条边的中点，所得的 四边形是平行四边形。证明：连结AC同理 EF∥AC，思考：平行四边形菱形矩形思考：正方形平行四边形菱形思考：菱形矩形正方形已知 ：梯形ABCD中，AD∥BC，对角线AC、BD相交于点O， 分别是AO、BO、CO、DO的中点。证明：∵ 分别是AO、BO、CO、DO的中点。 ∥小结： 连结三角形两边中点的线段叫做三角形的中位线三角形中位线定理： 三角形的中位线平行于第三边，并且等于它的一半。三角形的中位线与中线的区别。
中位线：中点与中点的连线。
中 线：顶点与中点的连线。