山西省朔州市平鲁区李林中学高中数学(人教版)必修二学案:空间两直线的位置关系(无答案)
文档属性
| 名称 | 山西省朔州市平鲁区李林中学高中数学(人教版)必修二学案:空间两直线的位置关系(无答案) | 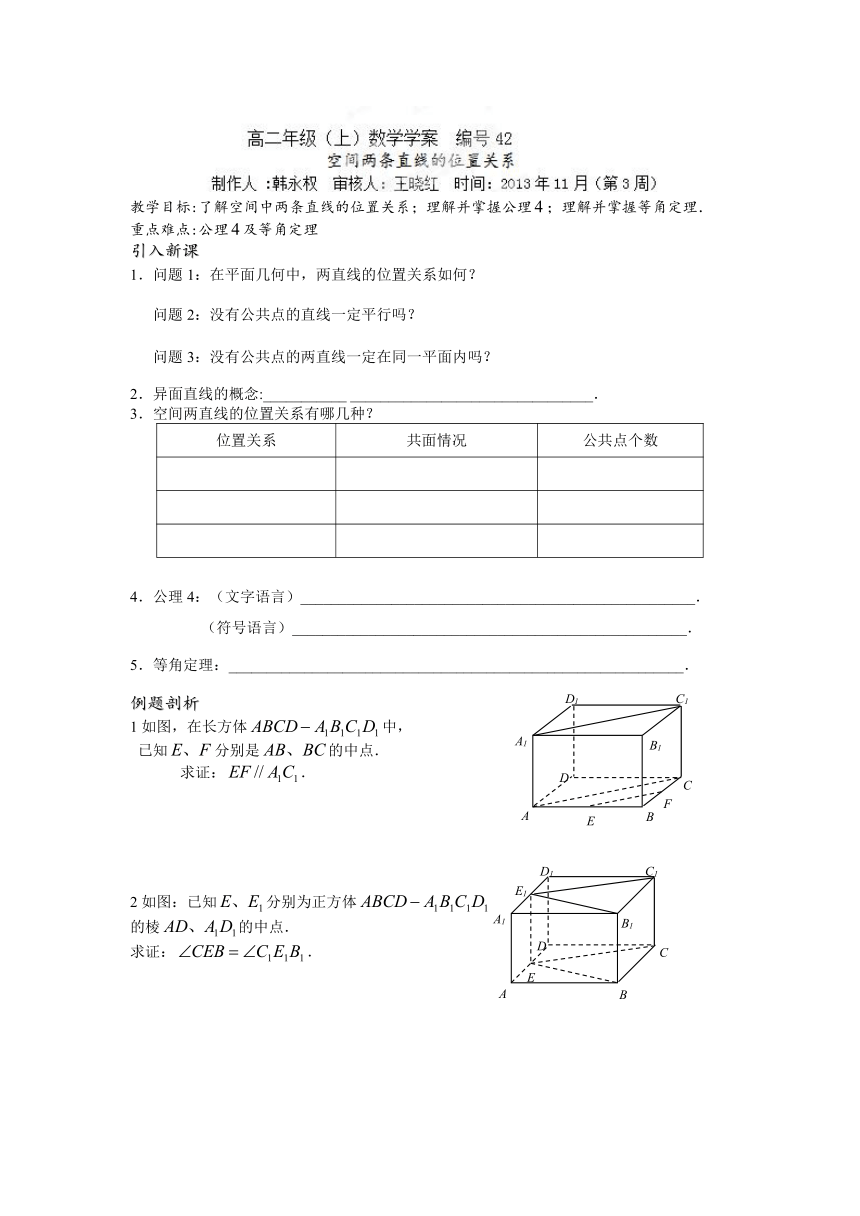 | |
| 格式 | zip | ||
| 文件大小 | 58.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-09-07 06:34:42 | ||
图片预览

文档简介
( http: / / www.21cnjy.com )
教学目标:了解空间中两条直线的位置关系;理解并掌握公理;理解并掌握等角定理.
重点难点:公理及等角定理
引入新课
1.问题1:在平面几何中,两直线的位置关系如何?
问题2:没有公共点的直线一定平行吗?
问题3:没有公共点的两直线一定在同一平面内吗?
2.异面直线的概念:___________ ________________________________.
3.空间两直线的位置关系有哪几种?
位置关系 共面情况 公共点个数
4.公理4:(文字语言)____________________________________________________.
(符号语言)____________________________________________________.
5.等角定理:____________________________________________________________.
例题剖析
1如图,在长方体中,
已知分别是的中点.
求证:.
2如图:已知分别为正方体
的棱的中点.
求证:.
( http: / / www.21cnjy.com )
巩固练习1.设是正方体的一条棱,这个正方体中与平行的棱共有( )条.
A. B. C. D.
2.是所在平面外一点,分别是和的重心,若,
则=____________________.
3.空间三条直线,若,则由直线 确定________个平面.
4.已知不共面,且,
,,.
求证:≌.
4.三棱锥中,
分别是的中点.
(1)求证:四边形是平行四边形;
(2)若,求证:四边形是菱形;
(3)当与满足什么条件时,
四边形是正方形.
A
B
E
F
C
D
A1
D1
C1
B1
A
B
C
E
D
A1
D1
E1
C1
B1
教学目标:了解空间中两条直线的位置关系;理解并掌握公理;理解并掌握等角定理.
重点难点:公理及等角定理
引入新课
1.问题1:在平面几何中,两直线的位置关系如何?
问题2:没有公共点的直线一定平行吗?
问题3:没有公共点的两直线一定在同一平面内吗?
2.异面直线的概念:___________ ________________________________.
3.空间两直线的位置关系有哪几种?
位置关系 共面情况 公共点个数
4.公理4:(文字语言)____________________________________________________.
(符号语言)____________________________________________________.
5.等角定理:____________________________________________________________.
例题剖析
1如图,在长方体中,
已知分别是的中点.
求证:.
2如图:已知分别为正方体
的棱的中点.
求证:.
( http: / / www.21cnjy.com )
巩固练习1.设是正方体的一条棱,这个正方体中与平行的棱共有( )条.
A. B. C. D.
2.是所在平面外一点,分别是和的重心,若,
则=____________________.
3.空间三条直线,若,则由直线 确定________个平面.
4.已知不共面,且,
,,.
求证:≌.
4.三棱锥中,
分别是的中点.
(1)求证:四边形是平行四边形;
(2)若,求证:四边形是菱形;
(3)当与满足什么条件时,
四边形是正方形.
A
B
E
F
C
D
A1
D1
C1
B1
A
B
C
E
D
A1
D1
E1
C1
B1
