总复习 教学课件 数学 北师大版 五年级下册(共20张PPT)
文档属性
| 名称 | 总复习 教学课件 数学 北师大版 五年级下册(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 193.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-05 09:38:14 | ||
图片预览





文档简介
(共20张PPT)
总复习
一、复习回顾
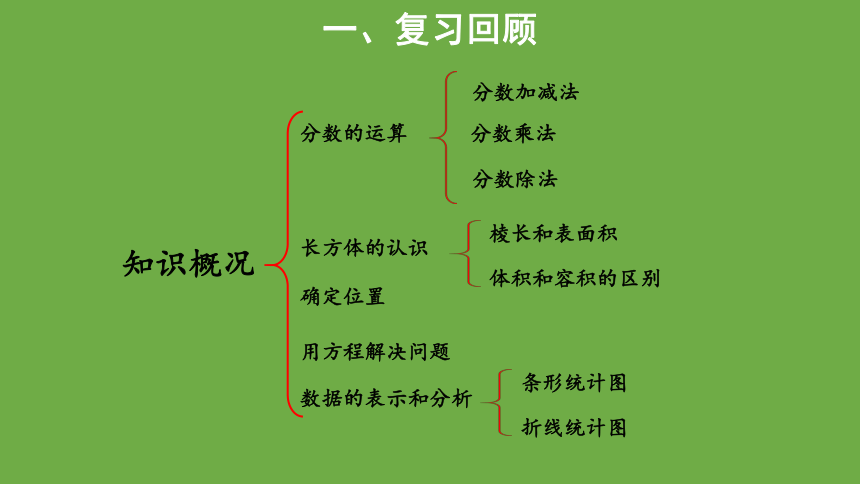
知识概况
分数的运算
确定位置
长方体的认识
用方程解决问题
数据的表示和分析
分数乘法
分数加减法
分数除法
棱长和表面积
体积和容积的区别
折线统计图
条形统计图
分数加减法
异分母分数加减法
分数加减混合运算
分数与小数的互化
分数加减法的意义
异分母分数加减法计算方法
分数加减混合运算的顺序
分数加减混合运算的简算
小数
分数
分子÷分母
先用分数表示再约分
一、复习回顾
分数乘法
分数乘整数
整数乘分数
分数乘分数
倒数
意义:求几个几分之几的和
计算方法:用分数的分子和整数相乘的积作分子,分母不变,能约分的可以先约分,再计算。
意义:求一个数的几分之几是多少
计算方法:与分数乘整数的计算方法相同
意义:求一个数的几分之几是多少
计算方法:分子相乘的积作分子,分母相乘的积作分母;能约分的可以先约分,再计算。
定义:乘积为1的两个数互为倒数
求一个倒数的方法:把这个数的分子和分母交换位置,整数可以看成分母是1的分数
一、复习回顾
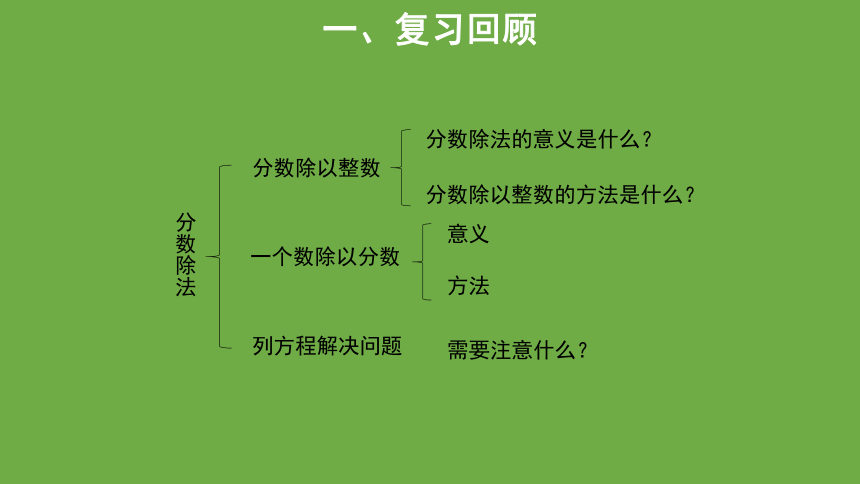
分数除法
分数除以整数
一个数除以分数
列方程解决问题
分数除法的意义是什么?
分数除以整数的方法是什么?
意义
需要注意什么?
方法
一、复习回顾
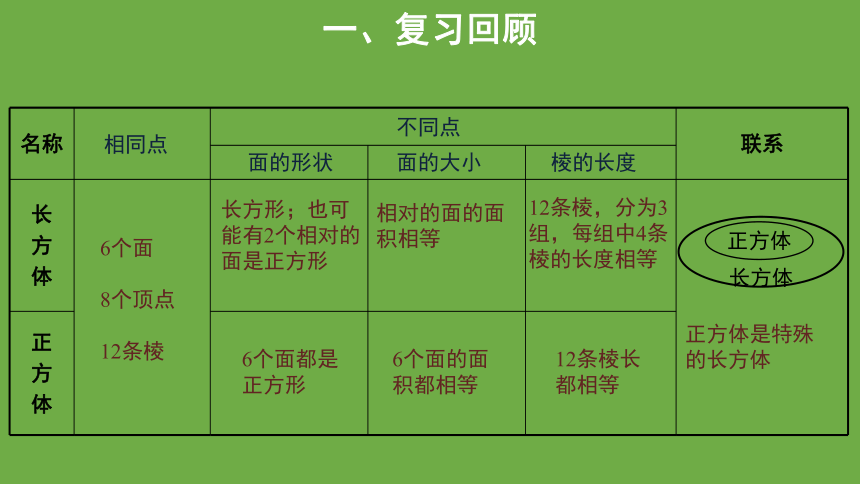
名称 联系
长 方 体
正 方 体 6个面
8个顶点
12条棱
相同点
不同点
面的形状
面的大小
棱的长度
长方体
正方体
正方体是特殊的长方体
长方形;也可能有2个相对的面是正方形
相对的面的面积相等
12条棱,分为3组,每组中4条棱的长度相等
6个面都是正方形
6个面的面积都相等
12条棱长都相等
一、复习回顾
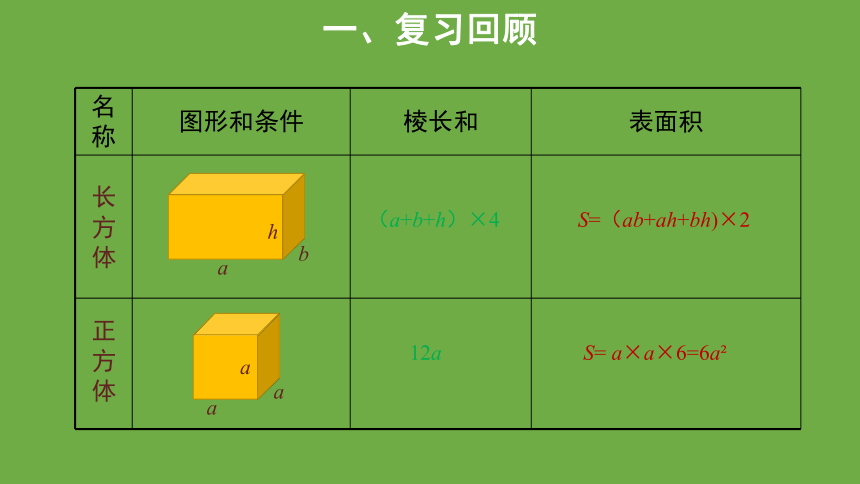
名称 图形和条件 棱长和 表面积
12a
(a+b+h)×4
S=(ab+ah+bh)×2
S= a×a×6=6a
a
a
a
a
b
h
长
方
体
正
方
体
一、复习回顾
长方体
体积与容积有什么区别?
体积单位和容积单位有哪些
长方体和正方体的体积公式是什么呢?
体积的含义
容积的含义
体积单位有哪些
容积单位有哪些
长方体的体积
正方体的体积
一、复习回顾
(1) 表示把( )平均分成( )份,取其中的( )份,它的分数单位是( ),它有( )个这样的分数单位。
6
25
单位“1”
25
6
1
25
6
(2) 千米表示把( )平均分成( )份,取其中的( )份;也表示把( )平均分成( )份,取其中的( )份。 的分数单位是( )。
1
5
3
5
1千米
5
3千米
5
1
3
5
3
二、基础练习
1.填一填。
(3)一堆货物平均分3次运完,每次运这堆
货物的( ),2次运这堆货物的( )。
(4)把4千克苹果平均分给7个小朋友,每
人分得( )千克,每人分得4千克的( )。
(5)有8朵黄花,9朵红花,黄花占总数的
( ),红花占黄花的( )。
1
3
2
3
4
7
1
7
9
8
8
17
二、基础练习
1.填一填。
2.选择题。
二、基础练习
如图,一个由8个小正方体拼成的大正方体,如果去掉一个小正方体,得到图形的表面积与原来正方体的表面积相比( )
A.无法比较 B.表面积没有变化
C.表面积变小了 D.表面积变大了
B
3.甲、乙两队合修一条公路,没修的部分占这条公路的几分之几?
甲队修了
乙队修了
1- -
= -
=
=
答:没修的部分占这条公路的 。
二、基础练习
4.一种长方体的广告灯箱,框架由铝合金条制成的,各个面由灯箱布围成。长方体的长15分米、宽10分米、高7分米。制作一个这样的广告灯箱,至少要铝合金条多少分米?
求需要铝合金条多少分米,就是求它的总棱长。
l =(a+b+h)×4
=(15+10+7)×4
=128(分米)
答:至少需要铝合金条128分米。
二、基础练习
1.花园里茶花的棵树是桂花的 。
(1)茶花有90棵,桂花有几棵?
(2)桂花有90棵,茶花有几棵?
90÷
=90×
=162(棵)
5
9
9
5
5
9
5
9
90×
=50(棵)
答:茶花有50棵。
1
18
桂花的棵树× =茶花的棵树
5
9
答:桂花有162棵。
三、易错练习
2.一个水池长2.5米,宽1.8米,深1.6米,要粉刷它的四壁及池底,粉刷的面积是多少?如果每平米花费7.8元,粉刷完一共需要多少钱?
三、易错练习
2.5×1.8+2.5×1.6×2+1.8×1.6×2=18.26(m2)
18.26×7.8=142.428(元)
答:粉刷完一共需要142.428元。
3.一个长方体玻璃容器,底面是正方形,边长是2分米,里面装有5.6升水。将一个苹果完全浸没在水中(水未溢出),这时量得容器内的水深1.5分米。这个苹果的体积是多少立方分米?
高1.5分米的水的体积是苹果的体积与原来水的体积之和。
V = abh =2×2×1.5 = 6(dm )= 6(L)
6 -5.6 = 0.4(L)= 0.4(dm )
答:苹果的体积是0.4 dm 。
三、易错练习
4.沙漏是古代的一种计时工具。一种正方体箱型沙漏的棱长是12 dm,已知平均每小时漏沙72 dm ,照这样计算,多少小时漏光一箱沙?
V正方体 = a
= 12
=1728(dm )
1728÷72=24(小时)
答:24小时漏光一箱沙。
三、易错练习
三、易错练习
5.A、B两地相距560千米,甲、乙两车从A、B两地同时出发,相向而行,经过3.5小时两车相遇。已知甲车的速度是乙车速度的 ,那么甲车、乙车的速度各是多少?
7
9
解:设乙车的速度是x千米/时,则甲车的速度是 千米/时,列方程,得
7
9
x
7
9
3.5(x+ x)=560
16
9
x=560÷3.5
16
9
x=160
x=90
答:甲车的速度是70千米/时,乙车的速度是90千米/时。
7
9
x= ×90=70(千米/时)
7
9
四、拓展练习
1.星期天妈妈用工资的 给小婷买了一台电子琴,花了1500元。后来妈妈又给小婷买了一身衣服,花去工资的 。这一天,妈妈为小婷共花了多少钱?
1
5
妈妈的工资× =买电子琴花的钱
妈妈的工资× =买衣服的钱
2
3
2
3
1
5
妈妈的工资:1500÷ =2250(元)
2
3
买衣服:2250× =450(元)
1
5
一共花了:1500+450=1950(元)
再见
总复习
一、复习回顾
知识概况
分数的运算
确定位置
长方体的认识
用方程解决问题
数据的表示和分析
分数乘法
分数加减法
分数除法
棱长和表面积
体积和容积的区别
折线统计图
条形统计图
分数加减法
异分母分数加减法
分数加减混合运算
分数与小数的互化
分数加减法的意义
异分母分数加减法计算方法
分数加减混合运算的顺序
分数加减混合运算的简算
小数
分数
分子÷分母
先用分数表示再约分
一、复习回顾
分数乘法
分数乘整数
整数乘分数
分数乘分数
倒数
意义:求几个几分之几的和
计算方法:用分数的分子和整数相乘的积作分子,分母不变,能约分的可以先约分,再计算。
意义:求一个数的几分之几是多少
计算方法:与分数乘整数的计算方法相同
意义:求一个数的几分之几是多少
计算方法:分子相乘的积作分子,分母相乘的积作分母;能约分的可以先约分,再计算。
定义:乘积为1的两个数互为倒数
求一个倒数的方法:把这个数的分子和分母交换位置,整数可以看成分母是1的分数
一、复习回顾
分数除法
分数除以整数
一个数除以分数
列方程解决问题
分数除法的意义是什么?
分数除以整数的方法是什么?
意义
需要注意什么?
方法
一、复习回顾
名称 联系
长 方 体
正 方 体 6个面
8个顶点
12条棱
相同点
不同点
面的形状
面的大小
棱的长度
长方体
正方体
正方体是特殊的长方体
长方形;也可能有2个相对的面是正方形
相对的面的面积相等
12条棱,分为3组,每组中4条棱的长度相等
6个面都是正方形
6个面的面积都相等
12条棱长都相等
一、复习回顾
名称 图形和条件 棱长和 表面积
12a
(a+b+h)×4
S=(ab+ah+bh)×2
S= a×a×6=6a
a
a
a
a
b
h
长
方
体
正
方
体
一、复习回顾
长方体
体积与容积有什么区别?
体积单位和容积单位有哪些
长方体和正方体的体积公式是什么呢?
体积的含义
容积的含义
体积单位有哪些
容积单位有哪些
长方体的体积
正方体的体积
一、复习回顾
(1) 表示把( )平均分成( )份,取其中的( )份,它的分数单位是( ),它有( )个这样的分数单位。
6
25
单位“1”
25
6
1
25
6
(2) 千米表示把( )平均分成( )份,取其中的( )份;也表示把( )平均分成( )份,取其中的( )份。 的分数单位是( )。
1
5
3
5
1千米
5
3千米
5
1
3
5
3
二、基础练习
1.填一填。
(3)一堆货物平均分3次运完,每次运这堆
货物的( ),2次运这堆货物的( )。
(4)把4千克苹果平均分给7个小朋友,每
人分得( )千克,每人分得4千克的( )。
(5)有8朵黄花,9朵红花,黄花占总数的
( ),红花占黄花的( )。
1
3
2
3
4
7
1
7
9
8
8
17
二、基础练习
1.填一填。
2.选择题。
二、基础练习
如图,一个由8个小正方体拼成的大正方体,如果去掉一个小正方体,得到图形的表面积与原来正方体的表面积相比( )
A.无法比较 B.表面积没有变化
C.表面积变小了 D.表面积变大了
B
3.甲、乙两队合修一条公路,没修的部分占这条公路的几分之几?
甲队修了
乙队修了
1- -
= -
=
=
答:没修的部分占这条公路的 。
二、基础练习
4.一种长方体的广告灯箱,框架由铝合金条制成的,各个面由灯箱布围成。长方体的长15分米、宽10分米、高7分米。制作一个这样的广告灯箱,至少要铝合金条多少分米?
求需要铝合金条多少分米,就是求它的总棱长。
l =(a+b+h)×4
=(15+10+7)×4
=128(分米)
答:至少需要铝合金条128分米。
二、基础练习
1.花园里茶花的棵树是桂花的 。
(1)茶花有90棵,桂花有几棵?
(2)桂花有90棵,茶花有几棵?
90÷
=90×
=162(棵)
5
9
9
5
5
9
5
9
90×
=50(棵)
答:茶花有50棵。
1
18
桂花的棵树× =茶花的棵树
5
9
答:桂花有162棵。
三、易错练习
2.一个水池长2.5米,宽1.8米,深1.6米,要粉刷它的四壁及池底,粉刷的面积是多少?如果每平米花费7.8元,粉刷完一共需要多少钱?
三、易错练习
2.5×1.8+2.5×1.6×2+1.8×1.6×2=18.26(m2)
18.26×7.8=142.428(元)
答:粉刷完一共需要142.428元。
3.一个长方体玻璃容器,底面是正方形,边长是2分米,里面装有5.6升水。将一个苹果完全浸没在水中(水未溢出),这时量得容器内的水深1.5分米。这个苹果的体积是多少立方分米?
高1.5分米的水的体积是苹果的体积与原来水的体积之和。
V = abh =2×2×1.5 = 6(dm )= 6(L)
6 -5.6 = 0.4(L)= 0.4(dm )
答:苹果的体积是0.4 dm 。
三、易错练习
4.沙漏是古代的一种计时工具。一种正方体箱型沙漏的棱长是12 dm,已知平均每小时漏沙72 dm ,照这样计算,多少小时漏光一箱沙?
V正方体 = a
= 12
=1728(dm )
1728÷72=24(小时)
答:24小时漏光一箱沙。
三、易错练习
三、易错练习
5.A、B两地相距560千米,甲、乙两车从A、B两地同时出发,相向而行,经过3.5小时两车相遇。已知甲车的速度是乙车速度的 ,那么甲车、乙车的速度各是多少?
7
9
解:设乙车的速度是x千米/时,则甲车的速度是 千米/时,列方程,得
7
9
x
7
9
3.5(x+ x)=560
16
9
x=560÷3.5
16
9
x=160
x=90
答:甲车的速度是70千米/时,乙车的速度是90千米/时。
7
9
x= ×90=70(千米/时)
7
9
四、拓展练习
1.星期天妈妈用工资的 给小婷买了一台电子琴,花了1500元。后来妈妈又给小婷买了一身衣服,花去工资的 。这一天,妈妈为小婷共花了多少钱?
1
5
妈妈的工资× =买电子琴花的钱
妈妈的工资× =买衣服的钱
2
3
2
3
1
5
妈妈的工资:1500÷ =2250(元)
2
3
买衣服:2250× =450(元)
1
5
一共花了:1500+450=1950(元)
再见
