青岛版数学七年级上册 7.3 第2课时 去括号、去分母解一元一次方程 课件(共18张PPT)
文档属性
| 名称 | 青岛版数学七年级上册 7.3 第2课时 去括号、去分母解一元一次方程 课件(共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 835.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-06 11:04:20 | ||
图片预览






文档简介
(共18张PPT)
第7章 一元一次方程
7.3 一元一次方程的解法
第2课时 去括号、去分母解一元一次方程
学习目标
掌握去括号解一元一次方程的方法
掌握去分母解一元一次方程的方法
掌握解一元一次方程的步骤并能灵活运用
会根据实际问题中数量关系列方程解决问题
探究解一元一次方程
如图,小红将一个正方形纸片剪去一个宽为4cm的长条后,再从剩下的长方形纸片上减去一个宽为5cm的长条,且剪下的两个长条的面积相等.问这个正方形的边长应为多少厘米?
4cm
5cm
解:
4x=5(x-4)
设正方形边长为xcm,则可列方程
对于带括号的方程,我们该如何解呢?
探究解一元一次方程
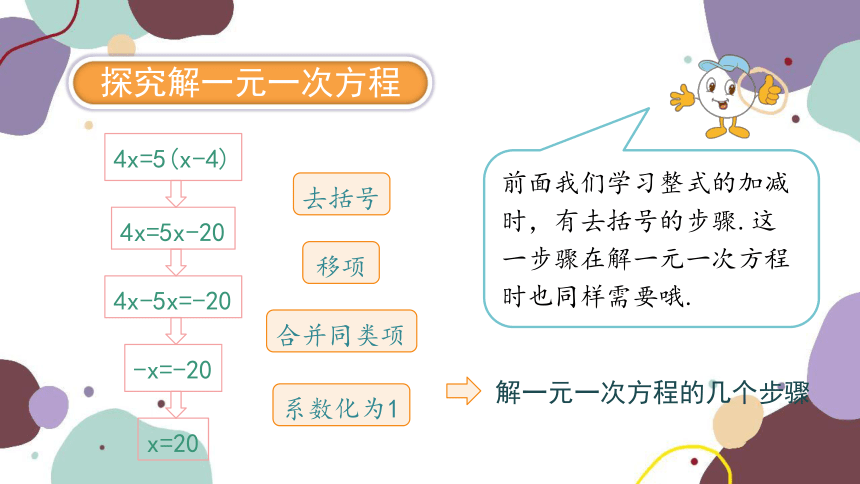
4x=5(x-4)
前面我们学习整式的加减时,有去括号的步骤.这一步骤在解一元一次方程时也同样需要哦.
4x=5x-20
去括号
4x-5x=-20
移项
-x=-20
合并同类项
x=20
系数化为1
解一元一次方程的几个步骤
解一元一次方程
像前面一样,把方程中的括号去掉,再与移项、合并同类项、系数化为1等变形相结合,最终将一元一次方程转化为x=c(c为常数)的形式,是当方程中有括号时的解方程步骤.
随堂练习
例3 解方程3(x+6)=9-5(1-2x)
解:
x=2
系数化为1,得
-7x=-14
合并同类项,得
3x-10x=9-5-18
移项,得
3x+18=9-5+10x
去括号,得
二是括号前面的数字因数,去括号时要和括号内的每一项都相乘,不要漏乘.
一是括号前面的符号,它决定了括号内各项的符号是否改变;
在解一元一次方程时,去括号应注意两点:
一辆客车和一辆卡车同时从A地出发沿同一公路同方向行驶,客车的行驶速度是70千米/小时,卡车的行驶速度是60千米/小时,客车比卡车早1小时经过B地.A,B两地间的路程是多少?
解:设A,B两地间的路程为x千米,
探究解一元一次方程
你会解这种有分母的方程吗?
像这种有分母的方程,我们一般要先去分母,去分母的步骤如下:
1.确定各分母的最小公倍数
2.方程两边同乘这个最小公倍数,约去分母
7x-6x=420
x=420
去分母
合并同类项
解一元一次方程
随堂练习
x=12
解:
去分母(方程两边都乘6),得
2x+3(20-x)=48
去括号,得
2x+60-3x=48
2x-3x=48-60
移项,得
合并同类项,得
-x=-12
系数化为1,得
去分母时,不含分母的项也要乘各分母的最小公倍数,不要漏乘.
注意!
随堂练习
解:
系数化为1,得
-6x=5
合并同类项,得
4x-10x=6-2+1
移项,得
4x+2-10x-1=6
去括号,得
2(2x+1)-(10x+1)=6
去分母,得
去分母时,要注意分数线的括号作用,当分子是多项式时,去掉分母后,原来的分子要加上括号.
注意!
解一元一次方程
通过前面的讲述,我们知道解一元一次方程时,目标是把原方程化为x=c的形式,一般步骤为:
(1)去分母
(5)未知数的系数化为1
(4)合并同类项
(3)移项
(2)去括号
解一元一次方程的步骤不是一成不变的,有的步骤可能会省略或重复,要根据方程特点灵活地选用.
随堂练习
分析:求出第一个方程的解,把该解代入第二个方程求n即可.
解:
系数化为1,得n=14
移项、合并同类项,得2n=28
去括号,得3n-1=27+3n-2n
得3n-1=3(9+n)-2n
把x=9代入3n-1=3(x+n)-2n中
系数化为1,得x=9
移项、合并同类项,得-4x=-36
去括号,得6x-9=10x-45
去分母,得3(2x-3)=5×2x-45
同解问题有法可依
两个方程同解问题解题思路有两种:
如果两个方程都含有参数,那么我们将参数看成已知数,分别解出这两个方程,然后根据两个解相等,列出一个关于参数的方程,从而求出参数的值.
如果两个方程中只有一个方程含有参数,那么我们先求出不含参数的方程的解,再将方程的解代入另一个方程得到关于参数的方程,从而求出参数的值;
总结
二是括号前面的数字因数,不要漏乘
一是括号前面的符号
去括号应注意两点:
去分母的步骤:
1.确定各分母的最小公倍数
2.方程两边同乘这个最小公倍数,约去分母
解一元一次方程一般步骤为:
(1)去分母
(5)未知数的系数化为1
(4)合并同类项
(3)移项
(2)去括号
1.去分母时,不含分母的项也要乘各分母的最小公倍数,不要漏乘.
2.去分母时,要注意分数线的括号作用,当分子是多项式时,去掉分母后,原来的分子要加上括号.
去分母应注意两点:
总结
巩固练习
B
巩固练习
D
巩固练习
解:
系数化为1,得x=0
合并同类项,得6x=0
移项,得2x+x+3x=12-12-2+2
去括号,得2x+2+x-2=12-3x-12
去分母,得2(x+1)+(x-2)=3(4-x)-12
第7章 一元一次方程
7.3 一元一次方程的解法
第2课时 去括号、去分母解一元一次方程
学习目标
掌握去括号解一元一次方程的方法
掌握去分母解一元一次方程的方法
掌握解一元一次方程的步骤并能灵活运用
会根据实际问题中数量关系列方程解决问题
探究解一元一次方程
如图,小红将一个正方形纸片剪去一个宽为4cm的长条后,再从剩下的长方形纸片上减去一个宽为5cm的长条,且剪下的两个长条的面积相等.问这个正方形的边长应为多少厘米?
4cm
5cm
解:
4x=5(x-4)
设正方形边长为xcm,则可列方程
对于带括号的方程,我们该如何解呢?
探究解一元一次方程
4x=5(x-4)
前面我们学习整式的加减时,有去括号的步骤.这一步骤在解一元一次方程时也同样需要哦.
4x=5x-20
去括号
4x-5x=-20
移项
-x=-20
合并同类项
x=20
系数化为1
解一元一次方程的几个步骤
解一元一次方程
像前面一样,把方程中的括号去掉,再与移项、合并同类项、系数化为1等变形相结合,最终将一元一次方程转化为x=c(c为常数)的形式,是当方程中有括号时的解方程步骤.
随堂练习
例3 解方程3(x+6)=9-5(1-2x)
解:
x=2
系数化为1,得
-7x=-14
合并同类项,得
3x-10x=9-5-18
移项,得
3x+18=9-5+10x
去括号,得
二是括号前面的数字因数,去括号时要和括号内的每一项都相乘,不要漏乘.
一是括号前面的符号,它决定了括号内各项的符号是否改变;
在解一元一次方程时,去括号应注意两点:
一辆客车和一辆卡车同时从A地出发沿同一公路同方向行驶,客车的行驶速度是70千米/小时,卡车的行驶速度是60千米/小时,客车比卡车早1小时经过B地.A,B两地间的路程是多少?
解:设A,B两地间的路程为x千米,
探究解一元一次方程
你会解这种有分母的方程吗?
像这种有分母的方程,我们一般要先去分母,去分母的步骤如下:
1.确定各分母的最小公倍数
2.方程两边同乘这个最小公倍数,约去分母
7x-6x=420
x=420
去分母
合并同类项
解一元一次方程
随堂练习
x=12
解:
去分母(方程两边都乘6),得
2x+3(20-x)=48
去括号,得
2x+60-3x=48
2x-3x=48-60
移项,得
合并同类项,得
-x=-12
系数化为1,得
去分母时,不含分母的项也要乘各分母的最小公倍数,不要漏乘.
注意!
随堂练习
解:
系数化为1,得
-6x=5
合并同类项,得
4x-10x=6-2+1
移项,得
4x+2-10x-1=6
去括号,得
2(2x+1)-(10x+1)=6
去分母,得
去分母时,要注意分数线的括号作用,当分子是多项式时,去掉分母后,原来的分子要加上括号.
注意!
解一元一次方程
通过前面的讲述,我们知道解一元一次方程时,目标是把原方程化为x=c的形式,一般步骤为:
(1)去分母
(5)未知数的系数化为1
(4)合并同类项
(3)移项
(2)去括号
解一元一次方程的步骤不是一成不变的,有的步骤可能会省略或重复,要根据方程特点灵活地选用.
随堂练习
分析:求出第一个方程的解,把该解代入第二个方程求n即可.
解:
系数化为1,得n=14
移项、合并同类项,得2n=28
去括号,得3n-1=27+3n-2n
得3n-1=3(9+n)-2n
把x=9代入3n-1=3(x+n)-2n中
系数化为1,得x=9
移项、合并同类项,得-4x=-36
去括号,得6x-9=10x-45
去分母,得3(2x-3)=5×2x-45
同解问题有法可依
两个方程同解问题解题思路有两种:
如果两个方程都含有参数,那么我们将参数看成已知数,分别解出这两个方程,然后根据两个解相等,列出一个关于参数的方程,从而求出参数的值.
如果两个方程中只有一个方程含有参数,那么我们先求出不含参数的方程的解,再将方程的解代入另一个方程得到关于参数的方程,从而求出参数的值;
总结
二是括号前面的数字因数,不要漏乘
一是括号前面的符号
去括号应注意两点:
去分母的步骤:
1.确定各分母的最小公倍数
2.方程两边同乘这个最小公倍数,约去分母
解一元一次方程一般步骤为:
(1)去分母
(5)未知数的系数化为1
(4)合并同类项
(3)移项
(2)去括号
1.去分母时,不含分母的项也要乘各分母的最小公倍数,不要漏乘.
2.去分母时,要注意分数线的括号作用,当分子是多项式时,去掉分母后,原来的分子要加上括号.
去分母应注意两点:
总结
巩固练习
B
巩固练习
D
巩固练习
解:
系数化为1,得x=0
合并同类项,得6x=0
移项,得2x+x+3x=12-12-2+2
去括号,得2x+2+x-2=12-3x-12
去分母,得2(x+1)+(x-2)=3(4-x)-12
同课章节目录
- 第1章 基本的几何图形
- 1.1 我们身边的图形世界
- 1.2 几何图形
- 1.3 线段、射线和直线
- 1.4 线段的比较与作法
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数与绝对值
- 第3章 有理数的运算
- 3.1 有理数的加法与减法
- 3.2 有理数的乘法与除法
- 3.3 有理数的乘方
- 3.4 有理数的混合运算
- 3.5 利用计算器进行有理数的计算
- 第4章 数据的收集整理与描述
- 4.1 普查和抽样调查
- 4.2 简单随机抽样
- 4.3 数据的整理
- 4.4 扇形统计图
- 第5章 代数式与函数的初步认识
- 5.1 用字母表示数
- 5.2 代数式
- 5.3 代数式的值
- 5.4 生活中的常量与变量
- 5.5 函数的初步认识
- 第6章 整式的加减
- 6.1 单项式与多项式
- 6.2 同类项
- 6.3 去括号
- 6.4 整式的加减
- 第7章 一元一次方程
- 7.1 等式的基本性质
- 7.2 一元一次方程
- 7.3 一元一次方程的解法
- 7.4 一元一次方程的应用
