5.3.1简单的轴对称图形(第1课时) 课件(共29张PPT)
文档属性
| 名称 | 5.3.1简单的轴对称图形(第1课时) 课件(共29张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-05 13:59:44 | ||
图片预览




文档简介
(共29张PPT)
新课标 北师大版
七年级下册
5.3.1简单的轴对称图形(第1课时)
第五章
生活中的轴对称
学习目标
1.经历探索简单图形的轴对称的过程,进一步理解轴对称的性质,积累数学活动经验,发展空间观念.
2.探索并了解线段的对称性及其相关性质.
轴对称
图形
两个图形
成轴对称
轴对称
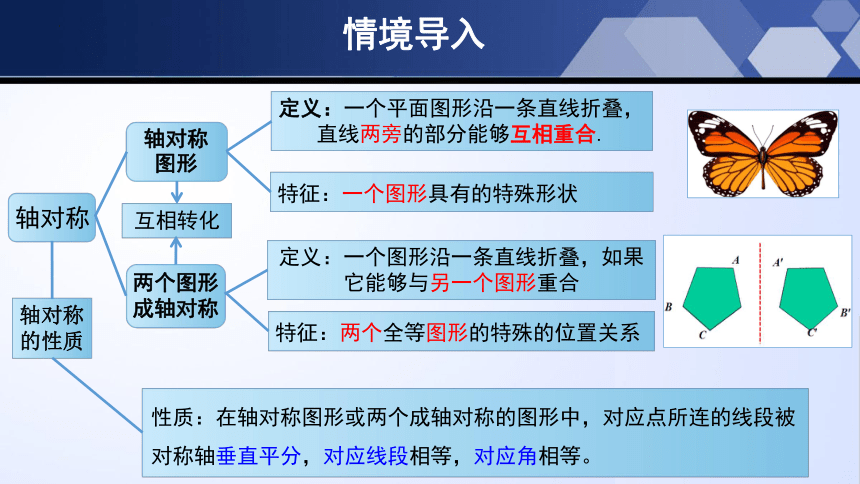
定义:一个平面图形沿一条直线折叠,直线两旁的部分能够互相重合.
定义:一个图形沿一条直线折叠,如果它能够与另一个图形重合
特征:一个图形具有的特殊形状
特征:两个全等图形的特殊的位置关系
互相转化
性质:在轴对称图形或两个成轴对称的图形中,对应点所连的线段被对称轴垂直平分,对应线段相等,对应角相等。
轴对称
的性质
情境导入
情境导入
问题:左列图片中有你熟悉的几何图形吗?
探究新知
核心知识点一:
等腰三角形的性质
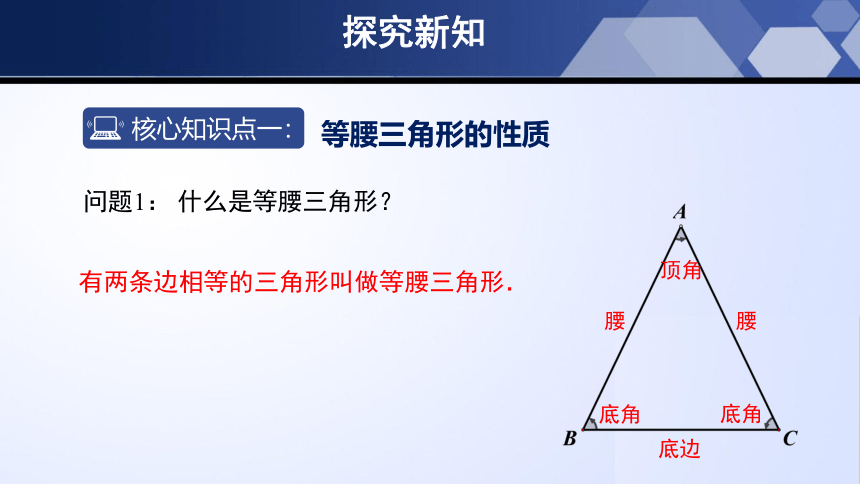
问题1: 什么是等腰三角形?
有两条边相等的三角形叫做等腰三角形.
腰
腰
底边
顶角
底角
底角
探究新知
问题2: 等腰三角形有哪些特征呢
(1)你有哪些方法可以得到一个等腰三角形?
(2)等腰三角形是轴对称图形吗?
(3)你是如何找出等腰三角形的对称轴呢?
(4)等腰三角形有几条对称轴?
(5)等腰三角形“三线合一”的性质与等腰三角形的形状有关吗?
探究新知
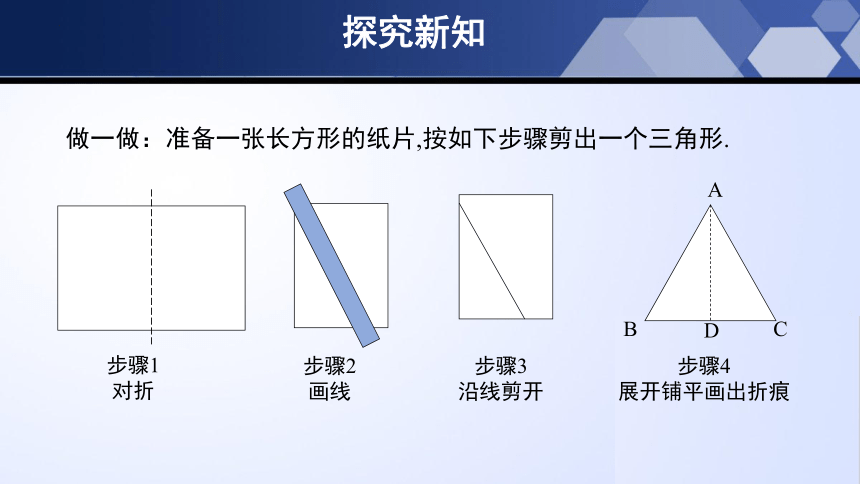
做一做:准备一张长方形的纸片,按如下步骤剪出一个三角形.
A
D
C
B
步骤1
对折
步骤2
画线
步骤3
沿线剪开
步骤4
展开铺平画出折痕
探究新知
A
B
C
AB=AC
等腰三角形
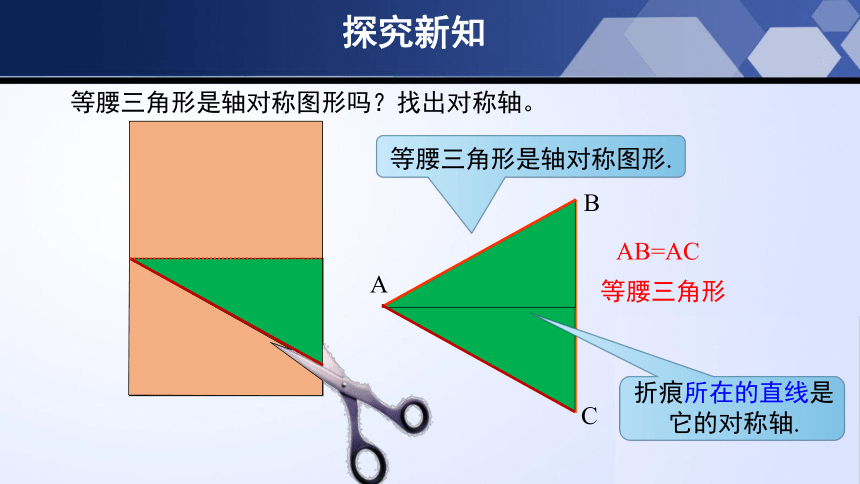
等腰三角形是轴对称图形.
折痕所在的直线是
它的对称轴.
等腰三角形是轴对称图形吗?找出对称轴。
探究新知
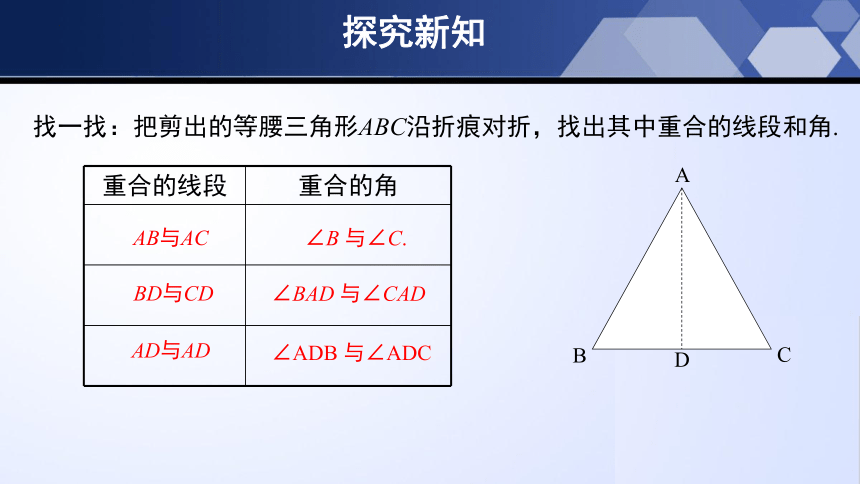
找一找:把剪出的等腰三角形ABC沿折痕对折,找出其中重合的线段和角.
重合的线段 重合的角
AB与AC
BD与CD
AD与AD
∠B 与∠C.
∠BAD 与∠CAD
∠ADB 与∠ADC
A
D
C
B
探究新知
猜一猜:由这些重合的角,你能发现等腰三角形的性质吗?说一说你的猜想.
(1)BD=CD,
AD为底边上的中线.
(2)∠BAD=∠CAD,
AD为顶角的平分线.
(3)∠ADB=∠ADC=90°
AD为底边上的高.
(4)∠B =∠C .
等腰三角形的两个底角相等.
对于1,2,3这三个结果如何表述成命题
等腰三角形底边上的中线、高及顶角角平分线互相重合。
简称“三线合一”
探究新知
已知在△ABC中,AB=AC,AD平分∠BAC.
求证:AD为底边BC上的中线,且AD为底边BC上的高.
问题3 :你能证明等腰三角形“三线合一”吗?
D
探究新知
证明:∵ AD平分∠BAC,
∴∠BAD=∠CAD.
∴△ABD≌△ACD(SSS),
∵在△ABD和△ACD中,
∴BD=CD,
∠ADB=∠ADC,
即AD为底边BC的中线,
∴BD=CD,
∠ADB=∠ADC,
即AD为底边BC的中线,
D
探究新知
归纳总结
等腰三角形顶角的平分线、底边上的中线、底边上的高重合(也称“三线合一”),它们所在的直线都是等腰三角形的对称轴.
A
B
C
D
在△ABC中,AB=AC,
∵AD⊥BC,
∴∠BAD=∠CAD,BD=CD.
在△ABC中,AB=AC,
∵∠BAD=∠CAD,
∴AD⊥BC,BD=CD.
在△ABC中,AB=AC,
∵BD=CD,
∴∠BAD=∠CAD,AD⊥BC.
知其一,得另二
探究新知
归纳总结
等腰三角形的两个底角相等.
在△ABC中,
∵AB=AC,
∴∠B=∠C.
几何语言:
A
B
C
D
简称为:“等边对等角”.
探究新知
核心知识点二:
等边三角形的性质
(1)等边三角形有几条对称轴?
等边三角形有三条对称轴.
等边三角形是特殊的等腰三角形.
一般到特殊!
探究新知
(2)你能发现它的哪些特征?
文字语言:
等边三角形的三个内角都相等,且每个内角都是60°.
几何语言:
∵△ABC是等边三角形,
∴∠A=∠B= ∠C=60°.
A
C
B
探究新知
归纳总结
等边三角形是轴对称图形,共有三条对称轴。
等边三角形每个角的平分线和这个角的对边上的中线、高线重合(简称“三线合一”),它们所在的直线都是等边三角形的对称轴。
等边三角形的各角都相等,都等于60°
A
C
B
随堂练习
1.如图,在△ABC中,AB=AC,点D为BC的中点,则下列结论中错误的是( )
A.∠BAD=∠CAD
B.AD⊥BC
C.∠B=∠C
D.∠BAC=∠B
D
随堂练习
2.如图,AD,CE分别是△ABC的中线和角平分线,若AB=AC,∠CAD=20°,则∠ACE的度数是( )
A.20° B.35°
C.40° D.70°
B
随堂练习
3. 如图,在等腰三角形ABC中,AB=AC,AD为∠BAC的平分线,AD=3,BC=4,则图中阴影部分的面积是( )
A.3 B.6
C.9 D.12
A
随堂练习
4. 如图,在等腰三角形ABC中,AB=AC,BD⊥AC,∠ABC=72°,则∠ABD等于( )
A.36° B.54°
C.18° D.64°
B
随堂练习
5. 如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A′B′C,连接AA′,若∠1=25°,则∠BAA′的度数是( )
A.55° B.60°
C.65° D.70°
C
随堂练习
6. 已知:如图,四边形ABCD中,AB=BC,AD=CD.
试说明:∠A=∠C.
随堂练习
解:如图,连接AC. 因为AB=BC,
所以∠BAC=∠BCA.
因为AD=CD,
所以∠DAC=∠DCA.
所以∠BAC+∠DAC=∠BCA+∠DCA,
即∠BAD=∠BCD.
随堂练习
7.如图,四边形ABCD是正方形,△EBC是等边三角形.
(1)试说明:△ABE≌△DCE;
(2)求∠AED的度数.
随堂练习
随堂练习
(2).由(1)可知AB=BE,∠ABE=30°,
所以∠BAE=∠BEA=75°.
同理,∠CDE=∠CED=75°.
所以∠AED=360°-75°-75°-60°=150°.
课堂小结
A
B
C
D
4.“三线合一”
1.两腰相等
3.等边对等角
2.轴对称图形
A
C
B
三个内角都相等,
且每个内角都是60°.
三条边都相等
等腰三角形
等边三角形
谢 谢 ~
新课标 北师大版
七年级下册
5.3.1简单的轴对称图形(第1课时)
第五章
生活中的轴对称
学习目标
1.经历探索简单图形的轴对称的过程,进一步理解轴对称的性质,积累数学活动经验,发展空间观念.
2.探索并了解线段的对称性及其相关性质.
轴对称
图形
两个图形
成轴对称
轴对称
定义:一个平面图形沿一条直线折叠,直线两旁的部分能够互相重合.
定义:一个图形沿一条直线折叠,如果它能够与另一个图形重合
特征:一个图形具有的特殊形状
特征:两个全等图形的特殊的位置关系
互相转化
性质:在轴对称图形或两个成轴对称的图形中,对应点所连的线段被对称轴垂直平分,对应线段相等,对应角相等。
轴对称
的性质
情境导入
情境导入
问题:左列图片中有你熟悉的几何图形吗?
探究新知
核心知识点一:
等腰三角形的性质
问题1: 什么是等腰三角形?
有两条边相等的三角形叫做等腰三角形.
腰
腰
底边
顶角
底角
底角
探究新知
问题2: 等腰三角形有哪些特征呢
(1)你有哪些方法可以得到一个等腰三角形?
(2)等腰三角形是轴对称图形吗?
(3)你是如何找出等腰三角形的对称轴呢?
(4)等腰三角形有几条对称轴?
(5)等腰三角形“三线合一”的性质与等腰三角形的形状有关吗?
探究新知
做一做:准备一张长方形的纸片,按如下步骤剪出一个三角形.
A
D
C
B
步骤1
对折
步骤2
画线
步骤3
沿线剪开
步骤4
展开铺平画出折痕
探究新知
A
B
C
AB=AC
等腰三角形
等腰三角形是轴对称图形.
折痕所在的直线是
它的对称轴.
等腰三角形是轴对称图形吗?找出对称轴。
探究新知
找一找:把剪出的等腰三角形ABC沿折痕对折,找出其中重合的线段和角.
重合的线段 重合的角
AB与AC
BD与CD
AD与AD
∠B 与∠C.
∠BAD 与∠CAD
∠ADB 与∠ADC
A
D
C
B
探究新知
猜一猜:由这些重合的角,你能发现等腰三角形的性质吗?说一说你的猜想.
(1)BD=CD,
AD为底边上的中线.
(2)∠BAD=∠CAD,
AD为顶角的平分线.
(3)∠ADB=∠ADC=90°
AD为底边上的高.
(4)∠B =∠C .
等腰三角形的两个底角相等.
对于1,2,3这三个结果如何表述成命题
等腰三角形底边上的中线、高及顶角角平分线互相重合。
简称“三线合一”
探究新知
已知在△ABC中,AB=AC,AD平分∠BAC.
求证:AD为底边BC上的中线,且AD为底边BC上的高.
问题3 :你能证明等腰三角形“三线合一”吗?
D
探究新知
证明:∵ AD平分∠BAC,
∴∠BAD=∠CAD.
∴△ABD≌△ACD(SSS),
∵在△ABD和△ACD中,
∴BD=CD,
∠ADB=∠ADC,
即AD为底边BC的中线,
∴BD=CD,
∠ADB=∠ADC,
即AD为底边BC的中线,
D
探究新知
归纳总结
等腰三角形顶角的平分线、底边上的中线、底边上的高重合(也称“三线合一”),它们所在的直线都是等腰三角形的对称轴.
A
B
C
D
在△ABC中,AB=AC,
∵AD⊥BC,
∴∠BAD=∠CAD,BD=CD.
在△ABC中,AB=AC,
∵∠BAD=∠CAD,
∴AD⊥BC,BD=CD.
在△ABC中,AB=AC,
∵BD=CD,
∴∠BAD=∠CAD,AD⊥BC.
知其一,得另二
探究新知
归纳总结
等腰三角形的两个底角相等.
在△ABC中,
∵AB=AC,
∴∠B=∠C.
几何语言:
A
B
C
D
简称为:“等边对等角”.
探究新知
核心知识点二:
等边三角形的性质
(1)等边三角形有几条对称轴?
等边三角形有三条对称轴.
等边三角形是特殊的等腰三角形.
一般到特殊!
探究新知
(2)你能发现它的哪些特征?
文字语言:
等边三角形的三个内角都相等,且每个内角都是60°.
几何语言:
∵△ABC是等边三角形,
∴∠A=∠B= ∠C=60°.
A
C
B
探究新知
归纳总结
等边三角形是轴对称图形,共有三条对称轴。
等边三角形每个角的平分线和这个角的对边上的中线、高线重合(简称“三线合一”),它们所在的直线都是等边三角形的对称轴。
等边三角形的各角都相等,都等于60°
A
C
B
随堂练习
1.如图,在△ABC中,AB=AC,点D为BC的中点,则下列结论中错误的是( )
A.∠BAD=∠CAD
B.AD⊥BC
C.∠B=∠C
D.∠BAC=∠B
D
随堂练习
2.如图,AD,CE分别是△ABC的中线和角平分线,若AB=AC,∠CAD=20°,则∠ACE的度数是( )
A.20° B.35°
C.40° D.70°
B
随堂练习
3. 如图,在等腰三角形ABC中,AB=AC,AD为∠BAC的平分线,AD=3,BC=4,则图中阴影部分的面积是( )
A.3 B.6
C.9 D.12
A
随堂练习
4. 如图,在等腰三角形ABC中,AB=AC,BD⊥AC,∠ABC=72°,则∠ABD等于( )
A.36° B.54°
C.18° D.64°
B
随堂练习
5. 如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A′B′C,连接AA′,若∠1=25°,则∠BAA′的度数是( )
A.55° B.60°
C.65° D.70°
C
随堂练习
6. 已知:如图,四边形ABCD中,AB=BC,AD=CD.
试说明:∠A=∠C.
随堂练习
解:如图,连接AC. 因为AB=BC,
所以∠BAC=∠BCA.
因为AD=CD,
所以∠DAC=∠DCA.
所以∠BAC+∠DAC=∠BCA+∠DCA,
即∠BAD=∠BCD.
随堂练习
7.如图,四边形ABCD是正方形,△EBC是等边三角形.
(1)试说明:△ABE≌△DCE;
(2)求∠AED的度数.
随堂练习
随堂练习
(2).由(1)可知AB=BE,∠ABE=30°,
所以∠BAE=∠BEA=75°.
同理,∠CDE=∠CED=75°.
所以∠AED=360°-75°-75°-60°=150°.
课堂小结
A
B
C
D
4.“三线合一”
1.两腰相等
3.等边对等角
2.轴对称图形
A
C
B
三个内角都相等,
且每个内角都是60°.
三条边都相等
等腰三角形
等边三角形
谢 谢 ~
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
