5.1轴对称现象 课件(共25张PPT)
文档属性
| 名称 | 5.1轴对称现象 课件(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-05 14:52:49 | ||
图片预览








文档简介
新课标 北师大版
七年级下册
5.1轴对称现象
第五章
生活中的轴对称
学习目标
1.在生活实例中认识轴对称图形;
2.分析轴对称图形,理解轴对称的概念;
3.通过丰富的生活实例认识轴对称,能够识别简
单的轴对称图形及其对称轴.
情境导入
想一想:这些图片有什么共同的特征吗?
情境导入
无论是艺术家的创造,还是日常生活中图案的设计,都有对称的身影。初步掌握对称的奥妙,不仅可以帮助我们发现一些图形的特征,还可以使我们感受到自然界的美与和谐,并能够根据自己的设想创造出对称的作品,装点生活。
本章,我们将认识生活中的轴对称现象,探索轴对称的奥妙并利用它解决问题。
探究新知
核心知识点一:
轴对称和轴对称图形
请你想一想:将上图中的每一个图形沿某条直线对折,直线两旁的部分能完全重合吗?
我们能不能给具有这样特征的一个图形起一个名称呢?
探究新知
归纳总结
定义:如果一个平面图形沿一条直线折叠后,直线两旁的部分能够互相重合,那么这个图形叫做轴对称图形,这条直线叫做对称轴.
用于判断一个图形是否为轴对称图形。
对称轴是一条直线,不是线段也不是射线!
探究新知
练一练:1.如图的标志中,可以看作是轴对称图形的是( )
D
探究新知
2.如图,判断下列图形是否为轴对称图形.如果是,画出对称轴.
探究新知
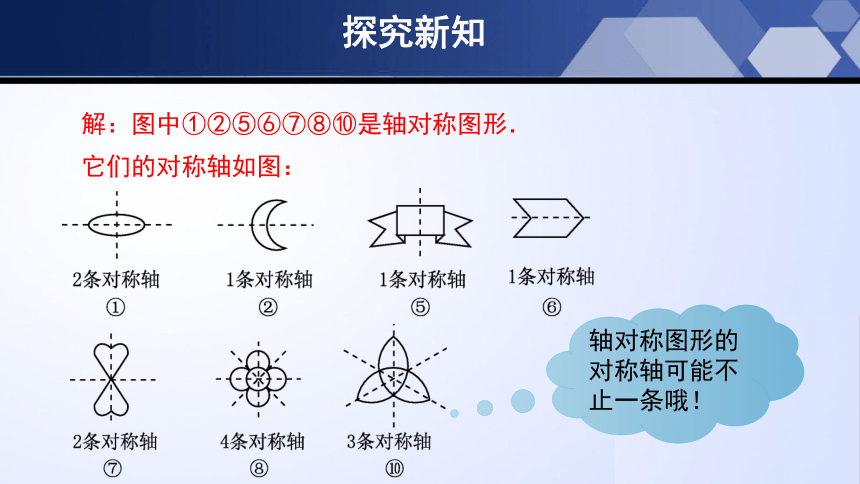
解:图中①②⑤⑥⑦⑧⑩是轴对称图形.
它们的对称轴如图:
轴对称图形的对称轴可能不止一条哦!
探究新知
思考:观察下面的每组图案,你发现了什么?
探究新知
定义: 如果两个平面图形沿一条直线折叠后能够完全重合,那么称这两个图形成轴对称,这条直线叫做这两个图形的对称轴.折叠后重合的点是对应点,叫做对称点.
两层含义:
(1)有两个图形,且形状、大小完全相同.
(2)两个图形的位置必须满足沿一条直线对折后能完全重合.
归纳总结
探究新知
练一练:分别观察图中的①~⑤中的两个图形,它们是轴对称的吗?有什么共同特点?
解:它们都是轴对称的,每一组中都有两个图形,都可以沿某一条直线对折使两个图形完全重合在一起,所以每组图中的两个图形成轴对称.
探究新知
归纳总结
联系:
区别:
都是沿一条直线折叠后能够互相重合。
轴对称图形是一个图形。轴对称是两个图形之间的关系。
轴对称图形
轴对称
轴对称图形和轴对称的关系:
探究新知
请你举出生活中的轴对称和轴对称图形?
轴对称图形:
圆、正方形、长方形、菱形、等腰三角形、等边三角形、等腰梯形、线段、角……
注意:平行四边形不是轴对称图形
轴对称:
两扇大门、一双鞋、两只手、同一人的两脸颊、物体和镜中的像……
探究新知
生活中常见的轴对称
脸谱艺术
探究新知
国旗设计
摩洛哥
瑞典
约旦
也门
英国
肯尼亚
生活中常见的轴对称
随堂练习
一、选择题。
1.下面四个手机的图标中,是轴对称图形的是 ( )
2.如图所示图形是轴对称图形,其对称轴共有( )
A.1条 B.2条
C.4条 D.无数条
A
C
随堂练习
3.在这四个文字中,不是轴对称图形的是 ( )
4.下列四个图形中,不是轴对称图形的是 ( )
D
A
随堂练习
二、填空题。
1.下面四个中文艺术字中,不是轴对称图形的是 字.?
2.如图所示的各组图形中,左边的图形与右边的图形关于某条直线成轴对称的是 .(填序号)?
千
①③
随堂练习
三、解答题。
1.下面的图形是轴对称图形吗?如果是,请画出它的对称轴.(画出所有你想到的对称轴)
随堂练习
2.如图所示,依据你的观察填表.
(1)填表:
几何图形
正三角形
正方形
正五边形
正六边形
……
对称轴条数
…
(2)根据你发现的规律说出正100边形、正n边形的对称轴的条数.
3
4
5
6
解:正100边形有100条对称轴,正n边形有n条对称轴.
随堂练习
3.如图是4×4正方形网格,其中已有3个小方格涂成了黑色.现在要从其余13个白色小方格中选出一个也涂成黑色,使整个涂成黑色的图形成为轴对称图形,这样的白色小方格有几个?
解:如图所示,有4个位置使之成为轴对称图形.故这样的白色小方格有4个.
?
随堂练习
4. 如图,有阴影的三角形与哪些三角形成轴对称?整个图形是轴对称图形吗?它共有几条对称轴?
解:图中有阴影的三角形与三角形1,3成轴对称;
整个图形是轴对称图形;
它共有2条对称轴.
课堂小结
1、轴对称图形和两个图形成轴对称的定义及判别方法;
2、轴对称图形和两个图形成轴对称的区别与联系;
3、对称轴是一条直线;
4、一个轴对称图形的对称轴可能有多条,而两个图形成轴对称的对称轴一般只有一条.
谢 谢 ~
七年级下册
5.1轴对称现象
第五章
生活中的轴对称
学习目标
1.在生活实例中认识轴对称图形;
2.分析轴对称图形,理解轴对称的概念;
3.通过丰富的生活实例认识轴对称,能够识别简
单的轴对称图形及其对称轴.
情境导入
想一想:这些图片有什么共同的特征吗?
情境导入
无论是艺术家的创造,还是日常生活中图案的设计,都有对称的身影。初步掌握对称的奥妙,不仅可以帮助我们发现一些图形的特征,还可以使我们感受到自然界的美与和谐,并能够根据自己的设想创造出对称的作品,装点生活。
本章,我们将认识生活中的轴对称现象,探索轴对称的奥妙并利用它解决问题。
探究新知
核心知识点一:
轴对称和轴对称图形
请你想一想:将上图中的每一个图形沿某条直线对折,直线两旁的部分能完全重合吗?
我们能不能给具有这样特征的一个图形起一个名称呢?
探究新知
归纳总结
定义:如果一个平面图形沿一条直线折叠后,直线两旁的部分能够互相重合,那么这个图形叫做轴对称图形,这条直线叫做对称轴.
用于判断一个图形是否为轴对称图形。
对称轴是一条直线,不是线段也不是射线!
探究新知
练一练:1.如图的标志中,可以看作是轴对称图形的是( )
D
探究新知
2.如图,判断下列图形是否为轴对称图形.如果是,画出对称轴.
探究新知
解:图中①②⑤⑥⑦⑧⑩是轴对称图形.
它们的对称轴如图:
轴对称图形的对称轴可能不止一条哦!
探究新知
思考:观察下面的每组图案,你发现了什么?
探究新知
定义: 如果两个平面图形沿一条直线折叠后能够完全重合,那么称这两个图形成轴对称,这条直线叫做这两个图形的对称轴.折叠后重合的点是对应点,叫做对称点.
两层含义:
(1)有两个图形,且形状、大小完全相同.
(2)两个图形的位置必须满足沿一条直线对折后能完全重合.
归纳总结
探究新知
练一练:分别观察图中的①~⑤中的两个图形,它们是轴对称的吗?有什么共同特点?
解:它们都是轴对称的,每一组中都有两个图形,都可以沿某一条直线对折使两个图形完全重合在一起,所以每组图中的两个图形成轴对称.
探究新知
归纳总结
联系:
区别:
都是沿一条直线折叠后能够互相重合。
轴对称图形是一个图形。轴对称是两个图形之间的关系。
轴对称图形
轴对称
轴对称图形和轴对称的关系:
探究新知
请你举出生活中的轴对称和轴对称图形?
轴对称图形:
圆、正方形、长方形、菱形、等腰三角形、等边三角形、等腰梯形、线段、角……
注意:平行四边形不是轴对称图形
轴对称:
两扇大门、一双鞋、两只手、同一人的两脸颊、物体和镜中的像……
探究新知
生活中常见的轴对称
脸谱艺术
探究新知
国旗设计
摩洛哥
瑞典
约旦
也门
英国
肯尼亚
生活中常见的轴对称
随堂练习
一、选择题。
1.下面四个手机的图标中,是轴对称图形的是 ( )
2.如图所示图形是轴对称图形,其对称轴共有( )
A.1条 B.2条
C.4条 D.无数条
A
C
随堂练习
3.在这四个文字中,不是轴对称图形的是 ( )
4.下列四个图形中,不是轴对称图形的是 ( )
D
A
随堂练习
二、填空题。
1.下面四个中文艺术字中,不是轴对称图形的是 字.?
2.如图所示的各组图形中,左边的图形与右边的图形关于某条直线成轴对称的是 .(填序号)?
千
①③
随堂练习
三、解答题。
1.下面的图形是轴对称图形吗?如果是,请画出它的对称轴.(画出所有你想到的对称轴)
随堂练习
2.如图所示,依据你的观察填表.
(1)填表:
几何图形
正三角形
正方形
正五边形
正六边形
……
对称轴条数
…
(2)根据你发现的规律说出正100边形、正n边形的对称轴的条数.
3
4
5
6
解:正100边形有100条对称轴,正n边形有n条对称轴.
随堂练习
3.如图是4×4正方形网格,其中已有3个小方格涂成了黑色.现在要从其余13个白色小方格中选出一个也涂成黑色,使整个涂成黑色的图形成为轴对称图形,这样的白色小方格有几个?
解:如图所示,有4个位置使之成为轴对称图形.故这样的白色小方格有4个.
?
随堂练习
4. 如图,有阴影的三角形与哪些三角形成轴对称?整个图形是轴对称图形吗?它共有几条对称轴?
解:图中有阴影的三角形与三角形1,3成轴对称;
整个图形是轴对称图形;
它共有2条对称轴.
课堂小结
1、轴对称图形和两个图形成轴对称的定义及判别方法;
2、轴对称图形和两个图形成轴对称的区别与联系;
3、对称轴是一条直线;
4、一个轴对称图形的对称轴可能有多条,而两个图形成轴对称的对称轴一般只有一条.
谢 谢 ~
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
