2.3简谐运动的回复力和能量 课件 (共21张PPT)
文档属性
| 名称 | 2.3简谐运动的回复力和能量 课件 (共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-06-05 15:09:56 | ||
图片预览

文档简介
(共21张PPT)
第二章 机械振动
2.3 简谐运动的回复力和能量
restoring force and energy
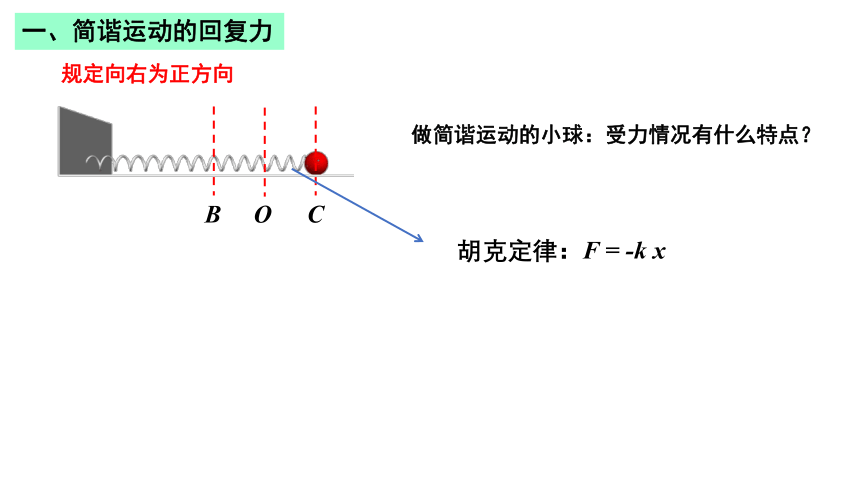
做简谐运动的小球:受力情况有什么特点?
一、简谐运动的回复力
C
B
O
规定向右为正方向
胡克定律:F = -k x
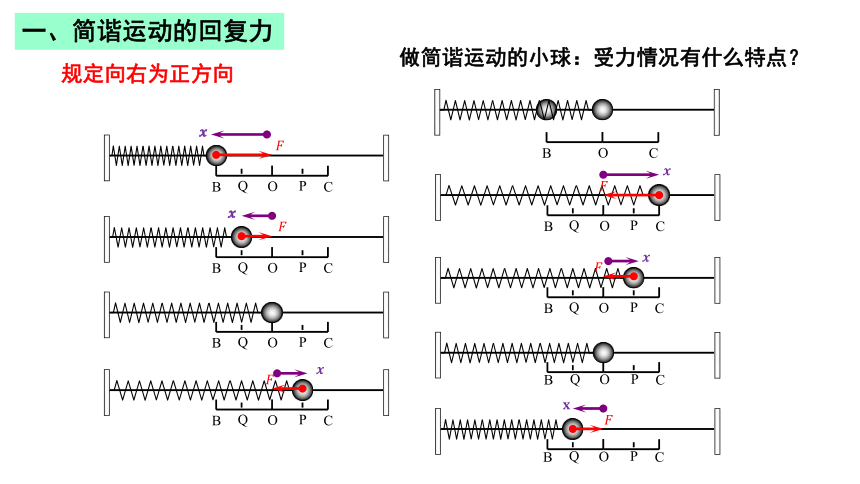
做简谐运动的小球:受力情况有什么特点?
一、简谐运动的回复力
规定向右为正方向
O
B
C
O
B
C
Q
P
O
B
C
Q
P
O
B
C
Q
P
O
B
C
Q
P
O
B
C
Q
P
O
B
C
Q
P
O
B
C
Q
P
O
C
Q
P
B
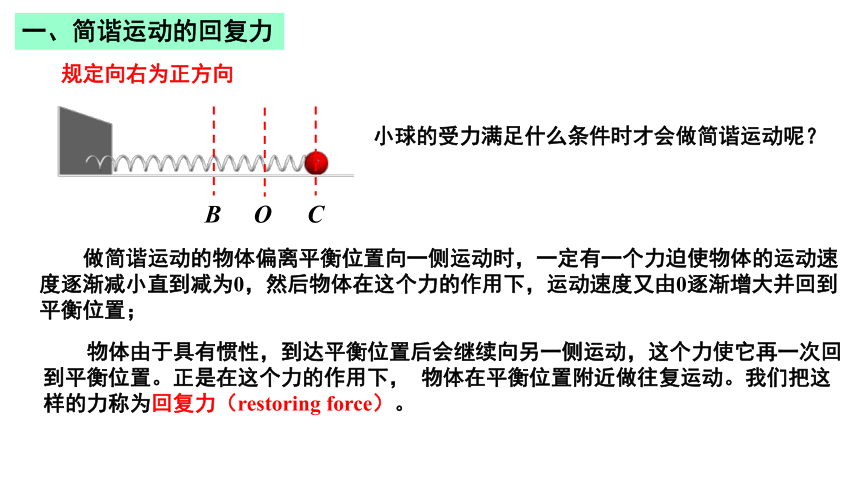
小球的受力满足什么条件时才会做简谐运动呢?
C
B
O
规定向右为正方向
做简谐运动的物体偏离平衡位置向一侧运动时,一定有一个力迫使物体的运动速度逐渐减小直到减为0,然后物体在这个力的作用下,运动速度又由0逐渐增大并回到平衡位置;
一、简谐运动的回复力
物体由于具有惯性,到达平衡位置后会继续向另一侧运动,这个力使它再一次回到平衡位置。正是在这个力的作用下, 物体在平衡位置附近做往复运动。我们把这样的力称为回复力(restoring force)。
一、简谐运动的回复力
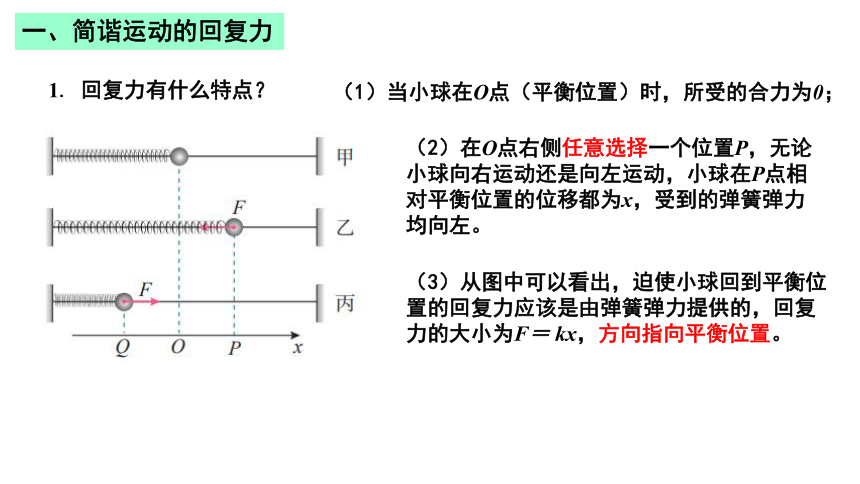
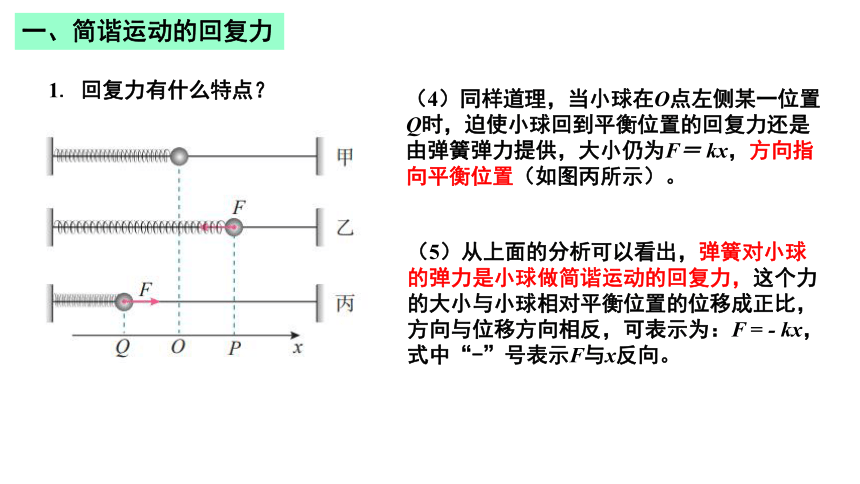
1. 回复力有什么特点?
(1)当小球在O点(平衡位置)时,所受的合力为0;
(2)在O点右侧任意选择一个位置P,无论小球向右运动还是向左运动,小球在P点相对平衡位置的位移都为x,受到的弹簧弹力均向左。
(3)从图中可以看出,迫使小球回到平衡位置的回复力应该是由弹簧弹力提供的,回复力的大小为F= kx,方向指向平衡位置。
一、简谐运动的回复力
1. 回复力有什么特点?
(4)同样道理,当小球在O点左侧某一位置Q时,迫使小球回到平衡位置的回复力还是由弹簧弹力提供,大小仍为F= kx,方向指向平衡位置(如图丙所示)。
(5)从上面的分析可以看出,弹簧对小球的弹力是小球做简谐运动的回复力,这个力的大小与小球相对平衡位置的位移成正比,方向与位移方向相反,可表示为:F = - kx, 式中“-”号表示F与x反向。
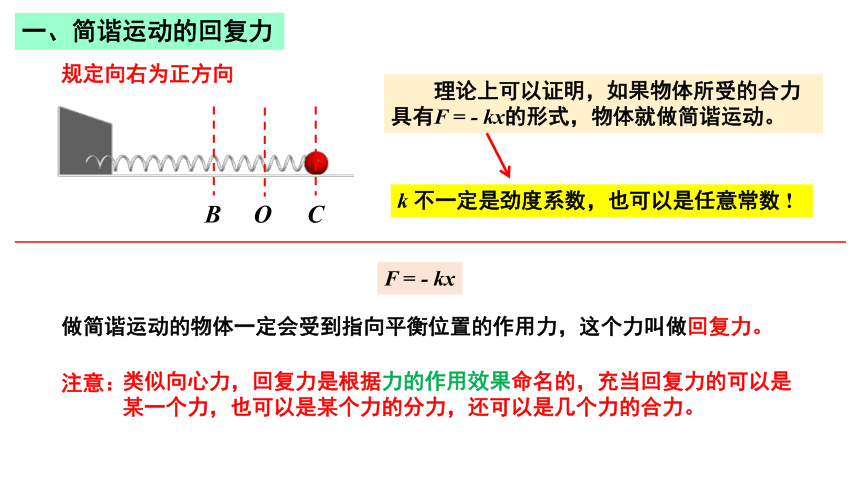
理论上可以证明,如果物体所受的合力具有F = - kx的形式,物体就做简谐运动。
一、简谐运动的回复力
C
B
O
规定向右为正方向
做简谐运动的物体一定会受到指向平衡位置的作用力,
这个力叫做回复力。
注意:
类似向心力,回复力是根据力的作用效果命名的,充当回复力的可以是某一个力,也可以是某个力的分力,还可以是几个力的合力。
k 不一定是劲度系数,也可以是任意常数 !
F = - kx
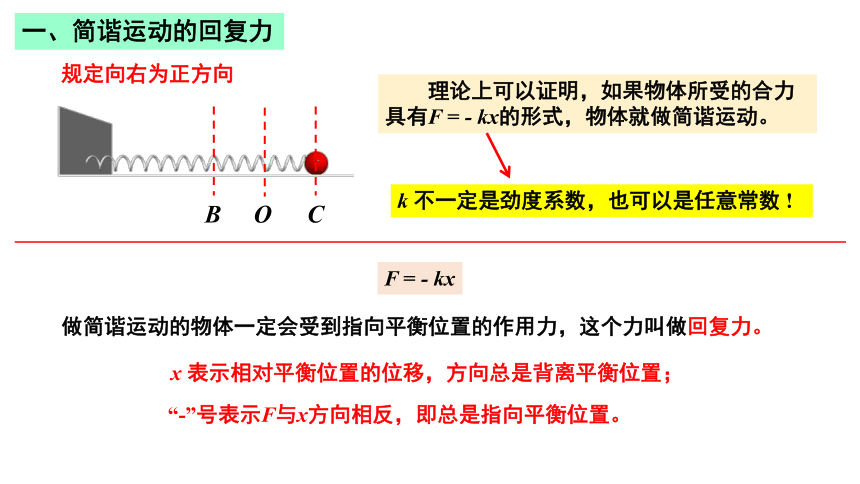
理论上可以证明,如果物体所受的合力具有F = - kx的形式,物体就做简谐运动。
一、简谐运动的回复力
C
B
O
规定向右为正方向
x 表示相对平衡位置的位移,方向总是背离平衡位置;
“-”号表示F与x方向相反,即总是指向平衡位置。
k 不一定是劲度系数,也可以是任意常数 !
做简谐运动的物体一定会受到指向平衡位置的作用力,
这个力叫做回复力。
F = - kx
理论上可以证明,如果物体所受的合力具有F = - kx的形式,物体就做简谐运动。
一、简谐运动的回复力
C
B
O
规定向右为正方向
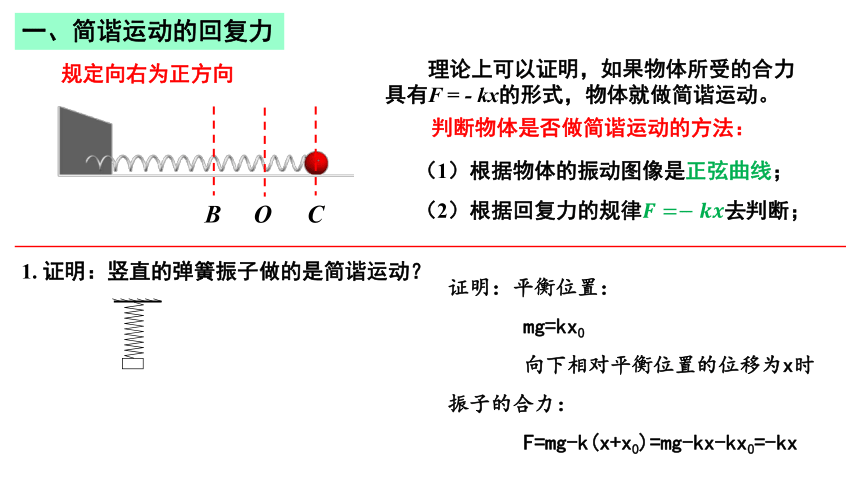
判断物体是否做简谐运动的方法:
(2)根据回复力的规律去判断;
(1)根据物体的振动图像是正弦曲线;
1. 证明:竖直的弹簧振子做的是简谐运动?
证明:平衡位置:
mg=kx0
向下相对平衡位置的位移为x时振子的合力:
F=mg-k(x+x0)=mg-kx-kx0=-kx
理论上可以证明,如果物体所受的合力具有F = - kx的形式,物体就做简谐运动。
一、简谐运动的回复力
C
B
O
规定向右为正方向
判断物体是否做简谐运动的方法:
(2)根据回复力的规律去判断;
(1)根据物体的振动图像是正弦曲线;
2. 把倾角为θ的光滑斜面上的小球沿斜面拉下一段距离,然后松开。假设空气阻力可忽略不计,试证明小球的运动是简谐运动。
证明:平衡位置:
mgsinθ=kx0
向下相对平衡位置的位移为x时振子的合力:
F=mgsinθ-k(x+x0)=mgsinθ-kx-kx0=-kx
一、简谐运动的回复力
3. 粗细均匀的一根木筷,下端绕几圈铁丝,竖直浮在较大的装有水的杯中。 把木筷往上提起一段距离后放手,木筷就在水中上下振动。
证明:是简谐运动?
空气阻力可忽略。
证明:平衡位置:
mg=ρɡsx0
向下相对平衡位置的位移为x时振子的合力:
F=mg-ρɡs(x+x0)=mg-ρɡsx-ρɡsx0=-ρɡsx=-kx
一、简谐运动的回复力
4. 光滑圆弧面上有一个小球,把它从最低点移开一小段距离,放手后,小球以最低点为平衡位置左右振动。
证明:是简谐运动?
空气阻力可忽略。
证明:小球重力沿切线方向分力提供回复力:
F回=-mgsinθ=-mgx/R=-kx
二、简谐运动的能量
C
B
O
规定向右为正方向
弹簧振子的能量变化具有什么规律呢?
小球的速度在不断变化
动能在变化;
弹簧的伸长量或压缩量在不断变化
势能也在变化。
假设P、Q 为最大位移处:
二、简谐运动的能量
弹性势能的大小取决于弹簧的形变量。
理论上可以证明,在弹簧振子运动的任意位置,系统的动能与势能之和都是一定的,遵守机械能守恒定律。
二、简谐运动的能量
小球到达最大位移时,动能为O,势能最大。
小球通过平衡位置时,动能最大,势能为O。
二、简谐运动的能量
实际的运动都有一定的能量损耗,所以简谐运动是一种理想化的模型。
当小球运动到最大位移时,动能为0,弹性势能最大,系统的机械能等于最大弹性势能。对于弹簧劲度系数和小球质量都一定的系统,振幅越大,机械能越大。
C
B
O
规定向右为正方向
物体处于最大位移处,
速度为零,动能为零,只有势能。
三、练习与应用
4. 做简谐运动的物体经过A点时,加速度的大小是2 m/s2,方向指向B点;当它经过B点时,加速度的大小是3 m/s2,方向指向A点。若AB之间的距离是10 cm,请确定它的平衡位置。
三、练习与应用
5. 图为某物体做简谐运动的图像,在 0~1.5 s 范围内回答下列问题。
(1)哪些时刻物体的回复力与 0.4 s 时的回复力相同?
(2)哪些时刻物体的速度与 0.4 s 时的速度相同?
三、练习与应用
5. 图为某物体做简谐运动的图像,在 0~1.5 s 范围内回答下列问题。
(3)哪些时刻的动能与 0.4 s 时的动能相同?
(4)哪段时间的加速度在减小?
(5)哪段时间的势能在增大?
简谐运动与圆的故事
四、有趣的事情…
有趣的是:
绿色小球做匀速周周运动一圈
红色振子做简谐运动一个周期
匀速圆周运动和简谐运动肯定有着密切的联系
有趣的事发生了…
小球和振子任意时刻均在同一竖直线上
简谐运动与圆的故事
质点在x轴上投影的运动是简谐振动
简谐振动的周期与周圆运动的周期相同
(具有普遍性,对所有的简谐运动都适用)
简谐振动的位移随时间变化:
四、有趣的事情…
w
O
x
A
第二章 机械振动
2.3 简谐运动的回复力和能量
restoring force and energy
做简谐运动的小球:受力情况有什么特点?
一、简谐运动的回复力
C
B
O
规定向右为正方向
胡克定律:F = -k x
做简谐运动的小球:受力情况有什么特点?
一、简谐运动的回复力
规定向右为正方向
O
B
C
O
B
C
Q
P
O
B
C
Q
P
O
B
C
Q
P
O
B
C
Q
P
O
B
C
Q
P
O
B
C
Q
P
O
B
C
Q
P
O
C
Q
P
B
小球的受力满足什么条件时才会做简谐运动呢?
C
B
O
规定向右为正方向
做简谐运动的物体偏离平衡位置向一侧运动时,一定有一个力迫使物体的运动速度逐渐减小直到减为0,然后物体在这个力的作用下,运动速度又由0逐渐增大并回到平衡位置;
一、简谐运动的回复力
物体由于具有惯性,到达平衡位置后会继续向另一侧运动,这个力使它再一次回到平衡位置。正是在这个力的作用下, 物体在平衡位置附近做往复运动。我们把这样的力称为回复力(restoring force)。
一、简谐运动的回复力
1. 回复力有什么特点?
(1)当小球在O点(平衡位置)时,所受的合力为0;
(2)在O点右侧任意选择一个位置P,无论小球向右运动还是向左运动,小球在P点相对平衡位置的位移都为x,受到的弹簧弹力均向左。
(3)从图中可以看出,迫使小球回到平衡位置的回复力应该是由弹簧弹力提供的,回复力的大小为F= kx,方向指向平衡位置。
一、简谐运动的回复力
1. 回复力有什么特点?
(4)同样道理,当小球在O点左侧某一位置Q时,迫使小球回到平衡位置的回复力还是由弹簧弹力提供,大小仍为F= kx,方向指向平衡位置(如图丙所示)。
(5)从上面的分析可以看出,弹簧对小球的弹力是小球做简谐运动的回复力,这个力的大小与小球相对平衡位置的位移成正比,方向与位移方向相反,可表示为:F = - kx, 式中“-”号表示F与x反向。
理论上可以证明,如果物体所受的合力具有F = - kx的形式,物体就做简谐运动。
一、简谐运动的回复力
C
B
O
规定向右为正方向
做简谐运动的物体一定会受到指向平衡位置的作用力,
这个力叫做回复力。
注意:
类似向心力,回复力是根据力的作用效果命名的,充当回复力的可以是某一个力,也可以是某个力的分力,还可以是几个力的合力。
k 不一定是劲度系数,也可以是任意常数 !
F = - kx
理论上可以证明,如果物体所受的合力具有F = - kx的形式,物体就做简谐运动。
一、简谐运动的回复力
C
B
O
规定向右为正方向
x 表示相对平衡位置的位移,方向总是背离平衡位置;
“-”号表示F与x方向相反,即总是指向平衡位置。
k 不一定是劲度系数,也可以是任意常数 !
做简谐运动的物体一定会受到指向平衡位置的作用力,
这个力叫做回复力。
F = - kx
理论上可以证明,如果物体所受的合力具有F = - kx的形式,物体就做简谐运动。
一、简谐运动的回复力
C
B
O
规定向右为正方向
判断物体是否做简谐运动的方法:
(2)根据回复力的规律去判断;
(1)根据物体的振动图像是正弦曲线;
1. 证明:竖直的弹簧振子做的是简谐运动?
证明:平衡位置:
mg=kx0
向下相对平衡位置的位移为x时振子的合力:
F=mg-k(x+x0)=mg-kx-kx0=-kx
理论上可以证明,如果物体所受的合力具有F = - kx的形式,物体就做简谐运动。
一、简谐运动的回复力
C
B
O
规定向右为正方向
判断物体是否做简谐运动的方法:
(2)根据回复力的规律去判断;
(1)根据物体的振动图像是正弦曲线;
2. 把倾角为θ的光滑斜面上的小球沿斜面拉下一段距离,然后松开。假设空气阻力可忽略不计,试证明小球的运动是简谐运动。
证明:平衡位置:
mgsinθ=kx0
向下相对平衡位置的位移为x时振子的合力:
F=mgsinθ-k(x+x0)=mgsinθ-kx-kx0=-kx
一、简谐运动的回复力
3. 粗细均匀的一根木筷,下端绕几圈铁丝,竖直浮在较大的装有水的杯中。 把木筷往上提起一段距离后放手,木筷就在水中上下振动。
证明:是简谐运动?
空气阻力可忽略。
证明:平衡位置:
mg=ρɡsx0
向下相对平衡位置的位移为x时振子的合力:
F=mg-ρɡs(x+x0)=mg-ρɡsx-ρɡsx0=-ρɡsx=-kx
一、简谐运动的回复力
4. 光滑圆弧面上有一个小球,把它从最低点移开一小段距离,放手后,小球以最低点为平衡位置左右振动。
证明:是简谐运动?
空气阻力可忽略。
证明:小球重力沿切线方向分力提供回复力:
F回=-mgsinθ=-mgx/R=-kx
二、简谐运动的能量
C
B
O
规定向右为正方向
弹簧振子的能量变化具有什么规律呢?
小球的速度在不断变化
动能在变化;
弹簧的伸长量或压缩量在不断变化
势能也在变化。
假设P、Q 为最大位移处:
二、简谐运动的能量
弹性势能的大小取决于弹簧的形变量。
理论上可以证明,在弹簧振子运动的任意位置,系统的动能与势能之和都是一定的,遵守机械能守恒定律。
二、简谐运动的能量
小球到达最大位移时,动能为O,势能最大。
小球通过平衡位置时,动能最大,势能为O。
二、简谐运动的能量
实际的运动都有一定的能量损耗,所以简谐运动是一种理想化的模型。
当小球运动到最大位移时,动能为0,弹性势能最大,系统的机械能等于最大弹性势能。对于弹簧劲度系数和小球质量都一定的系统,振幅越大,机械能越大。
C
B
O
规定向右为正方向
物体处于最大位移处,
速度为零,动能为零,只有势能。
三、练习与应用
4. 做简谐运动的物体经过A点时,加速度的大小是2 m/s2,方向指向B点;当它经过B点时,加速度的大小是3 m/s2,方向指向A点。若AB之间的距离是10 cm,请确定它的平衡位置。
三、练习与应用
5. 图为某物体做简谐运动的图像,在 0~1.5 s 范围内回答下列问题。
(1)哪些时刻物体的回复力与 0.4 s 时的回复力相同?
(2)哪些时刻物体的速度与 0.4 s 时的速度相同?
三、练习与应用
5. 图为某物体做简谐运动的图像,在 0~1.5 s 范围内回答下列问题。
(3)哪些时刻的动能与 0.4 s 时的动能相同?
(4)哪段时间的加速度在减小?
(5)哪段时间的势能在增大?
简谐运动与圆的故事
四、有趣的事情…
有趣的是:
绿色小球做匀速周周运动一圈
红色振子做简谐运动一个周期
匀速圆周运动和简谐运动肯定有着密切的联系
有趣的事发生了…
小球和振子任意时刻均在同一竖直线上
简谐运动与圆的故事
质点在x轴上投影的运动是简谐振动
简谐振动的周期与周圆运动的周期相同
(具有普遍性,对所有的简谐运动都适用)
简谐振动的位移随时间变化:
四、有趣的事情…
w
O
x
A
