人教A版(2019)数学高二下 期末复习-导数(含解析)
文档属性
| 名称 | 人教A版(2019)数学高二下 期末复习-导数(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-05 14:41:42 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
导数
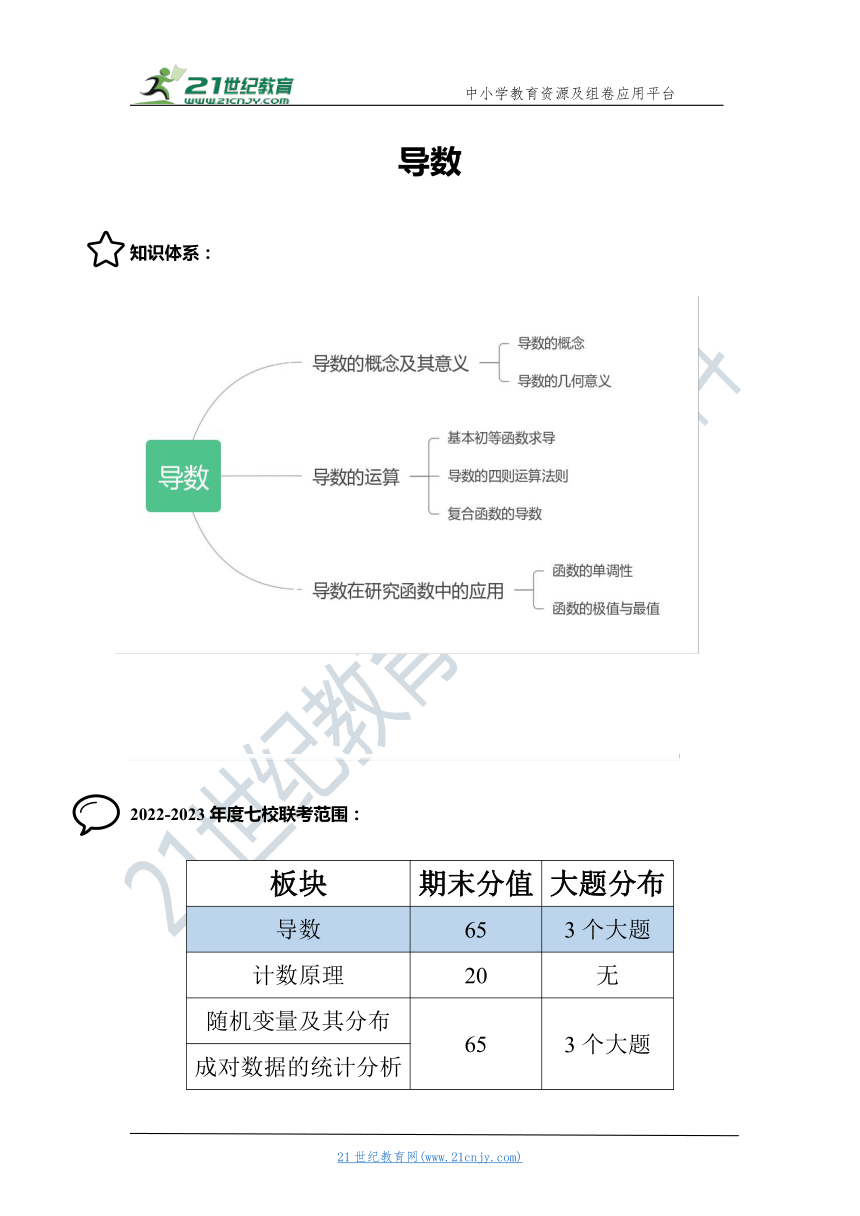
知识体系:
2022-2023年度七校联考范围:
板块 期末分值 大题分布
导数 65 3个大题
计数原理 20 无
随机变量及其分布 65 3个大题
成对数据的统计分析
21世纪教育网(www.21cnjy.com)
知识清单:
一、变化率和导数
1.平均变化率
对于函数,设自变量从变化到,相应地,函数值就从变化到,这时,的变化量为,的变化量为,我们把比值,即叫做函数从变化到的平均变化率。
2.导数(瞬时变化率)
如果当时,平均变化率无限趋近于一个确定的值,即有极限,则称在处可导,并把这个确定的值叫做在处的导数(也称为瞬时变化率),记作或,即。
3.导数的几何意义与切线
(1)导数的几何意义:函数在处的导数是函数在该点处的切线的斜率,即。
(2)切线问题
①在函数上某点的切线方程
【步骤】:
⒈求
⒉代入得斜率:
⒊点斜式得方程:
②过函数外一点作函数的切线
设该切线与函数相切的切点为,
则切线方程为,……………………………(*)
该切线经过点,故
解方程算出的值,代回(*)式即可
③切线方程的含参问题:
列出与切线相关的3个核心方程
⒈
⒉切点在切线上
⒊切点在曲线上
注:若题目中没有给出切点,则立马设切点
④求函数和函数的公切线
设公切线与的切点横坐标为,则切线方程
公切线与的切点横坐标为,则切线方程,
两条切线方程应相同,即斜率和截距均相等,,解方程算出,的值即可
5.导函数(导数)的概念
当变化时,就是的函数,我们称它为的导函数(简称导数),的导函数有时也记作,。
二、导数的计算
1.基本初等函数的导数
(1)若(为常数),则;
(2)若(,且),则;
(3)若,则;
(4)若,则;
(5)若(,且),则,特别地,若,则;
(6)若(,且),则,
特别地,若,则。
2.导数的四则运算法则
一般地,对于两个函数和,我们有如下法则:
(1);
(2);
(3),
特别地,若为常数,则。
3.复合函数的导数
一般地,对于由函数和复合而成的函数,它的导数与函数,的导数间的关系为。
三、导数与单调性
1.函数单调性和导数的关系
一般地,函数的单调性和导函数的正负之间具有如下的关系:
在某个区间上,如果,那么函数在区间上单调递增;
在某个区间上,如果,那么函数在区间上单调递减。
记忆口诀:导函数看正负,原函数看增减
2.求函数单调性的步骤
①求定义域
②求导,画草图
③根据正负得单调区间
3.含参函数单调性的讨论步骤(当导函数有效部分为含参二次函数时)
4.已知函数单调性求参数
可导函数在区间上单调递增
可导函数在区间上单调递减
【方法小结】:
⑴在R上单调(导函数为二次函数型),判别式法
⑵在上单调,分参法(能分则分)或整体法(不能分参时)
四、导数与极最值
1.极值点和极值
如果函数在附近的左侧,且在附近的右侧,则称为函数的极小值点,叫做函数的极小值;
如果函数在附近的左侧,且在附近的右侧,则称为函数的极大值点,叫做函数的极大值。
记忆技巧:极值点出现在原函数单调性发生转变时,导函数正负发生转变时。
2.最大值和最小值
函数在闭区间上一定存在最大值和最小值,比较所有极值和端点的函数值,其中最大的为函数的最大值,最小的为函数的最小值。
3.已知极最值反求参数
函数在处取得极值:
【小结】:
⑴在开区间上有最值在有极值(极值点)
⑵无极值点单调
五、函数构造
原理:利用的单调性解不等式
条件:①含不等式;②解析式未知
规律:①同时出现和时,构造乘除法;②加法构造乘法,减法构造除法(不能放分母);③当前有时,构造含的幂函数;当前无时,构造含的指数函数;④其他形式:如含,,等,按照特征构造即可。
1.
构造形式:
2.
构造形式:
特别地,当时,
3.
构造形式:
特别地,当时,
4.
构造形式:
特别地,当时,
5.
构造形式:
特别地,当时,
6.
构造形式:
7.
构造形式:
8.
构造形式:
9.
构造形式:
10.
构造形式:
11.
构造形式:
12.
构造形式:
13.
构造形式:
六、导数压轴大题技巧
1.极值点偏移母题常规六解:
函数,若存在,使得。
求证:
梳理:,故,;
不妨设则
法一:左右构造
要证:,只需证
构造函数,,
得证。
法二:居中构造
构造函数
故
又
又,故
得证。
法三:对均不等式
由题意
由对均不等式(考试需证明),得。
得证。
法四:齐次化
由题意
要证:,只需证、
令,即证,,显然成立(考试需构造函数证明)。
得证。
法五:比值换元
设
令,则
要证,只需证显然成立(考试需构造函数证明)。
得证。
法六:二次函数拟合
构造函数
令
则,且
又
所以
又,
则
。
得证。
小结:在平时练习中,以法一法二为主;法一与法二为对称构造,法四与法五为齐次化后比值换元。
2.隐零点问题
导数隐零点问题的破解策略:在解导数综合题时,经常会碰到:导函数存在零点,但零点不能求出来,这种零点我们称之为隐零点,相应的问题称为隐零点问题。此时,一般虚设零点(隐零点),通过对方程变形、因式分解判断单调性,或通过过渡;再研究的性质,对隐零点进行估计,回避隐零点,再结合题目其他条件,最终解决问题。对于指对混合问题,下列恒等式:
,,,,会灵活运用,解题也往往会事半功倍此外,如果将问题适当转化也可以回避隐零点。比如:转化为 转化为
求解步骤:
第一步:求导
第二步:判断的增减性
求二阶导
一般是单增或单减
第三步:设的零点,根据零点存在性定理卡出的范围
化为同一阶
第四步:写出,把第三步的结果代入即可求值
以下列例题进行说明:
已知函数.
(1)当时,求曲线在点,处的切线方程;
(2)若在区间,各恰有一个零点,求的取值范围.
解:(1)当时,,则,
,
又,
所求切线方程为;
(2),
若,当时,,单调递增,则,不合题意;
故,,令,注意到,
令,解得或,令,解得,
在单调递减,在单调递增,且时,,
①若,当时,,单调递增,不合题意;
②若,(1),则存在,使得,
且当时,,单调递减,则,
当时,,,则由零点存在性定理可知在,上存在一个根,
当时,,单调递减,,
当时,,,则由零点存在性定理可知在上存在一个根.
综上,实数的取值范围为
期末押题:
一.选择题(共3小题)
1.函数的单调递增区间是
A. B. C. D.
2.已知过点可以作曲线的两条切线,则实数的取值范围是
A. B.,,
C.,, D.,,
3.已知是函数的导函数,,且对于任意的有.则下列不等式一定成立的是
A. B.
C. D.
二.多选题(共2小题)
4.函数,下列对函数的性质描述正确的是
A.函数的图象关于点对称
B.若,则函数有极值点
C.若,函数在区间单调递减
D.若函数有且只有3个零点,则的取值范围是
5.已知函数,,则下列结论正确的有
A.函数的极小值点是1
B.若函数在,上是单调的,则
C.若不等式恰有两个正整数解,则
D.若函数与的值域相同,则实数的取值范围是
三.填空题(共1小题)
6.已知曲线,则该曲线在原点处的切线方程为 .
四.解答题(共3小题)
7.设函数.
(1)若是函数的极值点,求在上的最大值;
(2)若曲线在处的切线与曲线也相切,求实数的值.
8.已知函数,.
(1)证明:;
(2)若有两个不同的零点,,且,证明:.
9.已知函数,其中为自然对数的底数,
(1)若对,恒成立,求实数的值;
(2)在(1)的条件下,
(ⅰ)证明:有三个根,,;
(ⅱ)设,请从以下不等式中任选一个进行证明:
①;
②.
.参考数据:,.
参考答案与试题解析
一.选择题(共3小题)
1.【解答】解:因为定义域是,且,
令,解得:,
故单调递增区间是,
故选:.
2.【解答】解:设切点是,,,即,而,
故切线斜率,切线方程是,
又因为切线经过点,故,显然,
则,在上有两个交点,
令,设,则,令得,,
所以当时,,单调递增,当时,,单调递减,
当时,,单调递减,当时,,单调递增,
又,(1),且时,,时,,时,,时,,
所以有两个交点,则或,故实数的取值范围是,,.
故选:.
3.【解答】解:由,
故是偶函数,
由函数对于任意的满足,
令,,
故,
故在递增,是偶函数,
故(1),
又,,,
(1),,
即,
故只有答案成立,其他错误,
故选:.
二.多选题(共2小题)
4.【解答】解:对于,,
,函数的图像关于点对称,故选项正确;
对于:由,
当时,,函数在定义域内为增函数,
此时函数没有极值点,故选项错误;
对于:当时,由,解得:,
又时,,函数在区间递增,故选项错误;
对于:由,
当时,,函数在定义域内为增函数,
故不存在三个零点,不符合题意,
当时,由,解得:,
又时,,
,时,,,时,,
函数在递增,在,递减,在,递增,
函数的极小值是,极大值是,
函数有个不同的零点,
,解得:,故选项正确,
故选:.
5.【解答】解:对于,的定义域为,
当时,,所以,单调递减;
当时,,所以,单调递增.
又(1),所以函数的极小值点为1.故正确;
对于,当,时,在,上是单调的,所以错误;
对于,,作出函数和的图象,
所以,解得,故正确;
对于,(1),又当时,,
所以的值域为,,又因为与的值域相同,
所以,,,所以.故正确;
故选:.
三.填空题(共1小题)
6.【解答】解:由,
得,
,
则曲线在原点处的切线方程为.
故答案为:.
四.解答题(共3小题)
7.【解答】解:(1)因为,所以,,
因为是函数的极值点,所以(2),得,
此时,,
当时,,当时,,
所以在上为减函数,在上为增函数,
所以是的一个极小值点,所以符合题意.
由以上可知,在,上为减函数,在,上为增函数,
又,(e),
所以(e),
所以在,上的最大值为.
(2)由(1)知,,,所以(1),
又(1),所以切线,即,
假设直线与曲线切于,,
因为,所以,
又,
所以在,处的切线方程为,
即,
因为直线与直线重合,
所以,得,
解得或.
8.【解答】证明:(1)令,
,
所以在上,在上,
所以(2),
所以;
(2)令,,
,由(1)知,
且在上单减,在上单增,
要证,即证,又,
故只需证明,
令
,
,
则,
,
,
,
,(2),
(2),
原不等式成立.
9.【解答】解:(1)由对,恒成立,可得,
由,得,
①当时,,所以在上单调递增,
而当时,,不满足题意,
②当时,由,得,
当时,,当时,,
所以在上递减,在上递增,
所以,
设(a),则(a),
因为(a),令(a),则,
当时,(a),当时,(a),
所以(a)在上递增,在上递减,
所以(a)(1),
综上(a),则
(2)证明:由(1)可知,令,则.
先解,
令,
在单调递减,在单调递增.
,,,
,
使得,即有两个零点以及,如图:
再解,
当时,即,由(1)可知,
当时,有,显然是其中一根,
,,
所以使得,
所以有三个零点,0,,如图所示.
由题,,,所以,,
且,
若选①:要证,即证,
又由(1)时取等),
令,得(当时取等),
所以有,
所以只需证,而,
所以只需证,
因为,所以,所以显然成立,得证.
若选②:即证:,
因为,
所以即证,又由(1)时取等),
令,得(当时取等),
所以有,所以即证,即,得证.
21世纪教育网(www.21cnjy.com)
导数
知识体系:
2022-2023年度七校联考范围:
板块 期末分值 大题分布
导数 65 3个大题
计数原理 20 无
随机变量及其分布 65 3个大题
成对数据的统计分析
21世纪教育网(www.21cnjy.com)
知识清单:
一、变化率和导数
1.平均变化率
对于函数,设自变量从变化到,相应地,函数值就从变化到,这时,的变化量为,的变化量为,我们把比值,即叫做函数从变化到的平均变化率。
2.导数(瞬时变化率)
如果当时,平均变化率无限趋近于一个确定的值,即有极限,则称在处可导,并把这个确定的值叫做在处的导数(也称为瞬时变化率),记作或,即。
3.导数的几何意义与切线
(1)导数的几何意义:函数在处的导数是函数在该点处的切线的斜率,即。
(2)切线问题
①在函数上某点的切线方程
【步骤】:
⒈求
⒉代入得斜率:
⒊点斜式得方程:
②过函数外一点作函数的切线
设该切线与函数相切的切点为,
则切线方程为,……………………………(*)
该切线经过点,故
解方程算出的值,代回(*)式即可
③切线方程的含参问题:
列出与切线相关的3个核心方程
⒈
⒉切点在切线上
⒊切点在曲线上
注:若题目中没有给出切点,则立马设切点
④求函数和函数的公切线
设公切线与的切点横坐标为,则切线方程
公切线与的切点横坐标为,则切线方程,
两条切线方程应相同,即斜率和截距均相等,,解方程算出,的值即可
5.导函数(导数)的概念
当变化时,就是的函数,我们称它为的导函数(简称导数),的导函数有时也记作,。
二、导数的计算
1.基本初等函数的导数
(1)若(为常数),则;
(2)若(,且),则;
(3)若,则;
(4)若,则;
(5)若(,且),则,特别地,若,则;
(6)若(,且),则,
特别地,若,则。
2.导数的四则运算法则
一般地,对于两个函数和,我们有如下法则:
(1);
(2);
(3),
特别地,若为常数,则。
3.复合函数的导数
一般地,对于由函数和复合而成的函数,它的导数与函数,的导数间的关系为。
三、导数与单调性
1.函数单调性和导数的关系
一般地,函数的单调性和导函数的正负之间具有如下的关系:
在某个区间上,如果,那么函数在区间上单调递增;
在某个区间上,如果,那么函数在区间上单调递减。
记忆口诀:导函数看正负,原函数看增减
2.求函数单调性的步骤
①求定义域
②求导,画草图
③根据正负得单调区间
3.含参函数单调性的讨论步骤(当导函数有效部分为含参二次函数时)
4.已知函数单调性求参数
可导函数在区间上单调递增
可导函数在区间上单调递减
【方法小结】:
⑴在R上单调(导函数为二次函数型),判别式法
⑵在上单调,分参法(能分则分)或整体法(不能分参时)
四、导数与极最值
1.极值点和极值
如果函数在附近的左侧,且在附近的右侧,则称为函数的极小值点,叫做函数的极小值;
如果函数在附近的左侧,且在附近的右侧,则称为函数的极大值点,叫做函数的极大值。
记忆技巧:极值点出现在原函数单调性发生转变时,导函数正负发生转变时。
2.最大值和最小值
函数在闭区间上一定存在最大值和最小值,比较所有极值和端点的函数值,其中最大的为函数的最大值,最小的为函数的最小值。
3.已知极最值反求参数
函数在处取得极值:
【小结】:
⑴在开区间上有最值在有极值(极值点)
⑵无极值点单调
五、函数构造
原理:利用的单调性解不等式
条件:①含不等式;②解析式未知
规律:①同时出现和时,构造乘除法;②加法构造乘法,减法构造除法(不能放分母);③当前有时,构造含的幂函数;当前无时,构造含的指数函数;④其他形式:如含,,等,按照特征构造即可。
1.
构造形式:
2.
构造形式:
特别地,当时,
3.
构造形式:
特别地,当时,
4.
构造形式:
特别地,当时,
5.
构造形式:
特别地,当时,
6.
构造形式:
7.
构造形式:
8.
构造形式:
9.
构造形式:
10.
构造形式:
11.
构造形式:
12.
构造形式:
13.
构造形式:
六、导数压轴大题技巧
1.极值点偏移母题常规六解:
函数,若存在,使得。
求证:
梳理:,故,;
不妨设则
法一:左右构造
要证:,只需证
构造函数,,
得证。
法二:居中构造
构造函数
故
又
又,故
得证。
法三:对均不等式
由题意
由对均不等式(考试需证明),得。
得证。
法四:齐次化
由题意
要证:,只需证、
令,即证,,显然成立(考试需构造函数证明)。
得证。
法五:比值换元
设
令,则
要证,只需证显然成立(考试需构造函数证明)。
得证。
法六:二次函数拟合
构造函数
令
则,且
又
所以
又,
则
。
得证。
小结:在平时练习中,以法一法二为主;法一与法二为对称构造,法四与法五为齐次化后比值换元。
2.隐零点问题
导数隐零点问题的破解策略:在解导数综合题时,经常会碰到:导函数存在零点,但零点不能求出来,这种零点我们称之为隐零点,相应的问题称为隐零点问题。此时,一般虚设零点(隐零点),通过对方程变形、因式分解判断单调性,或通过过渡;再研究的性质,对隐零点进行估计,回避隐零点,再结合题目其他条件,最终解决问题。对于指对混合问题,下列恒等式:
,,,,会灵活运用,解题也往往会事半功倍此外,如果将问题适当转化也可以回避隐零点。比如:转化为 转化为
求解步骤:
第一步:求导
第二步:判断的增减性
求二阶导
一般是单增或单减
第三步:设的零点,根据零点存在性定理卡出的范围
化为同一阶
第四步:写出,把第三步的结果代入即可求值
以下列例题进行说明:
已知函数.
(1)当时,求曲线在点,处的切线方程;
(2)若在区间,各恰有一个零点,求的取值范围.
解:(1)当时,,则,
,
又,
所求切线方程为;
(2),
若,当时,,单调递增,则,不合题意;
故,,令,注意到,
令,解得或,令,解得,
在单调递减,在单调递增,且时,,
①若,当时,,单调递增,不合题意;
②若,(1),则存在,使得,
且当时,,单调递减,则,
当时,,,则由零点存在性定理可知在,上存在一个根,
当时,,单调递减,,
当时,,,则由零点存在性定理可知在上存在一个根.
综上,实数的取值范围为
期末押题:
一.选择题(共3小题)
1.函数的单调递增区间是
A. B. C. D.
2.已知过点可以作曲线的两条切线,则实数的取值范围是
A. B.,,
C.,, D.,,
3.已知是函数的导函数,,且对于任意的有.则下列不等式一定成立的是
A. B.
C. D.
二.多选题(共2小题)
4.函数,下列对函数的性质描述正确的是
A.函数的图象关于点对称
B.若,则函数有极值点
C.若,函数在区间单调递减
D.若函数有且只有3个零点,则的取值范围是
5.已知函数,,则下列结论正确的有
A.函数的极小值点是1
B.若函数在,上是单调的,则
C.若不等式恰有两个正整数解,则
D.若函数与的值域相同,则实数的取值范围是
三.填空题(共1小题)
6.已知曲线,则该曲线在原点处的切线方程为 .
四.解答题(共3小题)
7.设函数.
(1)若是函数的极值点,求在上的最大值;
(2)若曲线在处的切线与曲线也相切,求实数的值.
8.已知函数,.
(1)证明:;
(2)若有两个不同的零点,,且,证明:.
9.已知函数,其中为自然对数的底数,
(1)若对,恒成立,求实数的值;
(2)在(1)的条件下,
(ⅰ)证明:有三个根,,;
(ⅱ)设,请从以下不等式中任选一个进行证明:
①;
②.
.参考数据:,.
参考答案与试题解析
一.选择题(共3小题)
1.【解答】解:因为定义域是,且,
令,解得:,
故单调递增区间是,
故选:.
2.【解答】解:设切点是,,,即,而,
故切线斜率,切线方程是,
又因为切线经过点,故,显然,
则,在上有两个交点,
令,设,则,令得,,
所以当时,,单调递增,当时,,单调递减,
当时,,单调递减,当时,,单调递增,
又,(1),且时,,时,,时,,时,,
所以有两个交点,则或,故实数的取值范围是,,.
故选:.
3.【解答】解:由,
故是偶函数,
由函数对于任意的满足,
令,,
故,
故在递增,是偶函数,
故(1),
又,,,
(1),,
即,
故只有答案成立,其他错误,
故选:.
二.多选题(共2小题)
4.【解答】解:对于,,
,函数的图像关于点对称,故选项正确;
对于:由,
当时,,函数在定义域内为增函数,
此时函数没有极值点,故选项错误;
对于:当时,由,解得:,
又时,,函数在区间递增,故选项错误;
对于:由,
当时,,函数在定义域内为增函数,
故不存在三个零点,不符合题意,
当时,由,解得:,
又时,,
,时,,,时,,
函数在递增,在,递减,在,递增,
函数的极小值是,极大值是,
函数有个不同的零点,
,解得:,故选项正确,
故选:.
5.【解答】解:对于,的定义域为,
当时,,所以,单调递减;
当时,,所以,单调递增.
又(1),所以函数的极小值点为1.故正确;
对于,当,时,在,上是单调的,所以错误;
对于,,作出函数和的图象,
所以,解得,故正确;
对于,(1),又当时,,
所以的值域为,,又因为与的值域相同,
所以,,,所以.故正确;
故选:.
三.填空题(共1小题)
6.【解答】解:由,
得,
,
则曲线在原点处的切线方程为.
故答案为:.
四.解答题(共3小题)
7.【解答】解:(1)因为,所以,,
因为是函数的极值点,所以(2),得,
此时,,
当时,,当时,,
所以在上为减函数,在上为增函数,
所以是的一个极小值点,所以符合题意.
由以上可知,在,上为减函数,在,上为增函数,
又,(e),
所以(e),
所以在,上的最大值为.
(2)由(1)知,,,所以(1),
又(1),所以切线,即,
假设直线与曲线切于,,
因为,所以,
又,
所以在,处的切线方程为,
即,
因为直线与直线重合,
所以,得,
解得或.
8.【解答】证明:(1)令,
,
所以在上,在上,
所以(2),
所以;
(2)令,,
,由(1)知,
且在上单减,在上单增,
要证,即证,又,
故只需证明,
令
,
,
则,
,
,
,
,(2),
(2),
原不等式成立.
9.【解答】解:(1)由对,恒成立,可得,
由,得,
①当时,,所以在上单调递增,
而当时,,不满足题意,
②当时,由,得,
当时,,当时,,
所以在上递减,在上递增,
所以,
设(a),则(a),
因为(a),令(a),则,
当时,(a),当时,(a),
所以(a)在上递增,在上递减,
所以(a)(1),
综上(a),则
(2)证明:由(1)可知,令,则.
先解,
令,
在单调递减,在单调递增.
,,,
,
使得,即有两个零点以及,如图:
再解,
当时,即,由(1)可知,
当时,有,显然是其中一根,
,,
所以使得,
所以有三个零点,0,,如图所示.
由题,,,所以,,
且,
若选①:要证,即证,
又由(1)时取等),
令,得(当时取等),
所以有,
所以只需证,而,
所以只需证,
因为,所以,所以显然成立,得证.
若选②:即证:,
因为,
所以即证,又由(1)时取等),
令,得(当时取等),
所以有,所以即证,即,得证.
同课章节目录
