山东省济南天桥区黄河双语学校2023年5月高一下学期数学月考考试试卷(含答案)
文档属性
| 名称 | 山东省济南天桥区黄河双语学校2023年5月高一下学期数学月考考试试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 324.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-05 15:36:22 | ||
图片预览


文档简介
高一下学期数学月考试卷
(满分150分 时间:120分钟)
一.单选题。(共8小题,每小题5分,共40分)
1.已知(1+i)z=3-i,其中i为虚数单位,则=( )
A.5 B. C.2 D.
2.已知复数z=(i为虚数单位),则z的共轭复数在复平面内对应的点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.如图,正方形O’A’B’C’的边长为1,它是一个水平放置的平面图形的直观图,则原图形的周长是( )
A.4 B.6 C.8 D.2+2
(第3题图) (第4题图)
4.如图,在长方体ABCD-A1B1C1D1中,AB=BC=2,AA1=1,则AC1与平面A1B1C1D1所成角的正弦值为( )
A. B. C. D.
5.设b,c表示两条直线,α,β表示两个平面,下列命题正确的是( )
A.若b∥α,cα,则b∥c B.若bα,b∥c,则cα
C.若c∥α,α⊥β,则c⊥β D.若c∥α,c⊥β,则α⊥β
6.已知圆锥的顶点为P,底面圆心为O,若过直线OP的平面截圆锥所得的截面是面积为4的等腰直角三角形,则该圆锥的侧面积为( )
A.4π B.2π C.4π D.(4+4)π
7.已知圆锥的母线长为10,侧面展开图的圆心角为,则该圆锥的体积为( )
A.π B.32π C.16π D.π
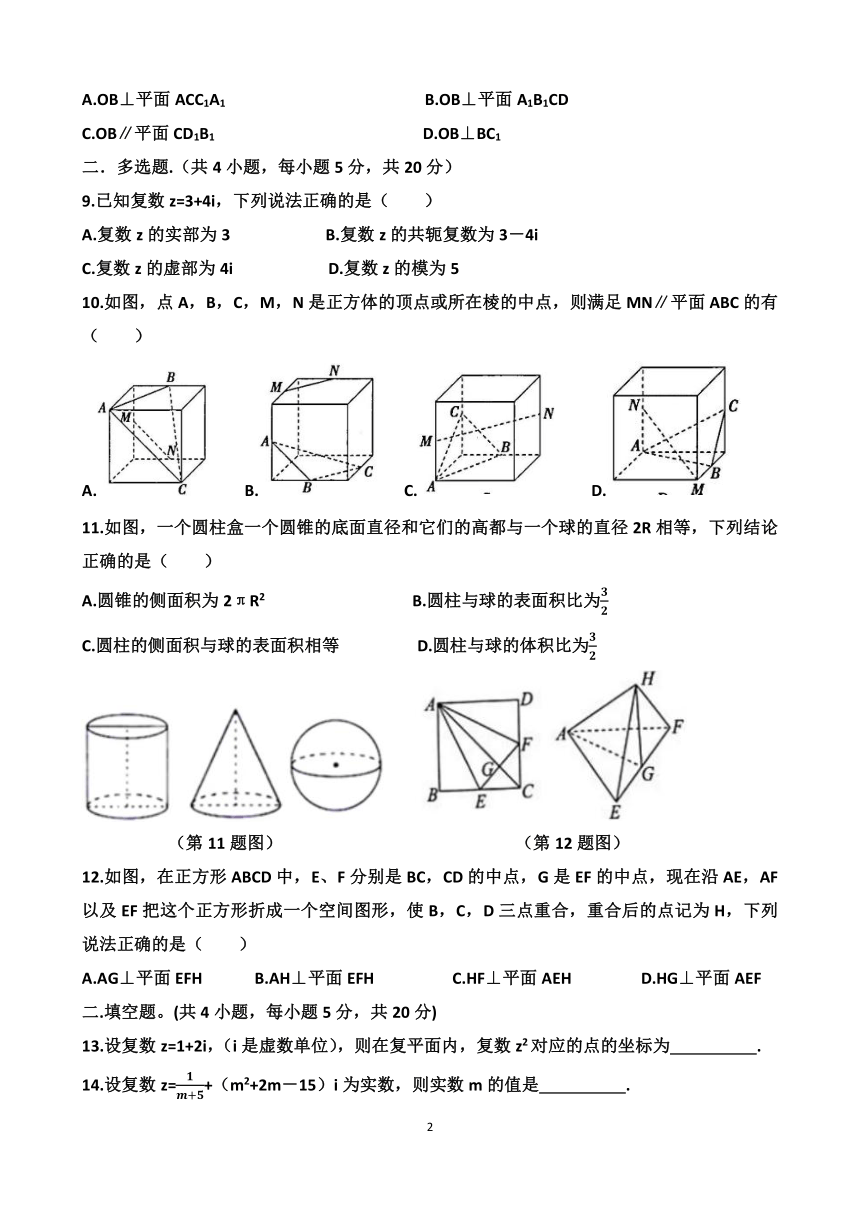
8.已知在正方体中,AD1,A1D交于点O,则( )
A.OB⊥平面ACC1A1 B.OB⊥平面A1B1CD
C.OB∥平面CD1B1 D.OB⊥BC1
二.多选题.(共4小题,每小题5分,共20分)
9.已知复数z=3+4i,下列说法正确的是( )
A.复数z的实部为3 B.复数z的共轭复数为3-4i
C.复数z的虚部为4i D.复数z的模为5
10.如图,点A,B,C,M,N是正方体的顶点或所在棱的中点,则满足MN∥平面ABC的有( )
A. B. C. D.
11.如图,一个圆柱盒一个圆锥的底面直径和它们的高都与一个球的直径2R相等,下列结论正确的是( )
A.圆锥的侧面积为2πR2 B.圆柱与球的表面积比为
C.圆柱的侧面积与球的表面积相等 D.圆柱与球的体积比为
(第11题图) (第12题图)
12.如图,在正方形ABCD中,E、F分别是BC,CD的中点,G是EF的中点,现在沿AE,AF以及EF把这个正方形折成一个空间图形,使B,C,D三点重合,重合后的点记为H,下列说法正确的是( )
A.AG⊥平面EFH B.AH⊥平面EFH C.HF⊥平面AEH D.HG⊥平面AEF
二.填空题。(共4小题,每小题5分,共20分)
13.设复数z=1+2i,(i是虚数单位),则在复平面内,复数z2对应的点的坐标为 .
14.设复数z=+(m2+2m-15)i为实数,则实数m的值是 .
15.如图,在圆柱内有一个球,该球与圆柱的上下底面以及母线均相切,已知圆柱的底面半径为3,则圆柱的体积为 .
16.已知圆柱的轴截面是正方形,若圆柱的高与球的直径相等,则圆柱的表面积与球的表面积之比为 .
三.解答题。
17.(10分)求实数m的值或取值范围,使得复数z=m2+m-2+(m2-1)i分别满足:
(1)z是实数.
(2)z是纯虚数.
(3)z是平面中对应的点位于第二象限.
18.(12分)蒙古包是蒙古族牧民的居住一种房子,建造和搬迁都很方便,适于牧业生产和游牧生活,蒙古包古代称穹庐,如图1所示,一个普通的蒙古包可视为一个圆锥和一个圆柱的组合,如图2所示,已知该圆锥的高为2米,圆柱的高为3米,底面直径为6米.
(1)求该蒙古包的侧面积.
(2)求该蒙古包的体积.
19.(12分)已知复数z使得z+2i∈R,∈R,其中i是虚数单位.
(1)求复数z的共轭复数.
(2)若复数(z+mi)2在复平面上对应的点在第四象限,求实数m的取值范围.
20.(12分)如图,AD⊥平面ABC,CE⊥平面ABC,AD与CE不相等,AC=AD=AB=1,BC=,四棱锥B-ACED的体积为,F为BC的中点,求:
(1)CE的长度.
(2)证明:AF∥平面BDE.
(3)平面BDE∥平面BCE.
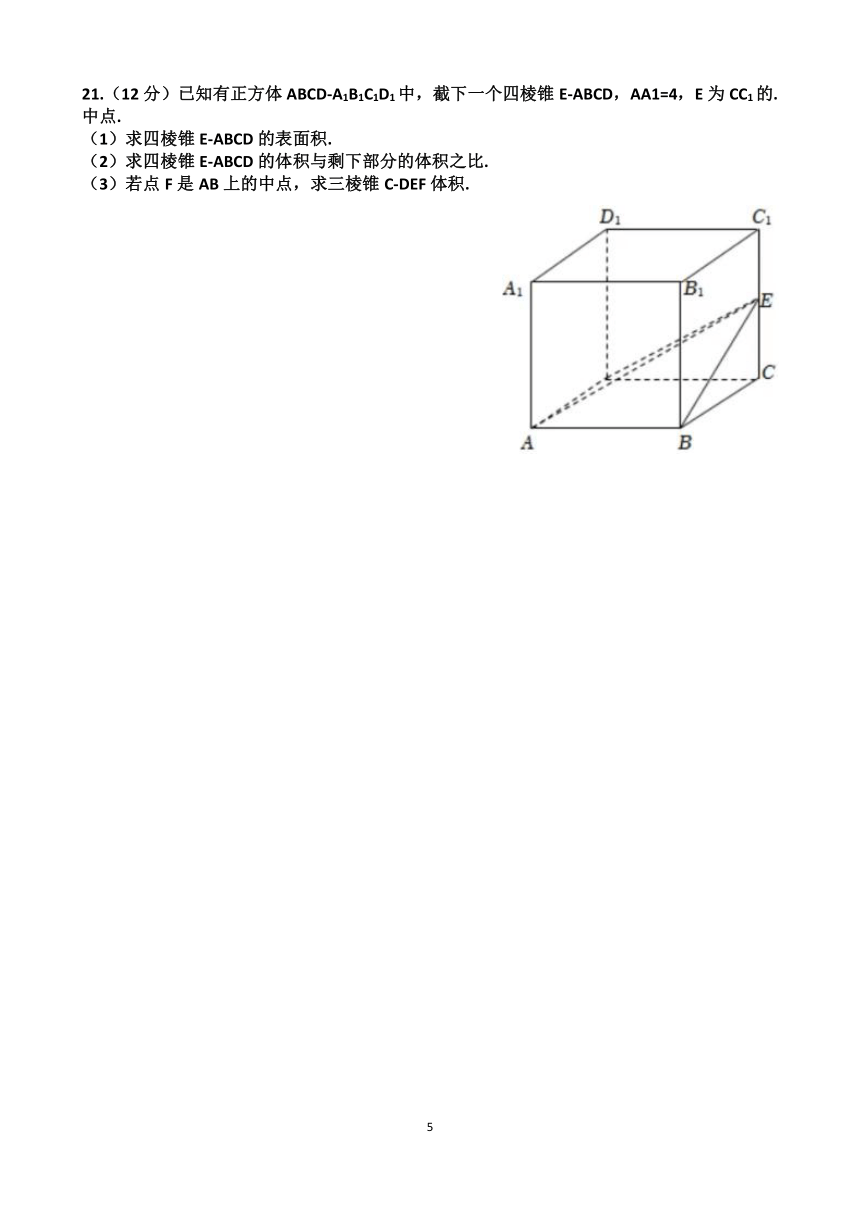
21.(12分)已知有正方体ABCD-A1B1C1D1中,截下一个四棱锥E-ABCD,AA1=4,E为CC1的.中点.
(1)求四棱锥E-ABCD的表面积.
(2)求四棱锥E-ABCD的体积与剩下部分的体积之比.
(3)若点F是AB上的中点,求三棱锥C-DEF体积.
22.(12分)已知点O是正方形ABCD两对角线的交点,DE⊥平面ABCD,BF⊥平面ABCD,且AB=BF=2DE.
(1)求证:EO⊥平面AFC.
(2)试问在线段DF(不含端点)上是否存在一点R,使得CR∥平面ABF,若存在,请指出R的位置,若不存在,说明理由.
答案解析
一.单选题。(共8小题,每小题5分,共40分)
1.已知(1+i)z=3-i,其中i为虚数单位,则=( B )
A.5 B. C.2 D.
2.已知复数z=(i为虚数单位),则z的共轭复数在复平面内对应的点位于( D )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.如图,正方形O’A’B’C’的边长为1,它是一个水平放置的平面图形的直观图,则原图形的周长是( B )
A.4 B.6 C.8 D.2+2
(第3题图) (第4题图)
4.如图,在长方体ABCD-A1B1C1D1中,AB=BC=2,AA1=1,则AC1与平面A1B1C1D1所成角的正弦值为( D )
A. B. C. D.
5.设b,c表示两条直线,α,β表示两个平面,下列命题正确的是( D )
A.若b∥α,cα,则b∥c B.若bα,b∥c,则cα
C.若c∥α,α⊥β,则c⊥β D.若c∥α,c⊥β,则α⊥β
6.已知圆锥的顶点为P,底面圆心为O,若过直线OP的平面截圆锥所得的截面是面积为4的等腰直角三角形,则该圆锥的侧面积为( A )
A.4π B.2π C.4π D.(4+4)π
7.已知圆锥的母线长为10,侧面展开图的圆心角为,则该圆锥的体积为( D )
A.π B.32π C.16π D.π
8.已知在正方体中,AD1,A1D交于点O,则( C )
A.OB⊥平面ACC1A1 B.OB⊥平面A1B1CD
C.OB∥平面CD1B1 D.OB⊥BC1
二.多选题.(共4小题,每小题5分,共20分)
9.已知复数z=3+4i,下列说法正确的是( ABD )
A.复数z的实部为3 B.复数z的共轭复数为3-4i
C.复数z的虚部为4i D.复数z的模为5
10.如图,点A,B,C,M,N是正方体的顶点或所在棱的中点,则满足MN∥平面ABC的有( AD )
A. B. C. D.
11.如图,一个圆柱盒一个圆锥的底面直径和它们的高都与一个球的直径2R相等,下列结论正确的是( BCD )
A.圆锥的侧面积为2πR2 B.圆柱与球的表面积比为
C.圆柱的侧面积与球的表面积相等 D.圆柱与球的体积比为
(第11题图) (第12题图)
12.如图,在正方形ABCD中,E、F分别是BC,CD的中点,G是EF的中点,现在沿AE,AF以及EF把这个正方形折成一个空间图形,使B,C,D三点重合,重合后的点记为H,下列说法正确的是( BCD )
A.AG⊥平面EFH B.AH⊥平面EFH C.HF⊥平面AEH D.HG⊥平面AEF
二.填空题。(共4小题,每小题5分,共20分)
13.设复数z=1+2i,(i是虚数单位),则在复平面内,复数z2对应的点的坐标为 (﹣3,4) .
14.设复数z=+(m2+2m-15)i为实数,则实数m的值是 3 .
15.如图,在圆柱内有一个球,该球与圆柱的上下底面以及母线均相切,已知圆柱的底面半径为3,则圆柱的体积为 54π .
16.已知圆柱的轴截面是正方形,若圆柱的高与球的直径相等,则圆柱的表面积与球的表面积之比为 .
三.解答题。
17.(10分)求实数m的值或取值范围,使得复数z=m2+m-2+(m2-1)i分别满足:
(1)z是实数.
(2)z是纯虚数.
(3)z是平面中对应的点位于第二象限.
(1)由题意知:
m2-1=0
m=±1
(2)由题意知:
解得m=﹣2
(3)由题意知:
解得m的取值范围是(﹣2,﹣1)
18.(12分)蒙古包是蒙古族牧民的居住一种房子,建造和搬迁都很方便,适于牧业生产和游牧生活,蒙古包古代称穹庐,如图1所示,一个普通的蒙古包可视为一个圆锥和一个圆柱的组合,如图2所示,已知该圆锥的高为2米,圆柱的高为3米,底面直径为6米.
(1)求该蒙古包的侧面积.
(2)求该蒙古包的体积.
(1)已知BC=DE=3m,AE=2m,BE=3m,
∴AD==m
圆柱的侧面积:2π×BC×BE=2π×3×3=18π平方米
圆锥的侧面积:×2π×DE×AD=×2π×3×=3π
蒙古包侧面积:(3π+18π)平方米
圆锥的体积:V=Sh=×π×32×2=6π立方米
圆柱的体积V=Sh=π×32×3=27π立方米
蒙古包体积:6π+27π=33π立方米
19.(12分)已知复数z使得z+2i∈R,∈R,其中i是虚数单位.
(1)求复数z的共轭复数.
(2)若复数(z+mi)2在复平面上对应的点在第四象限,求实数m的取值范围.
(1)设z=a+bi
∴z+2i=a+(b+2)i∈R
∴b=﹣2
∴ ==+i∈R
∴=0
解得x=4
∴z=4-2i
∴=4+2i
(2)∵m为实数,
(z+mi)2=(12+4m-m2)+8(m-2)i
∴
解得﹣2<m<2
∴m的取值范围是(﹣2,2)
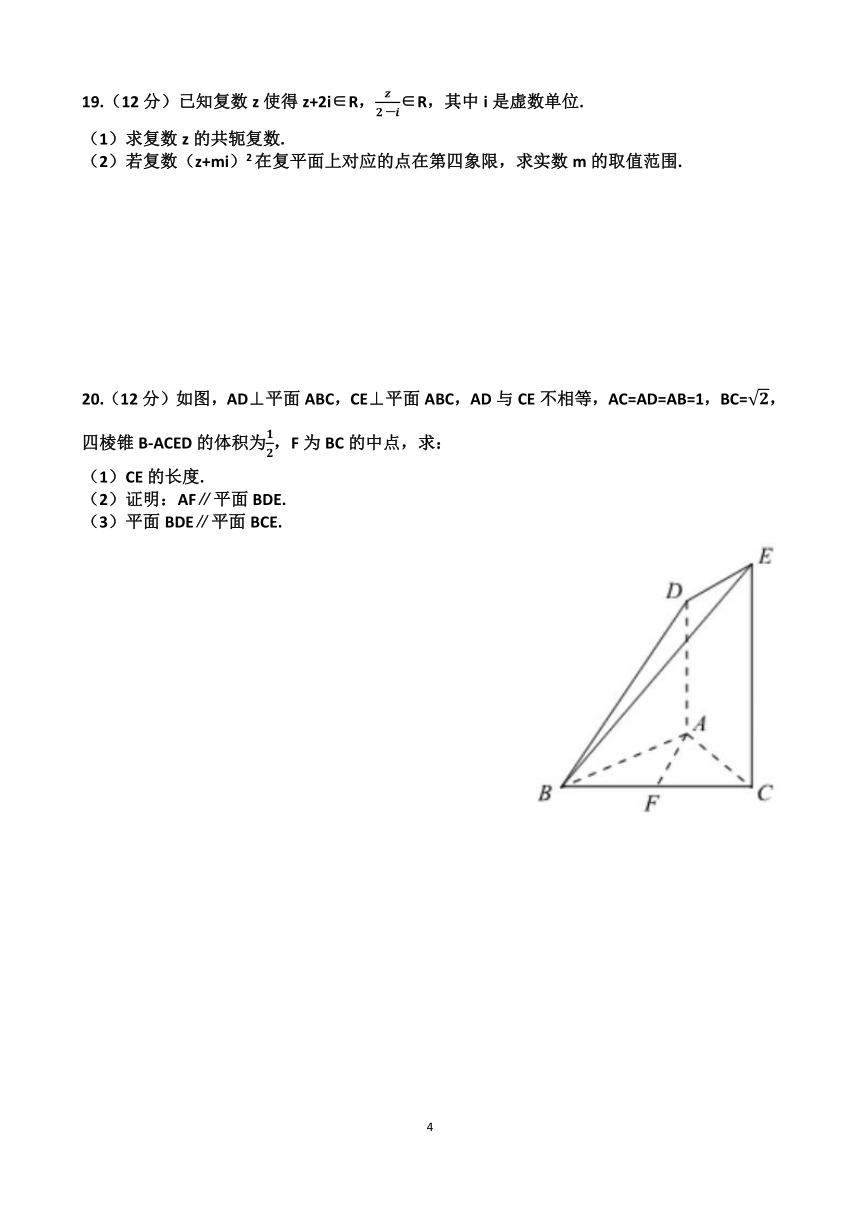
20.(12分)如图,AD⊥平面ABC,CE⊥平面ABC,AD与CE不相等,AC=AD=AB=1,BC=,四棱锥B-ACED的体积为,F为BC的中点,求:
(1)CE的长度.
(2)证明:AF∥平面BDE.
(3)平面BDE∥平面BCE.
(1)∵四边形ABCD为梯形,且平面ABC⊥∥ACED
∵BC2=AC2+AB2
∴AB⊥AC
∵平面ABC∩平面ACED=AC
∴AB⊥平面ACED
VB-ACED=×(AD+CE)×AC×AB=××(1+CE)×1×1=
∴CE=2
(2)取BE的中点G,连接GF,GD,则GF为三角形BCE的中位线。
∴GF∥EC∥DA GF=CE=DA
∴四边形GFAD为平行四边形,
∴AF∥GD
GD平面BDE,AF 平面BDE
∴AF∥平面BDE
(3)∵AB=AC,F为BC的中点
∴AF⊥BC
∵GF⊥AF,BC∩GF=F,
∴AF⊥平面BCE
∴平面BDE∥平面BCE
21.(12分)已知有正方体ABCD-A1B1C1D1中,截下一个四棱锥E-ABCD,AA1=4,E为CC1的.中点.
(1)求四棱锥E-ABCD的表面积.
(2)求四棱锥E-ABCD的体积与剩下部分的体积之比.
(3)若点F是AB上的中点,求三棱锥C-DEF体积.
(1)四棱锥的表面是由正方形ABCD和四个直角三角形围成.
△ABE和△ADE全等,△BCE和△DCE全等.
SABCD=22=4 S△BCE=×2×1=1
BE==
S△ABE=×2×=
∴S=4+2×1+2×=6+2
(2)∵EC为四棱柱E-ABCD的高,且EC=1
∴V=×SABCD×EC=×4×1=
正方体体积为23=8
VE-ABCD:V1=:8=1:6
∴VE-ABCD:V剩余=1:5
(3)S△CDF=S△ABCD=2,其中CE⊥平面ABCD
∴VC-DEF=×2×1=
22.(12分)已知点O是正方形ABCD两对角线的交点,DE⊥平面ABCD,BF⊥平面ABCD,且AB=BF=2DE.
(1)求证:EO⊥平面AFC.
(2)试问在线段DF(不含端点)上是否存在一点R,使得CR∥平面ABF,若存在,请指出R的位置,若不存在,说明理由.
连接FO,设AB=BF=2DE=2a
则DO=OB=a
∴OE=a,FO=a,EF=3a,在△EOF中,由EO2+FO2=EF2,
∴EO⊥OF
又DE⊥平面ABCD,
∴DE⊥AC,而BD⊥AC
∴AC⊥平面DOE,故AC⊥EO
∴EO⊥平面AFC
(2)找不到这样的R,使得CR⊥平面ABF。
(满分150分 时间:120分钟)
一.单选题。(共8小题,每小题5分,共40分)
1.已知(1+i)z=3-i,其中i为虚数单位,则=( )
A.5 B. C.2 D.
2.已知复数z=(i为虚数单位),则z的共轭复数在复平面内对应的点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.如图,正方形O’A’B’C’的边长为1,它是一个水平放置的平面图形的直观图,则原图形的周长是( )
A.4 B.6 C.8 D.2+2
(第3题图) (第4题图)
4.如图,在长方体ABCD-A1B1C1D1中,AB=BC=2,AA1=1,则AC1与平面A1B1C1D1所成角的正弦值为( )
A. B. C. D.
5.设b,c表示两条直线,α,β表示两个平面,下列命题正确的是( )
A.若b∥α,cα,则b∥c B.若bα,b∥c,则cα
C.若c∥α,α⊥β,则c⊥β D.若c∥α,c⊥β,则α⊥β
6.已知圆锥的顶点为P,底面圆心为O,若过直线OP的平面截圆锥所得的截面是面积为4的等腰直角三角形,则该圆锥的侧面积为( )
A.4π B.2π C.4π D.(4+4)π
7.已知圆锥的母线长为10,侧面展开图的圆心角为,则该圆锥的体积为( )
A.π B.32π C.16π D.π
8.已知在正方体中,AD1,A1D交于点O,则( )
A.OB⊥平面ACC1A1 B.OB⊥平面A1B1CD
C.OB∥平面CD1B1 D.OB⊥BC1
二.多选题.(共4小题,每小题5分,共20分)
9.已知复数z=3+4i,下列说法正确的是( )
A.复数z的实部为3 B.复数z的共轭复数为3-4i
C.复数z的虚部为4i D.复数z的模为5
10.如图,点A,B,C,M,N是正方体的顶点或所在棱的中点,则满足MN∥平面ABC的有( )
A. B. C. D.
11.如图,一个圆柱盒一个圆锥的底面直径和它们的高都与一个球的直径2R相等,下列结论正确的是( )
A.圆锥的侧面积为2πR2 B.圆柱与球的表面积比为
C.圆柱的侧面积与球的表面积相等 D.圆柱与球的体积比为
(第11题图) (第12题图)
12.如图,在正方形ABCD中,E、F分别是BC,CD的中点,G是EF的中点,现在沿AE,AF以及EF把这个正方形折成一个空间图形,使B,C,D三点重合,重合后的点记为H,下列说法正确的是( )
A.AG⊥平面EFH B.AH⊥平面EFH C.HF⊥平面AEH D.HG⊥平面AEF
二.填空题。(共4小题,每小题5分,共20分)
13.设复数z=1+2i,(i是虚数单位),则在复平面内,复数z2对应的点的坐标为 .
14.设复数z=+(m2+2m-15)i为实数,则实数m的值是 .
15.如图,在圆柱内有一个球,该球与圆柱的上下底面以及母线均相切,已知圆柱的底面半径为3,则圆柱的体积为 .
16.已知圆柱的轴截面是正方形,若圆柱的高与球的直径相等,则圆柱的表面积与球的表面积之比为 .
三.解答题。
17.(10分)求实数m的值或取值范围,使得复数z=m2+m-2+(m2-1)i分别满足:
(1)z是实数.
(2)z是纯虚数.
(3)z是平面中对应的点位于第二象限.
18.(12分)蒙古包是蒙古族牧民的居住一种房子,建造和搬迁都很方便,适于牧业生产和游牧生活,蒙古包古代称穹庐,如图1所示,一个普通的蒙古包可视为一个圆锥和一个圆柱的组合,如图2所示,已知该圆锥的高为2米,圆柱的高为3米,底面直径为6米.
(1)求该蒙古包的侧面积.
(2)求该蒙古包的体积.
19.(12分)已知复数z使得z+2i∈R,∈R,其中i是虚数单位.
(1)求复数z的共轭复数.
(2)若复数(z+mi)2在复平面上对应的点在第四象限,求实数m的取值范围.
20.(12分)如图,AD⊥平面ABC,CE⊥平面ABC,AD与CE不相等,AC=AD=AB=1,BC=,四棱锥B-ACED的体积为,F为BC的中点,求:
(1)CE的长度.
(2)证明:AF∥平面BDE.
(3)平面BDE∥平面BCE.
21.(12分)已知有正方体ABCD-A1B1C1D1中,截下一个四棱锥E-ABCD,AA1=4,E为CC1的.中点.
(1)求四棱锥E-ABCD的表面积.
(2)求四棱锥E-ABCD的体积与剩下部分的体积之比.
(3)若点F是AB上的中点,求三棱锥C-DEF体积.
22.(12分)已知点O是正方形ABCD两对角线的交点,DE⊥平面ABCD,BF⊥平面ABCD,且AB=BF=2DE.
(1)求证:EO⊥平面AFC.
(2)试问在线段DF(不含端点)上是否存在一点R,使得CR∥平面ABF,若存在,请指出R的位置,若不存在,说明理由.
答案解析
一.单选题。(共8小题,每小题5分,共40分)
1.已知(1+i)z=3-i,其中i为虚数单位,则=( B )
A.5 B. C.2 D.
2.已知复数z=(i为虚数单位),则z的共轭复数在复平面内对应的点位于( D )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.如图,正方形O’A’B’C’的边长为1,它是一个水平放置的平面图形的直观图,则原图形的周长是( B )
A.4 B.6 C.8 D.2+2
(第3题图) (第4题图)
4.如图,在长方体ABCD-A1B1C1D1中,AB=BC=2,AA1=1,则AC1与平面A1B1C1D1所成角的正弦值为( D )
A. B. C. D.
5.设b,c表示两条直线,α,β表示两个平面,下列命题正确的是( D )
A.若b∥α,cα,则b∥c B.若bα,b∥c,则cα
C.若c∥α,α⊥β,则c⊥β D.若c∥α,c⊥β,则α⊥β
6.已知圆锥的顶点为P,底面圆心为O,若过直线OP的平面截圆锥所得的截面是面积为4的等腰直角三角形,则该圆锥的侧面积为( A )
A.4π B.2π C.4π D.(4+4)π
7.已知圆锥的母线长为10,侧面展开图的圆心角为,则该圆锥的体积为( D )
A.π B.32π C.16π D.π
8.已知在正方体中,AD1,A1D交于点O,则( C )
A.OB⊥平面ACC1A1 B.OB⊥平面A1B1CD
C.OB∥平面CD1B1 D.OB⊥BC1
二.多选题.(共4小题,每小题5分,共20分)
9.已知复数z=3+4i,下列说法正确的是( ABD )
A.复数z的实部为3 B.复数z的共轭复数为3-4i
C.复数z的虚部为4i D.复数z的模为5
10.如图,点A,B,C,M,N是正方体的顶点或所在棱的中点,则满足MN∥平面ABC的有( AD )
A. B. C. D.
11.如图,一个圆柱盒一个圆锥的底面直径和它们的高都与一个球的直径2R相等,下列结论正确的是( BCD )
A.圆锥的侧面积为2πR2 B.圆柱与球的表面积比为
C.圆柱的侧面积与球的表面积相等 D.圆柱与球的体积比为
(第11题图) (第12题图)
12.如图,在正方形ABCD中,E、F分别是BC,CD的中点,G是EF的中点,现在沿AE,AF以及EF把这个正方形折成一个空间图形,使B,C,D三点重合,重合后的点记为H,下列说法正确的是( BCD )
A.AG⊥平面EFH B.AH⊥平面EFH C.HF⊥平面AEH D.HG⊥平面AEF
二.填空题。(共4小题,每小题5分,共20分)
13.设复数z=1+2i,(i是虚数单位),则在复平面内,复数z2对应的点的坐标为 (﹣3,4) .
14.设复数z=+(m2+2m-15)i为实数,则实数m的值是 3 .
15.如图,在圆柱内有一个球,该球与圆柱的上下底面以及母线均相切,已知圆柱的底面半径为3,则圆柱的体积为 54π .
16.已知圆柱的轴截面是正方形,若圆柱的高与球的直径相等,则圆柱的表面积与球的表面积之比为 .
三.解答题。
17.(10分)求实数m的值或取值范围,使得复数z=m2+m-2+(m2-1)i分别满足:
(1)z是实数.
(2)z是纯虚数.
(3)z是平面中对应的点位于第二象限.
(1)由题意知:
m2-1=0
m=±1
(2)由题意知:
解得m=﹣2
(3)由题意知:
解得m的取值范围是(﹣2,﹣1)
18.(12分)蒙古包是蒙古族牧民的居住一种房子,建造和搬迁都很方便,适于牧业生产和游牧生活,蒙古包古代称穹庐,如图1所示,一个普通的蒙古包可视为一个圆锥和一个圆柱的组合,如图2所示,已知该圆锥的高为2米,圆柱的高为3米,底面直径为6米.
(1)求该蒙古包的侧面积.
(2)求该蒙古包的体积.
(1)已知BC=DE=3m,AE=2m,BE=3m,
∴AD==m
圆柱的侧面积:2π×BC×BE=2π×3×3=18π平方米
圆锥的侧面积:×2π×DE×AD=×2π×3×=3π
蒙古包侧面积:(3π+18π)平方米
圆锥的体积:V=Sh=×π×32×2=6π立方米
圆柱的体积V=Sh=π×32×3=27π立方米
蒙古包体积:6π+27π=33π立方米
19.(12分)已知复数z使得z+2i∈R,∈R,其中i是虚数单位.
(1)求复数z的共轭复数.
(2)若复数(z+mi)2在复平面上对应的点在第四象限,求实数m的取值范围.
(1)设z=a+bi
∴z+2i=a+(b+2)i∈R
∴b=﹣2
∴ ==+i∈R
∴=0
解得x=4
∴z=4-2i
∴=4+2i
(2)∵m为实数,
(z+mi)2=(12+4m-m2)+8(m-2)i
∴
解得﹣2<m<2
∴m的取值范围是(﹣2,2)
20.(12分)如图,AD⊥平面ABC,CE⊥平面ABC,AD与CE不相等,AC=AD=AB=1,BC=,四棱锥B-ACED的体积为,F为BC的中点,求:
(1)CE的长度.
(2)证明:AF∥平面BDE.
(3)平面BDE∥平面BCE.
(1)∵四边形ABCD为梯形,且平面ABC⊥∥ACED
∵BC2=AC2+AB2
∴AB⊥AC
∵平面ABC∩平面ACED=AC
∴AB⊥平面ACED
VB-ACED=×(AD+CE)×AC×AB=××(1+CE)×1×1=
∴CE=2
(2)取BE的中点G,连接GF,GD,则GF为三角形BCE的中位线。
∴GF∥EC∥DA GF=CE=DA
∴四边形GFAD为平行四边形,
∴AF∥GD
GD平面BDE,AF 平面BDE
∴AF∥平面BDE
(3)∵AB=AC,F为BC的中点
∴AF⊥BC
∵GF⊥AF,BC∩GF=F,
∴AF⊥平面BCE
∴平面BDE∥平面BCE
21.(12分)已知有正方体ABCD-A1B1C1D1中,截下一个四棱锥E-ABCD,AA1=4,E为CC1的.中点.
(1)求四棱锥E-ABCD的表面积.
(2)求四棱锥E-ABCD的体积与剩下部分的体积之比.
(3)若点F是AB上的中点,求三棱锥C-DEF体积.
(1)四棱锥的表面是由正方形ABCD和四个直角三角形围成.
△ABE和△ADE全等,△BCE和△DCE全等.
SABCD=22=4 S△BCE=×2×1=1
BE==
S△ABE=×2×=
∴S=4+2×1+2×=6+2
(2)∵EC为四棱柱E-ABCD的高,且EC=1
∴V=×SABCD×EC=×4×1=
正方体体积为23=8
VE-ABCD:V1=:8=1:6
∴VE-ABCD:V剩余=1:5
(3)S△CDF=S△ABCD=2,其中CE⊥平面ABCD
∴VC-DEF=×2×1=
22.(12分)已知点O是正方形ABCD两对角线的交点,DE⊥平面ABCD,BF⊥平面ABCD,且AB=BF=2DE.
(1)求证:EO⊥平面AFC.
(2)试问在线段DF(不含端点)上是否存在一点R,使得CR∥平面ABF,若存在,请指出R的位置,若不存在,说明理由.
连接FO,设AB=BF=2DE=2a
则DO=OB=a
∴OE=a,FO=a,EF=3a,在△EOF中,由EO2+FO2=EF2,
∴EO⊥OF
又DE⊥平面ABCD,
∴DE⊥AC,而BD⊥AC
∴AC⊥平面DOE,故AC⊥EO
∴EO⊥平面AFC
(2)找不到这样的R,使得CR⊥平面ABF。
同课章节目录
