课题学习;中点四边形[下学期]

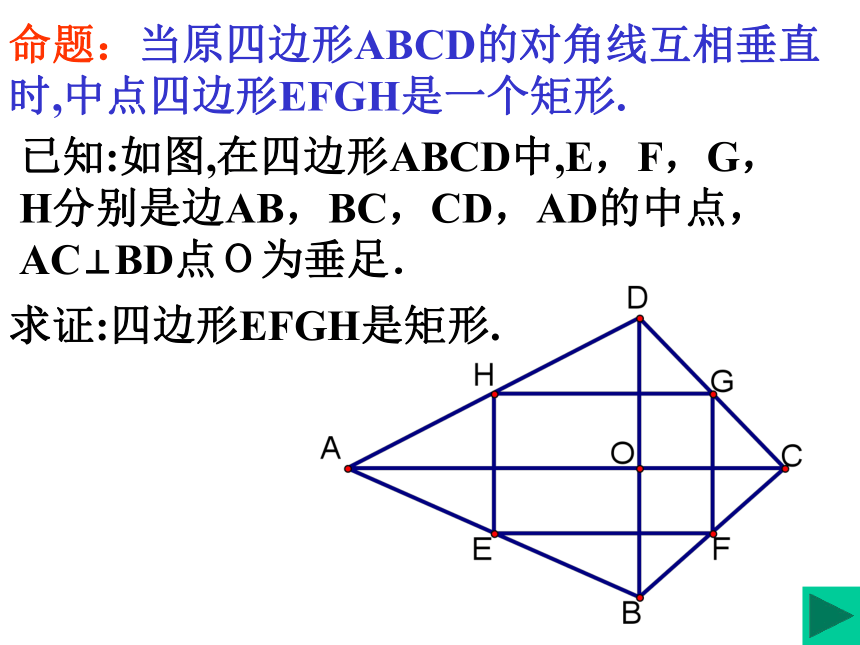
课件11张PPT。课题学习中点四边形沥海镇中　　罗飞宇观察 操作大胆 猜想推理 证明应用 拓展当原四边形ABCD的对角线互相垂直 时,中点四边形EFGH是一个矩形？猜想1:猜想2:猜想3:当原四边形ABCD的对角线相等时,中点四边形EFGH是一个菱形？当原四边形ABCD的对角线相等且互相垂直时,中点四边形EFGH是一个正方形？命题：当原四边形ABCD的对角线互相垂直时,中点四边形EFGH是一个矩形.已知:如图,在四边形ABCD中,E，F，G，H分别是边AB，BC，CD，AD的中点，AC⊥BD点Ｏ为垂足．求证:四边形EFGH是矩形.应用拓展１：１．当原四边形ＡＢＣＤ是平行四边形，中点四边形ＥＦＧＨ是平行四边形．２．当原四边形ＡＢＣＤ是矩形，中点四边形ＥＦＧＨ是菱形．３．当原四边形ＡＢＣＤ是菱形，中点四边形ＥＦＧＨ是矩形．４．当原四边形ＡＢＣＤ是正方形，中点四边形ＥＦＧＨ是正方形．５．当原四边形ＡＢＣＤ是梯形，中点四边形ＥＦＧＨ是平行四边形．６．当原四边形ＡＢＣＤ是等腰梯形，中点四边形ＥＦＧＨ是菱形．知识回顾：中点三角形概念：顺次连结三角形的各边中点所组成的三角形叫做中点三角形结论1： 结论2：结论3：结论4：中点四边形概念：顺次连结四边形的各边中点所组成的四边形叫做中点四边形。结论1：结论3：结论2：结论4：应用拓展2：五边形的面积与它中点五边形面积有没有倍数关系？
六边形。。。应用3：例 （北京实验区）如图，四边形ABCD中，AC=6，BD=8且AC⊥BD顺次连接四边形ABCD各边中点，得到四边形A1B1C1D1；再顺次连接四边形A1B1C1D1各边中点，得到四边形A2B2C2D2……如此进行下去得到四边形AnBnCnDn . （1）证明：四边形A1B1C1D1是矩形； （2）写出四边形A1B1C1D1和四边形A2B2C2D2的面积； （3）写出四边形AnBnCnDn的面积； （4）求四边形A5B5C5D5的周长. 中考命题改革亮点题目 应用拓展4：图形１图形２谢谢再见