2023年中考数学微专题复习提升测试卷——圆与正多边形(含答案)
文档属性
| 名称 | 2023年中考数学微专题复习提升测试卷——圆与正多边形(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 217.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-06 18:06:39 | ||
图片预览


文档简介
微专题复习提升测试卷——圆与正多边形
(时间:60分钟 分数:100分)
姓名: 分数:
选择题(本题共8小题,共40分)
1.(2020 黔东南州)如图,⊙O的直径CD=20,AB是⊙O的弦,AB⊥CD,垂足为M,OM:OC=3:5,则AB的长为( )
A.8 B.12 C.16 D.2
2.(2020 营口)如图,AB为⊙O的直径,点C,点D是⊙O上的两点,连接CA,CD,AD.若∠CAB=40°,则∠ADC的度数是( )
A.110° B.130° C.140° D.160°
3.(2022·四川广元)如图,AB是⊙O的直径,C、D是⊙O上的两点,若∠CAB=65°,则∠ADC的度数为( )
A.25° B.35° C.45° D.65°
4.(2020 河北)有一题目:“已知:点O为△ABC的外心,∠BOC=130°,求∠A.”嘉嘉的解答为:画△ABC以及它的外接圆O,连接OB,OC.如图,由∠BOC=2∠A=130°,得∠A=65°.而淇淇说:“嘉嘉考虑的不周全,∠A还应有另一个不同的值.”下列判断正确的是( )
A.淇淇说的对,且∠A的另一个值是115°
B.淇淇说的不对,∠A就得65°
C.嘉嘉求的结果不对,∠A应得50°
D.两人都不对,∠A应有3个不同值
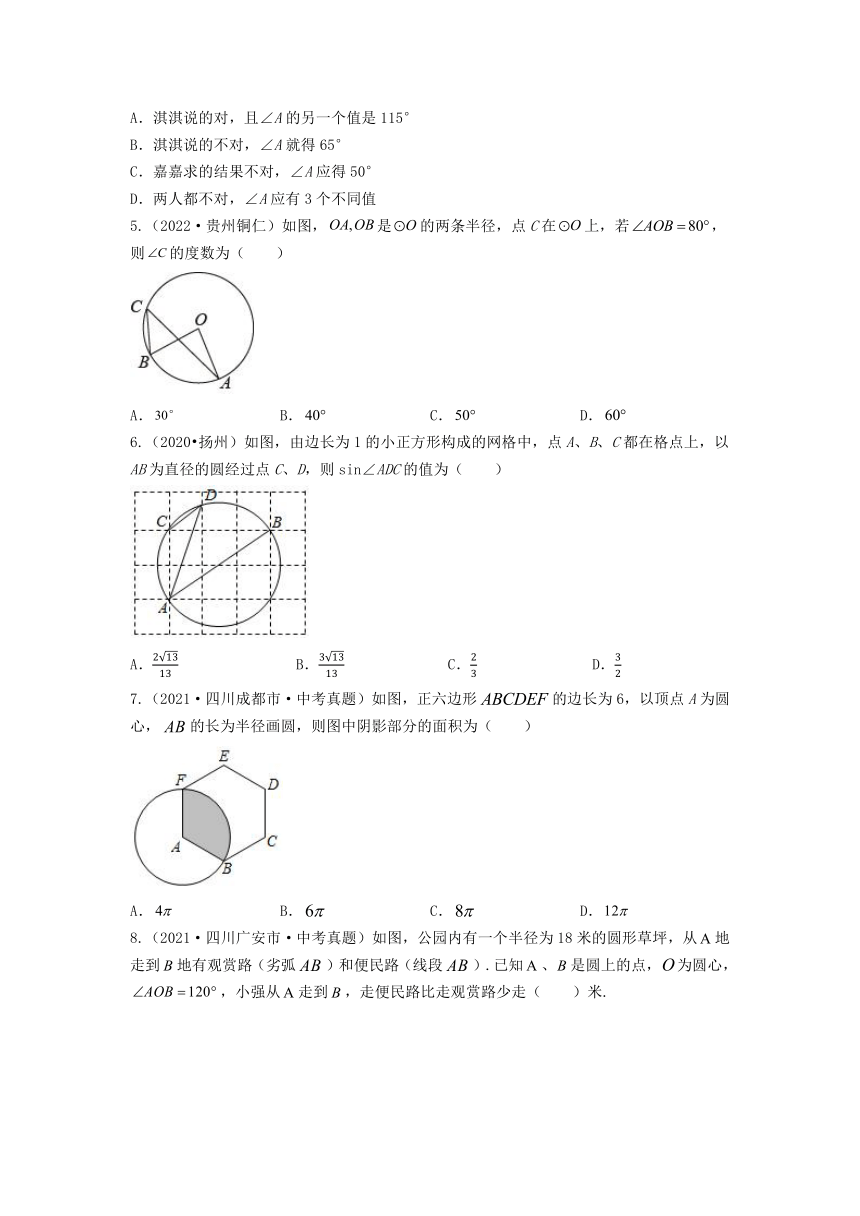
5.(2022·贵州铜仁)如图,是的两条半径,点C在上,若,则的度数为( )
A. B. C. D.
6.(2020 扬州)如图,由边长为1的小正方形构成的网格中,点A、B、C都在格点上,以AB为直径的圆经过点C、D,则sin∠ADC的值为( )
A. B. C. D.
7.(2021·四川成都市·中考真题)如图,正六边形的边长为6,以顶点A为圆心,的长为半径画圆,则图中阴影部分的面积为( )
A. B. C. D.
8.(2021·四川广安市·中考真题)如图,公园内有一个半径为18米的圆形草坪,从地走到地有观赏路(劣弧)和便民路(线段).已知、是圆上的点,为圆心,,小强从走到,走便民路比走观赏路少走( )米.
A. B. C. D.
填空题(本题共5小题,每空3分,共15分)
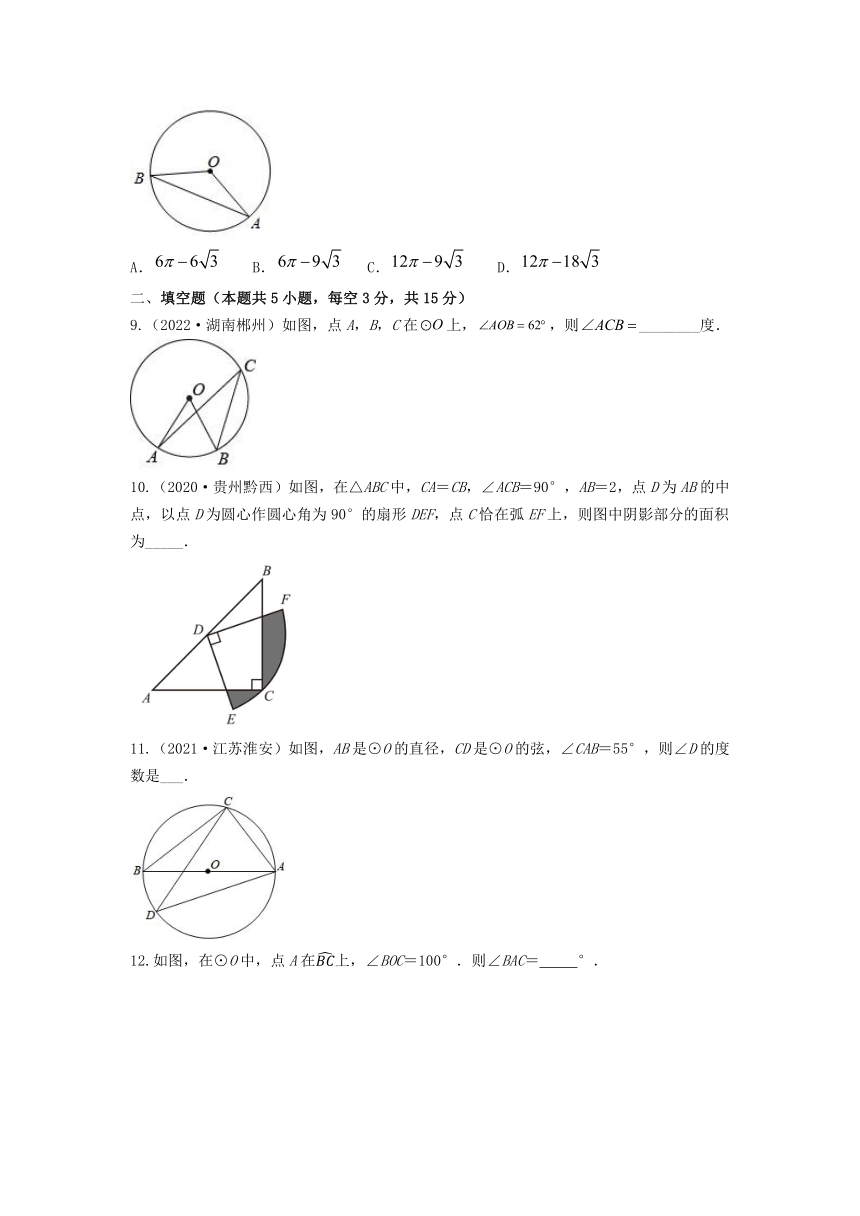
9.(2022·湖南郴州)如图,点A,B,C在上,,则________度.
10.(2020·贵州黔西)如图,在△ABC中,CA=CB,∠ACB=90°,AB=2,点D为AB的中点,以点D为圆心作圆心角为90°的扇形DEF,点C恰在弧EF上,则图中阴影部分的面积为_____.
11.(2021·江苏淮安)如图,AB是⊙O的直径,CD是⊙O的弦,∠CAB=55°,则∠D的度数是___.
12.如图,在⊙O中,点A在上,∠BOC=100°.则∠BAC= °.
13.如图,已知锐角三角形ABC内接于半径为2的⊙O,OD⊥BC于点D,∠BAC=60°,则OD= .
解答题(本题共3小题,共45分)
14.(2021·四川南充市·中考真题)如图,A,B是上两点,且,连接OB并延长到点C,使,连接AC.(1)求证:AC是的切线.(2)点D,E分别是AC,OA的中点,DE所在直线交于点F,G,,求GF的长.
15.如图,在△ABC中,BA=BC,∠ABC=90°,以AB为直径的半圆O交AC于点D,点E是上不与点B,D重合的任意一点,连接AE交BD于点F,连接BE并延长交AC于点G.
(1)求证:△ADF≌△BDG;
(2)填空:
①若AB=4,且点E是的中点,则DF的长为__________;
②取的中点H,当∠EAB的度数为__________时,四边形OBEH为菱形.
16.(2020 南京)如图,在△ABC中,AC=BC,D是AB上一点,⊙O经过点A、C、D,交BC于点E,过点D作DF∥BC,交⊙O于点F.
求证:(1)四边形DBCF是平行四边形;
(2)AF=EF.
参考答案:
1.C 2.B 3.A 4.A 5.B 6.A 7.D 8.D
9.31
10.﹣
11.35°
12.130
13.1
14.(1)证明:∵AB=OA,OA=OB∴AB=OA=OB
∴△AOB为等边三角形∴∠OAB=60°,∠OBA=60° ∵BC=OB∴BC=AB∴∠C=∠CAB
又∵∠OBA=60°=∠C+∠CAB∴∠C=∠CAB=30°
∴∠OAC=∠OAB+∠CAB=90°∴AC是⊙O的切线;
(2)∵OA=4 ∴OB=AB=BC=4 ∴OC=8 ∴AC===
∵D、E分别为AC、OA的中点, ∴OE//BC,DC=
过O作OM⊥DF于M,DN⊥OC于N 则四边形OMDN为矩形 ∴DN=OM
在Rt△CDN中,∠C=30°,∴DN=DC= ∴OM=
连接OG,∵OM⊥GF ∴GF=2MG=2==2
15.(1)∵BA=BC,∠ABC=90°,
∴∠BAC=45°,
∵AB是⊙O的直径,
∴∠ADB=∠AEB=90°,
∴∠DAF+∠BGD=∠DBG+∠BGD=90°,
∴∠DAF=∠DBG,
∵∠ABD+∠BAC=90°,
∴∠ABD=∠BAC=45°,
∴AD=BD,
∴△ADF≌△BDG.
(2)①如图2,过F作FH⊥AB于H,
∵点E是的中点,
∴∠BAE=∠DAE,
∵FD⊥AD,FH⊥AB,
∴FH=FD,
∵=sin∠ABD=sin45°=,
∴,即BF=FD,
∵AB=4,
∴BD=4cos45°=2,即BF+FD=2,( +1)FD=2,
∴FD==4-2,
故答案为:4-2.
②连接OH,EH,
∵点H是的中点,
∴OH⊥AE,
∵∠AEB=90°,
∴BE⊥AE,
∴BE∥OH,
∵四边形OBEH为菱形,
∴BE=OH=OB=AB,
∴sin∠EAB==,
∴∠EAB=30°.
故答案为:30°.
16.证明:(1)∵AC=BC,
∴∠BAC=∠B,
∵DF∥BC,
∴∠ADF=∠B,
∵∠BAC=∠CFD,
∴∠ADF=∠CFD,
∴BD∥CF,
∵DF∥BC,
∴四边形DBCF是平行四边形;
(2)连接AE,
∵∠ADF=∠B,∠ADF=∠AEF,
∴∠AEF=∠B,
∵四边形AECF是⊙O的内接四边形,
∴∠ECF+∠EAF=180°,
∵BD∥CF,
∴∠ECF+∠B=180°,
∴∠EAF=∠B,
∴∠AEF=∠EAF,
∴AE=EF.
(时间:60分钟 分数:100分)
姓名: 分数:
选择题(本题共8小题,共40分)
1.(2020 黔东南州)如图,⊙O的直径CD=20,AB是⊙O的弦,AB⊥CD,垂足为M,OM:OC=3:5,则AB的长为( )
A.8 B.12 C.16 D.2
2.(2020 营口)如图,AB为⊙O的直径,点C,点D是⊙O上的两点,连接CA,CD,AD.若∠CAB=40°,则∠ADC的度数是( )
A.110° B.130° C.140° D.160°
3.(2022·四川广元)如图,AB是⊙O的直径,C、D是⊙O上的两点,若∠CAB=65°,则∠ADC的度数为( )
A.25° B.35° C.45° D.65°
4.(2020 河北)有一题目:“已知:点O为△ABC的外心,∠BOC=130°,求∠A.”嘉嘉的解答为:画△ABC以及它的外接圆O,连接OB,OC.如图,由∠BOC=2∠A=130°,得∠A=65°.而淇淇说:“嘉嘉考虑的不周全,∠A还应有另一个不同的值.”下列判断正确的是( )
A.淇淇说的对,且∠A的另一个值是115°
B.淇淇说的不对,∠A就得65°
C.嘉嘉求的结果不对,∠A应得50°
D.两人都不对,∠A应有3个不同值
5.(2022·贵州铜仁)如图,是的两条半径,点C在上,若,则的度数为( )
A. B. C. D.
6.(2020 扬州)如图,由边长为1的小正方形构成的网格中,点A、B、C都在格点上,以AB为直径的圆经过点C、D,则sin∠ADC的值为( )
A. B. C. D.
7.(2021·四川成都市·中考真题)如图,正六边形的边长为6,以顶点A为圆心,的长为半径画圆,则图中阴影部分的面积为( )
A. B. C. D.
8.(2021·四川广安市·中考真题)如图,公园内有一个半径为18米的圆形草坪,从地走到地有观赏路(劣弧)和便民路(线段).已知、是圆上的点,为圆心,,小强从走到,走便民路比走观赏路少走( )米.
A. B. C. D.
填空题(本题共5小题,每空3分,共15分)
9.(2022·湖南郴州)如图,点A,B,C在上,,则________度.
10.(2020·贵州黔西)如图,在△ABC中,CA=CB,∠ACB=90°,AB=2,点D为AB的中点,以点D为圆心作圆心角为90°的扇形DEF,点C恰在弧EF上,则图中阴影部分的面积为_____.
11.(2021·江苏淮安)如图,AB是⊙O的直径,CD是⊙O的弦,∠CAB=55°,则∠D的度数是___.
12.如图,在⊙O中,点A在上,∠BOC=100°.则∠BAC= °.
13.如图,已知锐角三角形ABC内接于半径为2的⊙O,OD⊥BC于点D,∠BAC=60°,则OD= .
解答题(本题共3小题,共45分)
14.(2021·四川南充市·中考真题)如图,A,B是上两点,且,连接OB并延长到点C,使,连接AC.(1)求证:AC是的切线.(2)点D,E分别是AC,OA的中点,DE所在直线交于点F,G,,求GF的长.
15.如图,在△ABC中,BA=BC,∠ABC=90°,以AB为直径的半圆O交AC于点D,点E是上不与点B,D重合的任意一点,连接AE交BD于点F,连接BE并延长交AC于点G.
(1)求证:△ADF≌△BDG;
(2)填空:
①若AB=4,且点E是的中点,则DF的长为__________;
②取的中点H,当∠EAB的度数为__________时,四边形OBEH为菱形.
16.(2020 南京)如图,在△ABC中,AC=BC,D是AB上一点,⊙O经过点A、C、D,交BC于点E,过点D作DF∥BC,交⊙O于点F.
求证:(1)四边形DBCF是平行四边形;
(2)AF=EF.
参考答案:
1.C 2.B 3.A 4.A 5.B 6.A 7.D 8.D
9.31
10.﹣
11.35°
12.130
13.1
14.(1)证明:∵AB=OA,OA=OB∴AB=OA=OB
∴△AOB为等边三角形∴∠OAB=60°,∠OBA=60° ∵BC=OB∴BC=AB∴∠C=∠CAB
又∵∠OBA=60°=∠C+∠CAB∴∠C=∠CAB=30°
∴∠OAC=∠OAB+∠CAB=90°∴AC是⊙O的切线;
(2)∵OA=4 ∴OB=AB=BC=4 ∴OC=8 ∴AC===
∵D、E分别为AC、OA的中点, ∴OE//BC,DC=
过O作OM⊥DF于M,DN⊥OC于N 则四边形OMDN为矩形 ∴DN=OM
在Rt△CDN中,∠C=30°,∴DN=DC= ∴OM=
连接OG,∵OM⊥GF ∴GF=2MG=2==2
15.(1)∵BA=BC,∠ABC=90°,
∴∠BAC=45°,
∵AB是⊙O的直径,
∴∠ADB=∠AEB=90°,
∴∠DAF+∠BGD=∠DBG+∠BGD=90°,
∴∠DAF=∠DBG,
∵∠ABD+∠BAC=90°,
∴∠ABD=∠BAC=45°,
∴AD=BD,
∴△ADF≌△BDG.
(2)①如图2,过F作FH⊥AB于H,
∵点E是的中点,
∴∠BAE=∠DAE,
∵FD⊥AD,FH⊥AB,
∴FH=FD,
∵=sin∠ABD=sin45°=,
∴,即BF=FD,
∵AB=4,
∴BD=4cos45°=2,即BF+FD=2,( +1)FD=2,
∴FD==4-2,
故答案为:4-2.
②连接OH,EH,
∵点H是的中点,
∴OH⊥AE,
∵∠AEB=90°,
∴BE⊥AE,
∴BE∥OH,
∵四边形OBEH为菱形,
∴BE=OH=OB=AB,
∴sin∠EAB==,
∴∠EAB=30°.
故答案为:30°.
16.证明:(1)∵AC=BC,
∴∠BAC=∠B,
∵DF∥BC,
∴∠ADF=∠B,
∵∠BAC=∠CFD,
∴∠ADF=∠CFD,
∴BD∥CF,
∵DF∥BC,
∴四边形DBCF是平行四边形;
(2)连接AE,
∵∠ADF=∠B,∠ADF=∠AEF,
∴∠AEF=∠B,
∵四边形AECF是⊙O的内接四边形,
∴∠ECF+∠EAF=180°,
∵BD∥CF,
∴∠ECF+∠B=180°,
∴∠EAF=∠B,
∴∠AEF=∠EAF,
∴AE=EF.
同课章节目录
