2023年中考数学微专题复习提升测试卷——相似三角形(含答案)
文档属性
| 名称 | 2023年中考数学微专题复习提升测试卷——相似三角形(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 251.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-06 18:21:05 | ||
图片预览

文档简介
微专题复习提升测试卷——相似三角形
(时间:60分钟 分数:100分)
姓名: 分数:
选择题(本题共8小题,共40分)
1.(2022·甘肃兰州)已知,,若,则( )
A.4 B.6 C.8 D.16
2.(2020 嘉兴)如图,在直角坐标系中,△OAB的顶点为O(0,0),A(4,3),B(3,0).以点O为位似中心,在第三象限内作与△OAB的位似比为的位似图形△OCD,则点C坐标( )
A.(﹣1,﹣1) B.(,﹣1) C.(﹣1,) D.(﹣2,﹣1)
3.(2021·四川遂宁市·中考真题)如图,在△ABC中,点D、E分别是AB、AC的中点,若△ADE的面积是3cm2,则四边形BDEC的面积为( )
A.12cm2 B.9cm2 C.6cm2 D.3cm2
4.(2020·广西贵港市·中考真题)如图,在中,点在边上,若,,且,则线段的长为( )
A.2 B. C.3 D.
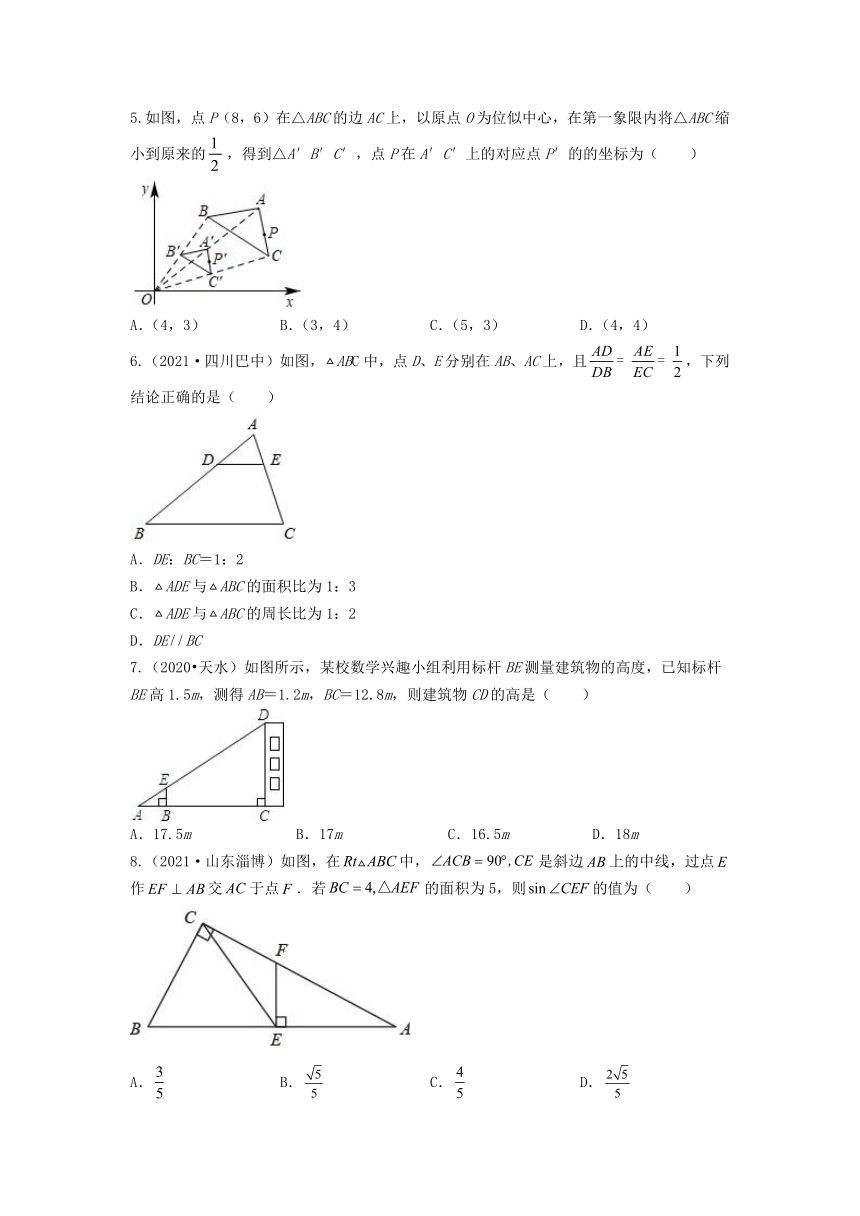
5.如图,点P(8,6)在△ABC的边AC上,以原点O为位似中心,在第一象限内将△ABC缩小到原来的,得到△A′B′C′,点P在A′C′上的对应点P′的的坐标为( )
A.(4,3) B.(3,4) C.(5,3) D.(4,4)
6.(2021·四川巴中)如图,ABC中,点D、E分别在AB、AC上,且,下列结论正确的是( )
A.DE:BC=1:2
B.ADE与ABC的面积比为1:3
C.ADE与ABC的周长比为1:2
D.DEBC
7.(2020 天水)如图所示,某校数学兴趣小组利用标杆BE测量建筑物的高度,已知标杆BE高1.5m,测得AB=1.2m,BC=12.8m,则建筑物CD的高是( )
A.17.5m B.17m C.16.5m D.18m
8.(2021·山东淄博)如图,在中,是斜边上的中线,过点作交于点.若的面积为5,则的值为( )
A. B. C. D.
填空题(本题共4小题,每空3分,共15分)
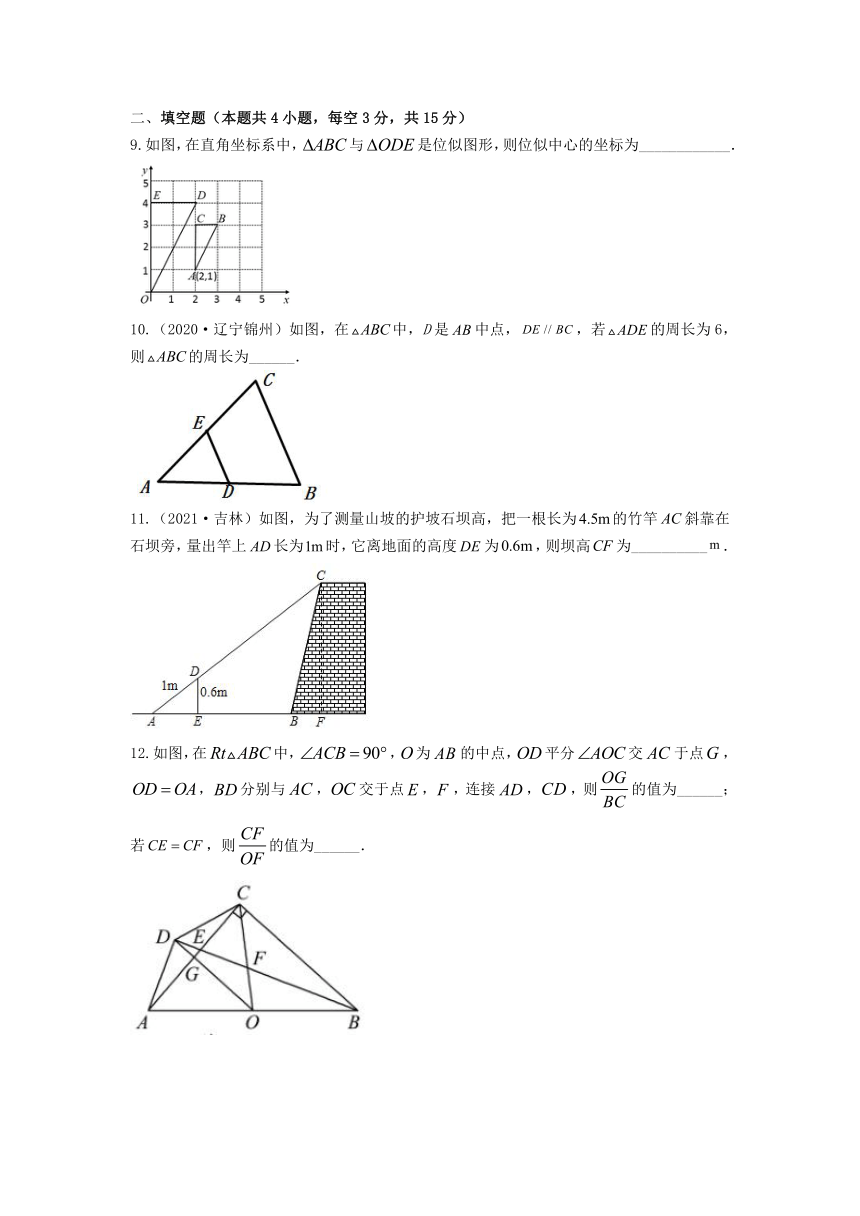
9.如图,在直角坐标系中,与是位似图形,则位似中心的坐标为____________.
10.(2020·辽宁锦州)如图,在中,D是中点,,若的周长为6,则的周长为______.
11.(2021·吉林)如图,为了测量山坡的护坡石坝高,把一根长为的竹竿斜靠在石坝旁,量出竿上长为时,它离地面的高度为,则坝高为__________.
12.如图,在中,,为的中点,平分交于点,,分别与,交于点,,连接,,则的值为______;若,则的值为______.
解答题(本题共3小题,共45分)
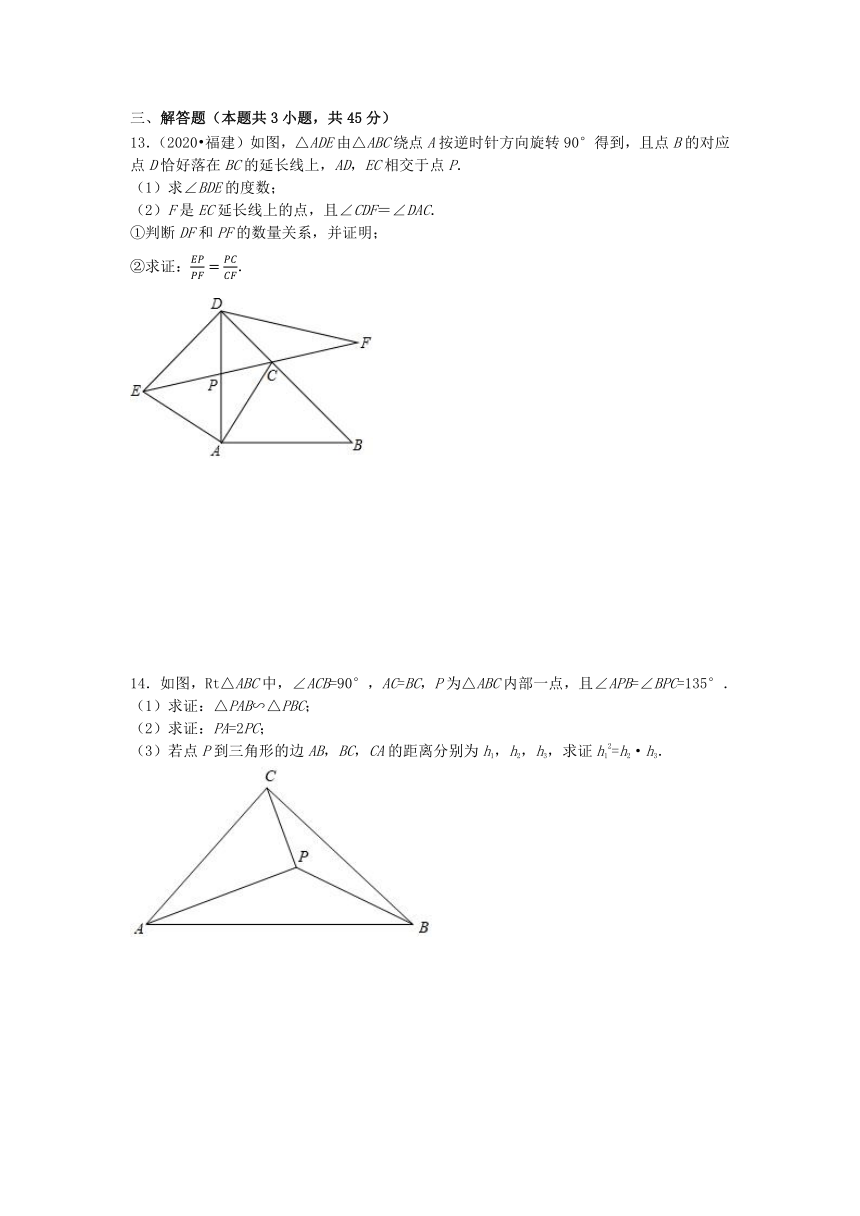
13.(2020 福建)如图,△ADE由△ABC绕点A按逆时针方向旋转90°得到,且点B的对应点D恰好落在BC的延长线上,AD,EC相交于点P.
(1)求∠BDE的度数;
(2)F是EC延长线上的点,且∠CDF=∠DAC.
①判断DF和PF的数量关系,并证明;
②求证:.
14.如图,Rt△ABC中,∠ACB=90°,AC=BC,P为△ABC内部一点,且∠APB=∠BPC=135°.
(1)求证:△PAB∽△PBC;
(2)求证:PA=2PC;
(3)若点P到三角形的边AB,BC,CA的距离分别为h1,h2,h3,求证h12=h2·h3.
15.(2022·四川自贡)如图,用四根木条钉成矩形框,把边固定在地面上,向右推动矩形框,矩形框的形状会发生改变(四边形具有不稳定性).
(1)通过观察分析,我们发现图中线段存在等量关系,如线段由旋转得到,所以.我们还可以得到= , = ;
(2)进一步观察,我们还会发现∥,请证明这一结论;
(3)已知,若 恰好经过原矩形边的中点 ,求与之间的距离.
参考答案:
1.A 2.B 3.B 4.B 5.A 6.D 7.A 8.A
9.
10.12
11.2.7
12.
13.(1)∵△ADE由△ABC绕点A按逆时针方向旋转90°得到,
∴AB=AD,∠BAD=90°,△ABC≌△ADE,
在Rt△ABD中,∠B=∠ADB=45°,
∴∠ADE=∠B=45°,
∴∠BDE=∠ADB+∠ADE=90°.
(2)①DF=PF.
证明:由旋转的性质可知,AC=AE,∠CAE=90°,
在Rt△ACE中,∠ACE=∠AEC=45°,
∵∠CDF=∠CAD,∠ACE=∠ADB=45°,
∴∠ADB+∠CDF=∠ACE+∠CAD,
即∠FPD=∠FDP,
∴DF=PF.
②证明:过点P作PH∥ED交DF于点H,
∴∠HPF=∠DEP,,
∵∠DPF=∠ADE+∠DEP=45°+∠DEP,
∠DPF=∠ACE+∠DAC=45°+∠DAC,
∴∠DEP=∠DAC,
又∵∠CDF=∠DAC,
∴∠DEP=∠CDF,
∴∠HPF=∠CDF,
又∵FD=FP,∠F=∠F,
∴△HPF≌△CDF(ASA),
∴HF=CF,
∴DH=PC,
又∵,
∴.
14.(1)∵∠ACB=90°,AB=BC,
∴∠ABC=45°=∠PBA+∠PBC,
又∠APB=135°,∴∠PAB+∠PBA=45°,
∴∠PBC=∠PAB,
又∵∠APB=∠BPC=135°,
∴△PAB∽△PBC.
(2)∵△PAB∽△PBC,∴,
在Rt△ABC中,AB=AC,∴,
∴,
∴PA=2PC.
(3)如图,过点P作PD⊥BC,PE⊥AC交BC、AC于点D,E,
∴PF=h1,PD=h2,PE=h3,
∵∠CPB+∠APB=135°+135°=270°,
∴∠APC=90°,
∴∠EAP+∠ACP=90°,
又∵∠ACB=∠ACP+∠PCD=90°,
∴∠EAP=∠PCD,
∴Rt△AEP∽Rt△CDP,
∴,即,∴h3=2h2,
∵△PAB∽△PBC,∴,
∴,
∴.即h12=h2·h3
15.(1)
解:∵ 把边固定在地面上,向右推动矩形框,矩形框的形状会发生改变(四边形具有不稳定性).
∴由旋转的性质可知矩形ABCD的各边的长度没有改变,
∴AB=BE,EF=AD,CF=CD,
故答案为:CD,AD;
(2)
解:∵四边形ABCD是矩形,
∴ADBC,AB=CD,AD=BC,
∵AB=BE,EF=AD,CF=CD,
∴BE=CF,EF=BC,
∴四边形BEFC是平行四边形,
∴EFBC,
∴EFAD;
(3)
解:如图,过点E作EG⊥BC于点G,
∵DC=AB=BE=80cm,点H是CD的中点,
∴ CH=DH=40cm,
在Rt△BHC中,∠BCH=90°,
BH=(cm),
∵ EG⊥BC,
∴∠EGB=∠BCH=90°,
∴CHEG,
∴ △BCH∽△BGE,
∴,
∴,
∴EG=64,
∵ EFBC,
∴EF与BC之间的距离为64cm.
(时间:60分钟 分数:100分)
姓名: 分数:
选择题(本题共8小题,共40分)
1.(2022·甘肃兰州)已知,,若,则( )
A.4 B.6 C.8 D.16
2.(2020 嘉兴)如图,在直角坐标系中,△OAB的顶点为O(0,0),A(4,3),B(3,0).以点O为位似中心,在第三象限内作与△OAB的位似比为的位似图形△OCD,则点C坐标( )
A.(﹣1,﹣1) B.(,﹣1) C.(﹣1,) D.(﹣2,﹣1)
3.(2021·四川遂宁市·中考真题)如图,在△ABC中,点D、E分别是AB、AC的中点,若△ADE的面积是3cm2,则四边形BDEC的面积为( )
A.12cm2 B.9cm2 C.6cm2 D.3cm2
4.(2020·广西贵港市·中考真题)如图,在中,点在边上,若,,且,则线段的长为( )
A.2 B. C.3 D.
5.如图,点P(8,6)在△ABC的边AC上,以原点O为位似中心,在第一象限内将△ABC缩小到原来的,得到△A′B′C′,点P在A′C′上的对应点P′的的坐标为( )
A.(4,3) B.(3,4) C.(5,3) D.(4,4)
6.(2021·四川巴中)如图,ABC中,点D、E分别在AB、AC上,且,下列结论正确的是( )
A.DE:BC=1:2
B.ADE与ABC的面积比为1:3
C.ADE与ABC的周长比为1:2
D.DEBC
7.(2020 天水)如图所示,某校数学兴趣小组利用标杆BE测量建筑物的高度,已知标杆BE高1.5m,测得AB=1.2m,BC=12.8m,则建筑物CD的高是( )
A.17.5m B.17m C.16.5m D.18m
8.(2021·山东淄博)如图,在中,是斜边上的中线,过点作交于点.若的面积为5,则的值为( )
A. B. C. D.
填空题(本题共4小题,每空3分,共15分)
9.如图,在直角坐标系中,与是位似图形,则位似中心的坐标为____________.
10.(2020·辽宁锦州)如图,在中,D是中点,,若的周长为6,则的周长为______.
11.(2021·吉林)如图,为了测量山坡的护坡石坝高,把一根长为的竹竿斜靠在石坝旁,量出竿上长为时,它离地面的高度为,则坝高为__________.
12.如图,在中,,为的中点,平分交于点,,分别与,交于点,,连接,,则的值为______;若,则的值为______.
解答题(本题共3小题,共45分)
13.(2020 福建)如图,△ADE由△ABC绕点A按逆时针方向旋转90°得到,且点B的对应点D恰好落在BC的延长线上,AD,EC相交于点P.
(1)求∠BDE的度数;
(2)F是EC延长线上的点,且∠CDF=∠DAC.
①判断DF和PF的数量关系,并证明;
②求证:.
14.如图,Rt△ABC中,∠ACB=90°,AC=BC,P为△ABC内部一点,且∠APB=∠BPC=135°.
(1)求证:△PAB∽△PBC;
(2)求证:PA=2PC;
(3)若点P到三角形的边AB,BC,CA的距离分别为h1,h2,h3,求证h12=h2·h3.
15.(2022·四川自贡)如图,用四根木条钉成矩形框,把边固定在地面上,向右推动矩形框,矩形框的形状会发生改变(四边形具有不稳定性).
(1)通过观察分析,我们发现图中线段存在等量关系,如线段由旋转得到,所以.我们还可以得到= , = ;
(2)进一步观察,我们还会发现∥,请证明这一结论;
(3)已知,若 恰好经过原矩形边的中点 ,求与之间的距离.
参考答案:
1.A 2.B 3.B 4.B 5.A 6.D 7.A 8.A
9.
10.12
11.2.7
12.
13.(1)∵△ADE由△ABC绕点A按逆时针方向旋转90°得到,
∴AB=AD,∠BAD=90°,△ABC≌△ADE,
在Rt△ABD中,∠B=∠ADB=45°,
∴∠ADE=∠B=45°,
∴∠BDE=∠ADB+∠ADE=90°.
(2)①DF=PF.
证明:由旋转的性质可知,AC=AE,∠CAE=90°,
在Rt△ACE中,∠ACE=∠AEC=45°,
∵∠CDF=∠CAD,∠ACE=∠ADB=45°,
∴∠ADB+∠CDF=∠ACE+∠CAD,
即∠FPD=∠FDP,
∴DF=PF.
②证明:过点P作PH∥ED交DF于点H,
∴∠HPF=∠DEP,,
∵∠DPF=∠ADE+∠DEP=45°+∠DEP,
∠DPF=∠ACE+∠DAC=45°+∠DAC,
∴∠DEP=∠DAC,
又∵∠CDF=∠DAC,
∴∠DEP=∠CDF,
∴∠HPF=∠CDF,
又∵FD=FP,∠F=∠F,
∴△HPF≌△CDF(ASA),
∴HF=CF,
∴DH=PC,
又∵,
∴.
14.(1)∵∠ACB=90°,AB=BC,
∴∠ABC=45°=∠PBA+∠PBC,
又∠APB=135°,∴∠PAB+∠PBA=45°,
∴∠PBC=∠PAB,
又∵∠APB=∠BPC=135°,
∴△PAB∽△PBC.
(2)∵△PAB∽△PBC,∴,
在Rt△ABC中,AB=AC,∴,
∴,
∴PA=2PC.
(3)如图,过点P作PD⊥BC,PE⊥AC交BC、AC于点D,E,
∴PF=h1,PD=h2,PE=h3,
∵∠CPB+∠APB=135°+135°=270°,
∴∠APC=90°,
∴∠EAP+∠ACP=90°,
又∵∠ACB=∠ACP+∠PCD=90°,
∴∠EAP=∠PCD,
∴Rt△AEP∽Rt△CDP,
∴,即,∴h3=2h2,
∵△PAB∽△PBC,∴,
∴,
∴.即h12=h2·h3
15.(1)
解:∵ 把边固定在地面上,向右推动矩形框,矩形框的形状会发生改变(四边形具有不稳定性).
∴由旋转的性质可知矩形ABCD的各边的长度没有改变,
∴AB=BE,EF=AD,CF=CD,
故答案为:CD,AD;
(2)
解:∵四边形ABCD是矩形,
∴ADBC,AB=CD,AD=BC,
∵AB=BE,EF=AD,CF=CD,
∴BE=CF,EF=BC,
∴四边形BEFC是平行四边形,
∴EFBC,
∴EFAD;
(3)
解:如图,过点E作EG⊥BC于点G,
∵DC=AB=BE=80cm,点H是CD的中点,
∴ CH=DH=40cm,
在Rt△BHC中,∠BCH=90°,
BH=(cm),
∵ EG⊥BC,
∴∠EGB=∠BCH=90°,
∴CHEG,
∴ △BCH∽△BGE,
∴,
∴,
∴EG=64,
∵ EFBC,
∴EF与BC之间的距离为64cm.
同课章节目录
