2023年中考数学微专题复习提升测试卷 三角形(含答案)
文档属性
| 名称 | 2023年中考数学微专题复习提升测试卷 三角形(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 106.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-07 00:00:00 | ||
图片预览


文档简介
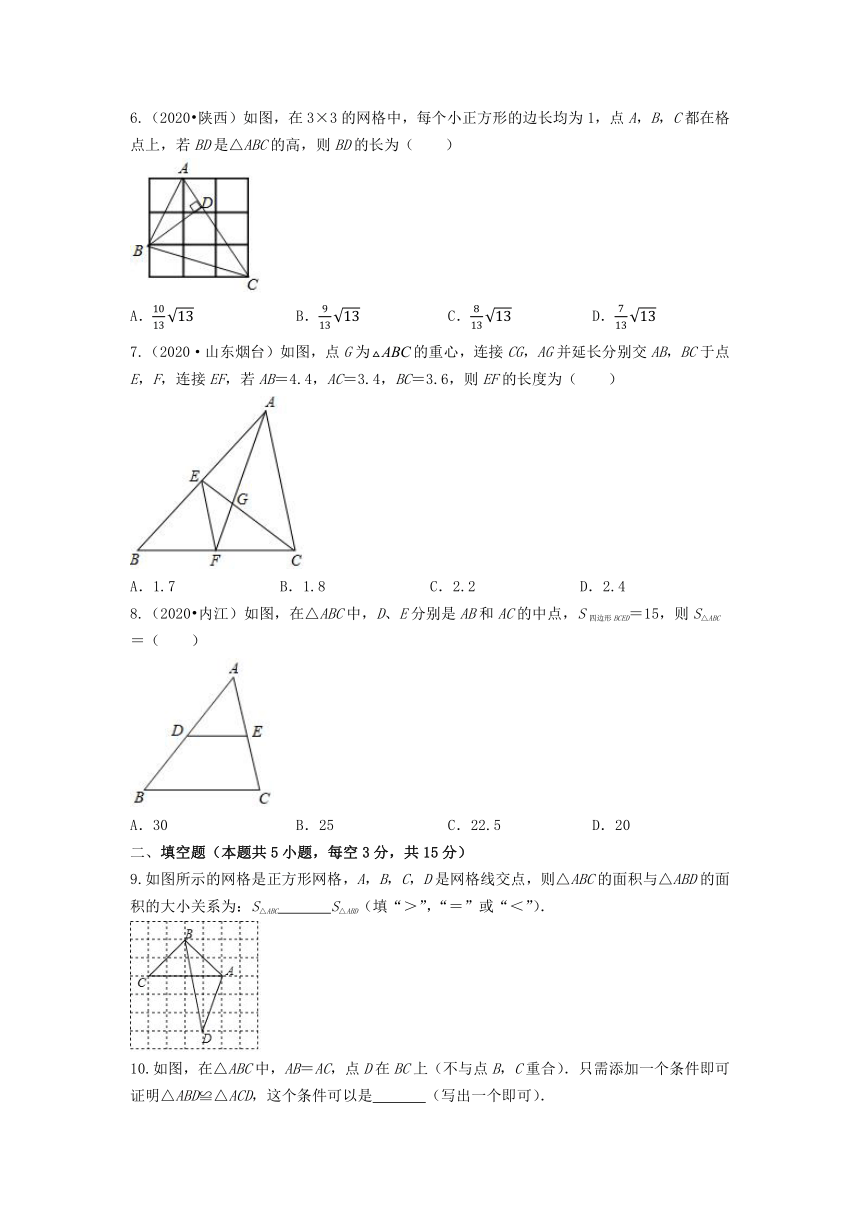
微专题复习提升测试卷——三角形
(时间:60分钟 分数:100分)
姓名: 分数:
选择题(本题共8小题,共40分)
1.(2022·江苏宿迁)若等腰三角形的两边长分别是3cm和5cm,则这个等腰三角形的周长是( )
A.8cm B.13cm C.8cm或13cm D.11cm或13cm
2.(2020 福建)如图,AD是等腰三角形ABC的顶角平分线,BD=5,则CD等于( )
A.10 B.5 C.4 D.3
3.(2022·广西贺州)如图,在Rt△ABC中,∠C=90°,∠B=56°,则∠A的度数为( )
A. B. C. D.
4.(2020 甘孜州)如图,等腰△ABC中,点D,E分别在腰AB,AC上,添加下列条件,不能判定△ABE≌△ACD的是( )
A.AD=AE B.BE=CD C.∠ADC=∠AEB D.∠DCB=∠EBC
5.(2020·山东淄博)如图,若△ABC≌△ADE,则下列结论中一定成立的是( )
A.AC=DE B.∠BAD=∠CAE C.AB=AE D.∠ABC=∠AED
6.(2020 陕西)如图,在3×3的网格中,每个小正方形的边长均为1,点A,B,C都在格点上,若BD是△ABC的高,则BD的长为( )
A. B. C. D.
7.(2020·山东烟台)如图,点G为的重心,连接CG,AG并延长分别交AB,BC于点E,F,连接EF,若AB=4.4,AC=3.4,BC=3.6,则EF的长度为( )
A.1.7 B.1.8 C.2.2 D.2.4
8.(2020 内江)如图,在△ABC中,D、E分别是AB和AC的中点,S四边形BCED=15,则S△ABC=( )
A.30 B.25 C.22.5 D.20
填空题(本题共5小题,每空3分,共15分)
9.如图所示的网格是正方形网格,A,B,C,D是网格线交点,则△ABC的面积与△ABD的面积的大小关系为:S△ABC S△ABD(填“>”,“=”或“<”).
10.如图,在△ABC中,AB=AC,点D在BC上(不与点B,C重合).只需添加一个条件即可证明△ABD≌△ACD,这个条件可以是 (写出一个即可).
11.(2022·青海西宁)如图,在△ABC中,∠C=90°,∠B=30°,AB=6,将△ABC绕点A逆时针方向旋转15°得到△AB′C′,B′C′交AB于点E,则B′E=________.
12.如图,在△ABC中,M,N分别是AB和AC的中点,连接MN,点E是CN的中点,连接ME并延长,交BC的延长线于点D.若BC=4,则CD的长为 .
13.(2021·山东聊城)如图,在△ABC中,AD⊥BC,CE⊥AB,垂足分别为点D和点E,AD与CE交于点O,连接BO并延长交AC于点F,若AB=5,BC=4,AC=6,则CE:AD:BF值为____________.
解答题(本题共3小题,共45分)
14.(2020 无锡)如图,已知AB∥CD,AB=CD,BE=CF.
求证:(1)△ABF≌△DCE;
(2)AF∥DE.
15.如图,在△ABC中,AB=AC,AD⊥BC于点D.
(1)若∠C=42°,求∠BAD的度数;
(2)若点E在边AB上,EF∥AC交AD的延长线于点F.求证:AE=FE.
16.(2020 苏州)问题1:如图①,在四边形ABCD中,∠B=∠C=90°,P是BC上一点,PA=PD,∠APD=90°.求证:AB+CD=BC.
问题2:如图②,在四边形ABCD中,∠B=∠C=45°,P是BC上一点,PA=PD,∠APD=90°.求的值.
参考答案:
1.D 2.B 3.A 4.B 5.B 6.D 7.C 8.D
9.=
10.BD=CD
11.
12.2
13.
14.证明:(1)∵AB∥CD,
∴∠B=∠C,
∵BE=CF,
∴BE﹣EF=CF﹣EF,
即BF=CE,
在△ABF和△DCE中,
∵,
∴△ABF≌△DCE(SAS);
(2)∵△ABF≌△DCE,
∴∠AFB=∠DEC,
∴∠AFE=∠DEF,
∴AF∥DE.
15.(1)∵AB=AC,AD⊥BC于点D,
∴∠BAD=∠CAD,∠ADC=90°,
又∠C=42°,∴∠BAD=∠CAD=90°-42°=48°.
(2)∵AB=AC,AD⊥BC于点D,
∴∠BAD=∠CAD,
∵EF∥AC,
∴∠F=∠CAD,
∴∠BAD=∠F,
∴AE=FE.
16.证明:(1)∵∠B=∠APD=90°,
∴∠BAP+∠APB=90°,∠APB+∠DPC=90°,
∴∠BAP=∠DPC,
又PA=PD,∠B=∠C=90°,
∴△BAP≌△CPD(AAS),
∴BP=CD,AB=PC,
∴BC=BP+PC=AB+CD;
(2)如图2,过点A作AE⊥BC于E,过点D作DF⊥BC于F,
由(1)可知,EF=AE+DF,
∵∠B=∠C=45°,AE⊥BC,DF⊥BC,
∴∠B=∠BAE=45°,∠C=∠CDF=45°,
∴BE=AE,CF=DF,ABAE,CDDF,
∴BC=BE+EF+CF=2(AE+DF),
∴.
(时间:60分钟 分数:100分)
姓名: 分数:
选择题(本题共8小题,共40分)
1.(2022·江苏宿迁)若等腰三角形的两边长分别是3cm和5cm,则这个等腰三角形的周长是( )
A.8cm B.13cm C.8cm或13cm D.11cm或13cm
2.(2020 福建)如图,AD是等腰三角形ABC的顶角平分线,BD=5,则CD等于( )
A.10 B.5 C.4 D.3
3.(2022·广西贺州)如图,在Rt△ABC中,∠C=90°,∠B=56°,则∠A的度数为( )
A. B. C. D.
4.(2020 甘孜州)如图,等腰△ABC中,点D,E分别在腰AB,AC上,添加下列条件,不能判定△ABE≌△ACD的是( )
A.AD=AE B.BE=CD C.∠ADC=∠AEB D.∠DCB=∠EBC
5.(2020·山东淄博)如图,若△ABC≌△ADE,则下列结论中一定成立的是( )
A.AC=DE B.∠BAD=∠CAE C.AB=AE D.∠ABC=∠AED
6.(2020 陕西)如图,在3×3的网格中,每个小正方形的边长均为1,点A,B,C都在格点上,若BD是△ABC的高,则BD的长为( )
A. B. C. D.
7.(2020·山东烟台)如图,点G为的重心,连接CG,AG并延长分别交AB,BC于点E,F,连接EF,若AB=4.4,AC=3.4,BC=3.6,则EF的长度为( )
A.1.7 B.1.8 C.2.2 D.2.4
8.(2020 内江)如图,在△ABC中,D、E分别是AB和AC的中点,S四边形BCED=15,则S△ABC=( )
A.30 B.25 C.22.5 D.20
填空题(本题共5小题,每空3分,共15分)
9.如图所示的网格是正方形网格,A,B,C,D是网格线交点,则△ABC的面积与△ABD的面积的大小关系为:S△ABC S△ABD(填“>”,“=”或“<”).
10.如图,在△ABC中,AB=AC,点D在BC上(不与点B,C重合).只需添加一个条件即可证明△ABD≌△ACD,这个条件可以是 (写出一个即可).
11.(2022·青海西宁)如图,在△ABC中,∠C=90°,∠B=30°,AB=6,将△ABC绕点A逆时针方向旋转15°得到△AB′C′,B′C′交AB于点E,则B′E=________.
12.如图,在△ABC中,M,N分别是AB和AC的中点,连接MN,点E是CN的中点,连接ME并延长,交BC的延长线于点D.若BC=4,则CD的长为 .
13.(2021·山东聊城)如图,在△ABC中,AD⊥BC,CE⊥AB,垂足分别为点D和点E,AD与CE交于点O,连接BO并延长交AC于点F,若AB=5,BC=4,AC=6,则CE:AD:BF值为____________.
解答题(本题共3小题,共45分)
14.(2020 无锡)如图,已知AB∥CD,AB=CD,BE=CF.
求证:(1)△ABF≌△DCE;
(2)AF∥DE.
15.如图,在△ABC中,AB=AC,AD⊥BC于点D.
(1)若∠C=42°,求∠BAD的度数;
(2)若点E在边AB上,EF∥AC交AD的延长线于点F.求证:AE=FE.
16.(2020 苏州)问题1:如图①,在四边形ABCD中,∠B=∠C=90°,P是BC上一点,PA=PD,∠APD=90°.求证:AB+CD=BC.
问题2:如图②,在四边形ABCD中,∠B=∠C=45°,P是BC上一点,PA=PD,∠APD=90°.求的值.
参考答案:
1.D 2.B 3.A 4.B 5.B 6.D 7.C 8.D
9.=
10.BD=CD
11.
12.2
13.
14.证明:(1)∵AB∥CD,
∴∠B=∠C,
∵BE=CF,
∴BE﹣EF=CF﹣EF,
即BF=CE,
在△ABF和△DCE中,
∵,
∴△ABF≌△DCE(SAS);
(2)∵△ABF≌△DCE,
∴∠AFB=∠DEC,
∴∠AFE=∠DEF,
∴AF∥DE.
15.(1)∵AB=AC,AD⊥BC于点D,
∴∠BAD=∠CAD,∠ADC=90°,
又∠C=42°,∴∠BAD=∠CAD=90°-42°=48°.
(2)∵AB=AC,AD⊥BC于点D,
∴∠BAD=∠CAD,
∵EF∥AC,
∴∠F=∠CAD,
∴∠BAD=∠F,
∴AE=FE.
16.证明:(1)∵∠B=∠APD=90°,
∴∠BAP+∠APB=90°,∠APB+∠DPC=90°,
∴∠BAP=∠DPC,
又PA=PD,∠B=∠C=90°,
∴△BAP≌△CPD(AAS),
∴BP=CD,AB=PC,
∴BC=BP+PC=AB+CD;
(2)如图2,过点A作AE⊥BC于E,过点D作DF⊥BC于F,
由(1)可知,EF=AE+DF,
∵∠B=∠C=45°,AE⊥BC,DF⊥BC,
∴∠B=∠BAE=45°,∠C=∠CDF=45°,
∴BE=AE,CF=DF,ABAE,CDDF,
∴BC=BE+EF+CF=2(AE+DF),
∴.
同课章节目录
