2023年中考数学微专题复习提升测试卷 锐角三角函数(含答案)
文档属性
| 名称 | 2023年中考数学微专题复习提升测试卷 锐角三角函数(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 275.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-07 05:59:03 | ||
图片预览

文档简介
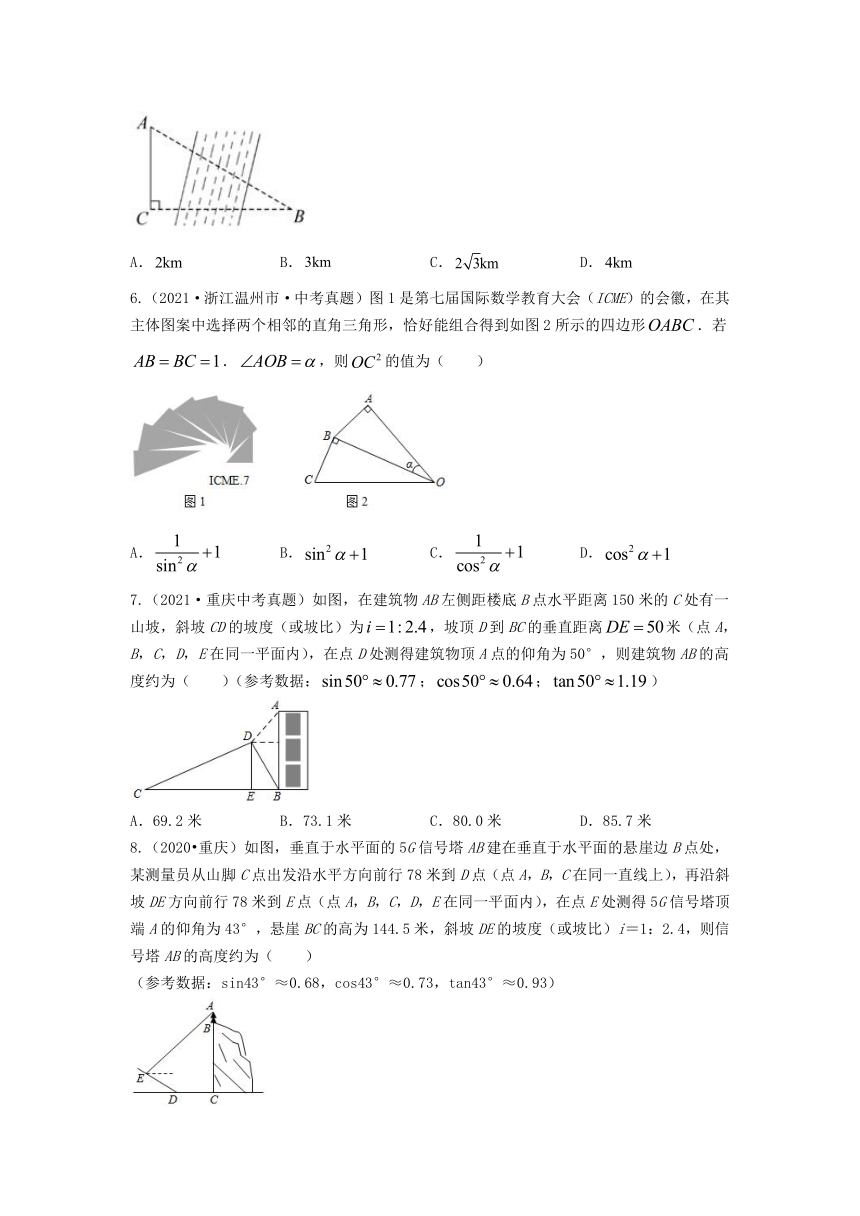
微专题复习提升测试卷——锐角三角函数
(时间:60分钟 分数:100分)
姓名: 分数:
选择题(本题共8小题,共40分)
1.(2022·天津)的值等于( )
A.2 B.1 C. D.
2.(2020 杭州)如图,在△ABC中,∠C=90°,设∠A,∠B,∠C所对的边分别为a,b,c,则( )
A.c=bsinB B.b=csinB C.a=btanB D.b=ctanB
3.(2020 凉山州)如图所示,△ABC的顶点在正方形网格的格点上,则tanA的值为( )
A. B. C.2 D.2
4.(2020·柳州市柳林中学中考真题)如图,在Rt△ABC中,∠C=90°,AB=4,AC=3,则cosB==( )
A. B. C. D.
5.(2021·福建)如图,某研究性学习小组为测量学校A与河对岸工厂B之间的距离,在学校附近选一点C,利用测量仪器测得.据此,可求得学校与工厂之间的距离等于( )
A. B. C. D.
6.(2021·浙江温州市·中考真题)图1是第七届国际数学教育大会(ICME)的会徽,在其主体图案中选择两个相邻的直角三角形,恰好能组合得到如图2所示的四边形.若.,则的值为( )
A. B. C. D.
7.(2021·重庆中考真题)如图,在建筑物AB左侧距楼底B点水平距离150米的C处有一山坡,斜坡CD的坡度(或坡比)为,坡顶D到BC的垂直距离米(点A,B,C,D,E在同一平面内),在点D处测得建筑物顶A点的仰角为50°,则建筑物AB的高度约为( )(参考数据:;;)
A.69.2米 B.73.1米 C.80.0米 D.85.7米
8.(2020 重庆)如图,垂直于水平面的5G信号塔AB建在垂直于水平面的悬崖边B点处,某测量员从山脚C点出发沿水平方向前行78米到D点(点A,B,C在同一直线上),再沿斜坡DE方向前行78米到E点(点A,B,C,D,E在同一平面内),在点E处测得5G信号塔顶端A的仰角为43°,悬崖BC的高为144.5米,斜坡DE的坡度(或坡比)i=1:2.4,则信号塔AB的高度约为( )
(参考数据:sin43°≈0.68,cos43°≈0.73,tan43°≈0.93)
A.23米 B.24米 C.24.5米 D.25米
填空题(本题共5小题,每空3分,共15分)
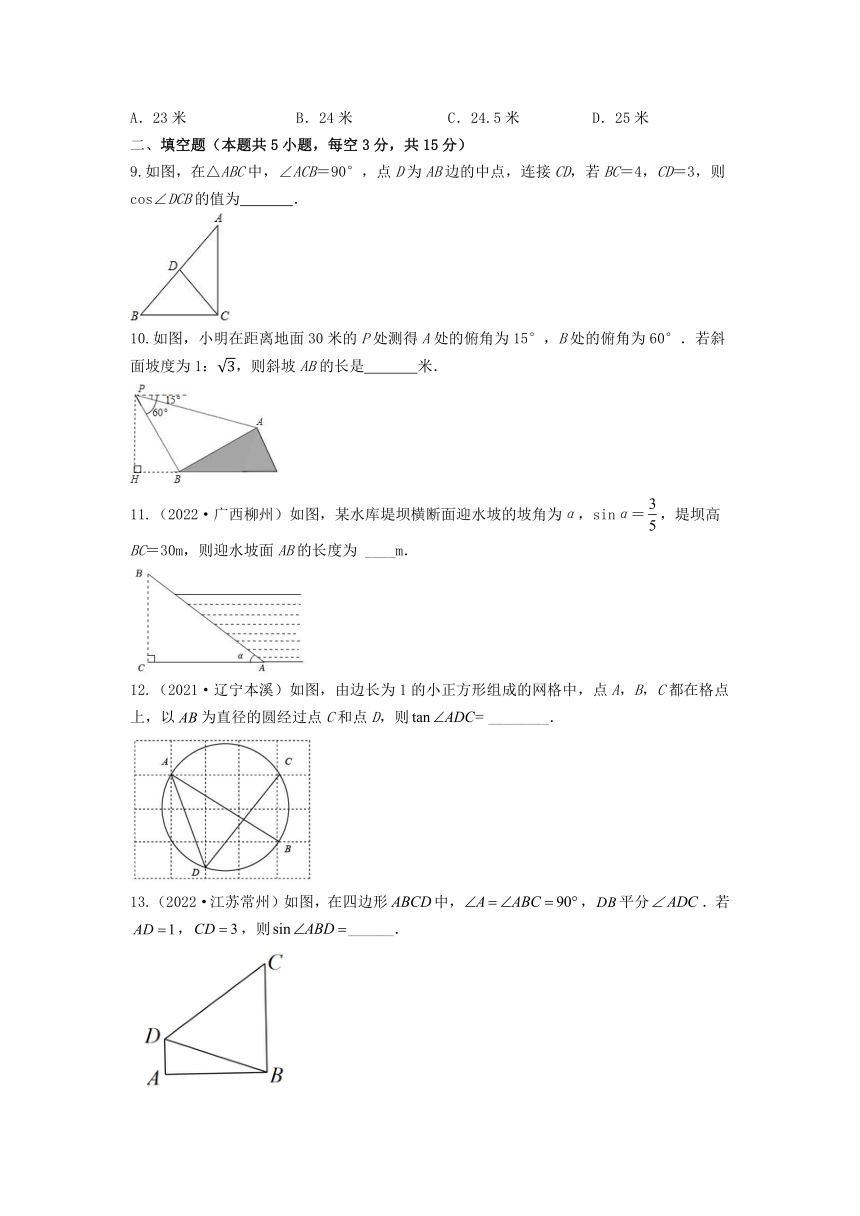
9.如图,在△ABC中,∠ACB=90°,点D为AB边的中点,连接CD,若BC=4,CD=3,则cos∠DCB的值为 .
10.如图,小明在距离地面30米的P处测得A处的俯角为15°,B处的俯角为60°.若斜面坡度为1:,则斜坡AB的长是 米.
11.(2022·广西柳州)如图,某水库堤坝横断面迎水坡的坡角为α,sinα=,堤坝高BC=30m,则迎水坡面AB的长度为 ____m.
12.(2021·辽宁本溪)如图,由边长为1的小正方形组成的网格中,点A,B,C都在格点上,以为直径的圆经过点C和点D,则________.
13.(2022·江苏常州)如图,在四边形中,,平分.若,,则______.
解答题(本题共3小题,共45分)
14.(2021·甘肃兰州)避雷针是用来保护建筑物、高大树木等避免雷击的装置.如图,小陶同学要测量垂直于地面的大楼顶部避雷针的长度(,,三点共线),在水平地面点测得,,点与大楼底部点的距离,求避雷针的长度.(结果精确到.参考数据:,,,,,)
15.(2021·四川眉山市·中考真题)“眉山水街”走红网络,成为全国各地不少游客新的打卡地!游客小何用无人机对该地一标志建筑物进行拍摄和观测,如图,无人机从处测得该建筑物顶端的俯角为24°,继续向该建筑物方向水平飞行20米到达处,测得顶端的俯角为45°,已知无人机的飞行高度为60米,则这栋建筑物的高度是多少米?(精确到0.1米,参考数据:,,)
16.(2020 黄冈)因东坡文化远近闻名的遗爱湖公园,“国庆黄金周”期间,游人络绎不绝,现有一艘游船载着游客在遗爱湖中游览,当船在A处时,船上游客发现岸上P1处的临摹亭和P2处的遗爱亭都在东北方向,当游船向正东方向行驶600m到达B处时,游客发现遗爱亭在北偏西15°方向,当游船继续向正东方向行驶400m到达C处时,游客发现临摹亭在北偏西60°方向.
(1)求A处到临摹亭P1处的距离;
(2)求临摹亭P1处于遗爱亭P2处之间的距离.(计算结果保留根号)
参考答案:
1.B 2.B 3.A 4.C 5.D 6.A 7.D 8.D
9.
10.20
11.50
12.
13.
14.解:∵,
∴,
∵,,
∴,即,
解得:m,
∵,
∴,即,
解得:m,
∴m .
15.解:过点C作交AB的延长线于点C,作于点F,如图所示:
在中,,∴,
在中,,∴,解得:,
∴
16.(1)作P1M⊥AC于M,
设P1M=x,
在Rt△P1AM中,∵∠P1AB=45°,
∴AM=P1M=x,
在Rt△P1CM中,∵∠P1CA=30°,
∴MCx,
∵AC=1000,
∴x100,解得x=500(1),
∴P1M=500(1)m
∴P1A500()m,
故A处到临摹亭P1处的距离为500()m;
(2)作BN⊥AP2于N,
∵∠P2AB=45°,∠P2BA=75°,
∴∠P2=60°,
在Rt△ABN中,∵∠P1AB=45°,AB=600m
∴BN=ANAB=300,
∴PN=500()﹣300500800,
在Rt△P2BN中,∵∠P2=60°,
∴P2NBN100,
∴P1P2=100(500800)=800400.
故临摹亭P1处于遗爱亭P2处之间的距离是(800400)m.
(时间:60分钟 分数:100分)
姓名: 分数:
选择题(本题共8小题,共40分)
1.(2022·天津)的值等于( )
A.2 B.1 C. D.
2.(2020 杭州)如图,在△ABC中,∠C=90°,设∠A,∠B,∠C所对的边分别为a,b,c,则( )
A.c=bsinB B.b=csinB C.a=btanB D.b=ctanB
3.(2020 凉山州)如图所示,△ABC的顶点在正方形网格的格点上,则tanA的值为( )
A. B. C.2 D.2
4.(2020·柳州市柳林中学中考真题)如图,在Rt△ABC中,∠C=90°,AB=4,AC=3,则cosB==( )
A. B. C. D.
5.(2021·福建)如图,某研究性学习小组为测量学校A与河对岸工厂B之间的距离,在学校附近选一点C,利用测量仪器测得.据此,可求得学校与工厂之间的距离等于( )
A. B. C. D.
6.(2021·浙江温州市·中考真题)图1是第七届国际数学教育大会(ICME)的会徽,在其主体图案中选择两个相邻的直角三角形,恰好能组合得到如图2所示的四边形.若.,则的值为( )
A. B. C. D.
7.(2021·重庆中考真题)如图,在建筑物AB左侧距楼底B点水平距离150米的C处有一山坡,斜坡CD的坡度(或坡比)为,坡顶D到BC的垂直距离米(点A,B,C,D,E在同一平面内),在点D处测得建筑物顶A点的仰角为50°,则建筑物AB的高度约为( )(参考数据:;;)
A.69.2米 B.73.1米 C.80.0米 D.85.7米
8.(2020 重庆)如图,垂直于水平面的5G信号塔AB建在垂直于水平面的悬崖边B点处,某测量员从山脚C点出发沿水平方向前行78米到D点(点A,B,C在同一直线上),再沿斜坡DE方向前行78米到E点(点A,B,C,D,E在同一平面内),在点E处测得5G信号塔顶端A的仰角为43°,悬崖BC的高为144.5米,斜坡DE的坡度(或坡比)i=1:2.4,则信号塔AB的高度约为( )
(参考数据:sin43°≈0.68,cos43°≈0.73,tan43°≈0.93)
A.23米 B.24米 C.24.5米 D.25米
填空题(本题共5小题,每空3分,共15分)
9.如图,在△ABC中,∠ACB=90°,点D为AB边的中点,连接CD,若BC=4,CD=3,则cos∠DCB的值为 .
10.如图,小明在距离地面30米的P处测得A处的俯角为15°,B处的俯角为60°.若斜面坡度为1:,则斜坡AB的长是 米.
11.(2022·广西柳州)如图,某水库堤坝横断面迎水坡的坡角为α,sinα=,堤坝高BC=30m,则迎水坡面AB的长度为 ____m.
12.(2021·辽宁本溪)如图,由边长为1的小正方形组成的网格中,点A,B,C都在格点上,以为直径的圆经过点C和点D,则________.
13.(2022·江苏常州)如图,在四边形中,,平分.若,,则______.
解答题(本题共3小题,共45分)
14.(2021·甘肃兰州)避雷针是用来保护建筑物、高大树木等避免雷击的装置.如图,小陶同学要测量垂直于地面的大楼顶部避雷针的长度(,,三点共线),在水平地面点测得,,点与大楼底部点的距离,求避雷针的长度.(结果精确到.参考数据:,,,,,)
15.(2021·四川眉山市·中考真题)“眉山水街”走红网络,成为全国各地不少游客新的打卡地!游客小何用无人机对该地一标志建筑物进行拍摄和观测,如图,无人机从处测得该建筑物顶端的俯角为24°,继续向该建筑物方向水平飞行20米到达处,测得顶端的俯角为45°,已知无人机的飞行高度为60米,则这栋建筑物的高度是多少米?(精确到0.1米,参考数据:,,)
16.(2020 黄冈)因东坡文化远近闻名的遗爱湖公园,“国庆黄金周”期间,游人络绎不绝,现有一艘游船载着游客在遗爱湖中游览,当船在A处时,船上游客发现岸上P1处的临摹亭和P2处的遗爱亭都在东北方向,当游船向正东方向行驶600m到达B处时,游客发现遗爱亭在北偏西15°方向,当游船继续向正东方向行驶400m到达C处时,游客发现临摹亭在北偏西60°方向.
(1)求A处到临摹亭P1处的距离;
(2)求临摹亭P1处于遗爱亭P2处之间的距离.(计算结果保留根号)
参考答案:
1.B 2.B 3.A 4.C 5.D 6.A 7.D 8.D
9.
10.20
11.50
12.
13.
14.解:∵,
∴,
∵,,
∴,即,
解得:m,
∵,
∴,即,
解得:m,
∴m .
15.解:过点C作交AB的延长线于点C,作于点F,如图所示:
在中,,∴,
在中,,∴,解得:,
∴
16.(1)作P1M⊥AC于M,
设P1M=x,
在Rt△P1AM中,∵∠P1AB=45°,
∴AM=P1M=x,
在Rt△P1CM中,∵∠P1CA=30°,
∴MCx,
∵AC=1000,
∴x100,解得x=500(1),
∴P1M=500(1)m
∴P1A500()m,
故A处到临摹亭P1处的距离为500()m;
(2)作BN⊥AP2于N,
∵∠P2AB=45°,∠P2BA=75°,
∴∠P2=60°,
在Rt△ABN中,∵∠P1AB=45°,AB=600m
∴BN=ANAB=300,
∴PN=500()﹣300500800,
在Rt△P2BN中,∵∠P2=60°,
∴P2NBN100,
∴P1P2=100(500800)=800400.
故临摹亭P1处于遗爱亭P2处之间的距离是(800400)m.
同课章节目录
