2023年中考数学微专题复习提升测试卷 平行四边形与特殊的平行四边形(含答案)
文档属性
| 名称 | 2023年中考数学微专题复习提升测试卷 平行四边形与特殊的平行四边形(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 251.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-07 00:00:00 | ||
图片预览

文档简介
微专题复习提升测试卷——平行四边形与特殊的平行四边形
(时间:60分钟 分数:100分)
姓名: 分数:
选择题(本题共8小题,共40分)
1.(2022·广东)如图,在中,一定正确的是( )
A. B. C. D.
2.(2021·山东泰安市·中考真题)如图,在平行四边形中,E是的中点,则下列四个结论:①;②若,,则;③若,则;④若,则与全等.其中正确结论的个数为( )
A.1个 B.2个 C.3个 D.4个
3.(2020 荆门)如图,菱形ABCD中,E,F分别是AD,BD的中点,若EF=5,则菱形ABCD的周长为( )
A.20 B.30 C.40 D.50
4.(2021·广西柳州)如图,在菱形中,对角线,则的面积为( )
A.9 B.10 C.11 D.12
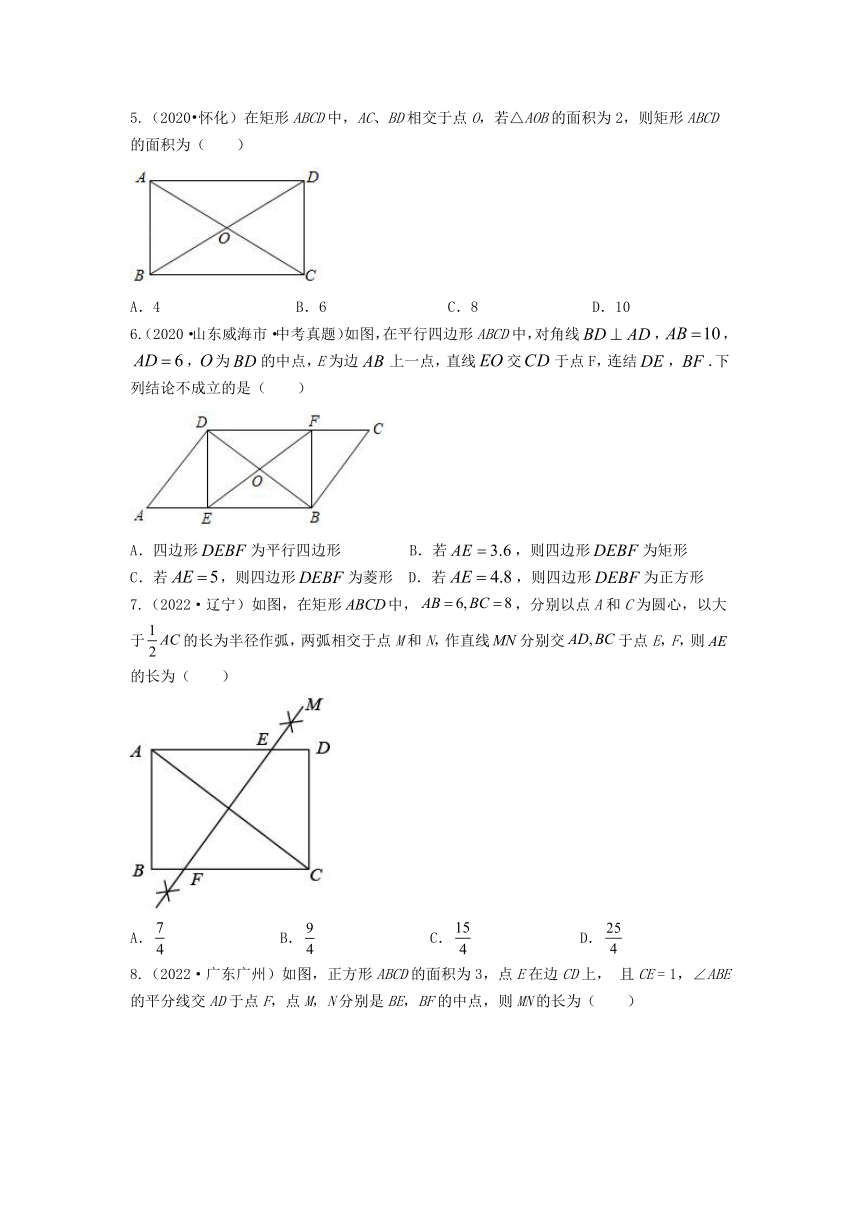
5.(2020 怀化)在矩形ABCD中,AC、BD相交于点O,若△AOB的面积为2,则矩形ABCD的面积为( )
A.4 B.6 C.8 D.10
6.(2020·山东威海市·中考真题)如图,在平行四边形ABCD中,对角线,,,为的中点,E为边上一点,直线交于点F,连结,.下列结论不成立的是( )
A.四边形为平行四边形 B.若,则四边形为矩形
C.若,则四边形为菱形 D.若,则四边形为正方形
7.(2022·辽宁)如图,在矩形中,,分别以点A和C为圆心,以大于的长为半径作弧,两弧相交于点M和N,作直线分别交于点E,F,则的长为( )
A. B. C. D.
8.(2022·广东广州)如图,正方形ABCD的面积为3,点E在边CD上, 且CE = 1,∠ABE的平分线交AD于点F,点M,N分别是BE,BF的中点,则MN的长为( )
A. B.
C. D.
填空题(本题共5小题,每空3分,共15分)
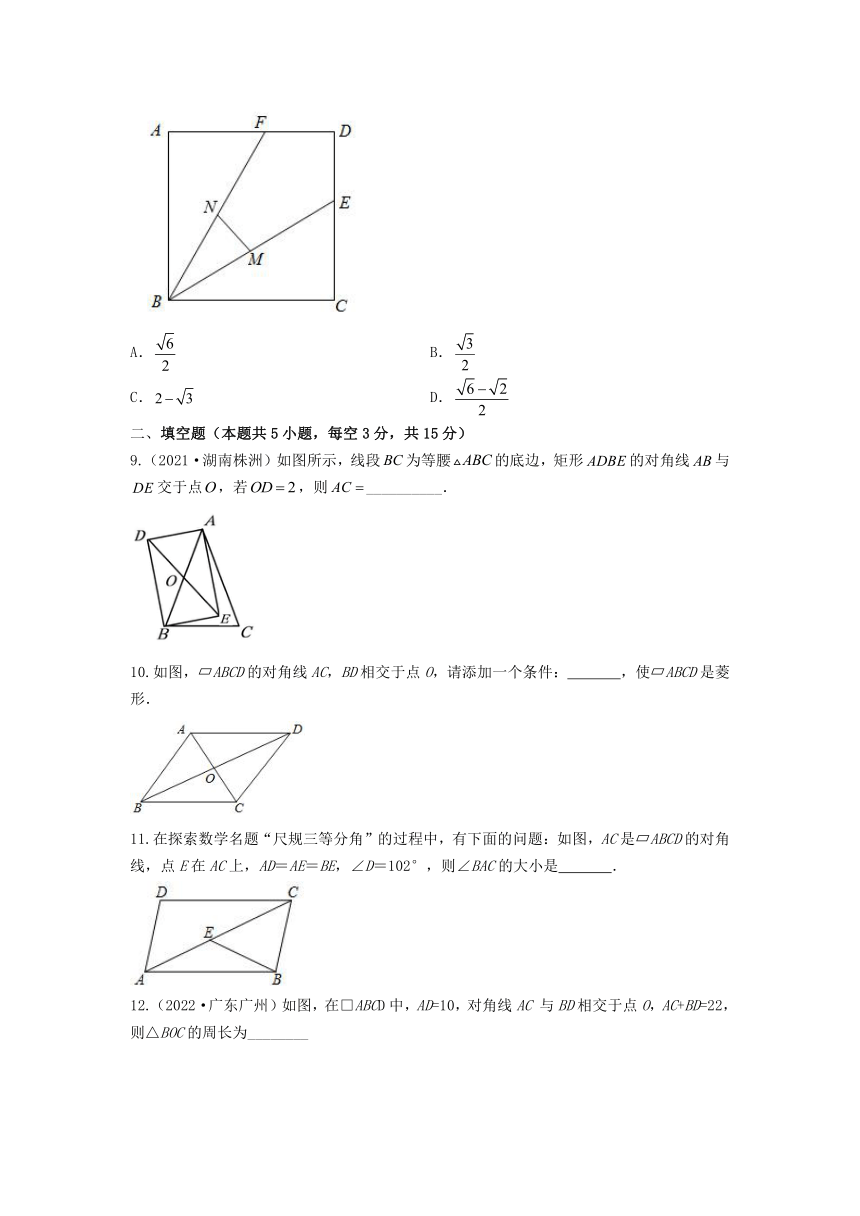
9.(2021·湖南株洲)如图所示,线段为等腰的底边,矩形的对角线与交于点,若,则__________.
10.如图, ABCD的对角线AC,BD相交于点O,请添加一个条件: ,使 ABCD是菱形.
11.在探索数学名题“尺规三等分角”的过程中,有下面的问题:如图,AC是 ABCD的对角线,点E在AC上,AD=AE=BE,∠D=102°,则∠BAC的大小是 .
12.(2022·广东广州)如图,在□ABCD中,AD=10,对角线AC 与BD相交于点O,AC+BD=22,则△BOC的周长为________
13.如图,在菱形ABCD中,对角线AC,BD交于点O,其中OA=1,OB=2,则菱形ABCD的面积为 .
解答题(本题共3小题,共45分)
14.(2020·湖南娄底)如图,中,,,分别在边、上的点E与点F关于对称,连接、、、.
(1)试判定四边形的形状,并说明理由;
(2)求证:
15.(2020 鄂州)如图,在平行四边形ABCD中,对角线AC与BD交于点O,点M,N分别为OA、OC的中点,延长BM至点E,使EM=BM,连接DE.
(1)求证:△AMB≌△CND;
(2)若BD=2AB,且AB=5,DN=4,求四边形DEMN的面积.
16.如图,已知正方形ABCD的边长为1,正方形CEFG的面积为,点E在CD边上,点G在BC的延长线上,设以线段AD和DE为邻边的矩形的面积为,且.
(1)求线段CE的长;
(2)若点H为BC边的中点,连结HD,求证:.
参考答案:
1.C 2.D 3.C 4.B 5.C 6.D 7.D 8.D
9.4
10.AD=DC
11.26°
12.21
13.4
14.解:(1)四边形为菱形,理由如下
由可得,从而
设与相交于点O
∵点E与点F关于对称
∴且
在和中
∴
∴,又
∴四边形为菱形,
(2)∵,据(1)C
∴
又∵∴
∴.
15.(1)∵平行四边形ABCD中,对角线AC与BD交于点O,
∴AO=CO,
又∵点M,N分别为OA、OC的中点,
∴AM=CN,
∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴∠BAM=∠DCN,
∴△AMB≌△CND(SAS);
(2)∵△AMB≌△CND,
∴BM=DN,∠ABM=∠CDN,
又∵BM=EM,
∴DN=EM,
∵AB∥CD,
∴∠ABO=∠CDO,
∴∠MBO=∠NDO,
∴ME∥DN
∴四边形DEMN是平行四边形,
∵BD=2AB,BD=2BO,
∴AB=OB,
又∵M是AO的中点,
∴BM⊥AO,
∴∠EMN=90°,
∴四边形DEMN是矩形,
∵AB=5,DN=BM=4,
∴AM=3=MO,
∴MN=6,
∴矩形DEMN的面积=6×4=24.
16.根据题意,得AD=BC=CD=1,∠BCD=90°.
(1)设CE=x(0因为S1=S2,所以x2=1-x,
解得x=(负根已舍去),即CE=.
(2)因为点H为BC边的中点,
所以CH=,所以HD=,
因为CG=CE=,点H,C,G在同一直线上,
所以HG=HC+CG=+=,所以HD=HG.
(时间:60分钟 分数:100分)
姓名: 分数:
选择题(本题共8小题,共40分)
1.(2022·广东)如图,在中,一定正确的是( )
A. B. C. D.
2.(2021·山东泰安市·中考真题)如图,在平行四边形中,E是的中点,则下列四个结论:①;②若,,则;③若,则;④若,则与全等.其中正确结论的个数为( )
A.1个 B.2个 C.3个 D.4个
3.(2020 荆门)如图,菱形ABCD中,E,F分别是AD,BD的中点,若EF=5,则菱形ABCD的周长为( )
A.20 B.30 C.40 D.50
4.(2021·广西柳州)如图,在菱形中,对角线,则的面积为( )
A.9 B.10 C.11 D.12
5.(2020 怀化)在矩形ABCD中,AC、BD相交于点O,若△AOB的面积为2,则矩形ABCD的面积为( )
A.4 B.6 C.8 D.10
6.(2020·山东威海市·中考真题)如图,在平行四边形ABCD中,对角线,,,为的中点,E为边上一点,直线交于点F,连结,.下列结论不成立的是( )
A.四边形为平行四边形 B.若,则四边形为矩形
C.若,则四边形为菱形 D.若,则四边形为正方形
7.(2022·辽宁)如图,在矩形中,,分别以点A和C为圆心,以大于的长为半径作弧,两弧相交于点M和N,作直线分别交于点E,F,则的长为( )
A. B. C. D.
8.(2022·广东广州)如图,正方形ABCD的面积为3,点E在边CD上, 且CE = 1,∠ABE的平分线交AD于点F,点M,N分别是BE,BF的中点,则MN的长为( )
A. B.
C. D.
填空题(本题共5小题,每空3分,共15分)
9.(2021·湖南株洲)如图所示,线段为等腰的底边,矩形的对角线与交于点,若,则__________.
10.如图, ABCD的对角线AC,BD相交于点O,请添加一个条件: ,使 ABCD是菱形.
11.在探索数学名题“尺规三等分角”的过程中,有下面的问题:如图,AC是 ABCD的对角线,点E在AC上,AD=AE=BE,∠D=102°,则∠BAC的大小是 .
12.(2022·广东广州)如图,在□ABCD中,AD=10,对角线AC 与BD相交于点O,AC+BD=22,则△BOC的周长为________
13.如图,在菱形ABCD中,对角线AC,BD交于点O,其中OA=1,OB=2,则菱形ABCD的面积为 .
解答题(本题共3小题,共45分)
14.(2020·湖南娄底)如图,中,,,分别在边、上的点E与点F关于对称,连接、、、.
(1)试判定四边形的形状,并说明理由;
(2)求证:
15.(2020 鄂州)如图,在平行四边形ABCD中,对角线AC与BD交于点O,点M,N分别为OA、OC的中点,延长BM至点E,使EM=BM,连接DE.
(1)求证:△AMB≌△CND;
(2)若BD=2AB,且AB=5,DN=4,求四边形DEMN的面积.
16.如图,已知正方形ABCD的边长为1,正方形CEFG的面积为,点E在CD边上,点G在BC的延长线上,设以线段AD和DE为邻边的矩形的面积为,且.
(1)求线段CE的长;
(2)若点H为BC边的中点,连结HD,求证:.
参考答案:
1.C 2.D 3.C 4.B 5.C 6.D 7.D 8.D
9.4
10.AD=DC
11.26°
12.21
13.4
14.解:(1)四边形为菱形,理由如下
由可得,从而
设与相交于点O
∵点E与点F关于对称
∴且
在和中
∴
∴,又
∴四边形为菱形,
(2)∵,据(1)C
∴
又∵∴
∴.
15.(1)∵平行四边形ABCD中,对角线AC与BD交于点O,
∴AO=CO,
又∵点M,N分别为OA、OC的中点,
∴AM=CN,
∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴∠BAM=∠DCN,
∴△AMB≌△CND(SAS);
(2)∵△AMB≌△CND,
∴BM=DN,∠ABM=∠CDN,
又∵BM=EM,
∴DN=EM,
∵AB∥CD,
∴∠ABO=∠CDO,
∴∠MBO=∠NDO,
∴ME∥DN
∴四边形DEMN是平行四边形,
∵BD=2AB,BD=2BO,
∴AB=OB,
又∵M是AO的中点,
∴BM⊥AO,
∴∠EMN=90°,
∴四边形DEMN是矩形,
∵AB=5,DN=BM=4,
∴AM=3=MO,
∴MN=6,
∴矩形DEMN的面积=6×4=24.
16.根据题意,得AD=BC=CD=1,∠BCD=90°.
(1)设CE=x(0
解得x=(负根已舍去),即CE=.
(2)因为点H为BC边的中点,
所以CH=,所以HD=,
因为CG=CE=,点H,C,G在同一直线上,
所以HG=HC+CG=+=,所以HD=HG.
同课章节目录
