2023年中考数学微专题复习提升测试卷 平面直角坐标系与一次函数(含答案)
文档属性
| 名称 | 2023年中考数学微专题复习提升测试卷 平面直角坐标系与一次函数(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 111.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-07 06:02:18 | ||
图片预览


文档简介
微专题复习提升测试卷——平面直角坐标系与一次函数
(时间:60分钟 分数:100分)
姓名: 分数:
选择题(本题共8小题,共40分)
1.(2022·内蒙古包头)在一次函数中,y的值随x值的增大而增大,且,则点在( )
A.第四象限 B.第三象限 C.第二象限 D.第一象限
2.(2020 泰州)点P(a,b)在函数y=3x+2的图象上,则代数式6a﹣2b+1的值等于( )
A.5 B.3 C.﹣3 D.﹣1
3.(2021·湖南邵阳)在平面直角坐标系中,若直线不经过第一象限,则关于的方程的实数根的个数为( )
A.0个 B.1个 C.2个 D.1或2个
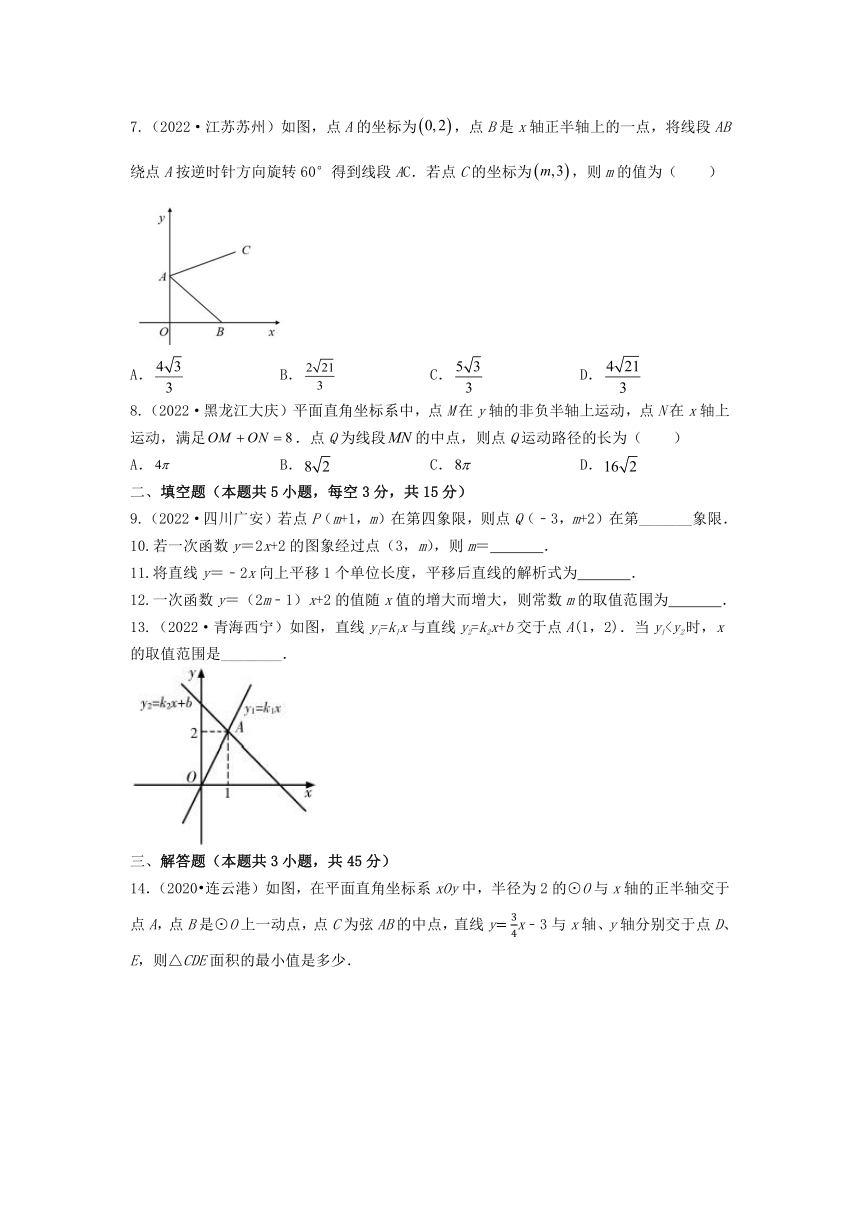
4.(2020 乐山)直线y=kx+b在平面直角坐标系中的位置如图所示,则不等式kx+b≤2的解集是( )
A.x≤﹣2 B.x≤﹣4 C.x≥﹣2 D.x≥﹣4
5.(2021·安徽中考真题)某品牌鞋子的长度ycm与鞋子的“码”数x之间满足一次函数关系.若22码鞋子的长度为16cm,44码鞋子的长度为27cm,则38码鞋子的长度为( )
A.23cm B.24cm C.25cm D.26cm
6.(2021·四川自贡)如图,,,以点A为圆心,AC长为半径画弧,交y轴正半轴于点B,则点B的坐标为( )
A. B. C. D.
7.(2022·江苏苏州)如图,点A的坐标为,点B是x轴正半轴上的一点,将线段AB绕点A按逆时针方向旋转60°得到线段AC.若点C的坐标为,则m的值为( )
A. B. C. D.
8.(2022·黑龙江大庆)平面直角坐标系中,点M在y轴的非负半轴上运动,点N在x轴上运动,满足.点Q为线段的中点,则点Q运动路径的长为( )
A. B. C. D.
填空题(本题共5小题,每空3分,共15分)
9.(2022·四川广安)若点P(m+1,m)在第四象限,则点Q(﹣3,m+2)在第_______象限.
10.若一次函数y=2x+2的图象经过点(3,m),则m= .
11.将直线y=﹣2x向上平移1个单位长度,平移后直线的解析式为 .
12.一次函数y=(2m﹣1)x+2的值随x值的增大而增大,则常数m的取值范围为 .
13.(2022·青海西宁)如图,直线y1=k1x与直线y2=k2x+b交于点A(1,2).当y1解答题(本题共3小题,共45分)
14.(2020 连云港)如图,在平面直角坐标系xOy中,半径为2的⊙O与x轴的正半轴交于点A,点B是⊙O上一动点,点C为弦AB的中点,直线yx﹣3与x轴、y轴分别交于点D、E,则△CDE面积的最小值是多少.
15.(2020 黑龙江)为抗击疫情,支持武汉,某物流公司的快递车和货车每天往返于物流公司、武汉两地,快递车比货车多往返一趟,如图表示两车离物流公司的距离y(单位:千米)与快递车所用时间x(单位:时)的函数图象,已知货车比快递车早1小时出发,到达武汉后用2小时装卸货物,按原速、原路返回,货车比快递车最后一次返回物流公司晚1小时.
(1)求ME的函数解析式;
(2)求快递车第二次往返过程中,与货车相遇的时间.
(3)求两车最后一次相遇时离武汉的距离.(直接写出答案)
16.某生态体验园推出了甲、乙两种消费卡,设入园次数为x时所需费用为y元,选择这两种卡消费时,y与x的函数关系如图所示,解答下列问题:
(1)分别求出选择这两种卡消费时,y关于x的函数表达式;
(2)请根据入园次数确定选择哪种卡消费比较合算.
参考答案:
1.B 2.C 3.D 4.C 5.B 6.D 7.C 8.B
9.二
10.8
11.y=﹣2x+1
12.m
13.
14.如图,连接OB,取OA的中点M,连接CM,过点M作MN⊥DE于N.
∵AC=CB,AM=OM,
∴MCOB=1,
∴点C的运动轨迹是以M为圆心,1为半径的⊙M,设⊙M交MN于C′.
∵直线yx﹣3与x轴、y轴分别交于点D、E,
∴D(4,0),E(0,﹣3),
∴OD=4,OE=3,
∴DE5,
∵∠MDN=∠ODE,∠MND=∠DOE,
∴△DNM∽△DOE,
∴,
∴,
∴MN,
当点C与C′重合时,△C′DE的面积最小,最小值5×(1)=2,
故答案为2.
15.(1)设ME的函数解析式为y=kx+b(k≠0),由ME经过(0,50),(3,200)可得:
,解得,
∴ME的解析式为y=50x+50;
(2)设BC的函数解析式为y=mx+n,由BC经过(4,0),(6,200)可得:
,解得,
∴BC的函数解析式为y=100x﹣400;
设FG的函数解析式为y=px+q,由FG经过(5,200),(9,0)可得:
,解得,
∴FG的函数解析式为y=﹣50x+450,
解方程组得,
同理可得x=7h,
答:货车返回时与快递车图中相遇的时间h,7h;
(3)(9﹣7)×50=100(km),
答:两车最后一次相遇时离武汉的距离为100km.
16.(1)设y甲=k1x,根据题意得5k1=100,解得k1=20,∴y甲=20x;
设y乙=k2x+100,根据题意得:20k2+100=300,解得k2=10,∴y乙=10x+100.
(2)①y甲②y甲=y乙,即20x=10x+100,解得x=10,当入园次数等于10次时,选择两种消费卡费用一样;
③y甲>y乙,即20x>10x+100,解得x>10,当入园次数大于10次时,选择乙消费卡比较合算
(时间:60分钟 分数:100分)
姓名: 分数:
选择题(本题共8小题,共40分)
1.(2022·内蒙古包头)在一次函数中,y的值随x值的增大而增大,且,则点在( )
A.第四象限 B.第三象限 C.第二象限 D.第一象限
2.(2020 泰州)点P(a,b)在函数y=3x+2的图象上,则代数式6a﹣2b+1的值等于( )
A.5 B.3 C.﹣3 D.﹣1
3.(2021·湖南邵阳)在平面直角坐标系中,若直线不经过第一象限,则关于的方程的实数根的个数为( )
A.0个 B.1个 C.2个 D.1或2个
4.(2020 乐山)直线y=kx+b在平面直角坐标系中的位置如图所示,则不等式kx+b≤2的解集是( )
A.x≤﹣2 B.x≤﹣4 C.x≥﹣2 D.x≥﹣4
5.(2021·安徽中考真题)某品牌鞋子的长度ycm与鞋子的“码”数x之间满足一次函数关系.若22码鞋子的长度为16cm,44码鞋子的长度为27cm,则38码鞋子的长度为( )
A.23cm B.24cm C.25cm D.26cm
6.(2021·四川自贡)如图,,,以点A为圆心,AC长为半径画弧,交y轴正半轴于点B,则点B的坐标为( )
A. B. C. D.
7.(2022·江苏苏州)如图,点A的坐标为,点B是x轴正半轴上的一点,将线段AB绕点A按逆时针方向旋转60°得到线段AC.若点C的坐标为,则m的值为( )
A. B. C. D.
8.(2022·黑龙江大庆)平面直角坐标系中,点M在y轴的非负半轴上运动,点N在x轴上运动,满足.点Q为线段的中点,则点Q运动路径的长为( )
A. B. C. D.
填空题(本题共5小题,每空3分,共15分)
9.(2022·四川广安)若点P(m+1,m)在第四象限,则点Q(﹣3,m+2)在第_______象限.
10.若一次函数y=2x+2的图象经过点(3,m),则m= .
11.将直线y=﹣2x向上平移1个单位长度,平移后直线的解析式为 .
12.一次函数y=(2m﹣1)x+2的值随x值的增大而增大,则常数m的取值范围为 .
13.(2022·青海西宁)如图,直线y1=k1x与直线y2=k2x+b交于点A(1,2).当y1
14.(2020 连云港)如图,在平面直角坐标系xOy中,半径为2的⊙O与x轴的正半轴交于点A,点B是⊙O上一动点,点C为弦AB的中点,直线yx﹣3与x轴、y轴分别交于点D、E,则△CDE面积的最小值是多少.
15.(2020 黑龙江)为抗击疫情,支持武汉,某物流公司的快递车和货车每天往返于物流公司、武汉两地,快递车比货车多往返一趟,如图表示两车离物流公司的距离y(单位:千米)与快递车所用时间x(单位:时)的函数图象,已知货车比快递车早1小时出发,到达武汉后用2小时装卸货物,按原速、原路返回,货车比快递车最后一次返回物流公司晚1小时.
(1)求ME的函数解析式;
(2)求快递车第二次往返过程中,与货车相遇的时间.
(3)求两车最后一次相遇时离武汉的距离.(直接写出答案)
16.某生态体验园推出了甲、乙两种消费卡,设入园次数为x时所需费用为y元,选择这两种卡消费时,y与x的函数关系如图所示,解答下列问题:
(1)分别求出选择这两种卡消费时,y关于x的函数表达式;
(2)请根据入园次数确定选择哪种卡消费比较合算.
参考答案:
1.B 2.C 3.D 4.C 5.B 6.D 7.C 8.B
9.二
10.8
11.y=﹣2x+1
12.m
13.
14.如图,连接OB,取OA的中点M,连接CM,过点M作MN⊥DE于N.
∵AC=CB,AM=OM,
∴MCOB=1,
∴点C的运动轨迹是以M为圆心,1为半径的⊙M,设⊙M交MN于C′.
∵直线yx﹣3与x轴、y轴分别交于点D、E,
∴D(4,0),E(0,﹣3),
∴OD=4,OE=3,
∴DE5,
∵∠MDN=∠ODE,∠MND=∠DOE,
∴△DNM∽△DOE,
∴,
∴,
∴MN,
当点C与C′重合时,△C′DE的面积最小,最小值5×(1)=2,
故答案为2.
15.(1)设ME的函数解析式为y=kx+b(k≠0),由ME经过(0,50),(3,200)可得:
,解得,
∴ME的解析式为y=50x+50;
(2)设BC的函数解析式为y=mx+n,由BC经过(4,0),(6,200)可得:
,解得,
∴BC的函数解析式为y=100x﹣400;
设FG的函数解析式为y=px+q,由FG经过(5,200),(9,0)可得:
,解得,
∴FG的函数解析式为y=﹣50x+450,
解方程组得,
同理可得x=7h,
答:货车返回时与快递车图中相遇的时间h,7h;
(3)(9﹣7)×50=100(km),
答:两车最后一次相遇时离武汉的距离为100km.
16.(1)设y甲=k1x,根据题意得5k1=100,解得k1=20,∴y甲=20x;
设y乙=k2x+100,根据题意得:20k2+100=300,解得k2=10,∴y乙=10x+100.
(2)①y甲
③y甲>y乙,即20x>10x+100,解得x>10,当入园次数大于10次时,选择乙消费卡比较合算
同课章节目录
