2023年中考数学微专题复习提升测试卷 反比例函数(含答案)
文档属性
| 名称 | 2023年中考数学微专题复习提升测试卷 反比例函数(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 163.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-07 06:09:11 | ||
图片预览

文档简介
微专题复习提升测试卷——反比例函数
(时间:60分钟 分数:100分)
姓名: 分数:
选择题(本题共8小题,共40分)
1.(2020 金华)已知点(﹣2,a)(2,b)(3,c)在函数y(k>0)的图象上,则下列判断正确的是( )
A.a<b<c B.b<a<c C.a<c<b D.c<b<a
2.(2021·山西)已知反比例函数,则下列描述不正确的是( )
A.图象位于第一,第三象限 B.图象必经过点
C.图象不可能与坐标轴相交 D.随的增大而减小
3.(2020·广西贺州)在反比例函数中,当时,y的值为( )
A.2 B. C. D.
4.(2020 无锡)反比例函数y与一次函数y的图形有一个交点B(,m),则k的值为( )
A.1 B.2 C. D.
5.(2021·广西梧州)如图,在同一平面直角坐标系中,直线y=t(t为常数)与反比例函数y1,y2的图象分别交于点A,B,连接OA,OB,则△OAB的面积为( )
A.5t B. C. D.5
6.(2021·江苏连云港)关于某个函数表达式,甲、乙、丙三位同学都正确地说出了该函数的一个特征.甲:函数图像经过点;乙:函数图像经过第四象限;
丙:当时,y随x的增大而增大.则这个函数表达式可能是( )
A. B. C. D.
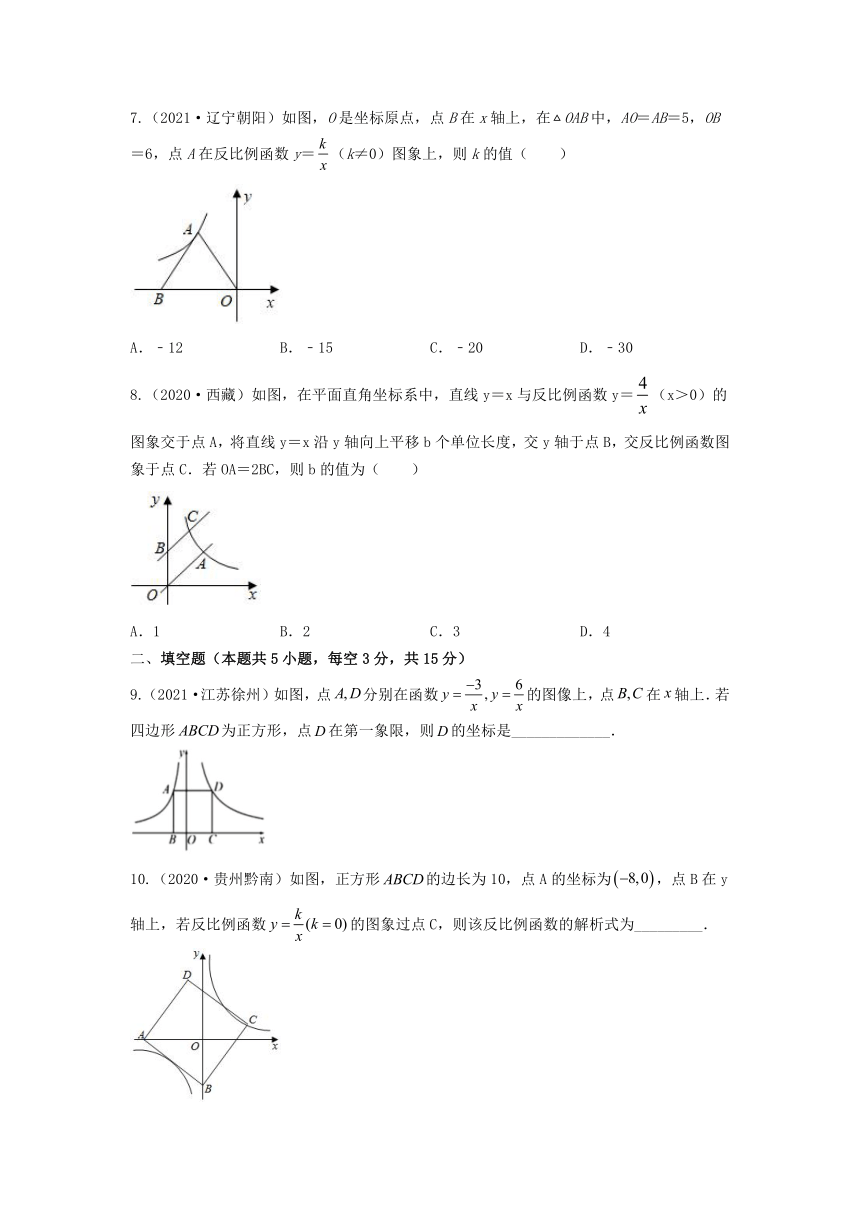
7.(2021·辽宁朝阳)如图,O是坐标原点,点B在x轴上,在OAB中,AO=AB=5,OB=6,点A在反比例函数y=(k≠0)图象上,则k的值( )
A.﹣12 B.﹣15 C.﹣20 D.﹣30
8.(2020·西藏)如图,在平面直角坐标系中,直线y=x与反比例函数y=(x>0)的图象交于点A,将直线y=x沿y轴向上平移b个单位长度,交y轴于点B,交反比例函数图象于点C.若OA=2BC,则b的值为( )
A.1 B.2 C.3 D.4
填空题(本题共5小题,每空3分,共15分)
9.(2021·江苏徐州)如图,点分别在函数的图像上,点在轴上.若四边形为正方形,点在第一象限,则的坐标是_____________.
10.(2020·贵州黔南)如图,正方形的边长为10,点A的坐标为,点B在y轴上,若反比例函数的图象过点C,则该反比例函数的解析式为_________.
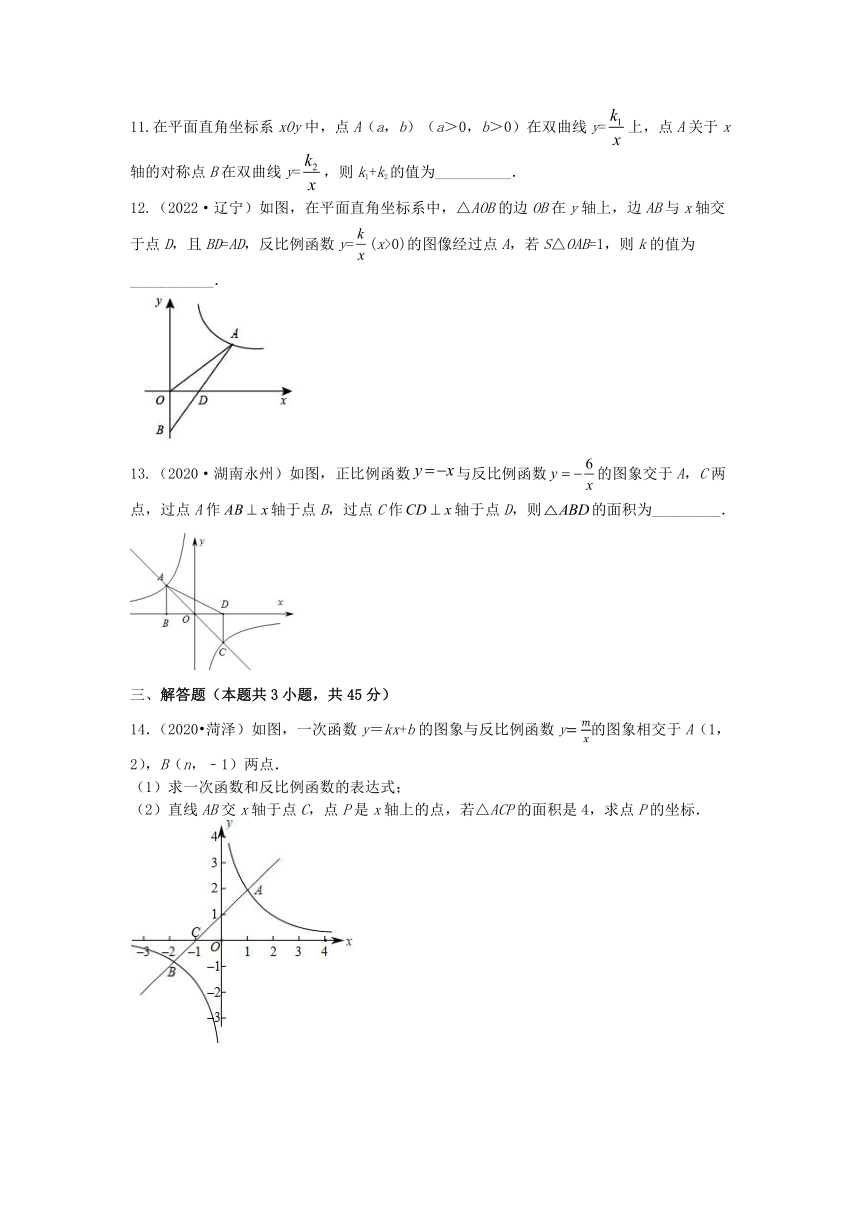
11.在平面直角坐标系xOy中,点A(a,b)(a>0,b>0)在双曲线y=上,点A关于x轴的对称点B在双曲线y=,则k1+k2的值为__________.
12.(2022·辽宁)如图,在平面直角坐标系中,△AOB的边OB在y轴上,边AB与x轴交于点D,且BD=AD,反比例函数y=(x>0)的图像经过点A,若S△OAB=1,则k的值为___________.
13.(2020·湖南永州)如图,正比例函数与反比例函数的图象交于A,C两点,过点A作轴于点B,过点C作轴于点D,则的面积为_________.
解答题(本题共3小题,共45分)
14.(2020 菏泽)如图,一次函数y=kx+b的图象与反比例函数y的图象相交于A(1,2),B(n,﹣1)两点.
(1)求一次函数和反比例函数的表达式;
(2)直线AB交x轴于点C,点P是x轴上的点,若△ACP的面积是4,求点P的坐标.
15.(2020 江西)如图,Rt△ABC中,∠ACB=90°,顶点A,B都在反比例函数y(x>0)的图象上,直线AC⊥x轴,垂足为D,连结OA,OC,并延长OC交AB于点E,当AB=2OA时,点E恰为AB的中点,若∠AOD=45°,OA=2.
(1)求反比例函数的解析式;
(2)求∠EOD的度数.
16.已知双曲线y=(x>0),直线l1:y﹣=k(x﹣)(k<0)过定点F且与双曲线交于A,B两点,设A(x1,y1),B(x2,y2)(x1<x2),直线l2:y=﹣x+.
(1)若k=﹣1,求△OAB的面积S;
(2)若AB=,求k的值;
(3)设N(0,2),P在双曲线上,M在直线l2上且PM∥x轴,求PM+PN最小值,并求PM+PN取得最小值时P的坐标.(参考公式:在平面直角坐标系中,若A(x1,y1),B(x2,y2)则A,B两点间的距离为AB=)
参考答案:
1.C 2.D 3.B 4.C 5.C 6.D 7.A 8.C
9.(2,3)
10.
11.0
12.2
13.6
14.(1)将点A(1,2)代入y,得:m=2,
∴y,
当y=﹣1时,x=﹣2,
∴B(﹣2,﹣1),
将A(1,2)、B(﹣2,﹣1)代入y=kx+b,
得:,
解得,
∴y=x+1;
∴一次函数解析式为y=x+1,反比例函数解析式为y;
(2)在y=x+1中,当y=0时,x+1=0,
解得x=﹣1,
∴C(﹣1,0),
设P(m,0),
则PC=|﹣1﹣m|,
∵S△ACP PC yA=4,
∴|﹣1﹣m|×2=4,
解得m=3或m=﹣5,
∴点P的坐标为(3,0)或(﹣5,0).
15.(1)∵直线AC⊥x轴,垂足为D,∠AOD=45°,
∴△AOD是等腰直角三角形,
∵OA=2,
∴OD=AD=2,
∴A(2,2),
∵顶点A在反比例函数y(x>0)的图象上,
∴k=2×2=4,
∴反比例函数的解析式为y;
(2)∵AB=2OA,点E恰为AB的中点,
∴OA=AE,
∵Rt△ABC中,∠ACB=90°,
∴CE=AE=BE,
∴∠AOE=∠AEO,∠ECB=∠EBC,
∵∠AEO=∠ECB+∠EBC=2∠EBC,
∵BC∥x轴,
∴∠EOD=∠ECB,
∴∠AOE=2∠EOD,
∵∠AOE=45°,
∴∠EOD=15°.
16.解:(1)当k=1时,l1:y=﹣x+2,
联立得,,化简得x2﹣2x+1=0,
解得:x1=﹣1,x2=+1,
设直线l1与y轴交于点C,则C(0,2).
S△OAB=S△AOC﹣S△BOC= 2 (x2﹣x1)=2;
(2)根据题意得: 整理得:kx2+(1﹣k)x﹣1=0(k<0),
∵△=[(1﹣k)]2﹣4×k×(﹣1)=2(1+k2)>0,
∴x1、x2 是方程的两根,
∴ ①,
∴AB==,
=,
=,
将①代入得,AB==(k<0),
∴=,
整理得:2k2+5k+2=0,
解得:k=2,或 k=﹣;
(3)F(,),如图:
设P(x,),则M(﹣+,),
则PM=x+﹣==,
∵PF==,
∴PM=PF.
∴PM+PN=PF+PN≥NF=2,
当点P在NF上时等号成立,此时NF的方程为y=﹣x+2,
由(1)知P(﹣1,+1),
∴当P(﹣1,+1)时,PM+PN最小值是2.
(时间:60分钟 分数:100分)
姓名: 分数:
选择题(本题共8小题,共40分)
1.(2020 金华)已知点(﹣2,a)(2,b)(3,c)在函数y(k>0)的图象上,则下列判断正确的是( )
A.a<b<c B.b<a<c C.a<c<b D.c<b<a
2.(2021·山西)已知反比例函数,则下列描述不正确的是( )
A.图象位于第一,第三象限 B.图象必经过点
C.图象不可能与坐标轴相交 D.随的增大而减小
3.(2020·广西贺州)在反比例函数中,当时,y的值为( )
A.2 B. C. D.
4.(2020 无锡)反比例函数y与一次函数y的图形有一个交点B(,m),则k的值为( )
A.1 B.2 C. D.
5.(2021·广西梧州)如图,在同一平面直角坐标系中,直线y=t(t为常数)与反比例函数y1,y2的图象分别交于点A,B,连接OA,OB,则△OAB的面积为( )
A.5t B. C. D.5
6.(2021·江苏连云港)关于某个函数表达式,甲、乙、丙三位同学都正确地说出了该函数的一个特征.甲:函数图像经过点;乙:函数图像经过第四象限;
丙:当时,y随x的增大而增大.则这个函数表达式可能是( )
A. B. C. D.
7.(2021·辽宁朝阳)如图,O是坐标原点,点B在x轴上,在OAB中,AO=AB=5,OB=6,点A在反比例函数y=(k≠0)图象上,则k的值( )
A.﹣12 B.﹣15 C.﹣20 D.﹣30
8.(2020·西藏)如图,在平面直角坐标系中,直线y=x与反比例函数y=(x>0)的图象交于点A,将直线y=x沿y轴向上平移b个单位长度,交y轴于点B,交反比例函数图象于点C.若OA=2BC,则b的值为( )
A.1 B.2 C.3 D.4
填空题(本题共5小题,每空3分,共15分)
9.(2021·江苏徐州)如图,点分别在函数的图像上,点在轴上.若四边形为正方形,点在第一象限,则的坐标是_____________.
10.(2020·贵州黔南)如图,正方形的边长为10,点A的坐标为,点B在y轴上,若反比例函数的图象过点C,则该反比例函数的解析式为_________.
11.在平面直角坐标系xOy中,点A(a,b)(a>0,b>0)在双曲线y=上,点A关于x轴的对称点B在双曲线y=,则k1+k2的值为__________.
12.(2022·辽宁)如图,在平面直角坐标系中,△AOB的边OB在y轴上,边AB与x轴交于点D,且BD=AD,反比例函数y=(x>0)的图像经过点A,若S△OAB=1,则k的值为___________.
13.(2020·湖南永州)如图,正比例函数与反比例函数的图象交于A,C两点,过点A作轴于点B,过点C作轴于点D,则的面积为_________.
解答题(本题共3小题,共45分)
14.(2020 菏泽)如图,一次函数y=kx+b的图象与反比例函数y的图象相交于A(1,2),B(n,﹣1)两点.
(1)求一次函数和反比例函数的表达式;
(2)直线AB交x轴于点C,点P是x轴上的点,若△ACP的面积是4,求点P的坐标.
15.(2020 江西)如图,Rt△ABC中,∠ACB=90°,顶点A,B都在反比例函数y(x>0)的图象上,直线AC⊥x轴,垂足为D,连结OA,OC,并延长OC交AB于点E,当AB=2OA时,点E恰为AB的中点,若∠AOD=45°,OA=2.
(1)求反比例函数的解析式;
(2)求∠EOD的度数.
16.已知双曲线y=(x>0),直线l1:y﹣=k(x﹣)(k<0)过定点F且与双曲线交于A,B两点,设A(x1,y1),B(x2,y2)(x1<x2),直线l2:y=﹣x+.
(1)若k=﹣1,求△OAB的面积S;
(2)若AB=,求k的值;
(3)设N(0,2),P在双曲线上,M在直线l2上且PM∥x轴,求PM+PN最小值,并求PM+PN取得最小值时P的坐标.(参考公式:在平面直角坐标系中,若A(x1,y1),B(x2,y2)则A,B两点间的距离为AB=)
参考答案:
1.C 2.D 3.B 4.C 5.C 6.D 7.A 8.C
9.(2,3)
10.
11.0
12.2
13.6
14.(1)将点A(1,2)代入y,得:m=2,
∴y,
当y=﹣1时,x=﹣2,
∴B(﹣2,﹣1),
将A(1,2)、B(﹣2,﹣1)代入y=kx+b,
得:,
解得,
∴y=x+1;
∴一次函数解析式为y=x+1,反比例函数解析式为y;
(2)在y=x+1中,当y=0时,x+1=0,
解得x=﹣1,
∴C(﹣1,0),
设P(m,0),
则PC=|﹣1﹣m|,
∵S△ACP PC yA=4,
∴|﹣1﹣m|×2=4,
解得m=3或m=﹣5,
∴点P的坐标为(3,0)或(﹣5,0).
15.(1)∵直线AC⊥x轴,垂足为D,∠AOD=45°,
∴△AOD是等腰直角三角形,
∵OA=2,
∴OD=AD=2,
∴A(2,2),
∵顶点A在反比例函数y(x>0)的图象上,
∴k=2×2=4,
∴反比例函数的解析式为y;
(2)∵AB=2OA,点E恰为AB的中点,
∴OA=AE,
∵Rt△ABC中,∠ACB=90°,
∴CE=AE=BE,
∴∠AOE=∠AEO,∠ECB=∠EBC,
∵∠AEO=∠ECB+∠EBC=2∠EBC,
∵BC∥x轴,
∴∠EOD=∠ECB,
∴∠AOE=2∠EOD,
∵∠AOE=45°,
∴∠EOD=15°.
16.解:(1)当k=1时,l1:y=﹣x+2,
联立得,,化简得x2﹣2x+1=0,
解得:x1=﹣1,x2=+1,
设直线l1与y轴交于点C,则C(0,2).
S△OAB=S△AOC﹣S△BOC= 2 (x2﹣x1)=2;
(2)根据题意得: 整理得:kx2+(1﹣k)x﹣1=0(k<0),
∵△=[(1﹣k)]2﹣4×k×(﹣1)=2(1+k2)>0,
∴x1、x2 是方程的两根,
∴ ①,
∴AB==,
=,
=,
将①代入得,AB==(k<0),
∴=,
整理得:2k2+5k+2=0,
解得:k=2,或 k=﹣;
(3)F(,),如图:
设P(x,),则M(﹣+,),
则PM=x+﹣==,
∵PF==,
∴PM=PF.
∴PM+PN=PF+PN≥NF=2,
当点P在NF上时等号成立,此时NF的方程为y=﹣x+2,
由(1)知P(﹣1,+1),
∴当P(﹣1,+1)时,PM+PN最小值是2.
同课章节目录
