2023年九年级数学中考复习 二次函数与等腰三角形综合压轴题 考前冲刺达标测评(含答案)
文档属性
| 名称 | 2023年九年级数学中考复习 二次函数与等腰三角形综合压轴题 考前冲刺达标测评(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 710.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-07 00:00:00 | ||
图片预览


文档简介
2023年春九年级数学中考复习《二次函数与等腰三角形综合压轴题》
考前冲刺达标测评(附答案)
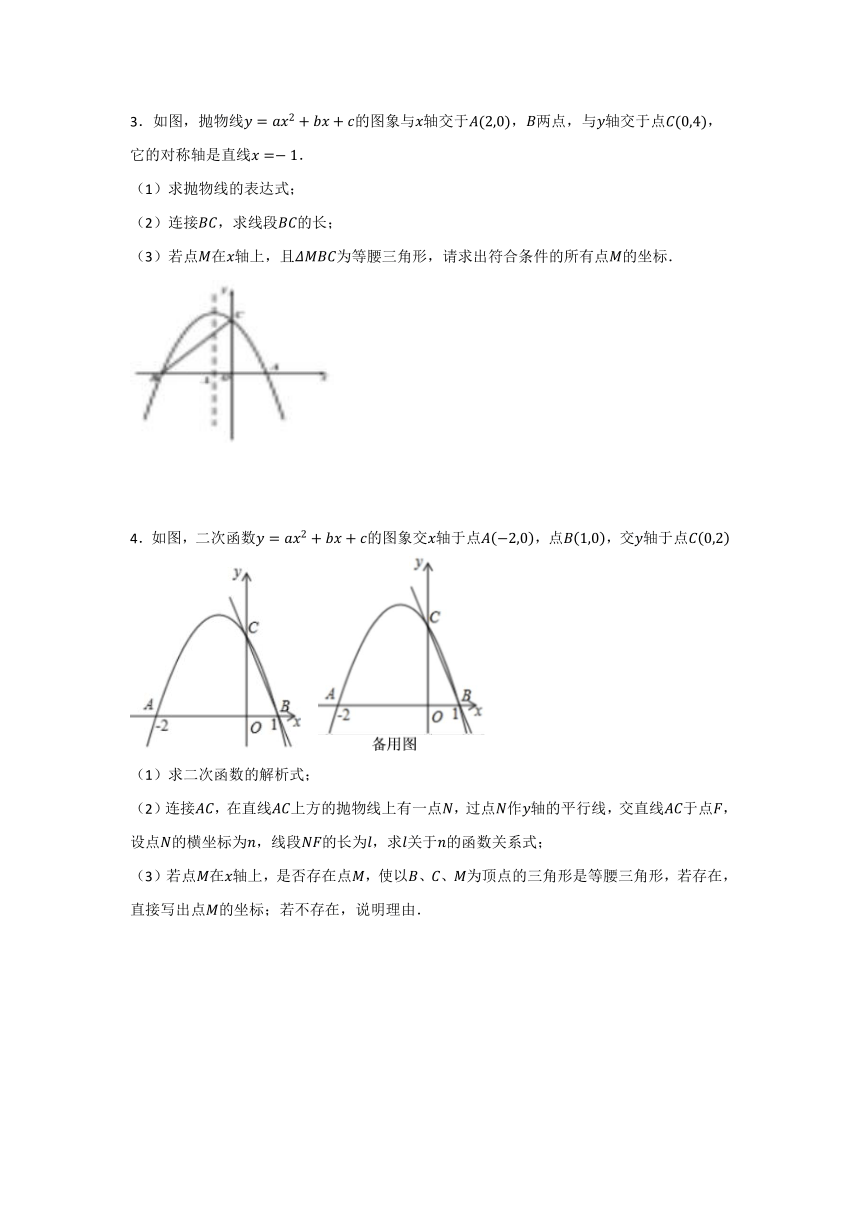
1.如图,抛物线与轴交于点和点,并经过点,抛物线的顶点为.将抛物线平移后得到顶点为且对称轴为直线的抛物线.
(1)求抛物线的表达式;
(2)在直线上是否存在点,使为等腰三角形?若存在,请求出所有点的坐标;若不存在,请说明理由.
2.如图1,已知抛物线与轴交于点,与轴交于点.
(1)求,的值;
(2)点是第一象限抛物线上一动点,过点作轴的垂线,交于点.当△为等腰三角形时,求点的坐标;
(3)如图2,抛物线顶点为,已知直线与二次函数图象相交于,两点.求证:无论为何值,△恒为直角三角形.
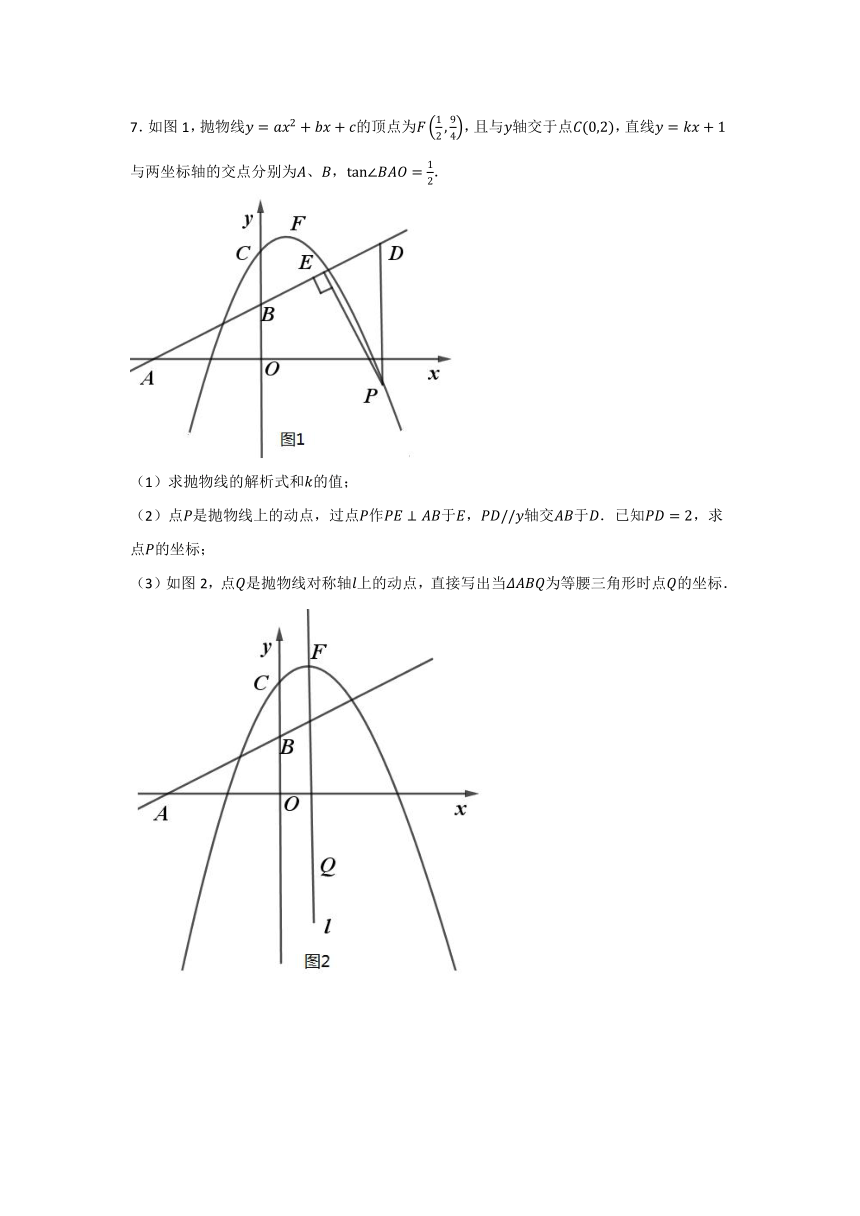
3.如图,抛物线的图象与轴交于,两点,与轴交于点,它的对称轴是直线.
(1)求抛物线的表达式;
(2)连接,求线段的长;
(3)若点在轴上,且为等腰三角形,请求出符合条件的所有点的坐标.
4.如图,二次函数的图象交轴于点,点,交轴于点
(1)求二次函数的解析式;
(2)连接,在直线上方的抛物线上有一点,过点作轴的平行线,交直线于点,设点的横坐标为,线段的长为,求关于的函数关系式;
(3)若点在轴上,是否存在点,使以、、为顶点的三角形是等腰三角形,若存在,直接写出点的坐标;若不存在,说明理由.
5.如图,在平面直角坐标系中,已知的直角顶点,斜边在轴上,且点的坐标为,点是的中点,点是边上的一个动点,抛物线过,,三点.
(1)当时,
①求抛物线的解析式;
②平行于对称轴的直线与轴,,分别交于点,,,若以点,,为顶点的三角形与相似,求点的值.
(2)以为等腰三角形顶角顶点,为腰构造等腰,且点落在轴上.若在轴上满足条件的点有且只有一个时,请直接写出点的坐标.
6.如图①,点G是等边三角形AOB的外心,点A在第一象限,点B坐标为(4,0),连结OG.抛物线y=ax(x﹣2)+1+的顶点为P.
(1)直接写出点A的坐标与抛物线的对称轴;
(2)连结OP,求当∠AOG=2∠AOP时a的值.
(3)如图②,若抛物线开口向上,点C,D分别为抛物线和线段AB上的动点,以CD为底边构造顶角为120°的等腰三角形CDE(点C,D,E成逆时针顺序),连结GE.
①点Q在x轴上,当四边形GDQO为平行四边形时,求GQ的值;
②当GE的最小值为1时,求抛物线的解析式.
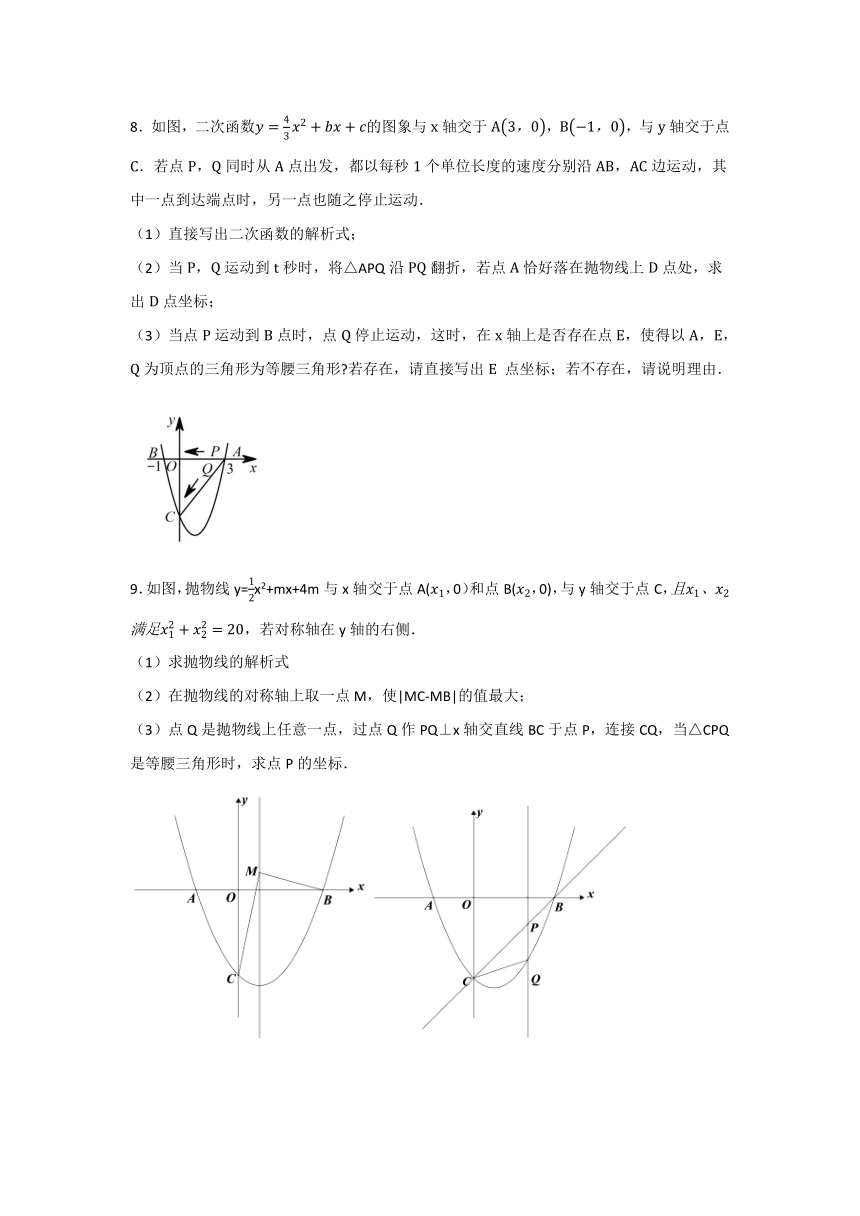
7.如图1,抛物线的顶点为,且与轴交于点,直线与两坐标轴的交点分别为、,.
(1)求抛物线的解析式和的值;
(2)点是抛物线上的动点,过点作于,轴交于.已知,求点的坐标;
(3)如图2,点是抛物线对称轴上的动点,直接写出当为等腰三角形时点的坐标.
8.如图,二次函数的图象与轴交于,,与轴交于点.若点,同时从点出发,都以每秒个单位长度的速度分别沿,边运动,其中一点到达端点时,另一点也随之停止运动.
(1)直接写出二次函数的解析式;
(2)当,运动到秒时,将△APQ沿翻折,若点恰好落在抛物线上点处,求出点坐标;
(3)当点运动到点时,点停止运动,这时,在轴上是否存在点,使得以,,为顶点的三角形为等腰三角形 若存在,请直接写出 点坐标;若不存在,请说明理由.
9.如图,抛物线y=x2+mx+4m与x轴交于点A(,0)和点B(,0),与y轴交于点C,,若对称轴在y轴的右侧.
(1)求抛物线的解析式
(2)在抛物线的对称轴上取一点M,使|MC-MB|的值最大;
(3)点Q是抛物线上任意一点,过点Q作PQ⊥x轴交直线BC于点P,连接CQ,当△CPQ是等腰三角形时,求点P的坐标.
10.如图,二次函数的图象与y轴交于点A(0,-4),与x轴交于点B(-2,0),C(8,0),连接AB,AC.
(1)求出二次函数表达式;
(2)若点N在线段BC上运动(不与点B,C重合),过点N作NM∥AB,交AC于点M,连接AN,当以点A,M,N为顶点的三角形与以点A,B,O为顶点的三角形相似时,求此时点N的坐标;
(3)若点N在x轴上运动,当以点A,N,C为顶点的三角形是等腰三角形时,请直接写出此时点N的坐标.
11.如图,已知抛物线,将抛物线平移后经过点,得到抛物线,与轴交于点;
(1)求抛物线的解析式;
(2)判断的形状,并说明理由;
(3)点为抛物线上的动点,过点作轴,与抛物线交于点,是否存在点,满足?若存在,求出点的坐标;若不存在,说明理由.
12.如图,在平面直角坐标系中,点A的坐标为(6,),AB⊥x轴于点B,AC⊥y轴于点C,连接BC.点D是线段AC的中点,点E的坐标为(0,),点F是线段EO上的一个动点.过点A,D,F的抛物线与x轴正半轴交于点G,连接DG交线段AB于点M.
(1)求∠ACB的度数;
(2)当点F运动到原点时,求过A,D,F三点的抛物线的函数表达式及点G的坐标;
(3)以线段DM为一边作等边三角形DMP,点P与点A在直线DG同侧,当点F从点E运动到点O时,请直接写出点P运动的路径的长.
参考答案
1.解:(1)由于抛物线经过点和点,所以,
解得,抛物线.
当时,,解得,,所以点坐标为,
因为抛物线由抛物线平移得到,且顶点为,
所以抛物线的表达式为.
(2)在直线上存在点,使是等腰三角形.
由于,所以点坐标为,
根据勾股定理,设点坐标为,
分三种情况:
①当时,,解得,此时点坐标为;
②当时,,,此时点坐标为或;
③当时,,解得或(舍去),此时点坐标为.
综上,是等腰三角形时,点坐标为或或或.
2.解:(1)将点代入,
得,
解得,
∴;
(2)设直线的解析式为,
将点代入,
得,,
∴直线的解析式为,
设点,则点 ,
过点作于点,
①当时,,
∵,
∴,
∵,
∴,
∴,
∴,
即,
解得,(舍去),,
∴;
②当时,
,
解得
∴
③当时,此时点P和点M重合
,
解得
∴
综上所述点的坐标,,;
(3)将二次函数与直线的表达式联立并整理得:,
设点的坐标为,
则,
则 ,
同理:,
点的坐标为,,点,
∴
即:为直角三角形.
3.解:(1)根据题意得:,
解得:,
∴抛物线的解析式为:;
(2)∵点的坐标为,对称轴是直线,
∴,
∴,
∵,
∴,
∴;
(3)设,
∵,,
∴,
是等腰三角形,分三种情况;
①当时,,解得,
∴;
②当时,由(2)知,
则,
解得,
∴或;
③当时,由(2)知,
则,
解得或(舍)
∴.
综上可知,符合条件的所有点的坐标为:或或或.
4.解:(1)∵二次函数y=ax2+bx+c的图象交x轴于A(-2,0),B(1,0),
设二次函数的解析式为:y=a(x+2)(x-1),
把C(0,2)代入得:2=a(0+2)(0-1),
a=-1,
∴y=-(x+2)(x-1)=-x2-x+2,
故抛物线的表达式为:y=-x2-x+2;
(2)设直线AC的解析式为:y=kx+b,
把A(-2,0)、C(0,2)代入得: ,
解得: ,
∴直线AC的解析式为:y=x+2,
设点N(n,-n2-n+2),则点F(n,n+2),
l=-n2-n+2-(n+2)=-n2-2n;
(3)存在,分三种情况:
①如图2,当BC=CM1时,M1(-1,0);
②如图2,由勾股定理得:BC= ,
以B为圆心,以BC为半径画圆,交x轴于M2、M3,则BC=BM2=BM3=,
此时,M2(1-,0),M3(1+,0);
③如图3,作BC的中垂线,交x轴于M4,连接CM4,则CM4=BM4,
设OM4=x,则CM4=BM4=x+1,
由勾股定理得:22+x2=(1+x)2,
解得:x=,
∵M4在x轴的负半轴上,
∴M4(-,0),
综上,点M的坐标为:(-1,0)或(1+,0)或(1-,0)或(-,0).
5.解:(1)①∵点,点,
∴,,
在中,,
∵点是的中点,
∴点的坐标为,,
∵,
∴,
∴,即,
∴,
∴的坐标为,即,
把和D代入,
得,
解得,
∴抛物线的解析式为.
②当时,可得,
解得,
∴;
当时,可得,
解得,
∴.
综上所述,的值为或0.
(2)若在轴上满足条件的点有且只有一个,则有两种情况,
第一种情况,EG⊥AB,如图,
∠A+∠B=90°,∠B+∠BCO=90°,∠B+∠BEG=90°,
∴∠A=∠BCO=∠BEG,
∴△AOC∽△COB,△AOC∽△COB,
∴,,
∴,即,
,即,
设,则,,
在直角三角形CDE中,,
∴,
解得或(舍),
,
由,得,,
∴,
∴E点坐标为,
第二种情况如图,以E为圆心DE为半径作圆,交AB延长线于M,过E作EH⊥AB于H, D、E、M三点共线时,
则E为DM的中点,
由D可知E的纵坐标为3,即EH=3,
由题可知△EHB∽△COB,
∴即,
∴HB=4,OH=OB-HB=16-4=12,
∴E点坐标为,
∴答案为或.
6.解:(1)如图,连接AG并延长AG交OB于H,
∵点B坐标为(4,0),
∴OB=4,
∵点G是等边三角形AOB的外心,
∴AH⊥OB,OA=OB=4,∠AOB=60°,
∴∠OAH=30°,
∴OH=OA=2,AH=OH=2,
∴点A(2,2),
∵抛物线y=ax(x﹣2)+1+=ax2﹣2ax+1+,
∴对称轴为:直线x=﹣=1;
(2)如图,过点P作PN⊥OB于N,交AO于F,
∴ON=1,
∵点G是等边三角形AOB的外心,
∴OG平分∠AOB,
∴∠AOG=30°=∠BOG,
当点P在△AOB内,
∵∠AOG=2∠AOP,
∴∠AOP=15°=∠POG,
∴∠PON=45°,
∵PN⊥OB,
∴∠PON=∠OPN=45°,
∴PN=ON=1,
∴点P坐标(1,1),
∴1=a(1﹣2)+1+,
∴a=,
当点P在△AOB外,
同理可得∠AOP'=15°,
∴∠P'ON=75°,
∴∠OP'N=15°=∠AOP',
∴OF=P'F,
∵∠AOB=60°,P'N⊥OB,
∴OF=2ON=2=P'F,FN=ON=,
∴P'N=P'F+FN=2+,
∴点P坐标为(1,2+),
∴2+=a(1﹣2)+1+,
∴a=﹣1,
综上所述:a=﹣1或;
(3)如图,连接AG并延长AG交OB于H,
∵点G是等边三角形AOB的外心,
∴AG=2GH,OH=BH=2,AH=2,
∴GH=,
∵四边形GDQO为平行四边形,
∴GD∥OB,GD=OQ,
∴,
∴GD=,
∴QH=,
∴GQ===;
②如图,在OB上截取OM=BD,连接CM,GM,GB,MD,GD,
∵点G是等边三角形AOB的外心,
∴OG=GB,∠GOB=∠GBO=∠ABG=30°,
又∵OM=BD,
∴△OGM≌△BGD(SAS),
∴MG=GD,∠OGM=∠BGD,
∴∠OGB=∠MGD=180°﹣30°﹣30°=120°,
∴MD=GD,∠GDM=30°,
∵△CDE中CE=DE,∠CED=120°,
∴CD=DE,∠CDE=30°,
∴∠MDC=∠GDE,,
∴△GDE∽△MDC,
∴=,
当GE最小值为1时,MC最小值为,
∴当点C与抛物线顶点P重合,且CM⊥OB时,CM有最小值,
∴CM的最小值为顶点P的纵坐标,
∴点P坐标(1,),
∴=a(1﹣2)+1+,
∴a=1,
∴抛物线的解析式为:y=x(x﹣2)+1+=(x﹣1)2+.
7.解:(1)因为抛物线的顶点为,所以设抛物线的关系式是,
把点C的坐标(0,2)代入,得,C的坐标(0,2)
解得,
∴,
把代入,
得,
∴点B的坐标(0,1),
∴OB=1,
∵,
∴,
∴点A的坐标(-2,0),
把(-2,0)代入,得,
∴;
(2)由(1)知直线的关系式:,
设点的横坐标为,
则点的纵坐标为,点的坐标为 (,),
,
∴,
当时,解得:,;
当,即时,
∵,
∴方程无实数根;
当时,;
当时,
∴P (2,0)或P (,);
(3)∵抛物线的对称轴为,
∴设点点Q的坐标(,),
∵点A的坐标(-2,0),点B的坐标(0,1),
∴,
①当时,
,即,
解得,即,
∴、;
②当时,
过Q作QE⊥AB于E,过E作EG⊥轴于G,
∴E为AB的中点,G为AO的中点,
∴AG=AO=1,
∵,则,
∴EG=,
∴点E的坐标为(-1,),
∵,,
∴,
∴,则,
∴NG=,则NO=1-,
∴点N的坐标为(,),
设直线QE的解析式为,
则,
解得:,
∴直线QE的解析式为,
把代入,得;
∴
③∵,
∴.
综上所述,符合条件的点为:、、.
8.解:(1)将,代入,求得,
∴;
(2)如图,D点关于PQ与A点对称,过点Q作于
∵,,
∴
∴四边形为菱形
∵
∴
∴
∴,
∴
∵
∴
∵D在二次函数上
∴
∴,或(舍去)
∴;
(3)存在满足条件的点E,点E的坐标为或或或
如上图,过点Q作于D,此时
∵,,,
∴,,
∴,
∵
∴
∴
∴,;
①如下图,作AQ的垂直平分线,交AQ于E
此时,即为等腰三角形
设,则,
∴在中,,解得
∴
∴;
②如下图,以Q为圆心,AQ长半径画圆,交x轴于E
此时
∵
∴
∴
∴;
③当时
1)当E在A点左边时
∵
∴
2)当E在A点右边时
∵
∴;
综上所述,存在满足条件的点E,点E的坐标为或或或.
9.解:(1)∵y=x2+mx+4m与x轴交于,0)和点B(,0),
∴是方程x2+mx+4m=0的两个根,
,
,
∴(-2m)2-16m=20,
解得m1=5,m2=-1,
∵对称轴在y轴的右侧,
∴m=-1,
∴y=-x-4;
(2)y=-x-4中,当x=0时,y=-4,
当y=0时=-2,=4,
∴A(-2,0),B(4,0),C(0,-4),
过点AC作直线交对称轴于点M,
设直线AC的解析式为y=kx+b,
将(-2,0),(0,-4)代入,
则,
解得,
得y=-2x-4,当x=1时,y=-6,
∴M(1,-6);
(3)直线BC的解析式为y=k1x+b1,
将(4,0),(0,-4)代入,
则,
解得,
得y=x-4,
∴∠OCB=∠OBC=45°,
设P的横坐标为x,作PH⊥y轴于H,
则PC=,
∴PQ=|(x-4)--x-4)|
(图一) (图二)
如图一图二,当CQ=CP时,(x-4)+-x-4)=-8,
x=0,不合题意,所以不存在;
(图三) (图四) (图五)
如图三,当PC=PQ时,=(x-4)- -x-4),
解得x=,
∴P()
如图四,当CQ=PQ时,x=(x-4)- -x-4),
解得x=2,
∴P(2,-2);
如图五,当PC=PQ时 ,
-x-4)-(x-4)=,
解得:x=,
∴P();
综上:P1() ,P2(2,-2),P3().
10.解:(1)∵二次函数的图象与x轴交于点B(-2,0)、C(8,0),与y轴交于A(0,-4)
∴ ,
解得: ,
∴二次函数表达式是;
(2)∵AB2=BO2+AO2=20,AC2=AO2+OC2=80.
∵BC2=(BO+OC)2=100,
∴AB2+AC2=BC2.
∴△ABC是直角三角形;
设点N的坐标为(n,0),
∵∠AOB=∠NMA=90°,
∴有两种情况:
①当时,
∵,
∴
∴
∴=8-n
Rt△OAN中,
即
解得:n=3
∴n(3,0)
②当时,
∵NM∥AB
∴
∴
即N与原点O重合,
∴此时N(0,0)
综合①②得,N点坐标是(3,0)或(0,0).
(3)由(2)知,AC=,
①以A为圆心,以AC长为半径作圆,交x轴于N,此时N的坐标为( 8,0),
②以C为圆心,以AC长为半径作圆,交x轴于N,此时N的坐标为(,0)或(8+4,0);
③如图,作AC的垂直平分线交AC于M,交x轴于N,
∴△AOC∽△NMC.
∴,即,
∴CN=5.
∴此时N的坐标为(3,0),
综上,若点N在x轴上运动,当以点A、N、C为顶点的三角形是等腰三角形时,点N的坐标分别为(-8,0)、(8-4,0)、(3,0)、(8+4,0).
11.解:(1)设抛物线的解析式为,
经过点、,
根据题意得,
解得
所以抛物线的解析式为.
(2)的形状是等腰三角形.
理由:根据题意得,,.
∵,,,
∴,即的形状是等腰三角形.
(3)存在,理由:
设,
根据题意,得.
∵
∴,解得,
∴,.
12.解:(1)∵点A的坐标为,AB⊥x轴于点B,
∴B(6,0),
∴AB=,
∵点A的坐标为,AC⊥y轴于点C,
∴C(0,),
∴AC=6,
∵AB⊥x轴,AC⊥y轴,
∴∠ABO=∠ACO=90°=∠BOC,
∴四边形OBAC是矩形,
∴∠BAC=90°,
在Rt△ABC中,tan∠ACB=,
∴∠ACB=60°;
(2)由(1)知,C(0,),
∵点D是AC的中点,
∴D(3,),
设抛物线的解析式为y=ax2+bx+c,
将点A(6,),D(3,),O(0,0)代入抛物线解析式中,得,
∴,
∴抛物线的解析式为,
令y=0,则,
∴x=0或x=9,
∴G(9,0);
(3)如图,
当点F从点E运动到点O时,点M的运动轨迹是线段MM',
∴以DM为边的等边三角形的顶点P的轨迹是线段PP',
当抛物线过原点时,DG与AB的交点记作点M,当抛物线过点E时,DG'与AB的交点为M',
∵△DMP是等边三角形,
∴DM=DP,∠MDP=60°,
∵△DM'P'是等边三角形
∴DM'=DP',∠M'DP'=60°,
∴∠MDM'=∠PDP',
∴△MDM'≌△PDP'(SAS),
∴PP'=MM',
由(2)知,G(9,0),
∵D(3,),
∴直线DG的解析式,
令x=6,则y=,
∴M,
当抛物线过点E时,即抛物线过点A,D,E,
设抛物线的解析式为,
∴,
∴,
∴过点A,D,E的抛物线的解析式为,
令y=0,则,
∴x=﹣3或x=12,
∴G'(12,0),
∴DG'的解析式为,
令x=6,则y=,
∴M'(6,),
∴PP'=MM'=,
即点P运动的路径的长为.
考前冲刺达标测评(附答案)
1.如图,抛物线与轴交于点和点,并经过点,抛物线的顶点为.将抛物线平移后得到顶点为且对称轴为直线的抛物线.
(1)求抛物线的表达式;
(2)在直线上是否存在点,使为等腰三角形?若存在,请求出所有点的坐标;若不存在,请说明理由.
2.如图1,已知抛物线与轴交于点,与轴交于点.
(1)求,的值;
(2)点是第一象限抛物线上一动点,过点作轴的垂线,交于点.当△为等腰三角形时,求点的坐标;
(3)如图2,抛物线顶点为,已知直线与二次函数图象相交于,两点.求证:无论为何值,△恒为直角三角形.
3.如图,抛物线的图象与轴交于,两点,与轴交于点,它的对称轴是直线.
(1)求抛物线的表达式;
(2)连接,求线段的长;
(3)若点在轴上,且为等腰三角形,请求出符合条件的所有点的坐标.
4.如图,二次函数的图象交轴于点,点,交轴于点
(1)求二次函数的解析式;
(2)连接,在直线上方的抛物线上有一点,过点作轴的平行线,交直线于点,设点的横坐标为,线段的长为,求关于的函数关系式;
(3)若点在轴上,是否存在点,使以、、为顶点的三角形是等腰三角形,若存在,直接写出点的坐标;若不存在,说明理由.
5.如图,在平面直角坐标系中,已知的直角顶点,斜边在轴上,且点的坐标为,点是的中点,点是边上的一个动点,抛物线过,,三点.
(1)当时,
①求抛物线的解析式;
②平行于对称轴的直线与轴,,分别交于点,,,若以点,,为顶点的三角形与相似,求点的值.
(2)以为等腰三角形顶角顶点,为腰构造等腰,且点落在轴上.若在轴上满足条件的点有且只有一个时,请直接写出点的坐标.
6.如图①,点G是等边三角形AOB的外心,点A在第一象限,点B坐标为(4,0),连结OG.抛物线y=ax(x﹣2)+1+的顶点为P.
(1)直接写出点A的坐标与抛物线的对称轴;
(2)连结OP,求当∠AOG=2∠AOP时a的值.
(3)如图②,若抛物线开口向上,点C,D分别为抛物线和线段AB上的动点,以CD为底边构造顶角为120°的等腰三角形CDE(点C,D,E成逆时针顺序),连结GE.
①点Q在x轴上,当四边形GDQO为平行四边形时,求GQ的值;
②当GE的最小值为1时,求抛物线的解析式.
7.如图1,抛物线的顶点为,且与轴交于点,直线与两坐标轴的交点分别为、,.
(1)求抛物线的解析式和的值;
(2)点是抛物线上的动点,过点作于,轴交于.已知,求点的坐标;
(3)如图2,点是抛物线对称轴上的动点,直接写出当为等腰三角形时点的坐标.
8.如图,二次函数的图象与轴交于,,与轴交于点.若点,同时从点出发,都以每秒个单位长度的速度分别沿,边运动,其中一点到达端点时,另一点也随之停止运动.
(1)直接写出二次函数的解析式;
(2)当,运动到秒时,将△APQ沿翻折,若点恰好落在抛物线上点处,求出点坐标;
(3)当点运动到点时,点停止运动,这时,在轴上是否存在点,使得以,,为顶点的三角形为等腰三角形 若存在,请直接写出 点坐标;若不存在,请说明理由.
9.如图,抛物线y=x2+mx+4m与x轴交于点A(,0)和点B(,0),与y轴交于点C,,若对称轴在y轴的右侧.
(1)求抛物线的解析式
(2)在抛物线的对称轴上取一点M,使|MC-MB|的值最大;
(3)点Q是抛物线上任意一点,过点Q作PQ⊥x轴交直线BC于点P,连接CQ,当△CPQ是等腰三角形时,求点P的坐标.
10.如图,二次函数的图象与y轴交于点A(0,-4),与x轴交于点B(-2,0),C(8,0),连接AB,AC.
(1)求出二次函数表达式;
(2)若点N在线段BC上运动(不与点B,C重合),过点N作NM∥AB,交AC于点M,连接AN,当以点A,M,N为顶点的三角形与以点A,B,O为顶点的三角形相似时,求此时点N的坐标;
(3)若点N在x轴上运动,当以点A,N,C为顶点的三角形是等腰三角形时,请直接写出此时点N的坐标.
11.如图,已知抛物线,将抛物线平移后经过点,得到抛物线,与轴交于点;
(1)求抛物线的解析式;
(2)判断的形状,并说明理由;
(3)点为抛物线上的动点,过点作轴,与抛物线交于点,是否存在点,满足?若存在,求出点的坐标;若不存在,说明理由.
12.如图,在平面直角坐标系中,点A的坐标为(6,),AB⊥x轴于点B,AC⊥y轴于点C,连接BC.点D是线段AC的中点,点E的坐标为(0,),点F是线段EO上的一个动点.过点A,D,F的抛物线与x轴正半轴交于点G,连接DG交线段AB于点M.
(1)求∠ACB的度数;
(2)当点F运动到原点时,求过A,D,F三点的抛物线的函数表达式及点G的坐标;
(3)以线段DM为一边作等边三角形DMP,点P与点A在直线DG同侧,当点F从点E运动到点O时,请直接写出点P运动的路径的长.
参考答案
1.解:(1)由于抛物线经过点和点,所以,
解得,抛物线.
当时,,解得,,所以点坐标为,
因为抛物线由抛物线平移得到,且顶点为,
所以抛物线的表达式为.
(2)在直线上存在点,使是等腰三角形.
由于,所以点坐标为,
根据勾股定理,设点坐标为,
分三种情况:
①当时,,解得,此时点坐标为;
②当时,,,此时点坐标为或;
③当时,,解得或(舍去),此时点坐标为.
综上,是等腰三角形时,点坐标为或或或.
2.解:(1)将点代入,
得,
解得,
∴;
(2)设直线的解析式为,
将点代入,
得,,
∴直线的解析式为,
设点,则点 ,
过点作于点,
①当时,,
∵,
∴,
∵,
∴,
∴,
∴,
即,
解得,(舍去),,
∴;
②当时,
,
解得
∴
③当时,此时点P和点M重合
,
解得
∴
综上所述点的坐标,,;
(3)将二次函数与直线的表达式联立并整理得:,
设点的坐标为,
则,
则 ,
同理:,
点的坐标为,,点,
∴
即:为直角三角形.
3.解:(1)根据题意得:,
解得:,
∴抛物线的解析式为:;
(2)∵点的坐标为,对称轴是直线,
∴,
∴,
∵,
∴,
∴;
(3)设,
∵,,
∴,
是等腰三角形,分三种情况;
①当时,,解得,
∴;
②当时,由(2)知,
则,
解得,
∴或;
③当时,由(2)知,
则,
解得或(舍)
∴.
综上可知,符合条件的所有点的坐标为:或或或.
4.解:(1)∵二次函数y=ax2+bx+c的图象交x轴于A(-2,0),B(1,0),
设二次函数的解析式为:y=a(x+2)(x-1),
把C(0,2)代入得:2=a(0+2)(0-1),
a=-1,
∴y=-(x+2)(x-1)=-x2-x+2,
故抛物线的表达式为:y=-x2-x+2;
(2)设直线AC的解析式为:y=kx+b,
把A(-2,0)、C(0,2)代入得: ,
解得: ,
∴直线AC的解析式为:y=x+2,
设点N(n,-n2-n+2),则点F(n,n+2),
l=-n2-n+2-(n+2)=-n2-2n;
(3)存在,分三种情况:
①如图2,当BC=CM1时,M1(-1,0);
②如图2,由勾股定理得:BC= ,
以B为圆心,以BC为半径画圆,交x轴于M2、M3,则BC=BM2=BM3=,
此时,M2(1-,0),M3(1+,0);
③如图3,作BC的中垂线,交x轴于M4,连接CM4,则CM4=BM4,
设OM4=x,则CM4=BM4=x+1,
由勾股定理得:22+x2=(1+x)2,
解得:x=,
∵M4在x轴的负半轴上,
∴M4(-,0),
综上,点M的坐标为:(-1,0)或(1+,0)或(1-,0)或(-,0).
5.解:(1)①∵点,点,
∴,,
在中,,
∵点是的中点,
∴点的坐标为,,
∵,
∴,
∴,即,
∴,
∴的坐标为,即,
把和D代入,
得,
解得,
∴抛物线的解析式为.
②当时,可得,
解得,
∴;
当时,可得,
解得,
∴.
综上所述,的值为或0.
(2)若在轴上满足条件的点有且只有一个,则有两种情况,
第一种情况,EG⊥AB,如图,
∠A+∠B=90°,∠B+∠BCO=90°,∠B+∠BEG=90°,
∴∠A=∠BCO=∠BEG,
∴△AOC∽△COB,△AOC∽△COB,
∴,,
∴,即,
,即,
设,则,,
在直角三角形CDE中,,
∴,
解得或(舍),
,
由,得,,
∴,
∴E点坐标为,
第二种情况如图,以E为圆心DE为半径作圆,交AB延长线于M,过E作EH⊥AB于H, D、E、M三点共线时,
则E为DM的中点,
由D可知E的纵坐标为3,即EH=3,
由题可知△EHB∽△COB,
∴即,
∴HB=4,OH=OB-HB=16-4=12,
∴E点坐标为,
∴答案为或.
6.解:(1)如图,连接AG并延长AG交OB于H,
∵点B坐标为(4,0),
∴OB=4,
∵点G是等边三角形AOB的外心,
∴AH⊥OB,OA=OB=4,∠AOB=60°,
∴∠OAH=30°,
∴OH=OA=2,AH=OH=2,
∴点A(2,2),
∵抛物线y=ax(x﹣2)+1+=ax2﹣2ax+1+,
∴对称轴为:直线x=﹣=1;
(2)如图,过点P作PN⊥OB于N,交AO于F,
∴ON=1,
∵点G是等边三角形AOB的外心,
∴OG平分∠AOB,
∴∠AOG=30°=∠BOG,
当点P在△AOB内,
∵∠AOG=2∠AOP,
∴∠AOP=15°=∠POG,
∴∠PON=45°,
∵PN⊥OB,
∴∠PON=∠OPN=45°,
∴PN=ON=1,
∴点P坐标(1,1),
∴1=a(1﹣2)+1+,
∴a=,
当点P在△AOB外,
同理可得∠AOP'=15°,
∴∠P'ON=75°,
∴∠OP'N=15°=∠AOP',
∴OF=P'F,
∵∠AOB=60°,P'N⊥OB,
∴OF=2ON=2=P'F,FN=ON=,
∴P'N=P'F+FN=2+,
∴点P坐标为(1,2+),
∴2+=a(1﹣2)+1+,
∴a=﹣1,
综上所述:a=﹣1或;
(3)如图,连接AG并延长AG交OB于H,
∵点G是等边三角形AOB的外心,
∴AG=2GH,OH=BH=2,AH=2,
∴GH=,
∵四边形GDQO为平行四边形,
∴GD∥OB,GD=OQ,
∴,
∴GD=,
∴QH=,
∴GQ===;
②如图,在OB上截取OM=BD,连接CM,GM,GB,MD,GD,
∵点G是等边三角形AOB的外心,
∴OG=GB,∠GOB=∠GBO=∠ABG=30°,
又∵OM=BD,
∴△OGM≌△BGD(SAS),
∴MG=GD,∠OGM=∠BGD,
∴∠OGB=∠MGD=180°﹣30°﹣30°=120°,
∴MD=GD,∠GDM=30°,
∵△CDE中CE=DE,∠CED=120°,
∴CD=DE,∠CDE=30°,
∴∠MDC=∠GDE,,
∴△GDE∽△MDC,
∴=,
当GE最小值为1时,MC最小值为,
∴当点C与抛物线顶点P重合,且CM⊥OB时,CM有最小值,
∴CM的最小值为顶点P的纵坐标,
∴点P坐标(1,),
∴=a(1﹣2)+1+,
∴a=1,
∴抛物线的解析式为:y=x(x﹣2)+1+=(x﹣1)2+.
7.解:(1)因为抛物线的顶点为,所以设抛物线的关系式是,
把点C的坐标(0,2)代入,得,C的坐标(0,2)
解得,
∴,
把代入,
得,
∴点B的坐标(0,1),
∴OB=1,
∵,
∴,
∴点A的坐标(-2,0),
把(-2,0)代入,得,
∴;
(2)由(1)知直线的关系式:,
设点的横坐标为,
则点的纵坐标为,点的坐标为 (,),
,
∴,
当时,解得:,;
当,即时,
∵,
∴方程无实数根;
当时,;
当时,
∴P (2,0)或P (,);
(3)∵抛物线的对称轴为,
∴设点点Q的坐标(,),
∵点A的坐标(-2,0),点B的坐标(0,1),
∴,
①当时,
,即,
解得,即,
∴、;
②当时,
过Q作QE⊥AB于E,过E作EG⊥轴于G,
∴E为AB的中点,G为AO的中点,
∴AG=AO=1,
∵,则,
∴EG=,
∴点E的坐标为(-1,),
∵,,
∴,
∴,则,
∴NG=,则NO=1-,
∴点N的坐标为(,),
设直线QE的解析式为,
则,
解得:,
∴直线QE的解析式为,
把代入,得;
∴
③∵,
∴.
综上所述,符合条件的点为:、、.
8.解:(1)将,代入,求得,
∴;
(2)如图,D点关于PQ与A点对称,过点Q作于
∵,,
∴
∴四边形为菱形
∵
∴
∴
∴,
∴
∵
∴
∵D在二次函数上
∴
∴,或(舍去)
∴;
(3)存在满足条件的点E,点E的坐标为或或或
如上图,过点Q作于D,此时
∵,,,
∴,,
∴,
∵
∴
∴
∴,;
①如下图,作AQ的垂直平分线,交AQ于E
此时,即为等腰三角形
设,则,
∴在中,,解得
∴
∴;
②如下图,以Q为圆心,AQ长半径画圆,交x轴于E
此时
∵
∴
∴
∴;
③当时
1)当E在A点左边时
∵
∴
2)当E在A点右边时
∵
∴;
综上所述,存在满足条件的点E,点E的坐标为或或或.
9.解:(1)∵y=x2+mx+4m与x轴交于,0)和点B(,0),
∴是方程x2+mx+4m=0的两个根,
,
,
∴(-2m)2-16m=20,
解得m1=5,m2=-1,
∵对称轴在y轴的右侧,
∴m=-1,
∴y=-x-4;
(2)y=-x-4中,当x=0时,y=-4,
当y=0时=-2,=4,
∴A(-2,0),B(4,0),C(0,-4),
过点AC作直线交对称轴于点M,
设直线AC的解析式为y=kx+b,
将(-2,0),(0,-4)代入,
则,
解得,
得y=-2x-4,当x=1时,y=-6,
∴M(1,-6);
(3)直线BC的解析式为y=k1x+b1,
将(4,0),(0,-4)代入,
则,
解得,
得y=x-4,
∴∠OCB=∠OBC=45°,
设P的横坐标为x,作PH⊥y轴于H,
则PC=,
∴PQ=|(x-4)--x-4)|
(图一) (图二)
如图一图二,当CQ=CP时,(x-4)+-x-4)=-8,
x=0,不合题意,所以不存在;
(图三) (图四) (图五)
如图三,当PC=PQ时,=(x-4)- -x-4),
解得x=,
∴P()
如图四,当CQ=PQ时,x=(x-4)- -x-4),
解得x=2,
∴P(2,-2);
如图五,当PC=PQ时 ,
-x-4)-(x-4)=,
解得:x=,
∴P();
综上:P1() ,P2(2,-2),P3().
10.解:(1)∵二次函数的图象与x轴交于点B(-2,0)、C(8,0),与y轴交于A(0,-4)
∴ ,
解得: ,
∴二次函数表达式是;
(2)∵AB2=BO2+AO2=20,AC2=AO2+OC2=80.
∵BC2=(BO+OC)2=100,
∴AB2+AC2=BC2.
∴△ABC是直角三角形;
设点N的坐标为(n,0),
∵∠AOB=∠NMA=90°,
∴有两种情况:
①当时,
∵,
∴
∴
∴=8-n
Rt△OAN中,
即
解得:n=3
∴n(3,0)
②当时,
∵NM∥AB
∴
∴
即N与原点O重合,
∴此时N(0,0)
综合①②得,N点坐标是(3,0)或(0,0).
(3)由(2)知,AC=,
①以A为圆心,以AC长为半径作圆,交x轴于N,此时N的坐标为( 8,0),
②以C为圆心,以AC长为半径作圆,交x轴于N,此时N的坐标为(,0)或(8+4,0);
③如图,作AC的垂直平分线交AC于M,交x轴于N,
∴△AOC∽△NMC.
∴,即,
∴CN=5.
∴此时N的坐标为(3,0),
综上,若点N在x轴上运动,当以点A、N、C为顶点的三角形是等腰三角形时,点N的坐标分别为(-8,0)、(8-4,0)、(3,0)、(8+4,0).
11.解:(1)设抛物线的解析式为,
经过点、,
根据题意得,
解得
所以抛物线的解析式为.
(2)的形状是等腰三角形.
理由:根据题意得,,.
∵,,,
∴,即的形状是等腰三角形.
(3)存在,理由:
设,
根据题意,得.
∵
∴,解得,
∴,.
12.解:(1)∵点A的坐标为,AB⊥x轴于点B,
∴B(6,0),
∴AB=,
∵点A的坐标为,AC⊥y轴于点C,
∴C(0,),
∴AC=6,
∵AB⊥x轴,AC⊥y轴,
∴∠ABO=∠ACO=90°=∠BOC,
∴四边形OBAC是矩形,
∴∠BAC=90°,
在Rt△ABC中,tan∠ACB=,
∴∠ACB=60°;
(2)由(1)知,C(0,),
∵点D是AC的中点,
∴D(3,),
设抛物线的解析式为y=ax2+bx+c,
将点A(6,),D(3,),O(0,0)代入抛物线解析式中,得,
∴,
∴抛物线的解析式为,
令y=0,则,
∴x=0或x=9,
∴G(9,0);
(3)如图,
当点F从点E运动到点O时,点M的运动轨迹是线段MM',
∴以DM为边的等边三角形的顶点P的轨迹是线段PP',
当抛物线过原点时,DG与AB的交点记作点M,当抛物线过点E时,DG'与AB的交点为M',
∵△DMP是等边三角形,
∴DM=DP,∠MDP=60°,
∵△DM'P'是等边三角形
∴DM'=DP',∠M'DP'=60°,
∴∠MDM'=∠PDP',
∴△MDM'≌△PDP'(SAS),
∴PP'=MM',
由(2)知,G(9,0),
∵D(3,),
∴直线DG的解析式,
令x=6,则y=,
∴M,
当抛物线过点E时,即抛物线过点A,D,E,
设抛物线的解析式为,
∴,
∴,
∴过点A,D,E的抛物线的解析式为,
令y=0,则,
∴x=﹣3或x=12,
∴G'(12,0),
∴DG'的解析式为,
令x=6,则y=,
∴M'(6,),
∴PP'=MM'=,
即点P运动的路径的长为.
同课章节目录
