必修3 第一章 算法初步 1.1算法与程序框图同步训练B卷(含详细解析)
文档属性
| 名称 | 必修3 第一章 算法初步 1.1算法与程序框图同步训练B卷(含详细解析) |  | |
| 格式 | zip | ||
| 文件大小 | 754.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-09-10 14:09:33 | ||
图片预览


文档简介
必修3 第一章 算法初步 算法与程序框图同步训练B卷(含详细解析)
一.选择题(共17小题)
1.集合P={x|x=2k,k∈Z},若对任意的a,b∈P都有a*b∈P,则运算*不可能是( )
A. 加法 B.减法 C.乘法 D.除法
2.下列运算不属于我们所讨论算法范畴的是( )
A. 已知圆的半径求圆的面积
B. 随意抽4张扑克牌算到二十四点的可能性
C. 已知坐标平面内两点求直线方程
D. 加减乘除法运算法则
3.如图程序框图中虚线框表示算法三种基本逻辑结构中的那种结构( )
A. 顺序结构 B.条件结构 C. 循环结构 D. 当型结构
4.算法:第一步 x=a;第二步 若b>x则x=b;第三步 若c>x,则x=c; 第四步 若d>x,则x=d; 第五步 输出x.则输出的x表示( )
A. a,b,c,d中的最大值 B. a,b,c,d中的最小值
C. 将a,b,c,d由小到大排序 D. 将a,b,c,d由大到小排序
5.算法:
S1 m=a
S2 若b<m,则m=b
S3 若c<m,则m=c
S4 若d<m,则 m=d
S5 输出m,则输出m表示( )
A. a,b,c,d中最大值 B.a,b,c,d中最小值
C. 将a,b,c,d由小到大排序 D.将a,b,c,d由大到小排序
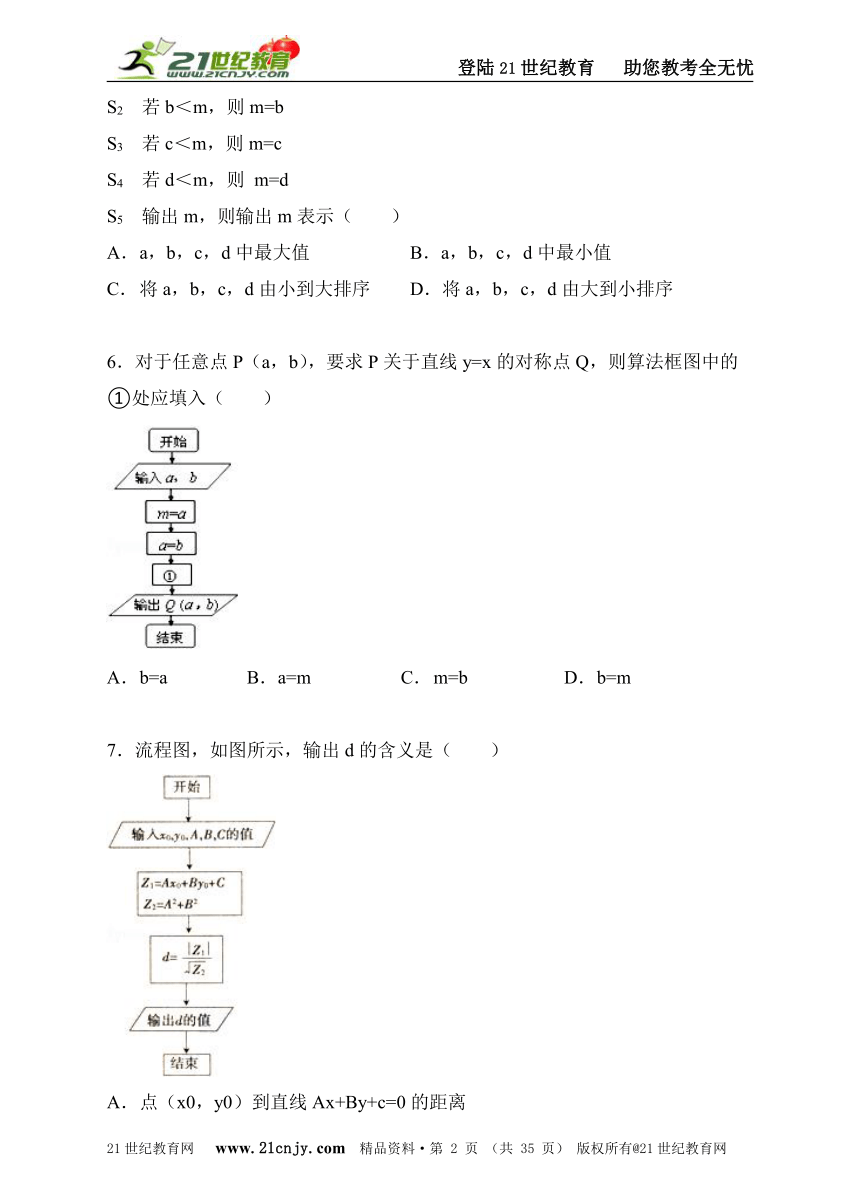
6.对于任意点P(a,b),要求P关于直线y=x的对称点Q,则算法框图中的①处应填入( )
A. b=a B.a=m C. m=b D. b=m
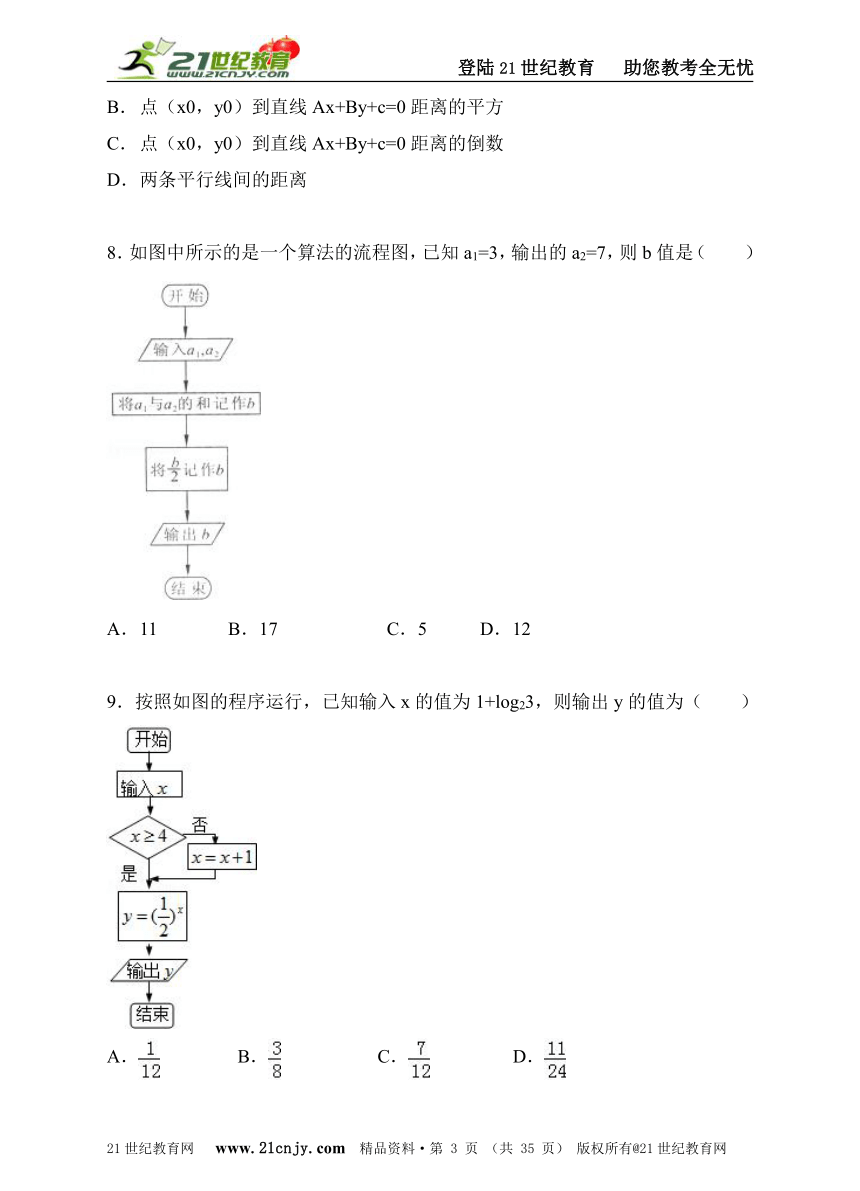
7.流程图,如图所示,输出d的含义是( )
A. 点(x0,y0)到直线Ax+By+c=0的距离
B. 点(x0,y0)到直线Ax+By+c=0距离的平方
C. 点(x0,y0)到直线Ax+By+c=0距离的倒数
D. 两条平行线间的距离
8.如图中所示的是一个算法的流程图,已知a1=3,输出的a2=7,则b值是( )
A. 11 B.17 C.5 D.12
9.按照如图的程序运行,已知输入x的值为1+log23,则输出y的值为( )
A. B. C. D.
10.阅读如图的程序框图.若输入n=6,则输出k的值为( )
A. 2 B. 3 C.4 D.5
11.一个算法的程序框图如图所示,该程序输出的结果为( )
A. B. C. D.
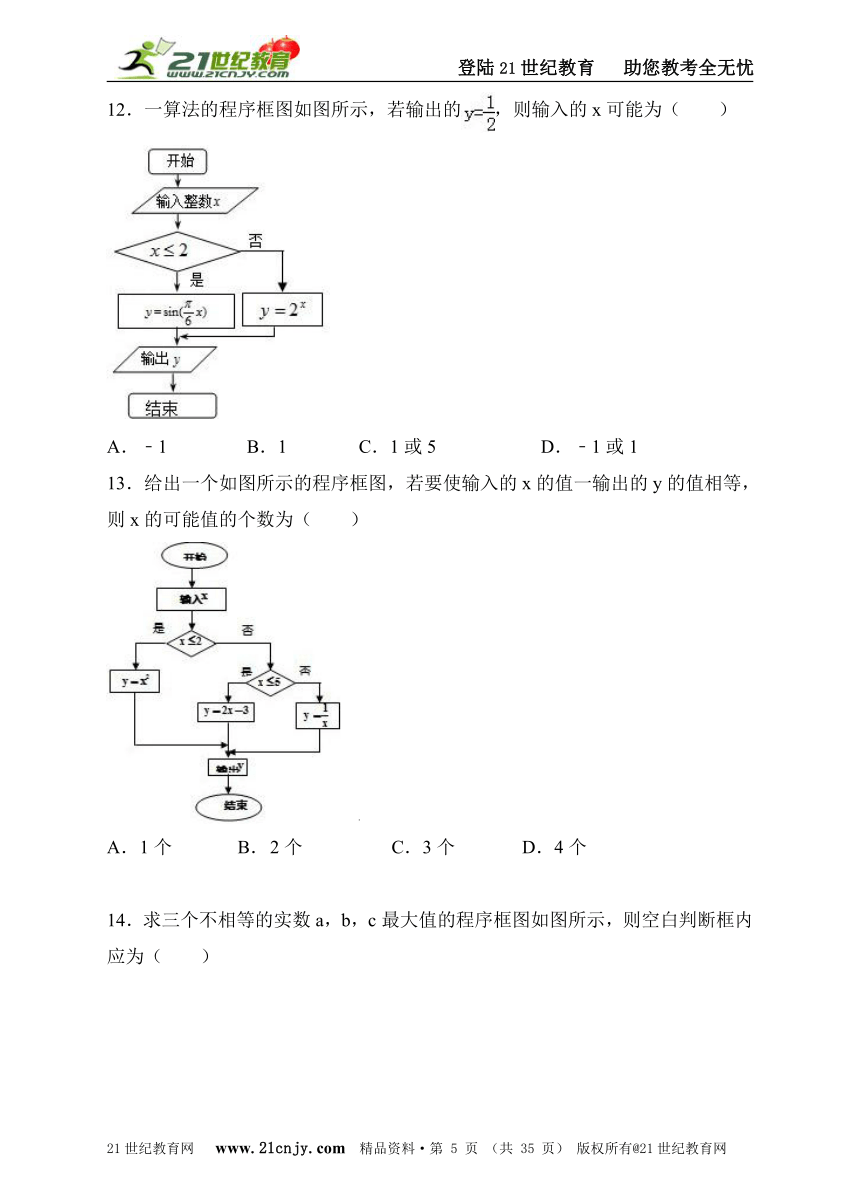
12.一算法的程序框图如图所示,若输出的,则输入的x可能为( )
A. ﹣1 B.1 C.1或5 D.﹣1或1
13.给出一个如图所示的程序框图,若要使输入的x的值一输出的y的值相等,则x的可能值的个数为( )2·1·c·n·j·y
A. 1个 B. 2个 C.3个 D.4个
14.求三个不相等的实数a,b,c最大值的程序框图如图所示,则空白判断框内应为( )
A. a>b? B. a>c? C. d>b 或 a>c? D. a>b 且 a>c?
15.如图,给出的是计算的值的一个程序框图,则图中判断框内(1)处和执行框中的(2)处应填的语句是( )21·世纪*教育网
A. i>100,n=n+1 B.i>100,n=n+2
C. i>50,n=n+2 D.i≤50,n=n+2
16.某程序框图如图所示,现输入如下四个函数,则可以输出的函数是( )
A. f(x)=x2 B.f(x)= C. f(x)=ex D.f(x)=sinx
17.运行如图所示的程序框图,输入下列四个函数,则可以输出的函数是( )
A. f(x)=x2 B.f(x)=cos2x C.f(x)=ex D. f(x)= sinπx
二.填空题(共9小题)
18.如图表示的算法结构是 _________ 结构.
19.运行下面的算法流程,若输出的y值的范围是[0,10],则输入的x值的范围是 _________ .21cnjy.com
20.如图的程序框图所示,若输入a=3,b=2,则输出的值是 _________ .
21.如图是求函数值的流程图,当输出y的值为1时,则输入的x的值为 _________ .
22.已知程序框图如图,则输出的i= _________ .
23.执行如图的程序框图,输出的S= _________ .
24.执行如图所示的程序框图,若输出x的值为23,则输入的x值为 _________ .
25.下面给出了解决问题的算法:
S1 输入x
S2 若x≤1则执行S3,否则执行S4
S3 使y=2x﹣3
S4 使y=x2﹣3x+3
S5 输出y
当输入的值为 _________ 时,输入值与输出值相等.
26.下面的语句是一个计算机程序的操作说明:
(1)初始值为x=1,y=1,z=0,n=0;
(2)n=n+1(将当前n+1的值赋予新的n);
(3)x=x+2(将当前x+2的值赋予新的x);
(4)y=2y(将当前2y的值赋予新的y);
(5)z=z+xy(将当前z+xy的值赋予新的z);
(6)如果z>7000,则执行语句(7),否则返回语句(2)继续进行;
(7)打印n,z;
(8)程序终止.
由语句(7)打印出的数值为 _________ , _________ .
三.解答题(共4小题)
27.在如图所示的程序框图中,记所有的x的值组成的集合为A,由输出的数据y组成的集合为B.
(1)分别写出集合A,B;
(2)在集合A中任取一个元素a,在集合B中任取一个元素b,求所得的两数中满足a>b的概率.
28.根据如图所示的程序框图,输入一个正整数n,将输出的x值依次记为x1,x2,x3,…,xn;输出的y值依次记为y1,y2,y3,…,yn.21·cn·jy·com
(1)求数列{xn}的通项公式;
(2)写出y1,y2,y3,y4的值,由此猜想出数列{yn}的通项公式;
(3)若zn=x1y1+x2y2+…+xnyn,求zn.
29.已知数列{an}的前n项和是Sn,且满足Sn=2an﹣1
(1)求数列{an}的通项公式;
(2)若数列{bn}满足an?bn=2n﹣1,求数列{bn}的前n项和Tn;
(3)请阅读如图所示的流程图,根据流程图判断该算法能否有确定的结果输出?并说明理由.
30.铁路部门托运行李的收费方法如下:y是收费额(单位:元),x是行李重量(单位:㎏),当0<x≤20时,按0.35/㎏收费,当x>20㎏时,20㎏的部分按0.35元/㎏,超出20㎏的部分,则按0.65元/㎏收费.21世纪教育网版权所有
(1)请根据上述收费方法求出y关于x的函数式;
(2)画出流程图.
(3)请你为该铁路部门设计一个计算行李托运费的程序.
参考答案及解析
一.选择题(共17小题)
1.集合P={x|x=2k,k∈Z},若对任意的a,b∈P都有a*b∈P,则运算*不可能是( )
A. 加法 B.减法 C.乘法 D.除法
答案:B
解:算法通常是指按照一定规则解决某一类问题的明确和有限步骤,且运用计算机执行后都能得到正确的结果.2-1-c-n-j-y
选项A、C、D都能写出明确和有限步骤,且执行后都能得到正确的结果;
选项B虽说能算出全部情况,但不能写出准确的步骤,所以不属于我们所讨论的算法范畴.
故选B.
3.如图程序框图中虚线框表示算法三种基本逻辑结构中的那种结构( )
A. 顺序结构 B.条件结构 C. 循环结构 D. 当型结构
答案:A
解:x=a,若b>x,则b>a,x=b,否则x=a,即x为a,b中较大的值;
若c>x,则x=c,否则x仍为a,b中较大的值,即x为a,b,c中较大的值;
若d>x,则x=d,否则x仍为a,b,c中较大的值,即x为a,b,c中较大的值.
故x为a,b,c,d中最大的数,
故选A.
5.算法:
S1 m=a
S2 若b<m,则m=b
S3 若c<m,则m=c
S4 若d<m,则 m=d
S5 输出m,则输出m表示( )
A. a,b,c,d中最大值 B.a,b,c,d中最小值
C. 将a,b,c,d由小到大排序 D.将a,b,c,d由大到小排序
答案:B
6.对于任意点P(a,b),要求P关于直线y=x的对称点Q,则算法框图中的①处应填入( )
A. b=a B.a=m C. m=b D. b=m
答案:D
解:因为(a,b)与(b,a)关于y=x对称,
所以通过赋值,a赋值到m,b赋值给a,那么m赋值给b,完成a,b的交换,
所以①处应该填写b=m,
故选D.
7.流程图,如图所示,输出d的含义是( )
A. 点(x0,y0)到直线Ax+By+c=0的距离
B. 点(x0,y0)到直线Ax+By+c=0距离的平方
C. 点(x0,y0)到直线Ax+By+c=0距离的倒数
D. 两条平行线间的距离
答案:A
解:根据流程图,可得
结合点到直线的距离公式,可知输出d的含义是点(x0,y0)到直线Ax+By+c=0的距离
故选A.
8.如图中所示的是一个算法的流程图,已知a1=3,输出的a2=7,则b值是( )
9.按照如图的程序运行,已知输入x的值为1+log23,则输出y的值为( )
A. B. C. D.
答案:A
解:根据框图的流程,输入x=1+log23<4,
则x=2+log23,∴输出y=×=×=.
故选:A.
10.阅读如图的程序框图.若输入n=6,则输出k的值为( )
A. 2 B. 3 C.4 D.5
答案:B
解:当n输入值为6时,用2×6+1=13替换n,13不大于100,用0+1=1替换k,再用2×13+1=27替换n,27不大于100,此时用1+1=2替换k,再用27×2+1=55替换n,此时55不大于100,用2+1=3替换k,再用2×55+1=111替换n,此时111大于100,算法结束,输出k的值为3.【来源:21·世纪·教育·网】
故选B.
11.一个算法的程序框图如图所示,该程序输出的结果为( )
A. B. C. D.
答案:B
解:i=1,满足条件i≤9,执行循环体,S=
i=2,满足条件i≤9,执行循环体,S=+
依此类推
i=9,满足条件i≤9,执行循环体,S=++…
i=10,不满足条件i≤9,退出循环体,输出S=1﹣=
故选B.
12.一算法的程序框图如图所示,若输出的,则输入的x可能为( )
A. ﹣1 B.1 C.1或5 D.﹣1或1
答案:B
解:这是一个用条件分支结构设计的算法,
该程序框图所表示的算法的作用是求分段函数y=的函数值,
输出的结果为,当x≤2时,sin=,解得x=1+12k,或x=5+12k,k∈Z,即x=1,﹣7,﹣11,… 21*cnjy*com
当x>2时,2x=,解得x=﹣1(不合,舍去),
则输入的x可能为1.
故选B.
13.给出一个如图所示的程序框图,若要使输入的x的值一输出的y的值相等,则x的可能值的个数为( )【来源:21cnj*y.co*m】
A. 1个 B. 2个 C.3个 D.4个
答案:C
解:分析程序中各变量、各语句的作用,
再根据流程图所示的顺序,可知:
该程序的作用是计算并输出分段函数y=的值
又∵输入的x值与输出的y值相等
当x≤2时,x=x2,解得x=0,或x=1
当2<x≤5时,x=2x﹣3,解得x=3,
当x>5时,x=,解得x=±1(舍去)
故满足条件的x值共有3个
故选C.
14.求三个不相等的实数a,b,c最大值的程序框图如图所示,则空白判断框内应为( )
A. a>b? B. a>c? C. d>b 或 a>c? D. a>b 且 a>c?
答案:D
解:由题意,程序求a,b,c中的最大值
第1步,比较a与b、c的大小,当a比b、c都大时,输出a的值;
当a不能比b、c都大时,进入第2步;
第2步,由于a不是最大值,所以比较b、c的大小
当b>c时,输出b;当b<c时,输出c
综上所述,空白判断框内应填上:a>b 且 a>c?
故选:D
15.如图,给出的是计算的值的一个程序框图,则图中判断框内(1)处和执行框中的(2)处应填的语句是( )www.21-cn-jy.com
A. i>100,n=n+1 B.i>100,n=n+2
C. i>50,n=n+2 D.i≤50,n=n+2
答案:C
解:此时,经第一次循环得到的结果是,经第二次循环得到的结果是
经第三次循环得到的结果是
据观察S中最后一项的分母与i的关系是分母=2(i﹣1)
令2(i﹣1)=100解得i=51即需要i=51时输出
故图中判断框内(1)处和执行框中的(2)处应填的语句是分别是i>50,n=n+2
故选C
16.某程序框图如图所示,现输入如下四个函数,则可以输出的函数是( )
A. f(x)=x2 B.f(x)= C. f(x)=ex D.f(x)=sinx
答案:D
解:∵A:f(x)=x2、C:f(x)=ex,不是奇函数,故不满足条件①
又∵B:f(x)=的函数图象与x轴没有交点,故不满足条件②
而D:f(x)=sinx既是奇函数,而且函数图象与x也有交点,
故D:f(x)=sinx符合输出的条件
故选D.
17.运行如图所示的程序框图,输入下列四个函数,则可以输出的函数是( )
A. f(x)=x2 B.f(x)=cos2x C.f(x)=ex D. f(x)= sinπx
答案:D
解:∵A:f(x)=x2、C:f(x)=ex,不是周期函数,故不满足条件f(x)=f(x+2),
又∵B:f(x)=cos2x的函数是周期函数,但其周期是π,故不满足条件②
而D:f(x)=sinπx存在零点,而且其周期是2,
故D:f(x)=sinπx符合要求.
故答案为D.
二.填空题(共9小题)
18.如图表示的算法结构是 顺序 结构.
解:算法结构有三种:
顺序结构,按从上到下的顺序进行;
选择结构,根据条件作判断,再决定执行哪一种操作的算法结构,必须包含判断框;
循环结构,从某处开始,按照一定条件,反复执行某一处理步骤.
如图所示的算法结构是顺序结构.
故答案为:顺序.
19.运行下面的算法流程,若输出的y值的范围是[0,10],则输入的x值的范围是 [﹣7,9] .
解:该程序的作用是计算分段函数y=,
当y=0,解得x=﹣7,
当y=10,解得x=9,
则输入的x值的范围是;[﹣7,9].
故答案为:[﹣7,9].
20.如图的程序框图所示,若输入a=3,b=2,则输出的值是 2 .
解:由已知中的流程图可得,该程序的功能是计算并输出分段函数y=的值,
∵a=3,b=2,满足a>b
故y===2
故答案为:2.
21.如图是求函数值的流程图,当输出y的值为1时,则输入的x的值为 1 .
解:当x<0时,y=2x﹣3,令2x﹣3=1,解得x=2,不满足条件;
当x≥0时,y=3﹣2x,令3﹣2x=1,解得x=1,满足条件;
故答案为:1
22.已知程序框图如图,则输出的i= 9 .
解:S=1,i=3不满足条件S≥100,执行循环体
S=1×3=3,i=3+2=5,不满足条件S≥100,执行循环体
S=3×5=15,i=5+2=7,不满足条件S≥100,执行循环体
S=15×7=105,i=7+2=9,满足条件S≥100,退出循环体
此时i=9
故答案为:9
23.执行如图的程序框图,输出的S= 3 .
解:由程序框图得:第一次运行S=1?log23,k=3;
第二次运行S=1?log23?log34,k=4;
第三次运行S=1?log23?log34?log45,k=5;
…
直到k=8时,程序运行终止,此时S=1?log23?log34…log78=?…=log28=3.www-2-1-cnjy-com
故答案为:3.
24.执行如图所示的程序框图,若输出x的值为23,则输入的x值为 2 .
解:模拟程序的执行情况如下:
x←2×x+1,n=1+1=2,满足n≤3,执行循环体;
x=2×(2x+1)+1,n=2+1=3,满足n≤3,执行循环体;
x=2×(4x+3)+1=23,n=3+1=4,不满足n≤3,退出循环体,
由2×(4x+3)+1=23即可得x=2.
则输入的x值为:2
故答案为:2.
25.下面给出了解决问题的算法:
S1 输入x
S2 若x≤1则执行S3,否则执行S4
S3 使y=2x﹣3
S4 使y=x2﹣3x+3
S5 输出y
当输入的值为 3 时,输入值与输出值相等.
解:分析程序中各变量、各语句的作用,
再根据流程图所示的顺序,可知:
该程序的作用是计算并输出分段函数 的函数值.
当输入的值为x时,输入值与输出值相等,
当x>1时,若x2﹣3x+3=x,则x=3或x=1(舍去),
当x≤1时,若2x﹣3=x,则x=3(舍去)
故答案为3.
26.下面的语句是一个计算机程序的操作说明:
(1)初始值为x=1,y=1,z=0,n=0;
(2)n=n+1(将当前n+1的值赋予新的n);
(3)x=x+2(将当前x+2的值赋予新的x);
(4)y=2y(将当前2y的值赋予新的y);
(5)z=z+xy(将当前z+xy的值赋予新的z);
(6)如果z>7000,则执行语句(7),否则返回语句(2)继续进行;
(7)打印n,z;
(8)程序终止.
由语句(7)打印出的数值为 n=8 , z=7682 .
解:由操作说明可以看出变量x的变化是首项为1,公差为2的数列,故其数值分别为3,5,7,9,…,2n+1,..【出处:21教育名师】
变量y是首项为1,公比为2的等比数列的项,故其数值分别为2,4,8,16,…,2n,…
z=z+xy
验证发现,当n=8时,z=7682,符合循环条件,
故答案为n=8,z=7682
三.解答题(共4小题)
27.在如图所示的程序框图中,记所有的x的值组成的集合为A,由输出的数据y组成的集合为B.
(1)分别写出集合A,B;
(2)在集合A中任取一个元素a,在集合B中任取一个元素b,求所得的两数中满足a>b的概率.
解:(1)由框图可知A={6,8,10,12,14},B={5,7,9,11,13}.(3分)
(2)其中基本事件的总数为5×5=25,
设两数中满足“a>b”为事件E,当a=6时,b=5;
当a=8时,b=5,7;当a=10时,b=5,7,9;
当a=12时,b=5,7,9,11;
当a=14时,b=5,7,9,11,13,事件E包含基本事件为15,
则.(10分)
28.根据如图所示的程序框图,输入一个正整数n,将输出的x值依次记为x1,x2,x3,…,xn;输出的y值依次记为y1,y2,y3,…,yn.【版权所有:21教育】
(1)求数列{xn}的通项公式;
(2)写出y1,y2,y3,y4的值,由此猜想出数列{yn}的通项公式;
(3)若zn=x1y1+x2y2+…+xnyn,求zn.
解:(1)由程序框图可知:{xn}是等差数列,且首项x1=1,公差d=2
∴xn=1+2(n﹣1)=2n﹣1…(3分)
(2)y1=2=3﹣1,y2=3×2+2=8=32﹣1,y3=3×8+2=26=33﹣1,y4=3×26+2=80=34﹣121教育名师原创作品
故yn=3n﹣1…(7分)
(3)xn?yn=(2n﹣1)(3n﹣1)=(2n﹣1)?3n﹣(2n﹣1),
∴zn=(3﹣1)+(3?32﹣3)+(5?33﹣5)+…+[(2n﹣1)?3n﹣(2n﹣1)]
=3+3?32+5?33+…+(2n﹣1)?3n﹣[1+3+5+(2n﹣1)]
=3+3?32+5?33+…+(2n﹣1)?3n﹣n2
令Sn=3+3?32+5?33+…+(2n﹣1)?3n3Sn=32+3?33+5?34+…+(2n﹣1)?3n+1
∴﹣2Sn=3+2(32+33+34+…+3n)﹣(2n﹣1)?3n+1=2(1﹣n)?3n+1﹣6
∴Sn=(n﹣1)?3n+1+3
∴zn=(n﹣1)?3n+1+3﹣n2…(14分)
29.已知数列{an}的前n项和是Sn,且满足Sn=2an﹣1
(1)求数列{an}的通项公式;
(2)若数列{bn}满足an?bn=2n﹣1,求数列{bn}的前n项和Tn;
(3)请阅读如图所示的流程图,根据流程图判断该算法能否有确定的结果输出?并说明理由.
解:(1)由Sn=2an﹣1得,sn﹣1=2an﹣1﹣1﹣﹣﹣﹣﹣﹣﹣﹣﹣1分
当n≥2时,an=sn﹣sn﹣1,an=(2an﹣1)﹣(2an﹣1﹣1)
∴
∴{an}是以2为公比的等比数列﹣﹣﹣﹣﹣﹣﹣4分
令n=1得a1=2a1﹣1,
∴a1=1,
∴{an}的通项公式是an=2n﹣1﹣﹣﹣﹣﹣﹣﹣﹣﹣5分
(2)由﹣﹣﹣﹣﹣﹣﹣﹣6分
∴﹣﹣﹣﹣﹣﹣﹣﹣7分
∴﹣8分
相减得:﹣﹣﹣9分
∴,﹣﹣﹣﹣﹣﹣﹣10分
(3)没有确定的结果输出!﹣﹣﹣﹣﹣﹣﹣11分
原因如下:该流程图的作用首先是求出数列{bn}的前n项和Tn,
然后找出数列{bn}中使Tn>6成立的第一项,并输出Tn,n的值,﹣﹣﹣﹣﹣﹣﹣12分
而由(2)可得数列{bn}的前n项和Tn<6,不可能满足Tn>6,﹣﹣﹣﹣﹣﹣﹣13分
所以该程序将永远执行下去没有确定的结果输出.
30.铁路部门托运行李的收费方法如下:y是收费额(单位:元),x是行李重量(单位:㎏),当0<x≤20时,按0.35/㎏收费,当x>20㎏时,20㎏的部分按0.35元/㎏,超出20㎏的部分,则按0.65元/㎏收费.21教育网
(1)请根据上述收费方法求出y关于x的函数式;
(2)画出流程图.
(3)请你为该铁路部门设计一个计算行李托运费的程序.
解:出y关于x的函数式为:
…3分
(2)框图如下…6分
(3)程序如图8分
一.选择题(共17小题)
1.集合P={x|x=2k,k∈Z},若对任意的a,b∈P都有a*b∈P,则运算*不可能是( )
A. 加法 B.减法 C.乘法 D.除法
2.下列运算不属于我们所讨论算法范畴的是( )
A. 已知圆的半径求圆的面积
B. 随意抽4张扑克牌算到二十四点的可能性
C. 已知坐标平面内两点求直线方程
D. 加减乘除法运算法则
3.如图程序框图中虚线框表示算法三种基本逻辑结构中的那种结构( )
A. 顺序结构 B.条件结构 C. 循环结构 D. 当型结构
4.算法:第一步 x=a;第二步 若b>x则x=b;第三步 若c>x,则x=c; 第四步 若d>x,则x=d; 第五步 输出x.则输出的x表示( )
A. a,b,c,d中的最大值 B. a,b,c,d中的最小值
C. 将a,b,c,d由小到大排序 D. 将a,b,c,d由大到小排序
5.算法:
S1 m=a
S2 若b<m,则m=b
S3 若c<m,则m=c
S4 若d<m,则 m=d
S5 输出m,则输出m表示( )
A. a,b,c,d中最大值 B.a,b,c,d中最小值
C. 将a,b,c,d由小到大排序 D.将a,b,c,d由大到小排序
6.对于任意点P(a,b),要求P关于直线y=x的对称点Q,则算法框图中的①处应填入( )
A. b=a B.a=m C. m=b D. b=m
7.流程图,如图所示,输出d的含义是( )
A. 点(x0,y0)到直线Ax+By+c=0的距离
B. 点(x0,y0)到直线Ax+By+c=0距离的平方
C. 点(x0,y0)到直线Ax+By+c=0距离的倒数
D. 两条平行线间的距离
8.如图中所示的是一个算法的流程图,已知a1=3,输出的a2=7,则b值是( )
A. 11 B.17 C.5 D.12
9.按照如图的程序运行,已知输入x的值为1+log23,则输出y的值为( )
A. B. C. D.
10.阅读如图的程序框图.若输入n=6,则输出k的值为( )
A. 2 B. 3 C.4 D.5
11.一个算法的程序框图如图所示,该程序输出的结果为( )
A. B. C. D.
12.一算法的程序框图如图所示,若输出的,则输入的x可能为( )
A. ﹣1 B.1 C.1或5 D.﹣1或1
13.给出一个如图所示的程序框图,若要使输入的x的值一输出的y的值相等,则x的可能值的个数为( )2·1·c·n·j·y
A. 1个 B. 2个 C.3个 D.4个
14.求三个不相等的实数a,b,c最大值的程序框图如图所示,则空白判断框内应为( )
A. a>b? B. a>c? C. d>b 或 a>c? D. a>b 且 a>c?
15.如图,给出的是计算的值的一个程序框图,则图中判断框内(1)处和执行框中的(2)处应填的语句是( )21·世纪*教育网
A. i>100,n=n+1 B.i>100,n=n+2
C. i>50,n=n+2 D.i≤50,n=n+2
16.某程序框图如图所示,现输入如下四个函数,则可以输出的函数是( )
A. f(x)=x2 B.f(x)= C. f(x)=ex D.f(x)=sinx
17.运行如图所示的程序框图,输入下列四个函数,则可以输出的函数是( )
A. f(x)=x2 B.f(x)=cos2x C.f(x)=ex D. f(x)= sinπx
二.填空题(共9小题)
18.如图表示的算法结构是 _________ 结构.
19.运行下面的算法流程,若输出的y值的范围是[0,10],则输入的x值的范围是 _________ .21cnjy.com
20.如图的程序框图所示,若输入a=3,b=2,则输出的值是 _________ .
21.如图是求函数值的流程图,当输出y的值为1时,则输入的x的值为 _________ .
22.已知程序框图如图,则输出的i= _________ .
23.执行如图的程序框图,输出的S= _________ .
24.执行如图所示的程序框图,若输出x的值为23,则输入的x值为 _________ .
25.下面给出了解决问题的算法:
S1 输入x
S2 若x≤1则执行S3,否则执行S4
S3 使y=2x﹣3
S4 使y=x2﹣3x+3
S5 输出y
当输入的值为 _________ 时,输入值与输出值相等.
26.下面的语句是一个计算机程序的操作说明:
(1)初始值为x=1,y=1,z=0,n=0;
(2)n=n+1(将当前n+1的值赋予新的n);
(3)x=x+2(将当前x+2的值赋予新的x);
(4)y=2y(将当前2y的值赋予新的y);
(5)z=z+xy(将当前z+xy的值赋予新的z);
(6)如果z>7000,则执行语句(7),否则返回语句(2)继续进行;
(7)打印n,z;
(8)程序终止.
由语句(7)打印出的数值为 _________ , _________ .
三.解答题(共4小题)
27.在如图所示的程序框图中,记所有的x的值组成的集合为A,由输出的数据y组成的集合为B.
(1)分别写出集合A,B;
(2)在集合A中任取一个元素a,在集合B中任取一个元素b,求所得的两数中满足a>b的概率.
28.根据如图所示的程序框图,输入一个正整数n,将输出的x值依次记为x1,x2,x3,…,xn;输出的y值依次记为y1,y2,y3,…,yn.21·cn·jy·com
(1)求数列{xn}的通项公式;
(2)写出y1,y2,y3,y4的值,由此猜想出数列{yn}的通项公式;
(3)若zn=x1y1+x2y2+…+xnyn,求zn.
29.已知数列{an}的前n项和是Sn,且满足Sn=2an﹣1
(1)求数列{an}的通项公式;
(2)若数列{bn}满足an?bn=2n﹣1,求数列{bn}的前n项和Tn;
(3)请阅读如图所示的流程图,根据流程图判断该算法能否有确定的结果输出?并说明理由.
30.铁路部门托运行李的收费方法如下:y是收费额(单位:元),x是行李重量(单位:㎏),当0<x≤20时,按0.35/㎏收费,当x>20㎏时,20㎏的部分按0.35元/㎏,超出20㎏的部分,则按0.65元/㎏收费.21世纪教育网版权所有
(1)请根据上述收费方法求出y关于x的函数式;
(2)画出流程图.
(3)请你为该铁路部门设计一个计算行李托运费的程序.
参考答案及解析
一.选择题(共17小题)
1.集合P={x|x=2k,k∈Z},若对任意的a,b∈P都有a*b∈P,则运算*不可能是( )
A. 加法 B.减法 C.乘法 D.除法
答案:B
解:算法通常是指按照一定规则解决某一类问题的明确和有限步骤,且运用计算机执行后都能得到正确的结果.2-1-c-n-j-y
选项A、C、D都能写出明确和有限步骤,且执行后都能得到正确的结果;
选项B虽说能算出全部情况,但不能写出准确的步骤,所以不属于我们所讨论的算法范畴.
故选B.
3.如图程序框图中虚线框表示算法三种基本逻辑结构中的那种结构( )
A. 顺序结构 B.条件结构 C. 循环结构 D. 当型结构
答案:A
解:x=a,若b>x,则b>a,x=b,否则x=a,即x为a,b中较大的值;
若c>x,则x=c,否则x仍为a,b中较大的值,即x为a,b,c中较大的值;
若d>x,则x=d,否则x仍为a,b,c中较大的值,即x为a,b,c中较大的值.
故x为a,b,c,d中最大的数,
故选A.
5.算法:
S1 m=a
S2 若b<m,则m=b
S3 若c<m,则m=c
S4 若d<m,则 m=d
S5 输出m,则输出m表示( )
A. a,b,c,d中最大值 B.a,b,c,d中最小值
C. 将a,b,c,d由小到大排序 D.将a,b,c,d由大到小排序
答案:B
6.对于任意点P(a,b),要求P关于直线y=x的对称点Q,则算法框图中的①处应填入( )
A. b=a B.a=m C. m=b D. b=m
答案:D
解:因为(a,b)与(b,a)关于y=x对称,
所以通过赋值,a赋值到m,b赋值给a,那么m赋值给b,完成a,b的交换,
所以①处应该填写b=m,
故选D.
7.流程图,如图所示,输出d的含义是( )
A. 点(x0,y0)到直线Ax+By+c=0的距离
B. 点(x0,y0)到直线Ax+By+c=0距离的平方
C. 点(x0,y0)到直线Ax+By+c=0距离的倒数
D. 两条平行线间的距离
答案:A
解:根据流程图,可得
结合点到直线的距离公式,可知输出d的含义是点(x0,y0)到直线Ax+By+c=0的距离
故选A.
8.如图中所示的是一个算法的流程图,已知a1=3,输出的a2=7,则b值是( )
9.按照如图的程序运行,已知输入x的值为1+log23,则输出y的值为( )
A. B. C. D.
答案:A
解:根据框图的流程,输入x=1+log23<4,
则x=2+log23,∴输出y=×=×=.
故选:A.
10.阅读如图的程序框图.若输入n=6,则输出k的值为( )
A. 2 B. 3 C.4 D.5
答案:B
解:当n输入值为6时,用2×6+1=13替换n,13不大于100,用0+1=1替换k,再用2×13+1=27替换n,27不大于100,此时用1+1=2替换k,再用27×2+1=55替换n,此时55不大于100,用2+1=3替换k,再用2×55+1=111替换n,此时111大于100,算法结束,输出k的值为3.【来源:21·世纪·教育·网】
故选B.
11.一个算法的程序框图如图所示,该程序输出的结果为( )
A. B. C. D.
答案:B
解:i=1,满足条件i≤9,执行循环体,S=
i=2,满足条件i≤9,执行循环体,S=+
依此类推
i=9,满足条件i≤9,执行循环体,S=++…
i=10,不满足条件i≤9,退出循环体,输出S=1﹣=
故选B.
12.一算法的程序框图如图所示,若输出的,则输入的x可能为( )
A. ﹣1 B.1 C.1或5 D.﹣1或1
答案:B
解:这是一个用条件分支结构设计的算法,
该程序框图所表示的算法的作用是求分段函数y=的函数值,
输出的结果为,当x≤2时,sin=,解得x=1+12k,或x=5+12k,k∈Z,即x=1,﹣7,﹣11,… 21*cnjy*com
当x>2时,2x=,解得x=﹣1(不合,舍去),
则输入的x可能为1.
故选B.
13.给出一个如图所示的程序框图,若要使输入的x的值一输出的y的值相等,则x的可能值的个数为( )【来源:21cnj*y.co*m】
A. 1个 B. 2个 C.3个 D.4个
答案:C
解:分析程序中各变量、各语句的作用,
再根据流程图所示的顺序,可知:
该程序的作用是计算并输出分段函数y=的值
又∵输入的x值与输出的y值相等
当x≤2时,x=x2,解得x=0,或x=1
当2<x≤5时,x=2x﹣3,解得x=3,
当x>5时,x=,解得x=±1(舍去)
故满足条件的x值共有3个
故选C.
14.求三个不相等的实数a,b,c最大值的程序框图如图所示,则空白判断框内应为( )
A. a>b? B. a>c? C. d>b 或 a>c? D. a>b 且 a>c?
答案:D
解:由题意,程序求a,b,c中的最大值
第1步,比较a与b、c的大小,当a比b、c都大时,输出a的值;
当a不能比b、c都大时,进入第2步;
第2步,由于a不是最大值,所以比较b、c的大小
当b>c时,输出b;当b<c时,输出c
综上所述,空白判断框内应填上:a>b 且 a>c?
故选:D
15.如图,给出的是计算的值的一个程序框图,则图中判断框内(1)处和执行框中的(2)处应填的语句是( )www.21-cn-jy.com
A. i>100,n=n+1 B.i>100,n=n+2
C. i>50,n=n+2 D.i≤50,n=n+2
答案:C
解:此时,经第一次循环得到的结果是,经第二次循环得到的结果是
经第三次循环得到的结果是
据观察S中最后一项的分母与i的关系是分母=2(i﹣1)
令2(i﹣1)=100解得i=51即需要i=51时输出
故图中判断框内(1)处和执行框中的(2)处应填的语句是分别是i>50,n=n+2
故选C
16.某程序框图如图所示,现输入如下四个函数,则可以输出的函数是( )
A. f(x)=x2 B.f(x)= C. f(x)=ex D.f(x)=sinx
答案:D
解:∵A:f(x)=x2、C:f(x)=ex,不是奇函数,故不满足条件①
又∵B:f(x)=的函数图象与x轴没有交点,故不满足条件②
而D:f(x)=sinx既是奇函数,而且函数图象与x也有交点,
故D:f(x)=sinx符合输出的条件
故选D.
17.运行如图所示的程序框图,输入下列四个函数,则可以输出的函数是( )
A. f(x)=x2 B.f(x)=cos2x C.f(x)=ex D. f(x)= sinπx
答案:D
解:∵A:f(x)=x2、C:f(x)=ex,不是周期函数,故不满足条件f(x)=f(x+2),
又∵B:f(x)=cos2x的函数是周期函数,但其周期是π,故不满足条件②
而D:f(x)=sinπx存在零点,而且其周期是2,
故D:f(x)=sinπx符合要求.
故答案为D.
二.填空题(共9小题)
18.如图表示的算法结构是 顺序 结构.
解:算法结构有三种:
顺序结构,按从上到下的顺序进行;
选择结构,根据条件作判断,再决定执行哪一种操作的算法结构,必须包含判断框;
循环结构,从某处开始,按照一定条件,反复执行某一处理步骤.
如图所示的算法结构是顺序结构.
故答案为:顺序.
19.运行下面的算法流程,若输出的y值的范围是[0,10],则输入的x值的范围是 [﹣7,9] .
解:该程序的作用是计算分段函数y=,
当y=0,解得x=﹣7,
当y=10,解得x=9,
则输入的x值的范围是;[﹣7,9].
故答案为:[﹣7,9].
20.如图的程序框图所示,若输入a=3,b=2,则输出的值是 2 .
解:由已知中的流程图可得,该程序的功能是计算并输出分段函数y=的值,
∵a=3,b=2,满足a>b
故y===2
故答案为:2.
21.如图是求函数值的流程图,当输出y的值为1时,则输入的x的值为 1 .
解:当x<0时,y=2x﹣3,令2x﹣3=1,解得x=2,不满足条件;
当x≥0时,y=3﹣2x,令3﹣2x=1,解得x=1,满足条件;
故答案为:1
22.已知程序框图如图,则输出的i= 9 .
解:S=1,i=3不满足条件S≥100,执行循环体
S=1×3=3,i=3+2=5,不满足条件S≥100,执行循环体
S=3×5=15,i=5+2=7,不满足条件S≥100,执行循环体
S=15×7=105,i=7+2=9,满足条件S≥100,退出循环体
此时i=9
故答案为:9
23.执行如图的程序框图,输出的S= 3 .
解:由程序框图得:第一次运行S=1?log23,k=3;
第二次运行S=1?log23?log34,k=4;
第三次运行S=1?log23?log34?log45,k=5;
…
直到k=8时,程序运行终止,此时S=1?log23?log34…log78=?…=log28=3.www-2-1-cnjy-com
故答案为:3.
24.执行如图所示的程序框图,若输出x的值为23,则输入的x值为 2 .
解:模拟程序的执行情况如下:
x←2×x+1,n=1+1=2,满足n≤3,执行循环体;
x=2×(2x+1)+1,n=2+1=3,满足n≤3,执行循环体;
x=2×(4x+3)+1=23,n=3+1=4,不满足n≤3,退出循环体,
由2×(4x+3)+1=23即可得x=2.
则输入的x值为:2
故答案为:2.
25.下面给出了解决问题的算法:
S1 输入x
S2 若x≤1则执行S3,否则执行S4
S3 使y=2x﹣3
S4 使y=x2﹣3x+3
S5 输出y
当输入的值为 3 时,输入值与输出值相等.
解:分析程序中各变量、各语句的作用,
再根据流程图所示的顺序,可知:
该程序的作用是计算并输出分段函数 的函数值.
当输入的值为x时,输入值与输出值相等,
当x>1时,若x2﹣3x+3=x,则x=3或x=1(舍去),
当x≤1时,若2x﹣3=x,则x=3(舍去)
故答案为3.
26.下面的语句是一个计算机程序的操作说明:
(1)初始值为x=1,y=1,z=0,n=0;
(2)n=n+1(将当前n+1的值赋予新的n);
(3)x=x+2(将当前x+2的值赋予新的x);
(4)y=2y(将当前2y的值赋予新的y);
(5)z=z+xy(将当前z+xy的值赋予新的z);
(6)如果z>7000,则执行语句(7),否则返回语句(2)继续进行;
(7)打印n,z;
(8)程序终止.
由语句(7)打印出的数值为 n=8 , z=7682 .
解:由操作说明可以看出变量x的变化是首项为1,公差为2的数列,故其数值分别为3,5,7,9,…,2n+1,..【出处:21教育名师】
变量y是首项为1,公比为2的等比数列的项,故其数值分别为2,4,8,16,…,2n,…
z=z+xy
验证发现,当n=8时,z=7682,符合循环条件,
故答案为n=8,z=7682
三.解答题(共4小题)
27.在如图所示的程序框图中,记所有的x的值组成的集合为A,由输出的数据y组成的集合为B.
(1)分别写出集合A,B;
(2)在集合A中任取一个元素a,在集合B中任取一个元素b,求所得的两数中满足a>b的概率.
解:(1)由框图可知A={6,8,10,12,14},B={5,7,9,11,13}.(3分)
(2)其中基本事件的总数为5×5=25,
设两数中满足“a>b”为事件E,当a=6时,b=5;
当a=8时,b=5,7;当a=10时,b=5,7,9;
当a=12时,b=5,7,9,11;
当a=14时,b=5,7,9,11,13,事件E包含基本事件为15,
则.(10分)
28.根据如图所示的程序框图,输入一个正整数n,将输出的x值依次记为x1,x2,x3,…,xn;输出的y值依次记为y1,y2,y3,…,yn.【版权所有:21教育】
(1)求数列{xn}的通项公式;
(2)写出y1,y2,y3,y4的值,由此猜想出数列{yn}的通项公式;
(3)若zn=x1y1+x2y2+…+xnyn,求zn.
解:(1)由程序框图可知:{xn}是等差数列,且首项x1=1,公差d=2
∴xn=1+2(n﹣1)=2n﹣1…(3分)
(2)y1=2=3﹣1,y2=3×2+2=8=32﹣1,y3=3×8+2=26=33﹣1,y4=3×26+2=80=34﹣121教育名师原创作品
故yn=3n﹣1…(7分)
(3)xn?yn=(2n﹣1)(3n﹣1)=(2n﹣1)?3n﹣(2n﹣1),
∴zn=(3﹣1)+(3?32﹣3)+(5?33﹣5)+…+[(2n﹣1)?3n﹣(2n﹣1)]
=3+3?32+5?33+…+(2n﹣1)?3n﹣[1+3+5+(2n﹣1)]
=3+3?32+5?33+…+(2n﹣1)?3n﹣n2
令Sn=3+3?32+5?33+…+(2n﹣1)?3n3Sn=32+3?33+5?34+…+(2n﹣1)?3n+1
∴﹣2Sn=3+2(32+33+34+…+3n)﹣(2n﹣1)?3n+1=2(1﹣n)?3n+1﹣6
∴Sn=(n﹣1)?3n+1+3
∴zn=(n﹣1)?3n+1+3﹣n2…(14分)
29.已知数列{an}的前n项和是Sn,且满足Sn=2an﹣1
(1)求数列{an}的通项公式;
(2)若数列{bn}满足an?bn=2n﹣1,求数列{bn}的前n项和Tn;
(3)请阅读如图所示的流程图,根据流程图判断该算法能否有确定的结果输出?并说明理由.
解:(1)由Sn=2an﹣1得,sn﹣1=2an﹣1﹣1﹣﹣﹣﹣﹣﹣﹣﹣﹣1分
当n≥2时,an=sn﹣sn﹣1,an=(2an﹣1)﹣(2an﹣1﹣1)
∴
∴{an}是以2为公比的等比数列﹣﹣﹣﹣﹣﹣﹣4分
令n=1得a1=2a1﹣1,
∴a1=1,
∴{an}的通项公式是an=2n﹣1﹣﹣﹣﹣﹣﹣﹣﹣﹣5分
(2)由﹣﹣﹣﹣﹣﹣﹣﹣6分
∴﹣﹣﹣﹣﹣﹣﹣﹣7分
∴﹣8分
相减得:﹣﹣﹣9分
∴,﹣﹣﹣﹣﹣﹣﹣10分
(3)没有确定的结果输出!﹣﹣﹣﹣﹣﹣﹣11分
原因如下:该流程图的作用首先是求出数列{bn}的前n项和Tn,
然后找出数列{bn}中使Tn>6成立的第一项,并输出Tn,n的值,﹣﹣﹣﹣﹣﹣﹣12分
而由(2)可得数列{bn}的前n项和Tn<6,不可能满足Tn>6,﹣﹣﹣﹣﹣﹣﹣13分
所以该程序将永远执行下去没有确定的结果输出.
30.铁路部门托运行李的收费方法如下:y是收费额(单位:元),x是行李重量(单位:㎏),当0<x≤20时,按0.35/㎏收费,当x>20㎏时,20㎏的部分按0.35元/㎏,超出20㎏的部分,则按0.65元/㎏收费.21教育网
(1)请根据上述收费方法求出y关于x的函数式;
(2)画出流程图.
(3)请你为该铁路部门设计一个计算行李托运费的程序.
解:出y关于x的函数式为:
…3分
(2)框图如下…6分
(3)程序如图8分
