小学数学北师大版五年级上倍数与因数整理与复习优秀教学课件(共19张ppt)
文档属性
| 名称 | 小学数学北师大版五年级上倍数与因数整理与复习优秀教学课件(共19张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 497.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-06 14:17:55 | ||
图片预览






文档简介
(共19张PPT)
第三单元 倍数与因数
整理与复习
本单元我们学习了哪些倍数与因数的问题?
2、5的倍数的特征
3的倍数的特征
认识倍数与因数
找因数
找质数
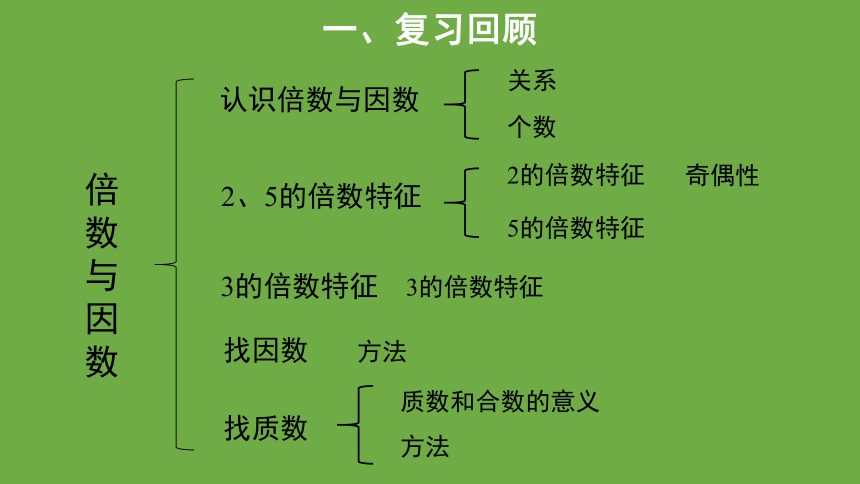
一、复习回顾
倍数与因数
认识倍数与因数
2、5的倍数特征
3的倍数特征
找因数
找质数
关系
个数
2的倍数特征
5的倍数特征
3的倍数特征
方法
质数和合数的意义
方法
奇偶性
一、复习回顾
倍数与因数
认识倍数与因数:认识自然数和整数,联系乘法认识倍数与因数。
倍数与因数是相互依存的关系,要说清谁是谁的倍数,谁是谁的因数。
一个数的倍数的个数是无限的。一个数的因数的个数是有限的。
一个数最小的因数是1,最大的因数是它本身;一个数最小的倍数是它本身,没有最大的倍数。
一、复习回顾
2、5的倍数特征
2的倍数的特征:个位上是0,2,4,6,8的数是2的倍数。
5的倍数的特征:个位上是0或5的数是5的倍数。
偶数和奇数的定义:是2的倍数的数叫偶数,不是2的倍数的数叫奇数。
既是2的倍数,又是5的倍数的特征:个位上是0的数既是2的倍数,又是5 的倍数。
3的倍数的特征:
3的倍数的特征:一个数各个数位上的数字的和是3的倍数,这个数就是3的倍数。
同时是2和3的倍数的特征:个位上的数是0,2,4,6,8,并且各个数位上的数字的和是3的倍数的数,既是2的倍数,又是3的倍数。
同时是3和5的倍数的特征:个位上的数是0或5,并且各个数位上的数字的和是3的倍数的数,既是3的倍数,又是5的倍数。
同时是2,3和5的倍数的特征:个位上的数是0,并且各个数位上的数字的和是3的倍数的数,既是2和5的倍数,又是3的倍数。
找因数
方法:运用乘法算式。思考:哪两个数相乘等于这个自然数。
一、复习回顾
找质数
质数与合数的意义:一个数只有1和它本身两个因数,这个数叫作质数。
一个数除了1和它本身以外还有别的因数,这个数叫作合数。
判断一个数是质数还是合数的方法:
首先可以用“2,5,3的倍数的特征”判断这个数是否有因数其次只要找到一个1和它本身以外的因数,就能肯定这个数是合数。如果除了1和它本身找不到其他因数,这个数就是质数。
一、复习回顾
二、基础练习
最小的质数是( ),最小的合数是( )。
2、5、8
4
( )既不是质数也不是合数。
1
2
要使四位数4□27是3 的倍数,方框里应填( )。
1.填空。
二、基础练习
自然数按是否是2 的倍数可分为( )和( )。
9和15
偶数
( )是所有非零自然数的因数。
1
奇数
20以内既是奇数又是合数的有( )。
1.填空。
二、基础练习
2.判断。
10÷2.5=4,所以10是2.5和4的倍数,2.5和4是10的因数。( )
如果a是b的最小倍数,则a=b。 ( )
奇数+偶数=奇数,奇数×偶数=奇数。 ( )
×
×
一个数的倍数一定大于它的因数。 ( )
一个合数至少有3个因数。 ( )
个位上是3、6、9的数是3的倍数。 ( )
×
√
×
√
我是一个偶数,也是一个两位数,十位数字与个位数字的积是18,我是多少呢?
1.猜数游戏。
答:36或92
三、强化练习
2. 分一分,填一填,并与同伴交流你的想法。
1 10 12 25 37 54 102 417 23 298
1
10
12
25
37
54
102
417
23
298
10
12
25
37
54
102
417
23
298
三、强化练习
3. 还有其他的包装方式吗?
6,5,3都是90的因数,所以每盒6瓶、5瓶、3瓶都正好装完。90的因数还有1,2,9,10,15,18,30,45,90。所以其他包装方式有每盒1瓶,2瓶,9瓶,10瓶,15瓶,18瓶,30瓶,45瓶,90瓶。
三、强化练习
4.选择题。
A质数 B合数 C奇数 D偶数
(1)两个质数的积一定是( )。
(2)两个合数的积一定是( )。
(3)当a是自然数时,2a+1一定是( )。
B
B
C
三、强化练习
A B C D E F G
A: 2的倍数;
B:最小的质数;
C: 既是奇数,又是合数;
D: 既不是质数,也不是合数
E: 最小的合数;
F: 既是2 的倍数,又是 3 的倍数;
G: 最大的因数是 5 。
8
2
9
1
4
6
5
A:2、4、6、8
B:2
C: 9
D: 1
E: 4
F: 6
G: 5
5.A、B、C、D、E、F、G分别代表不同的数字。
三、强化练习
哥德巴赫猜想(偶数情形):任何不小于4的偶数都可以写成两个质数相加的形式。
例如:4=2+2,6=3+3,8=3+5,…
哥德巴赫猜想
哥德巴赫猜想(奇数情形):任何不小于7的奇数都可以写成三个质数的和。
例如:7=2+2+3,9=2+2+5,…
对于哥德巴赫猜想的奇数情形,目前已经证明。
对于哥德巴赫猜想的偶数情形,目前最好的结果是我国数学家陈景润证明的结果:任何充分大的偶数都可以写成一个质数加上不超过两个质数的乘积的形式,通常称“1+2”。例如:50=17+3×11,16=2+2×7,…
四、拓展练习
10=( )+( )
11=( )+( )+( )
16=( )+( )
15=( )+( )+( )
40=( )+( )
21=( )+( )+( )
阅读了以上材料,请你在下面的括号里填上合适的质数。
四、拓展练习
3
7
3
13
3
37
5
5
11
3
5
7
2
2
7
再见
第三单元 倍数与因数
整理与复习
本单元我们学习了哪些倍数与因数的问题?
2、5的倍数的特征
3的倍数的特征
认识倍数与因数
找因数
找质数
一、复习回顾
倍数与因数
认识倍数与因数
2、5的倍数特征
3的倍数特征
找因数
找质数
关系
个数
2的倍数特征
5的倍数特征
3的倍数特征
方法
质数和合数的意义
方法
奇偶性
一、复习回顾
倍数与因数
认识倍数与因数:认识自然数和整数,联系乘法认识倍数与因数。
倍数与因数是相互依存的关系,要说清谁是谁的倍数,谁是谁的因数。
一个数的倍数的个数是无限的。一个数的因数的个数是有限的。
一个数最小的因数是1,最大的因数是它本身;一个数最小的倍数是它本身,没有最大的倍数。
一、复习回顾
2、5的倍数特征
2的倍数的特征:个位上是0,2,4,6,8的数是2的倍数。
5的倍数的特征:个位上是0或5的数是5的倍数。
偶数和奇数的定义:是2的倍数的数叫偶数,不是2的倍数的数叫奇数。
既是2的倍数,又是5的倍数的特征:个位上是0的数既是2的倍数,又是5 的倍数。
3的倍数的特征:
3的倍数的特征:一个数各个数位上的数字的和是3的倍数,这个数就是3的倍数。
同时是2和3的倍数的特征:个位上的数是0,2,4,6,8,并且各个数位上的数字的和是3的倍数的数,既是2的倍数,又是3的倍数。
同时是3和5的倍数的特征:个位上的数是0或5,并且各个数位上的数字的和是3的倍数的数,既是3的倍数,又是5的倍数。
同时是2,3和5的倍数的特征:个位上的数是0,并且各个数位上的数字的和是3的倍数的数,既是2和5的倍数,又是3的倍数。
找因数
方法:运用乘法算式。思考:哪两个数相乘等于这个自然数。
一、复习回顾
找质数
质数与合数的意义:一个数只有1和它本身两个因数,这个数叫作质数。
一个数除了1和它本身以外还有别的因数,这个数叫作合数。
判断一个数是质数还是合数的方法:
首先可以用“2,5,3的倍数的特征”判断这个数是否有因数其次只要找到一个1和它本身以外的因数,就能肯定这个数是合数。如果除了1和它本身找不到其他因数,这个数就是质数。
一、复习回顾
二、基础练习
最小的质数是( ),最小的合数是( )。
2、5、8
4
( )既不是质数也不是合数。
1
2
要使四位数4□27是3 的倍数,方框里应填( )。
1.填空。
二、基础练习
自然数按是否是2 的倍数可分为( )和( )。
9和15
偶数
( )是所有非零自然数的因数。
1
奇数
20以内既是奇数又是合数的有( )。
1.填空。
二、基础练习
2.判断。
10÷2.5=4,所以10是2.5和4的倍数,2.5和4是10的因数。( )
如果a是b的最小倍数,则a=b。 ( )
奇数+偶数=奇数,奇数×偶数=奇数。 ( )
×
×
一个数的倍数一定大于它的因数。 ( )
一个合数至少有3个因数。 ( )
个位上是3、6、9的数是3的倍数。 ( )
×
√
×
√
我是一个偶数,也是一个两位数,十位数字与个位数字的积是18,我是多少呢?
1.猜数游戏。
答:36或92
三、强化练习
2. 分一分,填一填,并与同伴交流你的想法。
1 10 12 25 37 54 102 417 23 298
1
10
12
25
37
54
102
417
23
298
10
12
25
37
54
102
417
23
298
三、强化练习
3. 还有其他的包装方式吗?
6,5,3都是90的因数,所以每盒6瓶、5瓶、3瓶都正好装完。90的因数还有1,2,9,10,15,18,30,45,90。所以其他包装方式有每盒1瓶,2瓶,9瓶,10瓶,15瓶,18瓶,30瓶,45瓶,90瓶。
三、强化练习
4.选择题。
A质数 B合数 C奇数 D偶数
(1)两个质数的积一定是( )。
(2)两个合数的积一定是( )。
(3)当a是自然数时,2a+1一定是( )。
B
B
C
三、强化练习
A B C D E F G
A: 2的倍数;
B:最小的质数;
C: 既是奇数,又是合数;
D: 既不是质数,也不是合数
E: 最小的合数;
F: 既是2 的倍数,又是 3 的倍数;
G: 最大的因数是 5 。
8
2
9
1
4
6
5
A:2、4、6、8
B:2
C: 9
D: 1
E: 4
F: 6
G: 5
5.A、B、C、D、E、F、G分别代表不同的数字。
三、强化练习
哥德巴赫猜想(偶数情形):任何不小于4的偶数都可以写成两个质数相加的形式。
例如:4=2+2,6=3+3,8=3+5,…
哥德巴赫猜想
哥德巴赫猜想(奇数情形):任何不小于7的奇数都可以写成三个质数的和。
例如:7=2+2+3,9=2+2+5,…
对于哥德巴赫猜想的奇数情形,目前已经证明。
对于哥德巴赫猜想的偶数情形,目前最好的结果是我国数学家陈景润证明的结果:任何充分大的偶数都可以写成一个质数加上不超过两个质数的乘积的形式,通常称“1+2”。例如:50=17+3×11,16=2+2×7,…
四、拓展练习
10=( )+( )
11=( )+( )+( )
16=( )+( )
15=( )+( )+( )
40=( )+( )
21=( )+( )+( )
阅读了以上材料,请你在下面的括号里填上合适的质数。
四、拓展练习
3
7
3
13
3
37
5
5
11
3
5
7
2
2
7
再见
同课章节目录
- 一 小数除法
- 1 精打细算
- 2 打扫卫生
- 3 谁打电话的时间长
- 4 人民币兑换
- 5 除得尽吗
- 6 调查“生活垃圾”
- 二 轴对称和平移
- 1 轴对称再认识(一)
- 2 轴对称再认识(二)
- 3 平移
- 4 欣赏与设计
- 三 倍数与因数
- 1 倍数与因数
- 2 探索活动:2、5的倍数的特征
- 3 探索活动:3的倍数的特征
- 4 找因数
- 5 找质数
- 四 多边形的面积
- 1 比较图形的面积
- 2 认识底和高
- 3 探索活动:平行四边形的面积
- 4 探索活动:三角形的面积
- 5 探索活动:梯形的面积
- 五 分数的意义
- 1 分数的再认识(一)
- 2 分数的再认识(二)
- 3 分饼
- 4 分数与除法
- 5 分数基本性质
- 6 找最大的公因数
- 7 约分
- 8 找最小的公倍数
- 9 分数的大小
- 六 组合图形的面积
- 1 组合图形的面积
- 2 探索活动:成长的脚印
- 3 公顷、平方千米
- 数学好玩
- 1 设计秋游方案
- 2 图形中的规律
- 3 尝试与猜测
- 七 可能性
- 1 谁先走
- 2 摸球游戏
