2023年中考数学考点强化训练 函数基础知识(含解析)
文档属性
| 名称 | 2023年中考数学考点强化训练 函数基础知识(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 355.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-07 06:26:47 | ||
图片预览


文档简介
2023中考数学专题集训——函数基础知识
一、单选题
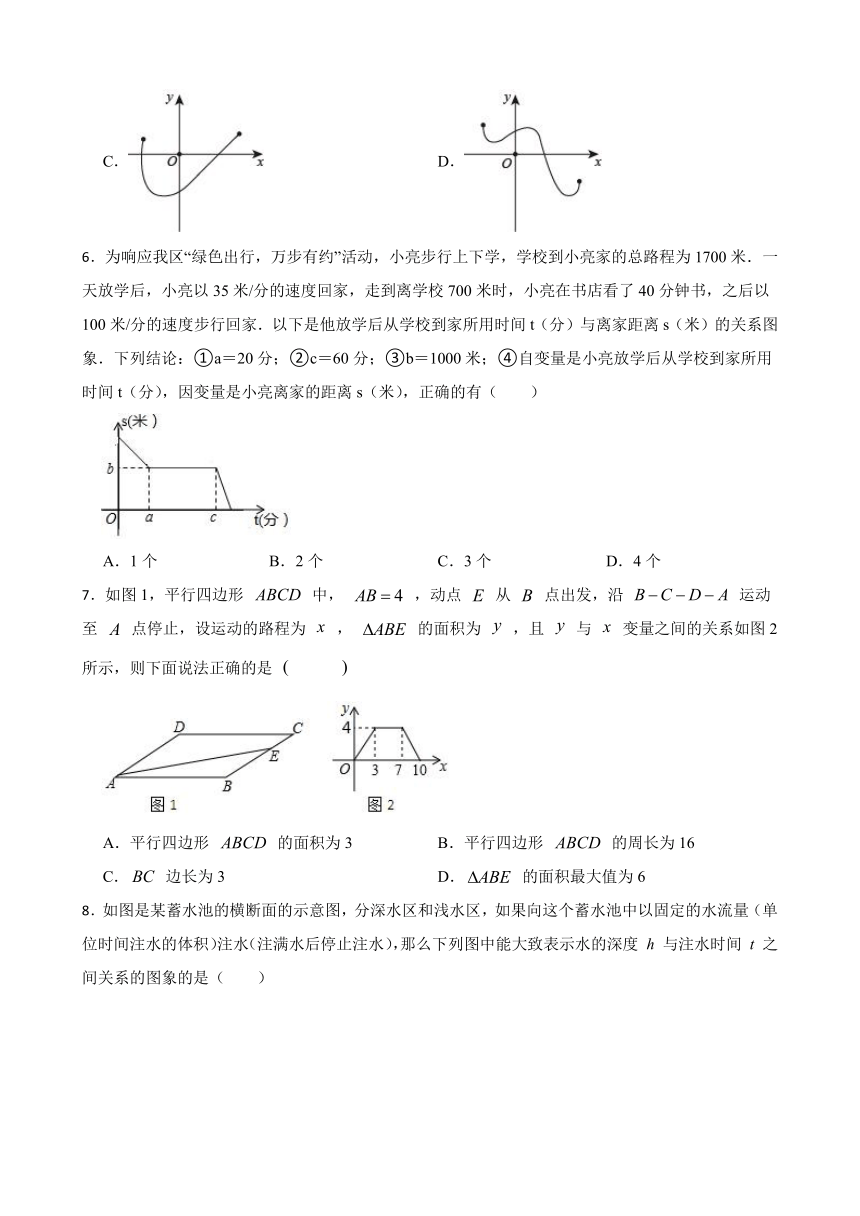
1.函数y=中自变量x的取值范围是( )
A.x≠﹣3 B.x≠3 C.x≤3 D.x≤﹣3
2.下列各图的直线或曲线中,不能表示是的函数的是( )
A. B.
C. D.
3.函数y=1- 的自变量x的取值范围是( )
A.x≤1 B.x≥-1 C.x>1 D.x≤0
4.如图,把两根木条AB和AC的一端A用螺栓固定在一起,木条AC自由转动至位置.在转动过程中,下面的量是常量的为( )
A.的度数 B.BC的长度
C.C的面积 D.AC的长度
5.下列曲线中,不表示是的函数图象的是( )
A. B.
C. D.
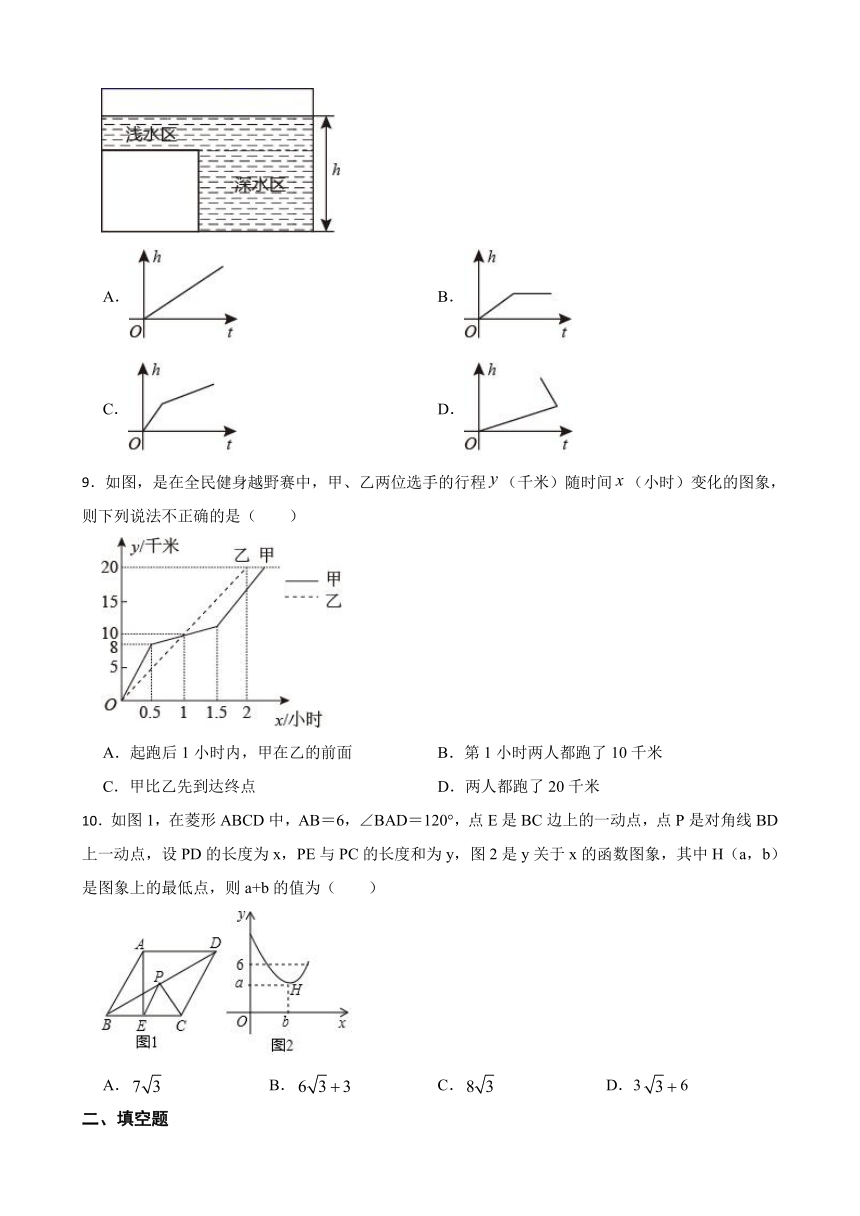
6.为响应我区“绿色出行,万步有约”活动,小亮步行上下学,学校到小亮家的总路程为1700米.一天放学后,小亮以35米/分的速度回家,走到离学校700米时,小亮在书店看了40分钟书,之后以100米/分的速度步行回家.以下是他放学后从学校到家所用时间t(分)与离家距离s(米)的关系图象.下列结论:①a=20分;②c=60分;③b=1000米;④自变量是小亮放学后从学校到家所用时间t(分),因变量是小亮离家的距离s(米),正确的有( )
A.1个 B.2个 C.3个 D.4个
7.如图1,平行四边形 中, ,动点 从 点出发,沿 运动至 点停止,设运动的路程为 , 的面积为 ,且 与 变量之间的关系如图2所示,则下面说法正确的是
A.平行四边形 的面积为3 B.平行四边形 的周长为16
C. 边长为3 D. 的面积最大值为6
8.如图是某蓄水池的横断面的示意图,分深水区和浅水区,如果向这个蓄水池中以固定的水流量(单位时间注水的体积)注水(注满水后停止注水),那么下列图中能大致表示水的深度 h 与注水时间 t 之间关系的图象的是( )
A. B.
C. D.
9.如图,是在全民健身越野赛中,甲、乙两位选手的行程(千米)随时间(小时)变化的图象,则下列说法不正确的是( )
A.起跑后1小时内,甲在乙的前面 B.第1小时两人都跑了10千米
C.甲比乙先到达终点 D.两人都跑了20千米
10.如图1,在菱形ABCD中,AB=6,∠BAD=120°,点E是BC边上的一动点,点P是对角线BD上一动点,设PD的长度为x,PE与PC的长度和为y,图2是y关于x的函数图象,其中H(a,b)是图象上的最低点,则a+b的值为( )
A. B. C. D.36
二、填空题
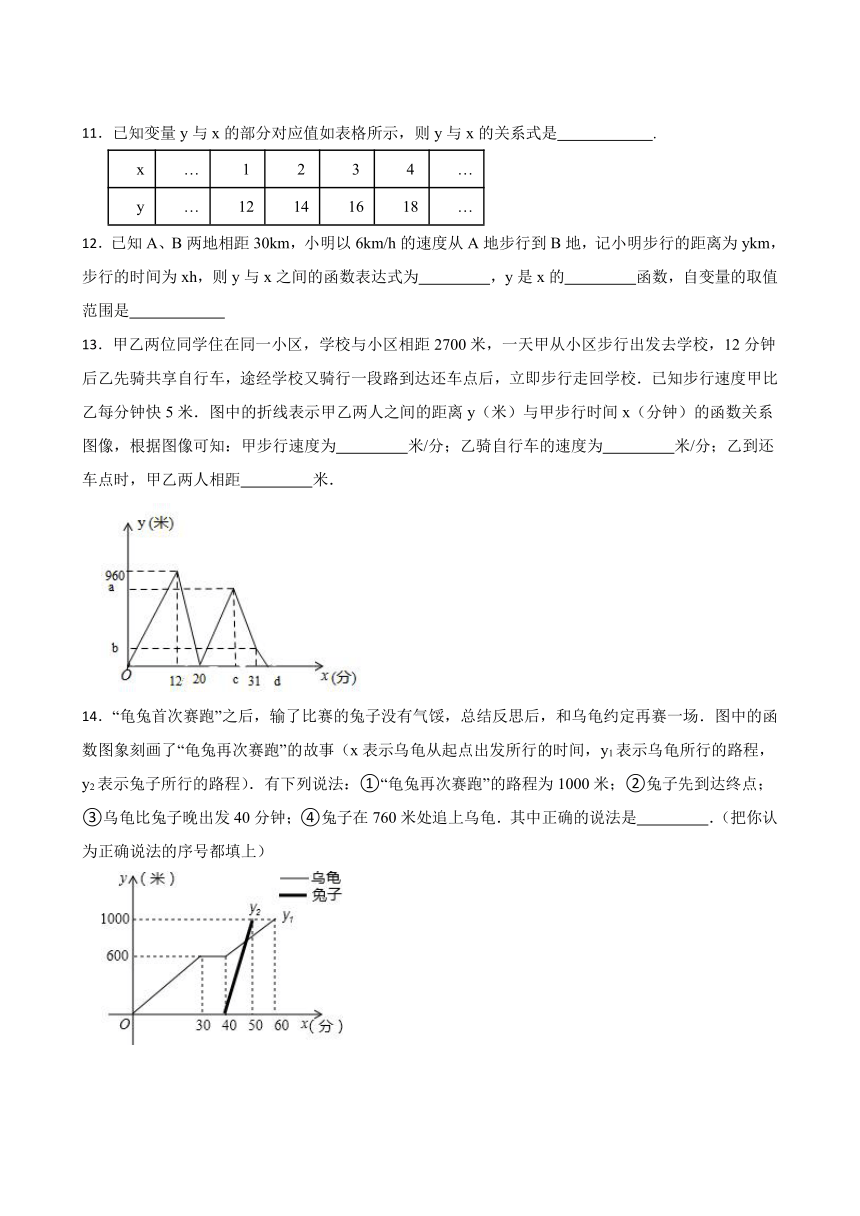
11.已知变量y与x的部分对应值如表格所示,则y与x的关系式是 .
x … 1 2 3 4 …
y … 12 14 16 18 …
12.已知A、B两地相距30km,小明以6km/h的速度从A地步行到B地,记小明步行的距离为ykm,步行的时间为xh,则y与x之间的函数表达式为 ,y是x的 函数,自变量的取值范围是
13.甲乙两位同学住在同一小区,学校与小区相距2700米,一天甲从小区步行出发去学校,12分钟后乙先骑共享自行车,途经学校又骑行一段路到达还车点后,立即步行走回学校.已知步行速度甲比乙每分钟快5米.图中的折线表示甲乙两人之间的距离y(米)与甲步行时间x(分钟)的函数关系图像,根据图像可知:甲步行速度为 米/分;乙骑自行车的速度为 米/分;乙到还车点时,甲乙两人相距 米.
14.“龟兔首次赛跑”之后,输了比赛的兔子没有气馁,总结反思后,和乌龟约定再赛一场.图中的函数图象刻画了“龟兔再次赛跑”的故事(x表示乌龟从起点出发所行的时间,y1表示乌龟所行的路程,y2表示兔子所行的路程).有下列说法:①“龟兔再次赛跑”的路程为1000米;②兔子先到达终点;③乌龟比兔子晚出发40分钟;④兔子在760米处追上乌龟.其中正确的说法是 .(把你认为正确说法的序号都填上)
三、解答题
15.在同一平面直角坐标系中画出正比例函数y=x和一次函数y=﹣x+2的图象,并求出这两个函数图象与x轴围成的三角形面积.
16.已知二次函数y=(x-1)2+n,当x=2时,y=2.求该二次函数的解析式,并在平面直角坐标系中画出该函数的图象.
17.已知y是x的一次函数,当x=3时,y=1;当x= 2时,y= 4,求这个一次函数的解析式.
18.甲、乙两车从A城出发前往B城,在整个行程中,甲车离开A城的距离 与甲车离开A城的时间 的对应关系如图所示.乙车比甲车晚出发 ,以 的速度匀速行驶.
(1)填空:
① 两城相距 ;
②当 时,甲车的速度为 ;
③乙车比甲车晚 到达 城;
④甲车出发 时,距离 城 ;
⑤甲、乙两车在行程中相遇时,甲车离开 城的时间为 ;
(2)当 时,请直接写出 关于 的函数解析式.
(3)当 时,两车所在位置的距离最多相差多少 ?
答案解析部分
1.【答案】B
【解析】【解答】解:由题意,得3﹣x≠0,
解得x≠3.
故答案为:B.
【分析】由分母不等于零,列出不等式3-x≠0,求解不等式即可得出答案.
2.【答案】B
【解析】【解答】解:A选项,对于x的每一个确定的值,y都有唯一的值与其对应,是函数,故该选项不符合题意;
B选项,对于x的每一个确定的值,y有可能有2个值与其对应,不是函数,故该选项符合题意;
C选项,对于x的每一个确定的值,y都有唯一的值与其对应,是函数,故该选项不符合题意;
D选项,对于x的每一个确定的值,y都有唯一的值与其对应,是函数,故该选项不符合题意.
故答案为:B.
【分析】在一个变化过程中,假设有两个变量x、y,如果对于任意一个x都有唯一确定的一个y和它对应,那么就称y是x的函数,据此判断.
3.【答案】B
【解析】【解答】解:∵x+1≥0,
∴x≥-1,
故答案为:B.
【分析】根据二次根式的被开方数大于等于0的条件,列出不等式求解即可.
4.【答案】D
【解析】【解答】∵木条AC再自由转动过程中,木条AC的长度始终保持不变,
∴AC的长度是常量。
故答案为:D。
【分析】根据常量的定义求解即可。
5.【答案】A
【解析】【解答】解:显然B、C、D选项中,对于自变量x的任何值,y都有唯一的值与之相对应,y是x的函数;
A选项对于x取值时,y可能有2个值与之相对应,则y不是x的函数;
故答案为:A.
【分析】根据函数定义:对于自变量x的任何值,y都有唯一的值与之相对应,y是x的函数,即可解得.
6.【答案】D
【解析】【解答】解:①a=700÷35=20(分钟),故①符合题意;
②20+40=60(分钟),故②符合题意;
③b=1700-700=1000(米),故③符合题意;
④由题意可知:该函数图象是小亮放学后从学校到家所用时间t(分)与离家距离s(米)的关系图象,
∴自变量为小亮放学后从学校到家所用时间t(分),因变量为小亮放学后离家的距离s(米),
故④符合题意,
故答案为:D.
【分析】根据题意和题目中的数据,可以计算出a、b、c的值,再根据自变量和因变量的定义判断即可。
7.【答案】C
【解析】【解答】解:由图2可得, , ,故 选项正确,符合题意;
平行四边形的周长为 ;故 选项错误,不符合题意;
当点 在 上运动时,三角形的面积不断增大,
最大面积 ;当点 在 上运动时,三角形的面积为定值4.故 选项错误,不符合题意.
当点 在 上运动时三角形的面不断减小,当点 与点 重合时,面积为0.
平行四边形的面积为8,故 选项错误,不符合题意.
故答案为:C.
【分析】由图2可得:BC=3,CD=4,求出平行四边形ABCD的周长,据此可判断BC;当点E在BC上运动时,三角形的面积不断增大,最大面积为4 ;当点E在DC上运动时,三角形的面积为定值4,据此判断D;当点E在AD上运动时三角形的面不断减小,当点E与点A重合时,面积为0,据此判断A.
8.【答案】C
【解析】【解答】解:∵在底面积不变的情况下,水的深度 h 与注水时间 t 之间是成正比例的,
∴在底面积不变的情况下,水的深度 h 与注水时间 t 之间是一次函数关系,
∴在底面积不变的情况下,水的深度 h 与注水时间 t 之间的图象是射线或线段,
∵深水区的底面积小于整个水池的底面积,
∴第一根线比第二根线要陡,并且两根线不会与坐标轴平行,
∴C图象是正确的,其他都是错误的,
故答案为:C.
【分析】根据题意可知:当底面积较小时,h随t的变化较快,当底面积较大时,h随t的变化较慢,即可得出答案。
9.【答案】C
【解析】【解答】解:由图象可知:
起跑后1小时内,甲的运动函数图象在乙的上方,所以甲在乙的前面,A说法不符合题意;
第1小时两人相遇,都跑了10千米,B说法不符合题意;
到达终点时,乙用时较短,所以应该是乙比甲先到达终点,C说法符合题意;
两人都跑了20千米,D说法不符合题意.
故答案为:C.
【分析】根据 时的函数图象判断出A正确;根据x=1时的y值判断出B正确;根据y=20时的x的值判断出C错误;根据函数图象y的值判断出D正确。
10.【答案】A
【解析】【解答】解:如下图,在边上取点,使得和关于对称,
连接,得,
连接,作,垂足为,
由三角形三边关系和垂线段最短知,
,
即有最小值,
菱形中,,,
在△中,,
解得,
是图象上的最低点
,
此时令与交于点,
由于,在△中,
,又,
,
又的长度为,图2中是图象上的最低点,
,
又,
,
故答案为:A.
【分析】在边上取点,使得和关于对称,由三角形三边关系和垂线段最短知,
,即有最小值,根据是图象上的最低点,得出b的值,此时令与交于点,再根据的长度为,图2中是图象上的最低点,得出a的值,由此得出答案。
11.【答案】y=2x+10
【解析】【解答】解:x每增加1,y增加2,易得当x=0时y=10,所以y=2x+10.
故答案为:y=2x+10.
【分析】由表格中的数据可得:x每增加1,y增加2,据此不难得到y与x的关系式.
12.【答案】y=6x;正比例;0≤x≤5
【解析】【解答】解:根据“路程= 速度x时间”可得y=6x.从表达式可知y是x的正比例函数.由于A、B两地相距30 km,小明的速度为6 km/h,所以小明最多步行5 h,故x的取值范围是0≤x≤5.
【分析】根据 A、B两地相距30km,小明以6km/h的速度从A地步行到B地, 求函数解析式,再求解即可。
13.【答案】80;200;840
【解析】【解答】解:由题意得:甲步行的速度为:960÷12=80(米/分),
乙骑自行车的速度为:80+960÷(20-12)=200(米/分),
乙步行的速度为:80-5=75(米/分),
乙全程:200(c-12)-75(31-c)=2700,解得c=27,
所以乙骑自行车的路程为:200×(27-12)=3000(米),
所以自行车还车点距离学校为:3000-2700=300(米),
乙到还车点时,乙的路程为3000米,
甲步行的路程为:80×27=2160(米),
此时两人相距:3000-2160=840(米).
故答案为:80,200,840
【分析】由图象知甲12分钟走了960米,利用速度=路程÷时间即得甲步行的速度;先求出甲乙的速度差,再加上80米/分,即得乙骑车的速度;乙步行的速度=乙骑车的速度-5,根据乙走完全程,可求出c值,由200×(c-12)可求出骑自行车的路程,再减去2700可得自行车还车点与学校的距离,然后利用乙到还车点时乙的路程减去甲步行的路程,即得两人相距的路程.
14.【答案】①②
【解析】【解答】由图像可得,“龟兔再次赛跑”的路程为1000米,
故①符合题意;
由图像可得,乌龟在60分的时候到达终点,兔子在50分的时候到达终点,
∴兔子先到达终点,
故②符合题意;
由图像可得,乌龟0分的时候出发,兔子40分的时候出发,
∴兔子比乌龟晚出发40分钟,
∴③不符合题意;
设y1=k1x+b(k1≠0)(40≤x≤60).
根据图示知,该直线经过点(40,600),(60,1000),
则,
解得,
所以该函数解析式为y1=20x-200(40≤x≤60),
同理,y2=100x-4000(40≤x≤50),
当y1=y2时,兔子追上乌龟,
此时20x-200=100x-4000,
解得:x=47.5,
∴y1=y2=750米,即兔子在途中750米处追上乌龟.
故④不符合题意.
∴正确的说法是①②.
故答案为:①②.
【分析】根据函数图象中的数据,可以直接判断出①②③,再根据函数图象中的数据,可以分别求出得当40≤x≤60时,y1与x的函数关系式和当40≤x≤50时,y2与x的函数关系式,然后理工它们的函数值相等,即可得到兔子在多少米处追上乌龟,从而可以判断④。
15.【答案】解:在同一平面直角坐标系中画出正比例函数y=x和一次函数y=-x+2的图象如下图:
则两函数图象互相垂直,
∵正比例函数y=x中,当y=0时,x=0,
一次函数y=-x+2中,当y=0时,x=2,当x=0时,y=2,
∴这两个函数图象与x轴围成的三角形面积为: .
【解析】【分析】先在同一平面直角坐标系中画出正比例函数 和一次函数的图象,即可求解两函数图象与坐标轴的交点坐标,进而利用三角形的面积公式计算可求解。
16.【答案】解:因为当 时, .
所以 .
解得
所以二次函数的解析式为:
列表得:
… -1 0 1 2 3 …
… 5 2 1 2 5 …
如图:
【解析】【分析】将x=2、y=2代入y=(x-1)2+n中可得n的值,即可得二次函数的解析式;然后利用列表、描点、连线即可作出函数的图象.
17.【答案】解:设这个一次函数的解析式为y="kx+b," 将x=3,y=1和x= 2,y= 4分别代入y=kx+b得,,
解这个方程组得,.
∴所求一次函数的解析式为y=x—2.
【解析】【分析】设这个一次函数的解析式为y=kx+b,分别将x=3,y=1和x= 2,y= 4分别代入y=kx+b得方程组,求出k、b的值,即可得到答案。
18.【答案】(1)360;60;;; 或
(2)当 时, ;
当 时, ;
当 时,代入( )、( )得 .
(3)当 时,
由题意,可知甲车在乙车前面,设两车所在位置的距离相差 ,
则 .
,
随 的增大而增大.
∴当 时, 取得最大值 .
答:两车所在位置的距离最多相差 .
【解析】【解答】(1)①根据图像可以读出距离为360km;
②120÷2=60;
③乙车需要360÷60=6小时, ;
④ ;
⑤第一次相遇:120÷60+ = ;
第二次相遇: ,解得 ;
【分析】根据函数图象和题意进行求解即可。
一、单选题
1.函数y=中自变量x的取值范围是( )
A.x≠﹣3 B.x≠3 C.x≤3 D.x≤﹣3
2.下列各图的直线或曲线中,不能表示是的函数的是( )
A. B.
C. D.
3.函数y=1- 的自变量x的取值范围是( )
A.x≤1 B.x≥-1 C.x>1 D.x≤0
4.如图,把两根木条AB和AC的一端A用螺栓固定在一起,木条AC自由转动至位置.在转动过程中,下面的量是常量的为( )
A.的度数 B.BC的长度
C.C的面积 D.AC的长度
5.下列曲线中,不表示是的函数图象的是( )
A. B.
C. D.
6.为响应我区“绿色出行,万步有约”活动,小亮步行上下学,学校到小亮家的总路程为1700米.一天放学后,小亮以35米/分的速度回家,走到离学校700米时,小亮在书店看了40分钟书,之后以100米/分的速度步行回家.以下是他放学后从学校到家所用时间t(分)与离家距离s(米)的关系图象.下列结论:①a=20分;②c=60分;③b=1000米;④自变量是小亮放学后从学校到家所用时间t(分),因变量是小亮离家的距离s(米),正确的有( )
A.1个 B.2个 C.3个 D.4个
7.如图1,平行四边形 中, ,动点 从 点出发,沿 运动至 点停止,设运动的路程为 , 的面积为 ,且 与 变量之间的关系如图2所示,则下面说法正确的是
A.平行四边形 的面积为3 B.平行四边形 的周长为16
C. 边长为3 D. 的面积最大值为6
8.如图是某蓄水池的横断面的示意图,分深水区和浅水区,如果向这个蓄水池中以固定的水流量(单位时间注水的体积)注水(注满水后停止注水),那么下列图中能大致表示水的深度 h 与注水时间 t 之间关系的图象的是( )
A. B.
C. D.
9.如图,是在全民健身越野赛中,甲、乙两位选手的行程(千米)随时间(小时)变化的图象,则下列说法不正确的是( )
A.起跑后1小时内,甲在乙的前面 B.第1小时两人都跑了10千米
C.甲比乙先到达终点 D.两人都跑了20千米
10.如图1,在菱形ABCD中,AB=6,∠BAD=120°,点E是BC边上的一动点,点P是对角线BD上一动点,设PD的长度为x,PE与PC的长度和为y,图2是y关于x的函数图象,其中H(a,b)是图象上的最低点,则a+b的值为( )
A. B. C. D.36
二、填空题
11.已知变量y与x的部分对应值如表格所示,则y与x的关系式是 .
x … 1 2 3 4 …
y … 12 14 16 18 …
12.已知A、B两地相距30km,小明以6km/h的速度从A地步行到B地,记小明步行的距离为ykm,步行的时间为xh,则y与x之间的函数表达式为 ,y是x的 函数,自变量的取值范围是
13.甲乙两位同学住在同一小区,学校与小区相距2700米,一天甲从小区步行出发去学校,12分钟后乙先骑共享自行车,途经学校又骑行一段路到达还车点后,立即步行走回学校.已知步行速度甲比乙每分钟快5米.图中的折线表示甲乙两人之间的距离y(米)与甲步行时间x(分钟)的函数关系图像,根据图像可知:甲步行速度为 米/分;乙骑自行车的速度为 米/分;乙到还车点时,甲乙两人相距 米.
14.“龟兔首次赛跑”之后,输了比赛的兔子没有气馁,总结反思后,和乌龟约定再赛一场.图中的函数图象刻画了“龟兔再次赛跑”的故事(x表示乌龟从起点出发所行的时间,y1表示乌龟所行的路程,y2表示兔子所行的路程).有下列说法:①“龟兔再次赛跑”的路程为1000米;②兔子先到达终点;③乌龟比兔子晚出发40分钟;④兔子在760米处追上乌龟.其中正确的说法是 .(把你认为正确说法的序号都填上)
三、解答题
15.在同一平面直角坐标系中画出正比例函数y=x和一次函数y=﹣x+2的图象,并求出这两个函数图象与x轴围成的三角形面积.
16.已知二次函数y=(x-1)2+n,当x=2时,y=2.求该二次函数的解析式,并在平面直角坐标系中画出该函数的图象.
17.已知y是x的一次函数,当x=3时,y=1;当x= 2时,y= 4,求这个一次函数的解析式.
18.甲、乙两车从A城出发前往B城,在整个行程中,甲车离开A城的距离 与甲车离开A城的时间 的对应关系如图所示.乙车比甲车晚出发 ,以 的速度匀速行驶.
(1)填空:
① 两城相距 ;
②当 时,甲车的速度为 ;
③乙车比甲车晚 到达 城;
④甲车出发 时,距离 城 ;
⑤甲、乙两车在行程中相遇时,甲车离开 城的时间为 ;
(2)当 时,请直接写出 关于 的函数解析式.
(3)当 时,两车所在位置的距离最多相差多少 ?
答案解析部分
1.【答案】B
【解析】【解答】解:由题意,得3﹣x≠0,
解得x≠3.
故答案为:B.
【分析】由分母不等于零,列出不等式3-x≠0,求解不等式即可得出答案.
2.【答案】B
【解析】【解答】解:A选项,对于x的每一个确定的值,y都有唯一的值与其对应,是函数,故该选项不符合题意;
B选项,对于x的每一个确定的值,y有可能有2个值与其对应,不是函数,故该选项符合题意;
C选项,对于x的每一个确定的值,y都有唯一的值与其对应,是函数,故该选项不符合题意;
D选项,对于x的每一个确定的值,y都有唯一的值与其对应,是函数,故该选项不符合题意.
故答案为:B.
【分析】在一个变化过程中,假设有两个变量x、y,如果对于任意一个x都有唯一确定的一个y和它对应,那么就称y是x的函数,据此判断.
3.【答案】B
【解析】【解答】解:∵x+1≥0,
∴x≥-1,
故答案为:B.
【分析】根据二次根式的被开方数大于等于0的条件,列出不等式求解即可.
4.【答案】D
【解析】【解答】∵木条AC再自由转动过程中,木条AC的长度始终保持不变,
∴AC的长度是常量。
故答案为:D。
【分析】根据常量的定义求解即可。
5.【答案】A
【解析】【解答】解:显然B、C、D选项中,对于自变量x的任何值,y都有唯一的值与之相对应,y是x的函数;
A选项对于x取值时,y可能有2个值与之相对应,则y不是x的函数;
故答案为:A.
【分析】根据函数定义:对于自变量x的任何值,y都有唯一的值与之相对应,y是x的函数,即可解得.
6.【答案】D
【解析】【解答】解:①a=700÷35=20(分钟),故①符合题意;
②20+40=60(分钟),故②符合题意;
③b=1700-700=1000(米),故③符合题意;
④由题意可知:该函数图象是小亮放学后从学校到家所用时间t(分)与离家距离s(米)的关系图象,
∴自变量为小亮放学后从学校到家所用时间t(分),因变量为小亮放学后离家的距离s(米),
故④符合题意,
故答案为:D.
【分析】根据题意和题目中的数据,可以计算出a、b、c的值,再根据自变量和因变量的定义判断即可。
7.【答案】C
【解析】【解答】解:由图2可得, , ,故 选项正确,符合题意;
平行四边形的周长为 ;故 选项错误,不符合题意;
当点 在 上运动时,三角形的面积不断增大,
最大面积 ;当点 在 上运动时,三角形的面积为定值4.故 选项错误,不符合题意.
当点 在 上运动时三角形的面不断减小,当点 与点 重合时,面积为0.
平行四边形的面积为8,故 选项错误,不符合题意.
故答案为:C.
【分析】由图2可得:BC=3,CD=4,求出平行四边形ABCD的周长,据此可判断BC;当点E在BC上运动时,三角形的面积不断增大,最大面积为4 ;当点E在DC上运动时,三角形的面积为定值4,据此判断D;当点E在AD上运动时三角形的面不断减小,当点E与点A重合时,面积为0,据此判断A.
8.【答案】C
【解析】【解答】解:∵在底面积不变的情况下,水的深度 h 与注水时间 t 之间是成正比例的,
∴在底面积不变的情况下,水的深度 h 与注水时间 t 之间是一次函数关系,
∴在底面积不变的情况下,水的深度 h 与注水时间 t 之间的图象是射线或线段,
∵深水区的底面积小于整个水池的底面积,
∴第一根线比第二根线要陡,并且两根线不会与坐标轴平行,
∴C图象是正确的,其他都是错误的,
故答案为:C.
【分析】根据题意可知:当底面积较小时,h随t的变化较快,当底面积较大时,h随t的变化较慢,即可得出答案。
9.【答案】C
【解析】【解答】解:由图象可知:
起跑后1小时内,甲的运动函数图象在乙的上方,所以甲在乙的前面,A说法不符合题意;
第1小时两人相遇,都跑了10千米,B说法不符合题意;
到达终点时,乙用时较短,所以应该是乙比甲先到达终点,C说法符合题意;
两人都跑了20千米,D说法不符合题意.
故答案为:C.
【分析】根据 时的函数图象判断出A正确;根据x=1时的y值判断出B正确;根据y=20时的x的值判断出C错误;根据函数图象y的值判断出D正确。
10.【答案】A
【解析】【解答】解:如下图,在边上取点,使得和关于对称,
连接,得,
连接,作,垂足为,
由三角形三边关系和垂线段最短知,
,
即有最小值,
菱形中,,,
在△中,,
解得,
是图象上的最低点
,
此时令与交于点,
由于,在△中,
,又,
,
又的长度为,图2中是图象上的最低点,
,
又,
,
故答案为:A.
【分析】在边上取点,使得和关于对称,由三角形三边关系和垂线段最短知,
,即有最小值,根据是图象上的最低点,得出b的值,此时令与交于点,再根据的长度为,图2中是图象上的最低点,得出a的值,由此得出答案。
11.【答案】y=2x+10
【解析】【解答】解:x每增加1,y增加2,易得当x=0时y=10,所以y=2x+10.
故答案为:y=2x+10.
【分析】由表格中的数据可得:x每增加1,y增加2,据此不难得到y与x的关系式.
12.【答案】y=6x;正比例;0≤x≤5
【解析】【解答】解:根据“路程= 速度x时间”可得y=6x.从表达式可知y是x的正比例函数.由于A、B两地相距30 km,小明的速度为6 km/h,所以小明最多步行5 h,故x的取值范围是0≤x≤5.
【分析】根据 A、B两地相距30km,小明以6km/h的速度从A地步行到B地, 求函数解析式,再求解即可。
13.【答案】80;200;840
【解析】【解答】解:由题意得:甲步行的速度为:960÷12=80(米/分),
乙骑自行车的速度为:80+960÷(20-12)=200(米/分),
乙步行的速度为:80-5=75(米/分),
乙全程:200(c-12)-75(31-c)=2700,解得c=27,
所以乙骑自行车的路程为:200×(27-12)=3000(米),
所以自行车还车点距离学校为:3000-2700=300(米),
乙到还车点时,乙的路程为3000米,
甲步行的路程为:80×27=2160(米),
此时两人相距:3000-2160=840(米).
故答案为:80,200,840
【分析】由图象知甲12分钟走了960米,利用速度=路程÷时间即得甲步行的速度;先求出甲乙的速度差,再加上80米/分,即得乙骑车的速度;乙步行的速度=乙骑车的速度-5,根据乙走完全程,可求出c值,由200×(c-12)可求出骑自行车的路程,再减去2700可得自行车还车点与学校的距离,然后利用乙到还车点时乙的路程减去甲步行的路程,即得两人相距的路程.
14.【答案】①②
【解析】【解答】由图像可得,“龟兔再次赛跑”的路程为1000米,
故①符合题意;
由图像可得,乌龟在60分的时候到达终点,兔子在50分的时候到达终点,
∴兔子先到达终点,
故②符合题意;
由图像可得,乌龟0分的时候出发,兔子40分的时候出发,
∴兔子比乌龟晚出发40分钟,
∴③不符合题意;
设y1=k1x+b(k1≠0)(40≤x≤60).
根据图示知,该直线经过点(40,600),(60,1000),
则,
解得,
所以该函数解析式为y1=20x-200(40≤x≤60),
同理,y2=100x-4000(40≤x≤50),
当y1=y2时,兔子追上乌龟,
此时20x-200=100x-4000,
解得:x=47.5,
∴y1=y2=750米,即兔子在途中750米处追上乌龟.
故④不符合题意.
∴正确的说法是①②.
故答案为:①②.
【分析】根据函数图象中的数据,可以直接判断出①②③,再根据函数图象中的数据,可以分别求出得当40≤x≤60时,y1与x的函数关系式和当40≤x≤50时,y2与x的函数关系式,然后理工它们的函数值相等,即可得到兔子在多少米处追上乌龟,从而可以判断④。
15.【答案】解:在同一平面直角坐标系中画出正比例函数y=x和一次函数y=-x+2的图象如下图:
则两函数图象互相垂直,
∵正比例函数y=x中,当y=0时,x=0,
一次函数y=-x+2中,当y=0时,x=2,当x=0时,y=2,
∴这两个函数图象与x轴围成的三角形面积为: .
【解析】【分析】先在同一平面直角坐标系中画出正比例函数 和一次函数的图象,即可求解两函数图象与坐标轴的交点坐标,进而利用三角形的面积公式计算可求解。
16.【答案】解:因为当 时, .
所以 .
解得
所以二次函数的解析式为:
列表得:
… -1 0 1 2 3 …
… 5 2 1 2 5 …
如图:
【解析】【分析】将x=2、y=2代入y=(x-1)2+n中可得n的值,即可得二次函数的解析式;然后利用列表、描点、连线即可作出函数的图象.
17.【答案】解:设这个一次函数的解析式为y="kx+b," 将x=3,y=1和x= 2,y= 4分别代入y=kx+b得,,
解这个方程组得,.
∴所求一次函数的解析式为y=x—2.
【解析】【分析】设这个一次函数的解析式为y=kx+b,分别将x=3,y=1和x= 2,y= 4分别代入y=kx+b得方程组,求出k、b的值,即可得到答案。
18.【答案】(1)360;60;;; 或
(2)当 时, ;
当 时, ;
当 时,代入( )、( )得 .
(3)当 时,
由题意,可知甲车在乙车前面,设两车所在位置的距离相差 ,
则 .
,
随 的增大而增大.
∴当 时, 取得最大值 .
答:两车所在位置的距离最多相差 .
【解析】【解答】(1)①根据图像可以读出距离为360km;
②120÷2=60;
③乙车需要360÷60=6小时, ;
④ ;
⑤第一次相遇:120÷60+ = ;
第二次相遇: ,解得 ;
【分析】根据函数图象和题意进行求解即可。
同课章节目录
