北师大版数学八年级下册 6.2.1 平行四边形的判定(第1课时)课件(共14张PPT)
文档属性
| 名称 | 北师大版数学八年级下册 6.2.1 平行四边形的判定(第1课时)课件(共14张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-07 08:15:46 | ||
图片预览






文档简介
(共14张PPT)
数学八年级下册 BS
第 六 章 平行四边形
2 平行四边形的判定
第1课时
问题思考
平行四边形具有什么性质
①平行四边形是中心对称图形,两条对角线的交点是它的对称中心.
②边:平行四边形的对边相等.
③角:平行四边形的对角相等.
④对角线:平行四边形的对角线互相平分.
学习新知
现在同学们拿出每人准备好的两根等长的小木条,两个同学合作,把一个人的相等的两根小木条作为一个四边形的一组对边,另一个同学的作为四边形的另一组对边,组成一个四边形,能行吗
平行四边形的判定定理
【活动1】
工具:两对长度分别相等的木条.
动手:能否在平面内用这四根木条摆成一个平行四边形
【思考1】 你能说明你所摆出的四边形是平行四边形吗
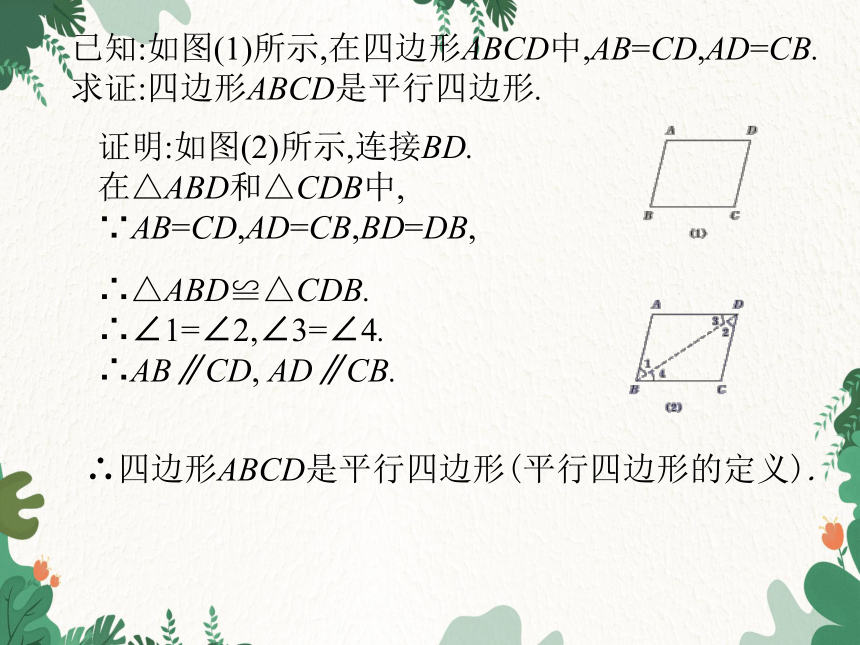
已知:如图(1)所示,在四边形ABCD中,AB=CD,AD=CB.
求证:四边形ABCD是平行四边形.
证明:如图(2)所示,连接BD.
在△ABD和△CDB中,
∵AB=CD,AD=CB,BD=DB,
∴△ABD≌△CDB.
∴∠1=∠2,∠3=∠4.
∴AB∥CD, AD∥CB.
∴四边形ABCD是平行四边形(平行四边形的定义).
平行四边形的判定定理:两组对边分别相等的四边形是平行四边形.
【思考2】 以上活动事实,能用文字语言表达吗
【活动2】
工具:两根长度相等的木条,两条平行线.
动手:利用两根长度相等的木条能摆出以木条顶端为顶点的平行四边形吗
【思考1】 你能说明你所摆出的四边形是平行四边形吗
已知:如图(1)所示,在四边形ABCD中,AB CD.
求证:四边形ABCD是平行四边形.
证明:如图(2)所示,连接AC.
∵AB∥CD,
∴∠BAC=∠DCA.
又∵AB=CD, AC=CA,
∴△ABC≌△CDA.
∴BC=DA.
∴四边形ABCD是平行四边形(两组对边分别相等的四边形是平行四边形).
平行四边形的判定定理:一组对边平行且相等的四边形是平行四边形.
【思考2】 以上活动事实,能用文字语言表达吗
例1 已知:如图所示,在 □ ABCD中,E,F分别为AD和CB的中点.
求证:四边形BFDE是平行四边形.
【解析】 本例是对平行四边形性质和判定的综合应用.要证明一个四边形是平行四边形,
除了依据平行四边形的定义外,还可以考虑本课时刚学完的两个平行四边形的判定定理.
证明:∵四边形ABCD是平行四边形,
∴AD=CB(平行四边形的对边相等),
AD∥CB(平行四边形的定义).
∵E,F分别是AD和CB的中点,
∴ED= AD,FB= CB.
∴ED=FB,ED∥FB.
1.四边形ABCD中,对角线AC与BD交于点O,下列条件中不能判定这个四边形是平行四边形的是 ( )
A.OA=OC,OB=OD B.AD∥BC,AB∥CD
C.AB=CD,AD=BC D.AB∥DC,AD=BC
D
2.如图所示,在四边形ABCD中,AB∥CD,要使得四边形ABCD是平行四边形,应添加的条件是 .(只填写一个条件,不使用图形以外的字母和线段)
AB= CD(答案不唯一)
检测反馈
3.如图所示,在□ ABCD中,点E,F分别在边AD,BC上,且BE∥DF,若∠EBF= 45°,则∠EDF的度数是 度.
【解析】由四边形ABCD是平行四边形,可得AD∥BC,又由BE∥DF,即可证得四边形BFDE是平行四边形,根据平行四边形的对角相等,即可求得∠EDF=∠EBF=45°.故填45.
45
4.如图所示,四边形ABCD是平行四边形,DE平分∠ADC交AB于点E,BF平分∠ABC交CD于点F.
(1)求证DE=BF;
(2)连接EF,写出图中所有的全等三角形.(不要求证明)
证明:(1)∵四边形ABCD是平行四边形,
∴DC∥AB,∴∠CDE=∠AED.
∵DE平分∠ADC,∴∠ADE=∠CDE,
∴∠ADE=∠AED,∴AE=AD.
同理CF=CB.
又AD=CB,∴CF=AE,∴DF=BE,
∴四边形DEBF是平行四边形,∴DE=BF.
解:(2)△ADE≌△CBF,
△DFE≌△BEF.
数学八年级下册 BS
第 六 章 平行四边形
2 平行四边形的判定
第1课时
问题思考
平行四边形具有什么性质
①平行四边形是中心对称图形,两条对角线的交点是它的对称中心.
②边:平行四边形的对边相等.
③角:平行四边形的对角相等.
④对角线:平行四边形的对角线互相平分.
学习新知
现在同学们拿出每人准备好的两根等长的小木条,两个同学合作,把一个人的相等的两根小木条作为一个四边形的一组对边,另一个同学的作为四边形的另一组对边,组成一个四边形,能行吗
平行四边形的判定定理
【活动1】
工具:两对长度分别相等的木条.
动手:能否在平面内用这四根木条摆成一个平行四边形
【思考1】 你能说明你所摆出的四边形是平行四边形吗
已知:如图(1)所示,在四边形ABCD中,AB=CD,AD=CB.
求证:四边形ABCD是平行四边形.
证明:如图(2)所示,连接BD.
在△ABD和△CDB中,
∵AB=CD,AD=CB,BD=DB,
∴△ABD≌△CDB.
∴∠1=∠2,∠3=∠4.
∴AB∥CD, AD∥CB.
∴四边形ABCD是平行四边形(平行四边形的定义).
平行四边形的判定定理:两组对边分别相等的四边形是平行四边形.
【思考2】 以上活动事实,能用文字语言表达吗
【活动2】
工具:两根长度相等的木条,两条平行线.
动手:利用两根长度相等的木条能摆出以木条顶端为顶点的平行四边形吗
【思考1】 你能说明你所摆出的四边形是平行四边形吗
已知:如图(1)所示,在四边形ABCD中,AB CD.
求证:四边形ABCD是平行四边形.
证明:如图(2)所示,连接AC.
∵AB∥CD,
∴∠BAC=∠DCA.
又∵AB=CD, AC=CA,
∴△ABC≌△CDA.
∴BC=DA.
∴四边形ABCD是平行四边形(两组对边分别相等的四边形是平行四边形).
平行四边形的判定定理:一组对边平行且相等的四边形是平行四边形.
【思考2】 以上活动事实,能用文字语言表达吗
例1 已知:如图所示,在 □ ABCD中,E,F分别为AD和CB的中点.
求证:四边形BFDE是平行四边形.
【解析】 本例是对平行四边形性质和判定的综合应用.要证明一个四边形是平行四边形,
除了依据平行四边形的定义外,还可以考虑本课时刚学完的两个平行四边形的判定定理.
证明:∵四边形ABCD是平行四边形,
∴AD=CB(平行四边形的对边相等),
AD∥CB(平行四边形的定义).
∵E,F分别是AD和CB的中点,
∴ED= AD,FB= CB.
∴ED=FB,ED∥FB.
1.四边形ABCD中,对角线AC与BD交于点O,下列条件中不能判定这个四边形是平行四边形的是 ( )
A.OA=OC,OB=OD B.AD∥BC,AB∥CD
C.AB=CD,AD=BC D.AB∥DC,AD=BC
D
2.如图所示,在四边形ABCD中,AB∥CD,要使得四边形ABCD是平行四边形,应添加的条件是 .(只填写一个条件,不使用图形以外的字母和线段)
AB= CD(答案不唯一)
检测反馈
3.如图所示,在□ ABCD中,点E,F分别在边AD,BC上,且BE∥DF,若∠EBF= 45°,则∠EDF的度数是 度.
【解析】由四边形ABCD是平行四边形,可得AD∥BC,又由BE∥DF,即可证得四边形BFDE是平行四边形,根据平行四边形的对角相等,即可求得∠EDF=∠EBF=45°.故填45.
45
4.如图所示,四边形ABCD是平行四边形,DE平分∠ADC交AB于点E,BF平分∠ABC交CD于点F.
(1)求证DE=BF;
(2)连接EF,写出图中所有的全等三角形.(不要求证明)
证明:(1)∵四边形ABCD是平行四边形,
∴DC∥AB,∴∠CDE=∠AED.
∵DE平分∠ADC,∴∠ADE=∠CDE,
∴∠ADE=∠AED,∴AE=AD.
同理CF=CB.
又AD=CB,∴CF=AE,∴DF=BE,
∴四边形DEBF是平行四边形,∴DE=BF.
解:(2)△ADE≌△CBF,
△DFE≌△BEF.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
