苏教版数学六年级下册 第四单元 比例-第三课时 比例的基本性质课件(共22张PPT)
文档属性
| 名称 | 苏教版数学六年级下册 第四单元 比例-第三课时 比例的基本性质课件(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-06 15:01:52 | ||
图片预览






文档简介
(共22张PPT)
六年级数学下册教学课件(苏教版)
第四单元 比例
第三课时 比例的基本性质
目 录
情景导学
1
探索与发现
2
学以致用
3
课后作业
4
情景导学
01
情景导学
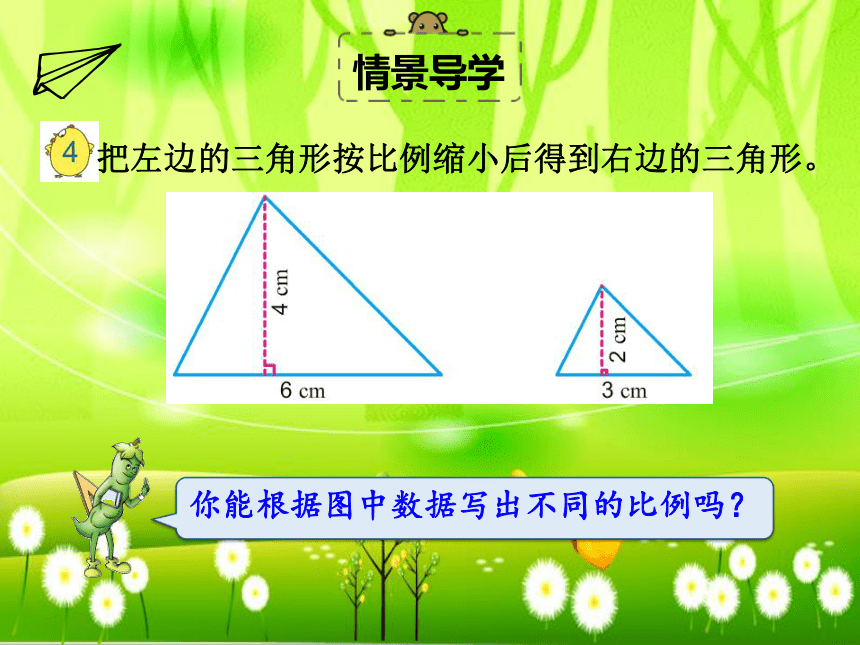
把左边的三角形按比例缩小后得到右边的三角形。
你能根据图中数据写出不同的比例吗?
探索与发现
02
探索与发现
6 ∶3 = 4 ∶ 2
两个三角形高的比
和底的比相等。
两个三角形底的比
和高的比相等。
每个三角形底和
高的比相等。
每个三角形高和
底的比相等。
4 ∶ 2 = 6 ∶ 3
6 ∶ 4 = 3 ∶ 2
4 ∶ 6 = 2 ∶ 3
探索与发现
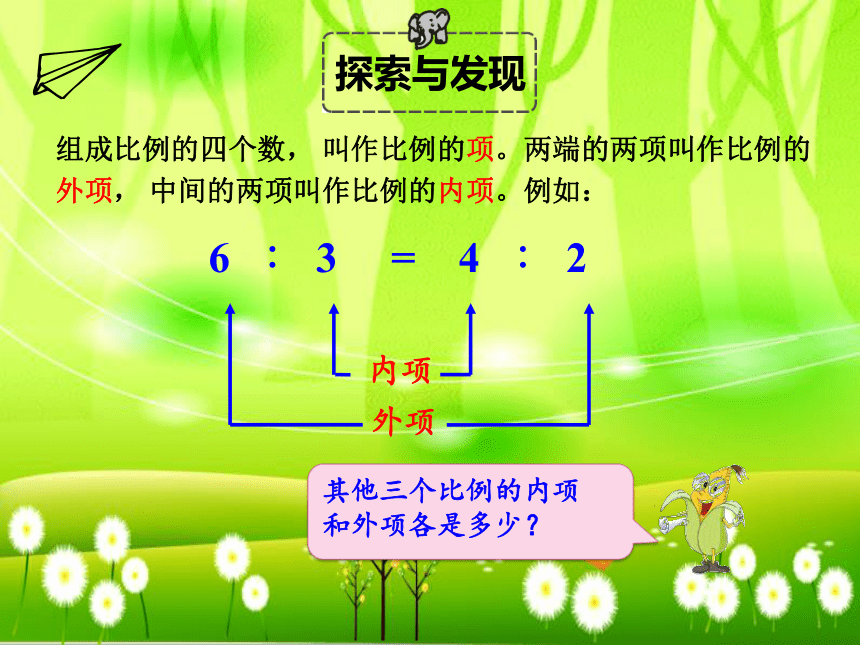
组成比例的四个数, 叫作比例的项。两端的两项叫作比例的外项, 中间的两项叫作比例的内项。例如:
6 ∶ 3 = 4 ∶ 2
外项
内项
其他三个比例的内项
和外项各是多少?
探索与发现
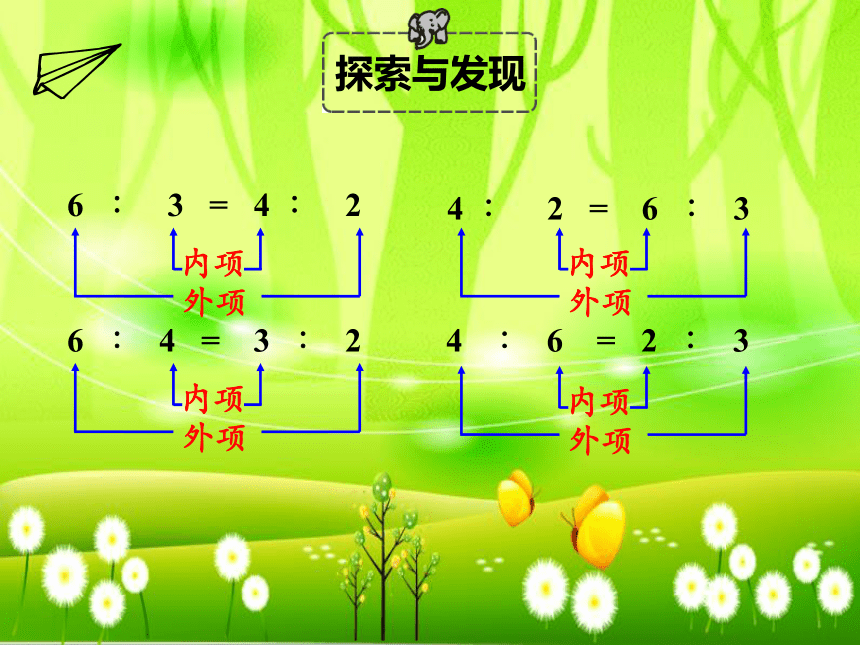
6 ∶ 3 = 4 ∶ 2
4 ∶ 2 = 6 ∶ 3
6 ∶ 4 = 3 ∶ 2
4 ∶ 6 = 2 ∶ 3
外项
内项
外项
内项
外项
内项
外项
内项
探索与发现
观察上面的四个比例, 你有什么发现?
6和2可以同时是比例的外项, 也可以同时是比例的内项。
6×2=3×4,两个外项的积与两个内项的积相等。
3和4 可以同时是比例的内项, 也可以同时是比例的外项。
再写出一些比例, 看看是不是有同样的规律。
探索与发现
如果用字母表示比例的四个项, 即a:b=c:d,那么这个规律可以表示成:a × d = b × c
6 : 3 = 4 : 2
4 : 2 = 6 : 3
6 : 4 = 3 : 2
4 : 6 = 2 : 3
外项
内项
外项
内项
外项
内项
外项
内项
探索与发现
在比例里, 两个外项的积等于两个内项的积, 这叫作比例的基本性质。
如果用字母表示比例的四个项,即a:b=c:d,那么这个规律可以表示成:
a × d = b × c
探索与发现
如果把比例写成分数形式,把等号两端的分子、分母交叉相乘,结果怎样?
6×2=3×4
如果用字母表示比例的四个项, 即a:b = c:d,那么这个规律可以表示成:
a × d = b × c
探索与发现
应用比例的基本性质,判断下面每组的两个比能否组成比例。如果能组成比例,把组成的比例写出来。
3.6 ∶1.8 和0.5 ∶ 0.25 和18 ∶ 24
( )×( )=( ) ( )×( )=( )
( )×( )=( ) ( )×( )=( )
3.6
0.25
1.8
0.5
0.9
0.9
24
8
18
3.6:1.8 =0.5:0.25
不能组成比例
学以致用
03
学以致用
1. 一列火车从甲城开往乙城,行驶速度和所需时间如下表:
(1)从表中选择两组数据,写出一个乘积相等的式子。
80 6 120 4
120 4 160 3
学以致用
1. 一列火车从甲城开往乙城,行驶速度和所需时间如下表:
(2)根据上面的等式, 写出一个比例。
80 120 4 6
120 160 3 4
学以致用
2. 根据比例的基本性质, 在括号里填上合适的数。
3 8
4 10
学以致用
3.应用比例的基本性质,判断哪两个比可以组成比例。
6∶3和8∶5 0.2∶2.5和4∶50
0.2∶2.5=4∶50
学以致用
到现在为止,我们学习了判断两个比能否组成比例有几种方法?
两种方法:
1.看两个比的比值是否相等;
2.两个比的两个外项之积是否等于两个比的内项之积。
课后作业
04
完成教材课后习题及练习册同步练习。
课后作业
感 谢 观 看
六年级数学下册教学课件(苏教版)
第四单元 比例
第三课时 比例的基本性质
目 录
情景导学
1
探索与发现
2
学以致用
3
课后作业
4
情景导学
01
情景导学
把左边的三角形按比例缩小后得到右边的三角形。
你能根据图中数据写出不同的比例吗?
探索与发现
02
探索与发现
6 ∶3 = 4 ∶ 2
两个三角形高的比
和底的比相等。
两个三角形底的比
和高的比相等。
每个三角形底和
高的比相等。
每个三角形高和
底的比相等。
4 ∶ 2 = 6 ∶ 3
6 ∶ 4 = 3 ∶ 2
4 ∶ 6 = 2 ∶ 3
探索与发现
组成比例的四个数, 叫作比例的项。两端的两项叫作比例的外项, 中间的两项叫作比例的内项。例如:
6 ∶ 3 = 4 ∶ 2
外项
内项
其他三个比例的内项
和外项各是多少?
探索与发现
6 ∶ 3 = 4 ∶ 2
4 ∶ 2 = 6 ∶ 3
6 ∶ 4 = 3 ∶ 2
4 ∶ 6 = 2 ∶ 3
外项
内项
外项
内项
外项
内项
外项
内项
探索与发现
观察上面的四个比例, 你有什么发现?
6和2可以同时是比例的外项, 也可以同时是比例的内项。
6×2=3×4,两个外项的积与两个内项的积相等。
3和4 可以同时是比例的内项, 也可以同时是比例的外项。
再写出一些比例, 看看是不是有同样的规律。
探索与发现
如果用字母表示比例的四个项, 即a:b=c:d,那么这个规律可以表示成:a × d = b × c
6 : 3 = 4 : 2
4 : 2 = 6 : 3
6 : 4 = 3 : 2
4 : 6 = 2 : 3
外项
内项
外项
内项
外项
内项
外项
内项
探索与发现
在比例里, 两个外项的积等于两个内项的积, 这叫作比例的基本性质。
如果用字母表示比例的四个项,即a:b=c:d,那么这个规律可以表示成:
a × d = b × c
探索与发现
如果把比例写成分数形式,把等号两端的分子、分母交叉相乘,结果怎样?
6×2=3×4
如果用字母表示比例的四个项, 即a:b = c:d,那么这个规律可以表示成:
a × d = b × c
探索与发现
应用比例的基本性质,判断下面每组的两个比能否组成比例。如果能组成比例,把组成的比例写出来。
3.6 ∶1.8 和0.5 ∶ 0.25 和18 ∶ 24
( )×( )=( ) ( )×( )=( )
( )×( )=( ) ( )×( )=( )
3.6
0.25
1.8
0.5
0.9
0.9
24
8
18
3.6:1.8 =0.5:0.25
不能组成比例
学以致用
03
学以致用
1. 一列火车从甲城开往乙城,行驶速度和所需时间如下表:
(1)从表中选择两组数据,写出一个乘积相等的式子。
80 6 120 4
120 4 160 3
学以致用
1. 一列火车从甲城开往乙城,行驶速度和所需时间如下表:
(2)根据上面的等式, 写出一个比例。
80 120 4 6
120 160 3 4
学以致用
2. 根据比例的基本性质, 在括号里填上合适的数。
3 8
4 10
学以致用
3.应用比例的基本性质,判断哪两个比可以组成比例。
6∶3和8∶5 0.2∶2.5和4∶50
0.2∶2.5=4∶50
学以致用
到现在为止,我们学习了判断两个比能否组成比例有几种方法?
两种方法:
1.看两个比的比值是否相等;
2.两个比的两个外项之积是否等于两个比的内项之积。
课后作业
04
完成教材课后习题及练习册同步练习。
课后作业
感 谢 观 看
