认识不等式[下学期]
图片预览







文档简介
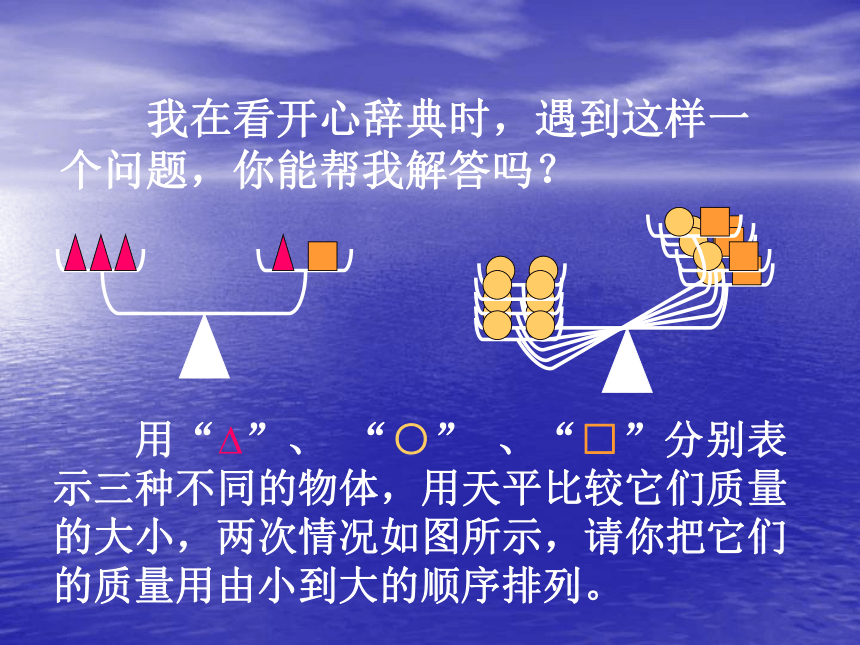
课件21张PPT。认识不等式第8章 一元一次不等式 在生活中,涉及到数学的问题很多,我们外出时常常见到这样的一些标志。你知道这些图标的意义是什么吗? 我在看开心辞典时,遇到这样一个问题,你能帮我解答吗? 用“?”、 “○” 、“□”分别表示三种不同的物体,用天平比较它们质量的大小,两次情况如图所示,请你把它们的质量用由小到大的顺序排列。世纪公园世纪公园的票价是:每人5元,一次购票满30张,每张票可少收1元. 公园的票价是:每人5元;一次购票满30张,每张可少收1元。某班有27人去世纪公园进行活动。当班长王小华准备好了零钱到售票处买27张票时,爱动脑筋的李敏喊住了王小华,提议买30张票。但有同学不明白,明明我们只有27个人,买30张票,岂不是“浪费”吗?那么,李敏的提议对不对呢?是不是真的浪费?
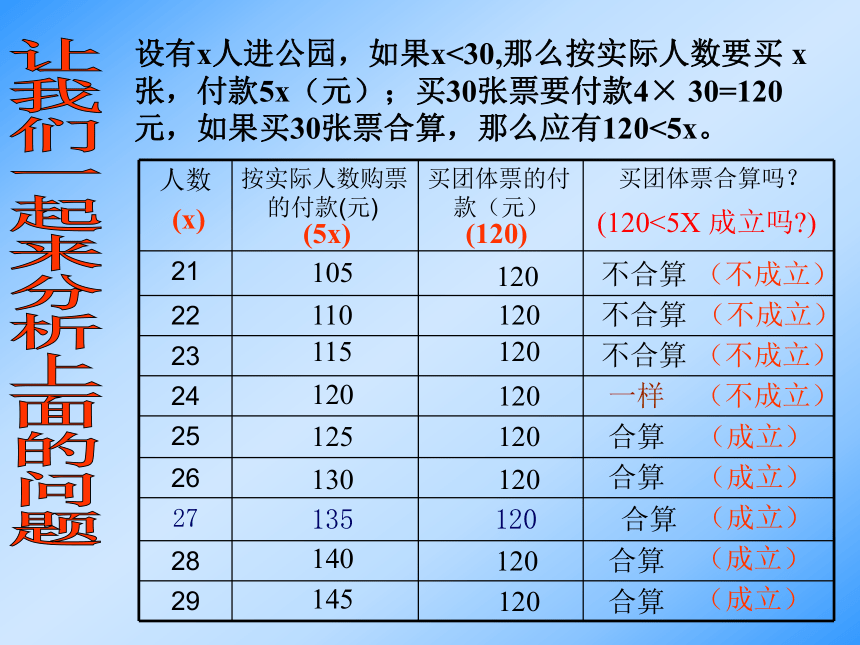
谈谈你的看法。买27张票,要付款买30张票,要付款显然 120<135我们不妨一起来算一算:5×27=135(元)4×30=120(元)问题这就是说,买30张票比买27张票付款要少,表面上看是“浪费”了3张票,实际上反而节省了。 如果去世纪公园的人数较少(例如10个人)显然不值得去买30张票,还是按实际人数买票为好。现在的问题是,少于30人时,至少有多少人去公园,买30张票反而合算呢?探索设有x人进公园,如果x<30,那么按实际人数要买 x张,付款5x(元);买30张票要付款4× 30=120元,如果买30张票合算,那么应有120<5x。105120不合算110120不合算115120不合算120120一样125120合算130120合算140120合算145120合算让我们一起来分析上面的问题(x) (5x)(120)(120<5X 成立吗?)(不成立)(不成立)(不成立)(不成立)(成立)(成立)(成立)(成立)(成立) 由上表可见,当x= ___________时,不等式120<5x成立,也就是说至少要x=_____时不等式120<5x成立,至少要有____人进公园时,买30张票反而合算. 25,26,……2525“≥”表示“不小于”(大于或等于), “≤”表示“不大于”(小于或等于)。像上面出现的 120<135,30>27,120<5x ,x<30那样有不等号“<”或“>”表示不等关系的式子,叫做不等式。注:不等号有:<、>、≠、≤、≥。【概 括】 不等式120<5x中含有未知数x,能使不等式成立的未知数的值, 叫做不等式的解。如上例中,x=25,26,27,…等都是120<5x的解,而x=24,23,22,21则都不是不等式的解。【概 括】注:不等式的解可以有无数个。当 机 立 断 判断下列各式中哪些是不等式,哪些不是?
(1) x+1=2 (2) 5x-3>1
(3) x-6 (4) 11x-4≤6
(5) 7>4 (6) 2x-y≥0
(7)-4<x<4是不是不是是是是是聪明的一休 判断下列各数,哪些是不等式x+2>5的解?哪些不是?⑴-3 ⑵-2 ⑶-1 ⑷ 0
⑸ 1.5 ⑹ 2.5 ⑺ 3
⑻ 3.5 ⑼ 5 (10)7 检验一个数是不是不等式的解,应代入不等式中检验.不是是是是不是不是不是不是不是不是不等式的解与一元一次方程的解有什么区别?注意:不等式的解与一元一次方程的解是有区别的.一元一次方程的解一般是一个具体的数值;而不等式的解通常不只一个,如上例中,x=25,26,27,…等都是120<5x的解,而x=24,23,22,21则都不是不等式的解。(1)x的一半不小于-1;(2)y与4的和大于0.5; (3)a是负数; (4)b是非负数; 解: (1) 0.5x≥-1,如x=-1,2;(2) y+4>0.5,如y=0,1;(3) a<0,如a=-3, -4; b是非负数,就是b不是负数,它可以是正
数或零,即b>0或b=0,通常可以表示成b≥ 0.
如b=0,2. 例: 用不等式表示下列关系,并写出两个满足不等式的数:你聪明吗?用不等式表示:
(1) x的3倍大于5;
(3) x的2倍大于x;
(5) a是正数; (1) 3x>5;
(3) 2x>x;
(5) a>0;
解:(2) y与2的差小于-1;
(4) y的1/2与3的差是负数;
(6) b不是正数.(2)y-2<-1;
(4)y/2-3<0;
(6)b≤0.1.已知不等式-4< x<4(1)写出6个满足不等式-4< x<4的x值,你能写出多少个这样的x值?
(2)写出这个不等式所有的整数解;
(3)求出此不等式的非负整数解。 2.写出一个含有a的不等式,使2是它的一个解。 某高速公路工地需要实施爆破,操作人员点燃导火线后,要在炸药爆炸前跑到200m以外的安全区域.已知导火线的燃烧速度是0.02m/s,人跑开的速度是5m/s,求导火线的长x(m)应满足的关系式。动脑一刻【思考】向阳小队10人到学校图书馆参加装订杂志的劳动,开始两天,每人每天完成5本杂志。问以后3天,每人每天必须完成几本杂志,才能超额完成300本杂志的装订任务?试列出不等式,找出符合题意的一些解。收获季节通过这节课你学到了什么?小 结1. 生活中处处存在不等关系,我们可以用不等式来解决生活中的实际问题;
2. 检验一个数是不是不等式的解,应代入不等式中检验;
3. 注意:不等式的解与一元一次方程的解是有区别的.一元一次方程的解一般是一个具体的数值,而不等式的解通常不只一个;
4. 在解题过程中,一定要注意“负数”、“非负数”、“大于”、“小于”、“不小于”等关键性词语,只有真正理解其含义,才能正确列出不等式。再见!
谈谈你的看法。买27张票,要付款买30张票,要付款显然 120<135我们不妨一起来算一算:5×27=135(元)4×30=120(元)问题这就是说,买30张票比买27张票付款要少,表面上看是“浪费”了3张票,实际上反而节省了。 如果去世纪公园的人数较少(例如10个人)显然不值得去买30张票,还是按实际人数买票为好。现在的问题是,少于30人时,至少有多少人去公园,买30张票反而合算呢?探索设有x人进公园,如果x<30,那么按实际人数要买 x张,付款5x(元);买30张票要付款4× 30=120元,如果买30张票合算,那么应有120<5x。105120不合算110120不合算115120不合算120120一样125120合算130120合算140120合算145120合算让我们一起来分析上面的问题(x) (5x)(120)(120<5X 成立吗?)(不成立)(不成立)(不成立)(不成立)(成立)(成立)(成立)(成立)(成立) 由上表可见,当x= ___________时,不等式120<5x成立,也就是说至少要x=_____时不等式120<5x成立,至少要有____人进公园时,买30张票反而合算. 25,26,……2525“≥”表示“不小于”(大于或等于), “≤”表示“不大于”(小于或等于)。像上面出现的 120<135,30>27,120<5x ,x<30那样有不等号“<”或“>”表示不等关系的式子,叫做不等式。注:不等号有:<、>、≠、≤、≥。【概 括】 不等式120<5x中含有未知数x,能使不等式成立的未知数的值, 叫做不等式的解。如上例中,x=25,26,27,…等都是120<5x的解,而x=24,23,22,21则都不是不等式的解。【概 括】注:不等式的解可以有无数个。当 机 立 断 判断下列各式中哪些是不等式,哪些不是?
(1) x+1=2 (2) 5x-3>1
(3) x-6 (4) 11x-4≤6
(5) 7>4 (6) 2x-y≥0
(7)-4<x<4是不是不是是是是是聪明的一休 判断下列各数,哪些是不等式x+2>5的解?哪些不是?⑴-3 ⑵-2 ⑶-1 ⑷ 0
⑸ 1.5 ⑹ 2.5 ⑺ 3
⑻ 3.5 ⑼ 5 (10)7 检验一个数是不是不等式的解,应代入不等式中检验.不是是是是不是不是不是不是不是不是不等式的解与一元一次方程的解有什么区别?注意:不等式的解与一元一次方程的解是有区别的.一元一次方程的解一般是一个具体的数值;而不等式的解通常不只一个,如上例中,x=25,26,27,…等都是120<5x的解,而x=24,23,22,21则都不是不等式的解。(1)x的一半不小于-1;(2)y与4的和大于0.5; (3)a是负数; (4)b是非负数; 解: (1) 0.5x≥-1,如x=-1,2;(2) y+4>0.5,如y=0,1;(3) a<0,如a=-3, -4; b是非负数,就是b不是负数,它可以是正
数或零,即b>0或b=0,通常可以表示成b≥ 0.
如b=0,2. 例: 用不等式表示下列关系,并写出两个满足不等式的数:你聪明吗?用不等式表示:
(1) x的3倍大于5;
(3) x的2倍大于x;
(5) a是正数; (1) 3x>5;
(3) 2x>x;
(5) a>0;
解:(2) y与2的差小于-1;
(4) y的1/2与3的差是负数;
(6) b不是正数.(2)y-2<-1;
(4)y/2-3<0;
(6)b≤0.1.已知不等式-4< x<4(1)写出6个满足不等式-4< x<4的x值,你能写出多少个这样的x值?
(2)写出这个不等式所有的整数解;
(3)求出此不等式的非负整数解。 2.写出一个含有a的不等式,使2是它的一个解。 某高速公路工地需要实施爆破,操作人员点燃导火线后,要在炸药爆炸前跑到200m以外的安全区域.已知导火线的燃烧速度是0.02m/s,人跑开的速度是5m/s,求导火线的长x(m)应满足的关系式。动脑一刻【思考】向阳小队10人到学校图书馆参加装订杂志的劳动,开始两天,每人每天完成5本杂志。问以后3天,每人每天必须完成几本杂志,才能超额完成300本杂志的装订任务?试列出不等式,找出符合题意的一些解。收获季节通过这节课你学到了什么?小 结1. 生活中处处存在不等关系,我们可以用不等式来解决生活中的实际问题;
2. 检验一个数是不是不等式的解,应代入不等式中检验;
3. 注意:不等式的解与一元一次方程的解是有区别的.一元一次方程的解一般是一个具体的数值,而不等式的解通常不只一个;
4. 在解题过程中,一定要注意“负数”、“非负数”、“大于”、“小于”、“不小于”等关键性词语,只有真正理解其含义,才能正确列出不等式。再见!
