沪科版八年级数学下册试题 20.1 数据的频数分布(含答案)
文档属性
| 名称 | 沪科版八年级数学下册试题 20.1 数据的频数分布(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 168.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-07 10:17:22 | ||
图片预览

文档简介
20.1 数据的频数分布
一、选择题.
1.下列六个数:0、、、π、﹣、中,无理数出现的频数是( )
A.3 B.4 C.5 D.6
2.将50个数据分成5组列出频数分布表,其中第一组的频数为6,第二组与第五组的频数和为20,第三组的频率为0.2,则第四组的频率为( )
A.4 B.14 C.0.28 D.50
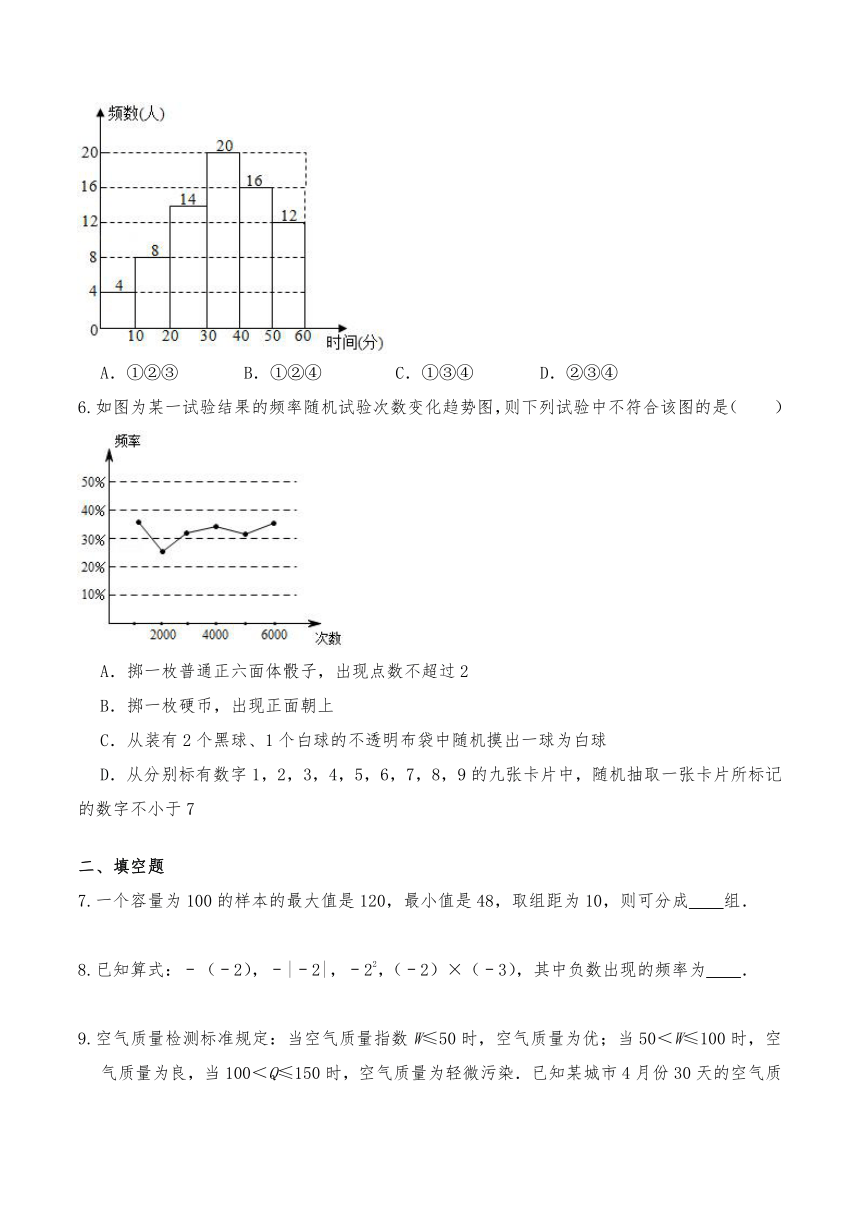
3.如图是某组15名学生数学测试成绩的频数分布直方图,则成绩低于60分的人数是( )
A.3人 B.6人 C.10人 D.14人
4.下列说法错误的是( )
A.随着试验次数的增多,某一事件发生的频率就会不断增大
B.一个事件A试验中出现的次数越多,频数就越大
C.试验的总次数一定时,频率与频数成正比
D.频数与频率都能反映一个事件出现的频繁程度
5.小文同学统计了他所在小区部分居民每天微信阅读的时间,绘制了直方图.得出了如下结论:①样本中每天阅读微信的时间没人超过1小时,由此可以断定这个小区的居民每天阅读微信时间超过1小时的很少;②样本中每天微信阅读不足20分钟的人数大约占16%;③选取样本的样本容量是60;④估计所有居民每天微信阅读35分钟以上的人数大约占总居民数的一半左右.其中正确的是( )
A.①②③ B.①②④ C.①③④ D.②③④
6.如图为某一试验结果的频率随机试验次数变化趋势图,则下列试验中不符合该图的是( )
A.掷一枚普通正六面体骰子,出现点数不超过2
B.掷一枚硬币,出现正面朝上
C.从装有2个黑球、1个白球的不透明布袋中随机摸出一球为白球
D.从分别标有数字1,2,3,4,5,6,7,8,9的九张卡片中,随机抽取一张卡片所标记的数字不小于7
二、填空题
7.一个容量为100的样本的最大值是120,最小值是48,取组距为10,则可分成 组.
已知算式:﹣(﹣2),﹣|﹣2|,﹣22,(﹣2)×(﹣3),其中负数出现的频率为 .
9.空气质量检测标准规定:当空气质量指数W≤50时,空气质量为优;当50<W≤100时,空气质量为良,当100<Q≤150时,空气质量为轻微污染.已知某城市4月份30天的空气质量状况,统计如表:
空气质量指数(W) 40 60 90 110 120 140
天数 3 5 10 7 4 1
这个月中,空气质量为良的天数的频率为 .
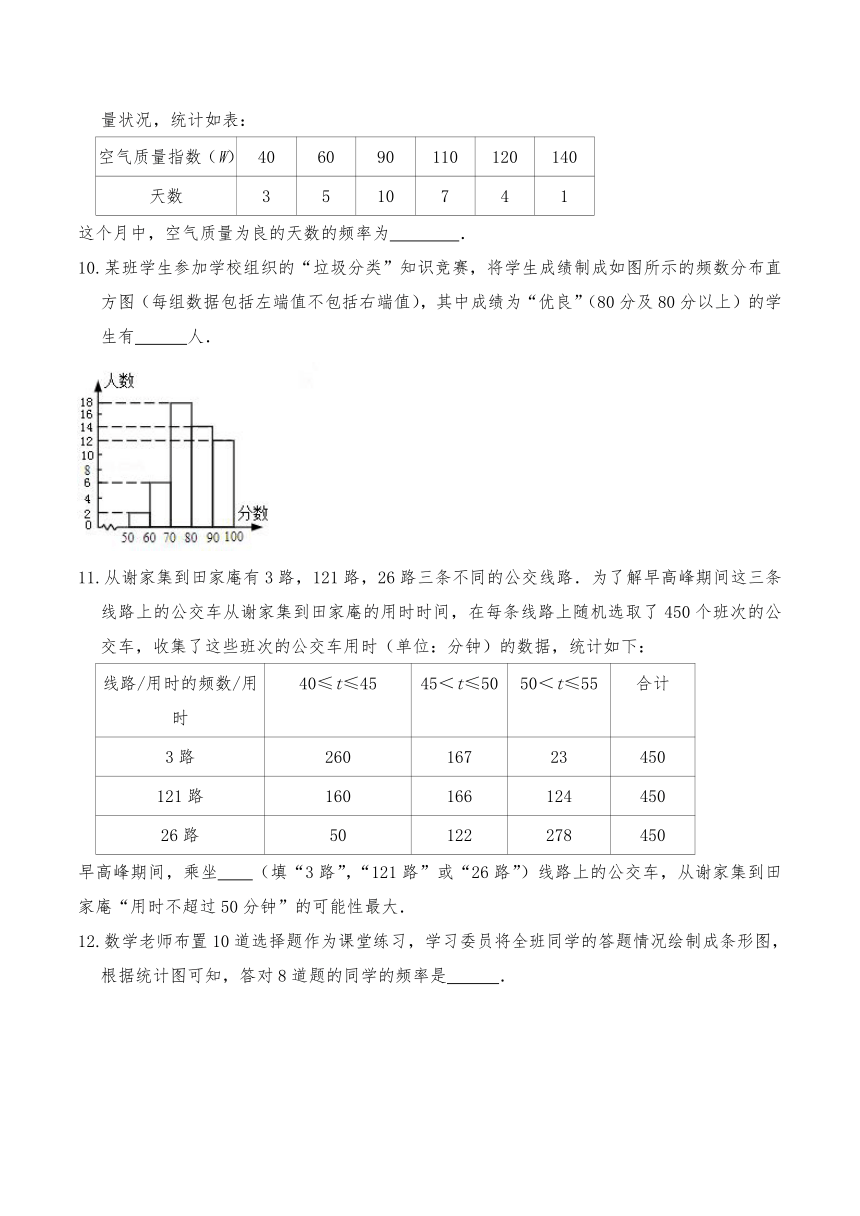
10.某班学生参加学校组织的“垃圾分类”知识竞赛,将学生成绩制成如图所示的频数分布直方图(每组数据包括左端值不包括右端值),其中成绩为“优良”(80分及80分以上)的学生有 人.
11.从谢家集到田家庵有3路,121路,26路三条不同的公交线路.为了解早高峰期间这三条线路上的公交车从谢家集到田家庵的用时时间,在每条线路上随机选取了450个班次的公交车,收集了这些班次的公交车用时(单位:分钟)的数据,统计如下:
线路/用时的频数/用时 40≤t≤45 45<t≤50 50<t≤55 合计
3路 260 167 23 450
121路 160 166 124 450
26路 50 122 278 450
早高峰期间,乘坐 (填“3路”,“121路”或“26路”)线路上的公交车,从谢家集到田家庵“用时不超过50分钟”的可能性最大.
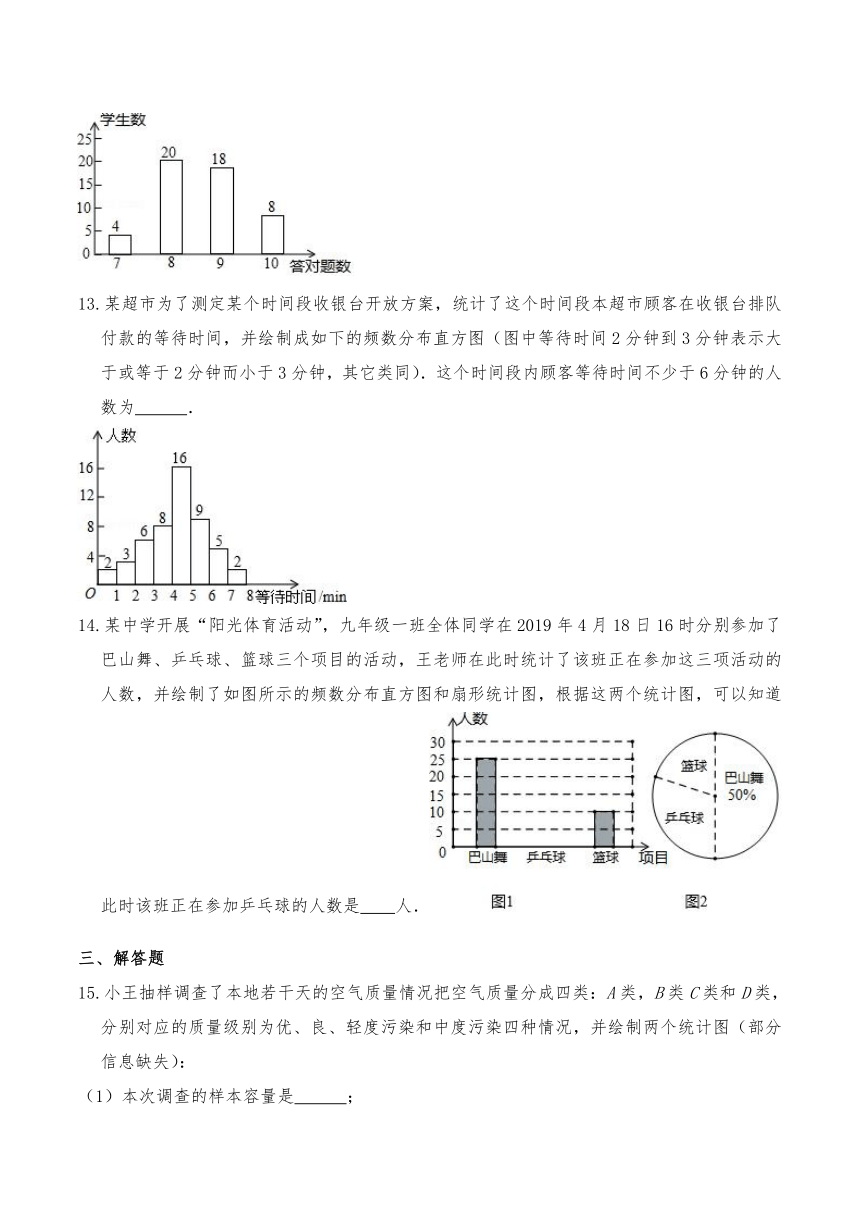
12.数学老师布置10道选择题作为课堂练习,学习委员将全班同学的答题情况绘制成条形图,根据统计图可知,答对8道题的同学的频率是 .
13.某超市为了测定某个时间段收银台开放方案,统计了这个时间段本超市顾客在收银台排队付款的等待时间,并绘制成如下的频数分布直方图(图中等待时间2分钟到3分钟表示大于或等于2分钟而小于3分钟,其它类同).这个时间段内顾客等待时间不少于6分钟的人数为 .
14.某中学开展“阳光体育活动”,九年级一班全体同学在2019年4月18日16时分别参加了巴山舞、乒乓球、篮球三个项目的活动,王老师在此时统计了该班正在参加这三项活动的人数,并绘制了如图所示的频数分布直方图和扇形统计图,根据这两个统计图,可以知道此时该班正在参加乒乓球的人数是 人.
三、解答题
15.小王抽样调查了本地若干天的空气质量情况把空气质量分成四类:A类,B类C类和D类,分别对应的质量级别为优、良、轻度污染和中度污染四种情况,并绘制两个统计图(部分信息缺失):
(1)本次调查的样本容量是 ;
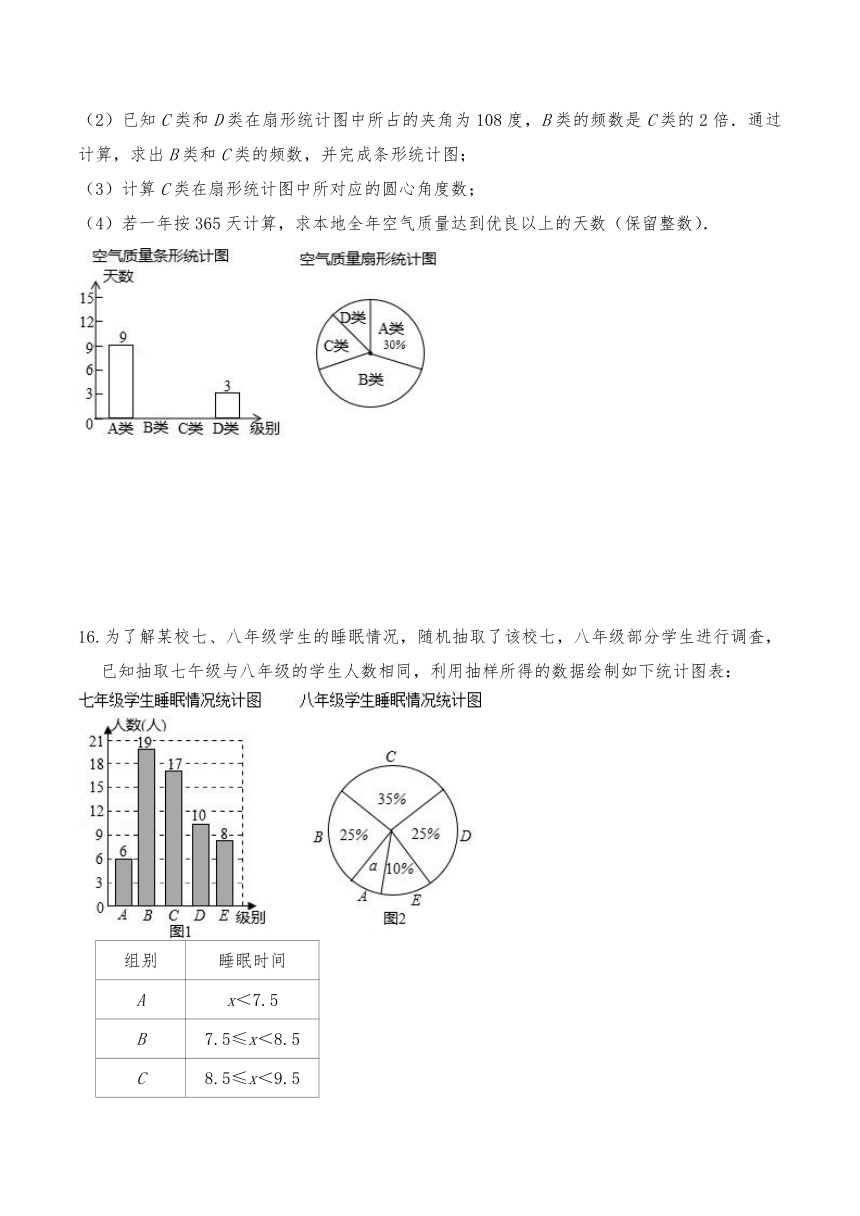
(2)已知C类和D类在扇形统计图中所占的夹角为108度,B类的频数是C类的2倍.通过计算,求出B类和C类的频数,并完成条形统计图;
(3)计算C类在扇形统计图中所对应的圆心角度数;
(4)若一年按365天计算,求本地全年空气质量达到优良以上的天数(保留整数).
16.为了解某校七、八年级学生的睡眠情况,随机抽取了该校七,八年级部分学生进行调査,已知抽取七午级与八年级的学生人数相同,利用抽样所得的数据绘制如下统计图表:
组别 睡眠时间
A x<7.5
B 7.5≤x<8.5
C 8.5≤x<9.5
D 9.5≤x<10.5
E x≥10.5
根据图表提供的信息,回答下列问题:
(1)扇形统计图中的a= ;
(2)抽取的样本中,八年级学生睡眠时间在C组的有多少人?
(3)已知该校七年级学生有755人,八年级学生有785人,如果睡眠吋间x(时)满足7.5≤x<8.5,称睡眠时间合格,试估计该校七、八年级学生中睡眠时间合格的共有多少人?
17.有一学校为了解九年级学生某次体育测试成绩,现对这次体育测试成绩进行随机抽样调查,结果统计如下,其中扇形统计图中C等级所在扇形的圆心角为36°.
被抽取的体育测试成绩频数分布表
等级 成绩(分) 频数(人数)
A 36<x≤40 19
B 32<x≤36 b
C 28<x≤32 5
D 24<x≤28 4
E 20<x≤24 2
合计 a
请你根据以上图表提供的信息,解答下列问题:
(1)a= ,b= ;
(2)A等级的频率是 ;
(3)在扇形统计图中,B等级所对应的圆心角是 度.
18.随着移动终端设备的升级换代,手机已经成为我们生活中不可缺少的一部分,为了解中学生在假期使用
手机的情况(选项:A.和同学亲友聊天;B.学习;C.购物;D.游戏;E.其它),端午节后某中学在全校范围内随机抽取了若干名学生进行调查,得到如右表格(部分信息未给出):
根据以上信息解答下列问题:
选项 频数 频率
A 10 M
B N 0.2
C 5 0.1
D P 0.4
E 5 0.1
(1)这次被调查的学生有多少人?
(2)求表中m,n的值;
(3)若该中学有800名学生,估计全校学生中利用手机购物或玩游戏的共有多少人?
19.为增强学生垃圾分类意识,推动垃圾分类进校园.某初中学校组织全校1200名学生参加了“垃圾分类知识竞赛”,为了解学生的答题情况,学校考虑采用简单随机抽样的方法抽取部分学生的成绩进行调查分析.
(1)学校设计了以下三种抽样调查方案:
方案一:从初一、初二、初三年级中指定部分学生成绩作为样本进行调查分析;
方案二:从初一、初二年级中随机抽取部分男生成绩及在初三年级中随机抽取部分女生成绩进行调查分析;
方案三:从三个年级全体学生中随机抽取部分学生成绩进行调查分析.
其中抽取的样本具有代表性的方案是 .(填“方案一”、“方案二”或“方案三”)
(2)学校根据样本数据,绘制成下表(90分及以上为“优秀”,60分及以上为“及格”):
样本容量 平均分 及格率 优秀率 最高分 最低分
100 93.5 100% 70% 100 80
分数段统计(学生成绩记为x)
分数段 0≤x<80 80≤x<85 85≤x<90 90≤x<95 95≤x≤100
频数 0 5 25 30 40
请结合表中信息解答下列问题:
①估计该校1200名学生竞赛成绩的中位数落在哪个分数段内;
②估计该校1200名学生中达到“优秀”的学生总人数.
20.讲禁毒,知今古,教训深,应紧记!某校积极组织开展全国青少年禁毒知识竞赛活动,为了解全校学生的活动情况,随机抽取了50名学生的竞赛成绩,将抽取得到的成绩分为5组,整理后得到下面的频数、频率分布表:
组别 分组 频数/人 频率
1 50≤x<60 3 0.06
2 60≤x<70 a b
3 70≤x<80 14 0.28
4 80≤x<90 6 0.12
5 90≤x<100 20 c
(1)a= ,b= ,c= ;
(2)画出50名学生的竞赛成绩的频数分布直方图.
答案
一、选择题.
A.C.A.A.B.B.
二、填空题
7.8. 8.0.5. 9.0.5. 10.26.
11.3 12.0.4. 13.7. 14.15.
三、解答题
15.解:(1)本次调查的样本容量是:9÷30%=30.
故答案为30;
(2)×30=9(天),
C类:9﹣3=6(天),
B类:6×2=12(天),
补全条形统计图如图所示,
(3)360°×=72°,
即C类在扇形统计图中所对应的圆心角度数是72°;
(4)365×≈256(天).
即本地全年空气质量达到优良以上的约有256天.
16.解:(1)根据题意得:a=1﹣(35%+25%+25%+10%)=5%;
故答案为:5%;
(2)根据题意得:(6+19+17+10+8)×35%=21(人),
则抽取的样本中,八年级学生睡眠时间在C组的有21人;
(3)根据题意得:755×+785×(25%+35%)=453+471=924(人),
答:该校七、八年级学生中睡眠时间合格的共有924人.
17.解:(1)a=5÷=50,
b=50﹣(19+5+4+2)=20;
故答案为50、20;
(2)A等级的频率是=0.38(或38%);
故答案为38%;
(3)B等级所对应的圆心角是×360°=144°.
故答案为144.
18.解:(1)被调查的总人数为5÷0.1=50人;
(2)m=10÷50=0.2、n=50×0.2=10;
(3)估计全校学生中利用手机购物或玩游戏的共有800×(0.1+0.4)=400人.
19.解:(1)根据抽样的代表性、普遍性和可操作性可得,方案三:从三个年级全体学生中随机抽取部分学生成绩进行调查分析,是最符合题意的.
故答案为:方案三;
(2)①样本100人中,成绩从小到大排列后,处在中间位置的两个数都在90≤x<95,因此中位数在90≤x<95组中;
②由题意得,1200×70%=840(人),
答:该校1200名学生中达到“优秀”的有840人.
20.解(1)3÷0.06=50(人),
a=50﹣3﹣14﹣6﹣20=7,
b=7÷50=0.14,
c=20÷50=0.4,
故答案为7,0.14,0.4;
(2)频数分布直方图:
一、选择题.
1.下列六个数:0、、、π、﹣、中,无理数出现的频数是( )
A.3 B.4 C.5 D.6
2.将50个数据分成5组列出频数分布表,其中第一组的频数为6,第二组与第五组的频数和为20,第三组的频率为0.2,则第四组的频率为( )
A.4 B.14 C.0.28 D.50
3.如图是某组15名学生数学测试成绩的频数分布直方图,则成绩低于60分的人数是( )
A.3人 B.6人 C.10人 D.14人
4.下列说法错误的是( )
A.随着试验次数的增多,某一事件发生的频率就会不断增大
B.一个事件A试验中出现的次数越多,频数就越大
C.试验的总次数一定时,频率与频数成正比
D.频数与频率都能反映一个事件出现的频繁程度
5.小文同学统计了他所在小区部分居民每天微信阅读的时间,绘制了直方图.得出了如下结论:①样本中每天阅读微信的时间没人超过1小时,由此可以断定这个小区的居民每天阅读微信时间超过1小时的很少;②样本中每天微信阅读不足20分钟的人数大约占16%;③选取样本的样本容量是60;④估计所有居民每天微信阅读35分钟以上的人数大约占总居民数的一半左右.其中正确的是( )
A.①②③ B.①②④ C.①③④ D.②③④
6.如图为某一试验结果的频率随机试验次数变化趋势图,则下列试验中不符合该图的是( )
A.掷一枚普通正六面体骰子,出现点数不超过2
B.掷一枚硬币,出现正面朝上
C.从装有2个黑球、1个白球的不透明布袋中随机摸出一球为白球
D.从分别标有数字1,2,3,4,5,6,7,8,9的九张卡片中,随机抽取一张卡片所标记的数字不小于7
二、填空题
7.一个容量为100的样本的最大值是120,最小值是48,取组距为10,则可分成 组.
已知算式:﹣(﹣2),﹣|﹣2|,﹣22,(﹣2)×(﹣3),其中负数出现的频率为 .
9.空气质量检测标准规定:当空气质量指数W≤50时,空气质量为优;当50<W≤100时,空气质量为良,当100<Q≤150时,空气质量为轻微污染.已知某城市4月份30天的空气质量状况,统计如表:
空气质量指数(W) 40 60 90 110 120 140
天数 3 5 10 7 4 1
这个月中,空气质量为良的天数的频率为 .
10.某班学生参加学校组织的“垃圾分类”知识竞赛,将学生成绩制成如图所示的频数分布直方图(每组数据包括左端值不包括右端值),其中成绩为“优良”(80分及80分以上)的学生有 人.
11.从谢家集到田家庵有3路,121路,26路三条不同的公交线路.为了解早高峰期间这三条线路上的公交车从谢家集到田家庵的用时时间,在每条线路上随机选取了450个班次的公交车,收集了这些班次的公交车用时(单位:分钟)的数据,统计如下:
线路/用时的频数/用时 40≤t≤45 45<t≤50 50<t≤55 合计
3路 260 167 23 450
121路 160 166 124 450
26路 50 122 278 450
早高峰期间,乘坐 (填“3路”,“121路”或“26路”)线路上的公交车,从谢家集到田家庵“用时不超过50分钟”的可能性最大.
12.数学老师布置10道选择题作为课堂练习,学习委员将全班同学的答题情况绘制成条形图,根据统计图可知,答对8道题的同学的频率是 .
13.某超市为了测定某个时间段收银台开放方案,统计了这个时间段本超市顾客在收银台排队付款的等待时间,并绘制成如下的频数分布直方图(图中等待时间2分钟到3分钟表示大于或等于2分钟而小于3分钟,其它类同).这个时间段内顾客等待时间不少于6分钟的人数为 .
14.某中学开展“阳光体育活动”,九年级一班全体同学在2019年4月18日16时分别参加了巴山舞、乒乓球、篮球三个项目的活动,王老师在此时统计了该班正在参加这三项活动的人数,并绘制了如图所示的频数分布直方图和扇形统计图,根据这两个统计图,可以知道此时该班正在参加乒乓球的人数是 人.
三、解答题
15.小王抽样调查了本地若干天的空气质量情况把空气质量分成四类:A类,B类C类和D类,分别对应的质量级别为优、良、轻度污染和中度污染四种情况,并绘制两个统计图(部分信息缺失):
(1)本次调查的样本容量是 ;
(2)已知C类和D类在扇形统计图中所占的夹角为108度,B类的频数是C类的2倍.通过计算,求出B类和C类的频数,并完成条形统计图;
(3)计算C类在扇形统计图中所对应的圆心角度数;
(4)若一年按365天计算,求本地全年空气质量达到优良以上的天数(保留整数).
16.为了解某校七、八年级学生的睡眠情况,随机抽取了该校七,八年级部分学生进行调査,已知抽取七午级与八年级的学生人数相同,利用抽样所得的数据绘制如下统计图表:
组别 睡眠时间
A x<7.5
B 7.5≤x<8.5
C 8.5≤x<9.5
D 9.5≤x<10.5
E x≥10.5
根据图表提供的信息,回答下列问题:
(1)扇形统计图中的a= ;
(2)抽取的样本中,八年级学生睡眠时间在C组的有多少人?
(3)已知该校七年级学生有755人,八年级学生有785人,如果睡眠吋间x(时)满足7.5≤x<8.5,称睡眠时间合格,试估计该校七、八年级学生中睡眠时间合格的共有多少人?
17.有一学校为了解九年级学生某次体育测试成绩,现对这次体育测试成绩进行随机抽样调查,结果统计如下,其中扇形统计图中C等级所在扇形的圆心角为36°.
被抽取的体育测试成绩频数分布表
等级 成绩(分) 频数(人数)
A 36<x≤40 19
B 32<x≤36 b
C 28<x≤32 5
D 24<x≤28 4
E 20<x≤24 2
合计 a
请你根据以上图表提供的信息,解答下列问题:
(1)a= ,b= ;
(2)A等级的频率是 ;
(3)在扇形统计图中,B等级所对应的圆心角是 度.
18.随着移动终端设备的升级换代,手机已经成为我们生活中不可缺少的一部分,为了解中学生在假期使用
手机的情况(选项:A.和同学亲友聊天;B.学习;C.购物;D.游戏;E.其它),端午节后某中学在全校范围内随机抽取了若干名学生进行调查,得到如右表格(部分信息未给出):
根据以上信息解答下列问题:
选项 频数 频率
A 10 M
B N 0.2
C 5 0.1
D P 0.4
E 5 0.1
(1)这次被调查的学生有多少人?
(2)求表中m,n的值;
(3)若该中学有800名学生,估计全校学生中利用手机购物或玩游戏的共有多少人?
19.为增强学生垃圾分类意识,推动垃圾分类进校园.某初中学校组织全校1200名学生参加了“垃圾分类知识竞赛”,为了解学生的答题情况,学校考虑采用简单随机抽样的方法抽取部分学生的成绩进行调查分析.
(1)学校设计了以下三种抽样调查方案:
方案一:从初一、初二、初三年级中指定部分学生成绩作为样本进行调查分析;
方案二:从初一、初二年级中随机抽取部分男生成绩及在初三年级中随机抽取部分女生成绩进行调查分析;
方案三:从三个年级全体学生中随机抽取部分学生成绩进行调查分析.
其中抽取的样本具有代表性的方案是 .(填“方案一”、“方案二”或“方案三”)
(2)学校根据样本数据,绘制成下表(90分及以上为“优秀”,60分及以上为“及格”):
样本容量 平均分 及格率 优秀率 最高分 最低分
100 93.5 100% 70% 100 80
分数段统计(学生成绩记为x)
分数段 0≤x<80 80≤x<85 85≤x<90 90≤x<95 95≤x≤100
频数 0 5 25 30 40
请结合表中信息解答下列问题:
①估计该校1200名学生竞赛成绩的中位数落在哪个分数段内;
②估计该校1200名学生中达到“优秀”的学生总人数.
20.讲禁毒,知今古,教训深,应紧记!某校积极组织开展全国青少年禁毒知识竞赛活动,为了解全校学生的活动情况,随机抽取了50名学生的竞赛成绩,将抽取得到的成绩分为5组,整理后得到下面的频数、频率分布表:
组别 分组 频数/人 频率
1 50≤x<60 3 0.06
2 60≤x<70 a b
3 70≤x<80 14 0.28
4 80≤x<90 6 0.12
5 90≤x<100 20 c
(1)a= ,b= ,c= ;
(2)画出50名学生的竞赛成绩的频数分布直方图.
答案
一、选择题.
A.C.A.A.B.B.
二、填空题
7.8. 8.0.5. 9.0.5. 10.26.
11.3 12.0.4. 13.7. 14.15.
三、解答题
15.解:(1)本次调查的样本容量是:9÷30%=30.
故答案为30;
(2)×30=9(天),
C类:9﹣3=6(天),
B类:6×2=12(天),
补全条形统计图如图所示,
(3)360°×=72°,
即C类在扇形统计图中所对应的圆心角度数是72°;
(4)365×≈256(天).
即本地全年空气质量达到优良以上的约有256天.
16.解:(1)根据题意得:a=1﹣(35%+25%+25%+10%)=5%;
故答案为:5%;
(2)根据题意得:(6+19+17+10+8)×35%=21(人),
则抽取的样本中,八年级学生睡眠时间在C组的有21人;
(3)根据题意得:755×+785×(25%+35%)=453+471=924(人),
答:该校七、八年级学生中睡眠时间合格的共有924人.
17.解:(1)a=5÷=50,
b=50﹣(19+5+4+2)=20;
故答案为50、20;
(2)A等级的频率是=0.38(或38%);
故答案为38%;
(3)B等级所对应的圆心角是×360°=144°.
故答案为144.
18.解:(1)被调查的总人数为5÷0.1=50人;
(2)m=10÷50=0.2、n=50×0.2=10;
(3)估计全校学生中利用手机购物或玩游戏的共有800×(0.1+0.4)=400人.
19.解:(1)根据抽样的代表性、普遍性和可操作性可得,方案三:从三个年级全体学生中随机抽取部分学生成绩进行调查分析,是最符合题意的.
故答案为:方案三;
(2)①样本100人中,成绩从小到大排列后,处在中间位置的两个数都在90≤x<95,因此中位数在90≤x<95组中;
②由题意得,1200×70%=840(人),
答:该校1200名学生中达到“优秀”的有840人.
20.解(1)3÷0.06=50(人),
a=50﹣3﹣14﹣6﹣20=7,
b=7÷50=0.14,
c=20÷50=0.4,
故答案为7,0.14,0.4;
(2)频数分布直方图:
