沪科版八年级数学下册 20.2 数据的集中趋势与离散程度 试题(含答案)
文档属性
| 名称 | 沪科版八年级数学下册 20.2 数据的集中趋势与离散程度 试题(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 150.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-07 10:26:23 | ||
图片预览




文档简介
20.2 数据的集中趋势与离散程度
一、选择题.
1.某校射击队从甲、乙、丙、丁四人中选拔一人参加市运会射击比赛.在选拔赛中,每人射击10次,他们10次成绩的平均数及方差如下表所示:
甲 乙 丙 丁
平均数/环 9.7 9.5 9.5 9.7
方差/环2 5.1 4.7 4.5 4.5
请你根据表中数据选一人参加比赛,最合适的人选是( )
A.甲 B.乙 C.丙 D.丁
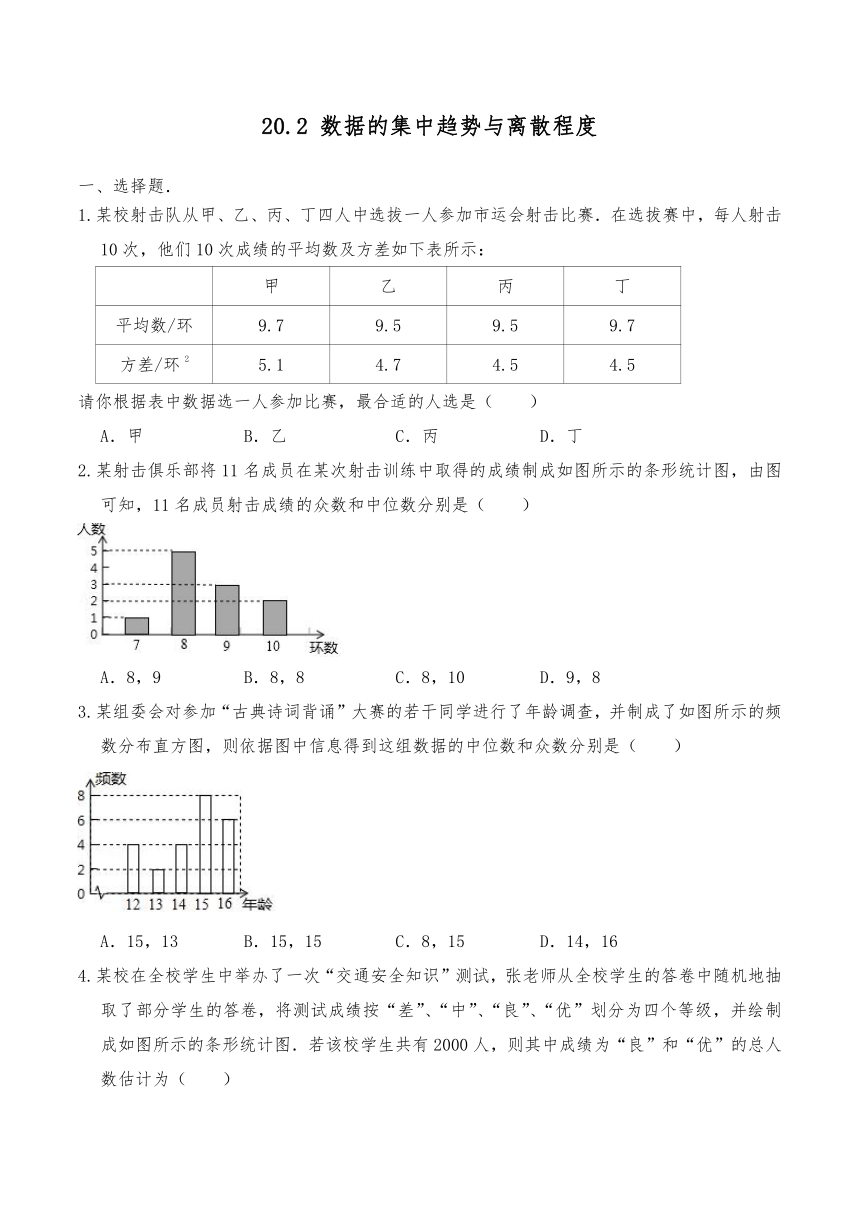
2.某射击俱乐部将11名成员在某次射击训练中取得的成绩制成如图所示的条形统计图,由图可知,11名成员射击成绩的众数和中位数分别是( )
A.8,9 B.8,8 C.8,10 D.9,8
3.某组委会对参加“古典诗词背诵”大赛的若干同学进行了年龄调查,并制成了如图所示的频数分布直方图,则依据图中信息得到这组数据的中位数和众数分别是( )
A.15,13 B.15,15 C.8,15 D.14,16
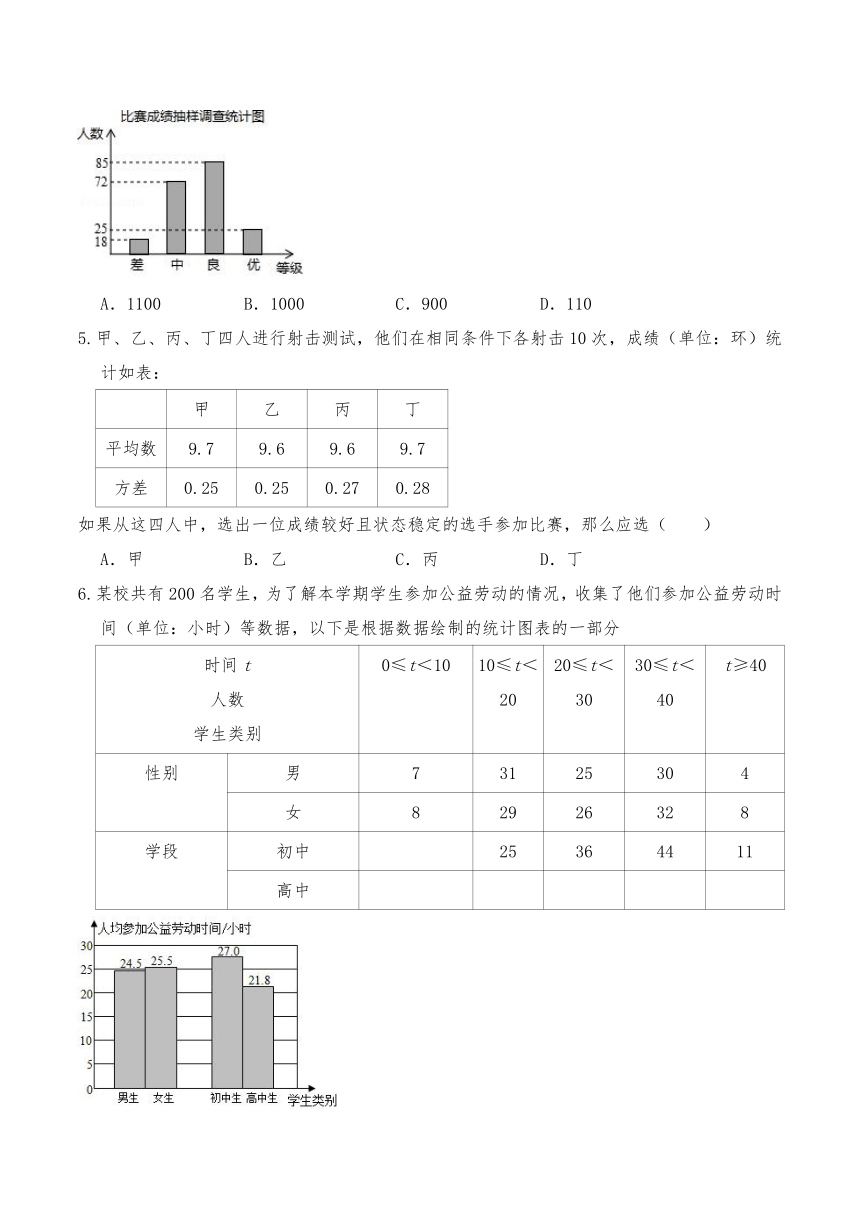
4.某校在全校学生中举办了一次“交通安全知识”测试,张老师从全校学生的答卷中随机地抽取了部分学生的答卷,将测试成绩按“差”、“中”、“良”、“优”划分为四个等级,并绘制成如图所示的条形统计图.若该校学生共有2000人,则其中成绩为“良”和“优”的总人数估计为( )
A.1100 B.1000 C.900 D.110
5.甲、乙、丙、丁四人进行射击测试,他们在相同条件下各射击10次,成绩(单位:环)统计如表:
甲 乙 丙 丁
平均数 9.7 9.6 9.6 9.7
方差 0.25 0.25 0.27 0.28
如果从这四人中,选出一位成绩较好且状态稳定的选手参加比赛,那么应选( )
A.甲 B.乙 C.丙 D.丁
6.某校共有200名学生,为了解本学期学生参加公益劳动的情况,收集了他们参加公益劳动时间(单位:小时)等数据,以下是根据数据绘制的统计图表的一部分
时间t 人数 学生类别 0≤t<10 10≤t<20 20≤t<30 30≤t<40 t≥40
性别 男 7 31 25 30 4
女 8 29 26 32 8
学段 初中 25 36 44 11
高中
下面有四个推断:
①这200名学生参加公益劳动时间的平均数一定在24.5h~25.5h之间;
②这200名学生参加公益劳动时间的中位数在20h~30h之间;
③这200名学生中的高中生参加公益劳动时间的中位数可能在20h~30h之间;
④这200名学生中的初中生参加公益劳动时间的中位数一定在20h~30h之间.
所有合理推断的序号是( )
A.①②③④ B.①②④ C.①②③ D.①④
二、填空题
7.数据6,5,x,4,7的平均数是5,那么这组数据的方差为 .
8.某区10名学生参加实际汉字听写大赛,他们得分情况如表:那么10名学生所得分数的中位数是 .
人数 3 4 2 1
分数 80 85 90 95
9.某校即将举行30周年校庆,拟定了A,B,C,D四种活动方案,为了解学生对方案的意见,学校随机抽取了部分学生进行问卷调查(每人只能赞成一种方案),将调查结果进行统计并绘制成如图两幅不完整的统计图.若该校有学生3000人,请根据以上统计结果估计该校学生赞成方案B的人数为 .
甲、乙两支球队队员的平均身高相等,且两支球队队员的身高方差分别为s=0.18,s=0.32,则身高较整齐的球队是 队.(填“甲”或“乙”)
11.在一场比赛中,甲、乙两名射击手的5次射击成绩统计如图所示,分别记甲、乙两人这场比赛成绩的方差为S甲2,S乙2,则S甲2 S乙2(填“>”或“<”).
12.为了保护环境,环保部门每天都要对重点城市的空气污染情况进行监控和预报,当污染指数w≤50时,空气质量为优;当污染指数50<w≤100时,空气质量为良;当污染指数100<w≤150时,空气质量为轻度污染……现随机抽取某城市30天的空气质量情况统计如表:
污染指数(w) 40 70 90 110 120 140
天数(t) 3 8 9 6 3 1
估计这个城市一年(365天)中,空气质量达到良以上的天数是 .
13.某中学数学兴趣小组在一次课外学习与探究中遇到一些新的数学符号,他们将其中某些材料摘录如下:
对于三个实数a,b,c,用M{a,b,c}表示这三个数的平均数,用min{a,b,c}表示这三个数中最小的数.例如:M{1,2,9}==4,min{1,2,﹣3}=﹣3,min{3,1,1}=1.
请结合上述材料,解决下列问题:
(1)M{(﹣2)2,22,﹣22}= ;
(2)若min{3﹣2x,1+3x,﹣5}=﹣5,则x的取值范围为 .
14.已知数据a1,a2,a3,a4,a5的平均数是m,且a1>a2>a3>a4>a5>0,则数据a1,a2,a3,﹣3,a4,a5的平均数和中位数分别是 , .
三、解答题
15.为了从甲、乙两名选手中选拔一个参加射击比赛,现对他们进行一次测试,两个人在相同条件下各射靶5次,甲命中的环数分别是:10、6、10、6、8,乙命中的环数分别是:7、9、7、8、9.经过计算,甲命中的平均数为=8,方差为S甲2=3.2.
(1)求乙命中的平均数和方差S乙2:
(2)现从甲、乙两名队员中选出一人去参加射击比赛,你认为应该选哪名队员去?为什么?
16.扬州教育推出的“智慧学堂”已成为同学们课外学习的得力助手.为了解同学们“智慧学堂”平台使用的熟练程度,某校随机抽取了部分同学进行调查,并将调查结果绘制成如图两幅尚不完整的统计图.
根据以上信息,回答下列问题:
(1)本次调查的样本容量是 ,扇形统计图中表示A等级的扇形圆心角为 °;
(2)补全条形统计图;
(3)学校拟对“不太熟练或不熟练”的同学进行平台使用的培训,若该校有2000名学生,试估计该校需要培训的学生人数.
17.某次数学测验中,一道题满分3分,老师评分只给整数,即得分只能为0分,1分,2分,3分.李老师为了了解学生得分情况和试题的难易情况,对初三(1)班所有学生的试题进行了分析整理,并绘制了两幅尚不完整的统计图,如图所示.
小知识
难度系数的计算公式为:L=,其中L为难度系数,X为样本平均数,W为试题满分值.
《考试说明》指出:L在0.7以上的题为容易题;在0.4﹣0.7之间的题为中档题;L在0.2﹣0.4之间的题为较难题.
解答下列问题:
(1)m= ,n= ,并补全条形统计图;
(2)在初三(1)班随机抽取一名学生的成绩,求抽中的成绩为得分众数的概率;
(3)根据右侧“小知识”,通过计算判断这道题对于该班级来说,属于哪一类难度的试题?
18.为了解某区初二年级数学学科期末质量监控情况,进行了抽样调查,过程如下:
收集数据:随机抽取甲乙两所学校的各20名学生的数学成绩进行分析:
甲 91 89 77 86 71 31 97 93 72 91 81 92 85 85 95 88 88 90 44 91
乙 84 93 66 69 76 87 77 82 85 88 90 88 67 88 91 96 68 97 59 88
整理、描述数据:按如下数据段整理、描述这两组数据
分段 30≤x≤39 40≤x≤49 50≤x≤59 60≤x≤69 70≤x≤79 80≤x≤89 90≤x≤99
甲 1 1 0 0 3 7 8
乙
分析数据:两组数据的平均数、中位数、众数、方差如表:
统计量 平均数 中位数 众数 方差
甲 81.85 88 91 268.43
乙 81.95 m 88 115.25
经统计,表格中m的值是 .
得出结论:
a若甲学校有500名初二学生,估计这次考试成绩80分以下的人数为 .
b可以推断出 学校初二学生的数学水平较高,理由为: .(至少从两个不同的角度说明推断的合理性)
19.某汽车经销商为了能更好的了解某季度纯电动汽车的续航能力,现分两次不重复的各抽取了10台纯电动车进行了续航里程的测试.并将测试的情况进行整理、描述和分析(续航里程用x表示,共分成四组:(A)100≤x<200,(B)200≤x<300,(C)300≤x<400,(D)x≥400,单位:km).下面给出了部分信息:
第一次抽取10台车的续航里程在C组中的数据是:380,310,300,310.
第二次抽取10台车的续航里程是:220,301,175,310,400,310,385,430,234,455.
第一次测试的续航里程扇形统计图如图
两次测试的续航里程统计表
第一次 第二次
平均里程 321.4 b
中位数 c 310
众数 310 310
根据以上信息,解答下列问题:
(1)直接写出上述图表中a、b、c的值,a= ,b= ,c .
(2)根据以上数据,你认为这两次测试中的哪一次的纯电动汽车续航能力更强?请说明理由(一条理由即可).
(3)若经销商这一季度共购进1600台纯电动汽车,结合这两次测试,估计这一季度续航能力较强(x≥380)的纯电动汽车有多少辆?
20.某校为了提升初中学生学习数学的兴趣,培养学生的创新精神,举办“玩转数学”比赛,评选出冠军组.现有甲、乙、丙三个小组进入决赛,评委从研究报告、小组展示、答辩三个方面进行量化考核,各项得分如表:
小组 研究报告(分) 小组展示(分) 答辩(分)
甲 83 79 90
乙 82 88 79
丙 88 83 75
(1)根据三项得分的平均分,从高到低确定三名应聘者的排名顺序.
(2)该校规定:研究报告、小组展示、答辩分分别不得低于80分,80分,70分,并按50%,30%,20%的比例计入总分.根据规定,请你通过计算说明哪一组获得冠军.
答案
一、选择题.
D.B.B.A.A.B.
二、填空题
7.2. 8.85分. 9.1800人. 10.甲.
11.<. 12.243天.
13.(1)(2)﹣2≤x≤4. 14.算术平均数、中位数
三、解答题
15.解:(1)乙命中的平均数=(7+9+7+8+9)÷5=8,
方差S乙2=[(7﹣8)2+(9﹣8)2+(7﹣8)2+(8﹣8)2+(9﹣8)2]=0.8;
(2)选乙队员去.因为甲、乙两名选手命中的平均数相同,但是S甲2>S乙2,所以乙的成绩较稳定(答案不唯一,有理由即可).
16.解:(1)本次调查的样本容量是150÷30%=500,
扇形统计图中表示A等级的扇形圆心角为:360°×30%=108°,
故答案为:500,108;
(2)B等级的人数为:500×40%=200,
补全的条形统计图如右图所示;
(3)2000×=200(人),
答:该校需要培训的学生有200人.
17.解:(1)解:(1)由条形统计图可知0分的同学有6人,由扇形统计图可知,0分的同学占10%,
∴抽取的总人数是:6÷10%=60(人),
故得1分的学生数是;60﹣27﹣12﹣6=15(人),
∴m%=×100%,
解得:m=25,
n%=×100%=20%,
故答案为:25,20;
(2)总人数为60人,众数为(2分)有27人,概率为=或者(0.45);
(3)平均数为:=1.75(分),
L==≈0.58,
因为0.58在0.4﹣0.7中间,所以这道题为中档题.
18.解: 0 0 1 4 2 8 5
将乙学校的成绩从小到大排列后处在中间位置的两个数的平均数为=86,因此中位数是86,即m=86,
故答案为:86;
500×=125(人),
故答案为:125;
故答案为:甲,甲学校虽然平均分稍低一点,但甲学校的中位数、众数均比乙学校的高.
19.解:(1)a%=1﹣×100%﹣30%﹣10%=20%,
∴a=20;
b=(220+301+175+310+400+310+385+430+234+455)=322;
c==305;
(2)第2次的纯电动汽车续航能力更强,理由:第二次的平均数大于第一次的平均数;
(3)1600×=560(辆),
答:估计这一季度续航能力较强(x≥380)的纯电动汽车有560辆.
20.解:(1)==84(分),
==83(分),
==82(分),
∵84>83>82,
∴根据三项得分的平均分,从高到低确定三名应聘者的排名顺序是甲、乙、丙;
(2)由题意可知,只有甲不符合规定,
乙的成绩为:82×50%+88×30%+79×20%=83.2(分),
丙的成绩为:88×50%+83×30%+75×20%=83.9(分),
∵83.9>83.2,
∴丙组获得冠军.
一、选择题.
1.某校射击队从甲、乙、丙、丁四人中选拔一人参加市运会射击比赛.在选拔赛中,每人射击10次,他们10次成绩的平均数及方差如下表所示:
甲 乙 丙 丁
平均数/环 9.7 9.5 9.5 9.7
方差/环2 5.1 4.7 4.5 4.5
请你根据表中数据选一人参加比赛,最合适的人选是( )
A.甲 B.乙 C.丙 D.丁
2.某射击俱乐部将11名成员在某次射击训练中取得的成绩制成如图所示的条形统计图,由图可知,11名成员射击成绩的众数和中位数分别是( )
A.8,9 B.8,8 C.8,10 D.9,8
3.某组委会对参加“古典诗词背诵”大赛的若干同学进行了年龄调查,并制成了如图所示的频数分布直方图,则依据图中信息得到这组数据的中位数和众数分别是( )
A.15,13 B.15,15 C.8,15 D.14,16
4.某校在全校学生中举办了一次“交通安全知识”测试,张老师从全校学生的答卷中随机地抽取了部分学生的答卷,将测试成绩按“差”、“中”、“良”、“优”划分为四个等级,并绘制成如图所示的条形统计图.若该校学生共有2000人,则其中成绩为“良”和“优”的总人数估计为( )
A.1100 B.1000 C.900 D.110
5.甲、乙、丙、丁四人进行射击测试,他们在相同条件下各射击10次,成绩(单位:环)统计如表:
甲 乙 丙 丁
平均数 9.7 9.6 9.6 9.7
方差 0.25 0.25 0.27 0.28
如果从这四人中,选出一位成绩较好且状态稳定的选手参加比赛,那么应选( )
A.甲 B.乙 C.丙 D.丁
6.某校共有200名学生,为了解本学期学生参加公益劳动的情况,收集了他们参加公益劳动时间(单位:小时)等数据,以下是根据数据绘制的统计图表的一部分
时间t 人数 学生类别 0≤t<10 10≤t<20 20≤t<30 30≤t<40 t≥40
性别 男 7 31 25 30 4
女 8 29 26 32 8
学段 初中 25 36 44 11
高中
下面有四个推断:
①这200名学生参加公益劳动时间的平均数一定在24.5h~25.5h之间;
②这200名学生参加公益劳动时间的中位数在20h~30h之间;
③这200名学生中的高中生参加公益劳动时间的中位数可能在20h~30h之间;
④这200名学生中的初中生参加公益劳动时间的中位数一定在20h~30h之间.
所有合理推断的序号是( )
A.①②③④ B.①②④ C.①②③ D.①④
二、填空题
7.数据6,5,x,4,7的平均数是5,那么这组数据的方差为 .
8.某区10名学生参加实际汉字听写大赛,他们得分情况如表:那么10名学生所得分数的中位数是 .
人数 3 4 2 1
分数 80 85 90 95
9.某校即将举行30周年校庆,拟定了A,B,C,D四种活动方案,为了解学生对方案的意见,学校随机抽取了部分学生进行问卷调查(每人只能赞成一种方案),将调查结果进行统计并绘制成如图两幅不完整的统计图.若该校有学生3000人,请根据以上统计结果估计该校学生赞成方案B的人数为 .
甲、乙两支球队队员的平均身高相等,且两支球队队员的身高方差分别为s=0.18,s=0.32,则身高较整齐的球队是 队.(填“甲”或“乙”)
11.在一场比赛中,甲、乙两名射击手的5次射击成绩统计如图所示,分别记甲、乙两人这场比赛成绩的方差为S甲2,S乙2,则S甲2 S乙2(填“>”或“<”).
12.为了保护环境,环保部门每天都要对重点城市的空气污染情况进行监控和预报,当污染指数w≤50时,空气质量为优;当污染指数50<w≤100时,空气质量为良;当污染指数100<w≤150时,空气质量为轻度污染……现随机抽取某城市30天的空气质量情况统计如表:
污染指数(w) 40 70 90 110 120 140
天数(t) 3 8 9 6 3 1
估计这个城市一年(365天)中,空气质量达到良以上的天数是 .
13.某中学数学兴趣小组在一次课外学习与探究中遇到一些新的数学符号,他们将其中某些材料摘录如下:
对于三个实数a,b,c,用M{a,b,c}表示这三个数的平均数,用min{a,b,c}表示这三个数中最小的数.例如:M{1,2,9}==4,min{1,2,﹣3}=﹣3,min{3,1,1}=1.
请结合上述材料,解决下列问题:
(1)M{(﹣2)2,22,﹣22}= ;
(2)若min{3﹣2x,1+3x,﹣5}=﹣5,则x的取值范围为 .
14.已知数据a1,a2,a3,a4,a5的平均数是m,且a1>a2>a3>a4>a5>0,则数据a1,a2,a3,﹣3,a4,a5的平均数和中位数分别是 , .
三、解答题
15.为了从甲、乙两名选手中选拔一个参加射击比赛,现对他们进行一次测试,两个人在相同条件下各射靶5次,甲命中的环数分别是:10、6、10、6、8,乙命中的环数分别是:7、9、7、8、9.经过计算,甲命中的平均数为=8,方差为S甲2=3.2.
(1)求乙命中的平均数和方差S乙2:
(2)现从甲、乙两名队员中选出一人去参加射击比赛,你认为应该选哪名队员去?为什么?
16.扬州教育推出的“智慧学堂”已成为同学们课外学习的得力助手.为了解同学们“智慧学堂”平台使用的熟练程度,某校随机抽取了部分同学进行调查,并将调查结果绘制成如图两幅尚不完整的统计图.
根据以上信息,回答下列问题:
(1)本次调查的样本容量是 ,扇形统计图中表示A等级的扇形圆心角为 °;
(2)补全条形统计图;
(3)学校拟对“不太熟练或不熟练”的同学进行平台使用的培训,若该校有2000名学生,试估计该校需要培训的学生人数.
17.某次数学测验中,一道题满分3分,老师评分只给整数,即得分只能为0分,1分,2分,3分.李老师为了了解学生得分情况和试题的难易情况,对初三(1)班所有学生的试题进行了分析整理,并绘制了两幅尚不完整的统计图,如图所示.
小知识
难度系数的计算公式为:L=,其中L为难度系数,X为样本平均数,W为试题满分值.
《考试说明》指出:L在0.7以上的题为容易题;在0.4﹣0.7之间的题为中档题;L在0.2﹣0.4之间的题为较难题.
解答下列问题:
(1)m= ,n= ,并补全条形统计图;
(2)在初三(1)班随机抽取一名学生的成绩,求抽中的成绩为得分众数的概率;
(3)根据右侧“小知识”,通过计算判断这道题对于该班级来说,属于哪一类难度的试题?
18.为了解某区初二年级数学学科期末质量监控情况,进行了抽样调查,过程如下:
收集数据:随机抽取甲乙两所学校的各20名学生的数学成绩进行分析:
甲 91 89 77 86 71 31 97 93 72 91 81 92 85 85 95 88 88 90 44 91
乙 84 93 66 69 76 87 77 82 85 88 90 88 67 88 91 96 68 97 59 88
整理、描述数据:按如下数据段整理、描述这两组数据
分段 30≤x≤39 40≤x≤49 50≤x≤59 60≤x≤69 70≤x≤79 80≤x≤89 90≤x≤99
甲 1 1 0 0 3 7 8
乙
分析数据:两组数据的平均数、中位数、众数、方差如表:
统计量 平均数 中位数 众数 方差
甲 81.85 88 91 268.43
乙 81.95 m 88 115.25
经统计,表格中m的值是 .
得出结论:
a若甲学校有500名初二学生,估计这次考试成绩80分以下的人数为 .
b可以推断出 学校初二学生的数学水平较高,理由为: .(至少从两个不同的角度说明推断的合理性)
19.某汽车经销商为了能更好的了解某季度纯电动汽车的续航能力,现分两次不重复的各抽取了10台纯电动车进行了续航里程的测试.并将测试的情况进行整理、描述和分析(续航里程用x表示,共分成四组:(A)100≤x<200,(B)200≤x<300,(C)300≤x<400,(D)x≥400,单位:km).下面给出了部分信息:
第一次抽取10台车的续航里程在C组中的数据是:380,310,300,310.
第二次抽取10台车的续航里程是:220,301,175,310,400,310,385,430,234,455.
第一次测试的续航里程扇形统计图如图
两次测试的续航里程统计表
第一次 第二次
平均里程 321.4 b
中位数 c 310
众数 310 310
根据以上信息,解答下列问题:
(1)直接写出上述图表中a、b、c的值,a= ,b= ,c .
(2)根据以上数据,你认为这两次测试中的哪一次的纯电动汽车续航能力更强?请说明理由(一条理由即可).
(3)若经销商这一季度共购进1600台纯电动汽车,结合这两次测试,估计这一季度续航能力较强(x≥380)的纯电动汽车有多少辆?
20.某校为了提升初中学生学习数学的兴趣,培养学生的创新精神,举办“玩转数学”比赛,评选出冠军组.现有甲、乙、丙三个小组进入决赛,评委从研究报告、小组展示、答辩三个方面进行量化考核,各项得分如表:
小组 研究报告(分) 小组展示(分) 答辩(分)
甲 83 79 90
乙 82 88 79
丙 88 83 75
(1)根据三项得分的平均分,从高到低确定三名应聘者的排名顺序.
(2)该校规定:研究报告、小组展示、答辩分分别不得低于80分,80分,70分,并按50%,30%,20%的比例计入总分.根据规定,请你通过计算说明哪一组获得冠军.
答案
一、选择题.
D.B.B.A.A.B.
二、填空题
7.2. 8.85分. 9.1800人. 10.甲.
11.<. 12.243天.
13.(1)(2)﹣2≤x≤4. 14.算术平均数、中位数
三、解答题
15.解:(1)乙命中的平均数=(7+9+7+8+9)÷5=8,
方差S乙2=[(7﹣8)2+(9﹣8)2+(7﹣8)2+(8﹣8)2+(9﹣8)2]=0.8;
(2)选乙队员去.因为甲、乙两名选手命中的平均数相同,但是S甲2>S乙2,所以乙的成绩较稳定(答案不唯一,有理由即可).
16.解:(1)本次调查的样本容量是150÷30%=500,
扇形统计图中表示A等级的扇形圆心角为:360°×30%=108°,
故答案为:500,108;
(2)B等级的人数为:500×40%=200,
补全的条形统计图如右图所示;
(3)2000×=200(人),
答:该校需要培训的学生有200人.
17.解:(1)解:(1)由条形统计图可知0分的同学有6人,由扇形统计图可知,0分的同学占10%,
∴抽取的总人数是:6÷10%=60(人),
故得1分的学生数是;60﹣27﹣12﹣6=15(人),
∴m%=×100%,
解得:m=25,
n%=×100%=20%,
故答案为:25,20;
(2)总人数为60人,众数为(2分)有27人,概率为=或者(0.45);
(3)平均数为:=1.75(分),
L==≈0.58,
因为0.58在0.4﹣0.7中间,所以这道题为中档题.
18.解: 0 0 1 4 2 8 5
将乙学校的成绩从小到大排列后处在中间位置的两个数的平均数为=86,因此中位数是86,即m=86,
故答案为:86;
500×=125(人),
故答案为:125;
故答案为:甲,甲学校虽然平均分稍低一点,但甲学校的中位数、众数均比乙学校的高.
19.解:(1)a%=1﹣×100%﹣30%﹣10%=20%,
∴a=20;
b=(220+301+175+310+400+310+385+430+234+455)=322;
c==305;
(2)第2次的纯电动汽车续航能力更强,理由:第二次的平均数大于第一次的平均数;
(3)1600×=560(辆),
答:估计这一季度续航能力较强(x≥380)的纯电动汽车有560辆.
20.解:(1)==84(分),
==83(分),
==82(分),
∵84>83>82,
∴根据三项得分的平均分,从高到低确定三名应聘者的排名顺序是甲、乙、丙;
(2)由题意可知,只有甲不符合规定,
乙的成绩为:82×50%+88×30%+79×20%=83.2(分),
丙的成绩为:88×50%+83×30%+75×20%=83.9(分),
∵83.9>83.2,
∴丙组获得冠军.
