沪科版八年级数学下册试题19.4综合与实践 多边形的镶嵌(含答案)
文档属性
| 名称 | 沪科版八年级数学下册试题19.4综合与实践 多边形的镶嵌(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 147.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-07 00:00:00 | ||
图片预览



文档简介
19.4综合与实践 多边形的镶嵌
一、选择题
1.用一些形状大小完全相同的图形不能镶嵌成平面图案的是( )
A.三角形 B.菱形 C.正六边形 D.正七边形
2.利用边长相等的正三角形和正六边形地砖能够铺满地板,若每个顶点处有a块正三角形和b块正六边形(a>b>0),则a+b的值为( )
A.4 B.5 C.6 D.7
3.下列正多边形的组合中,能够铺满地面的是( )
A.正六边形和正八边形 B.正四边形和正五边形
C.正三边形和正六边形 D.正四边形和正六边形
4.下列正多边形瓷砖中,若仅用种瓷砖铺地面,则不能将地面密铺的是( )
A.正三角形 B.正四边形 C.正五边形 D.正六边形
5.用正三角形和正方形组合能够铺满地面,每个顶点周围有m个正三角形和n个正方形(m、n为正整数),则m+n的值为( )
A.4 B.3 C.6 D.5
6.用形状、大小完全相同的下列图形,不能拼成既无缝隙又不重叠的图形的是( )
A.三角形 B.四边形 C.正五边形 D.正六边形
7.垦区小城镇建设如火如荼,小红家买了新楼.爸爸在正三角形、正方形、正五边形、正六边形四种瓷砖中,只购买一种瓷砖进行平铺,有几种购买方式( )
A.1种 B.2种 C.3种 D.4种
8.小飞家房屋装修时,选中了一种漂亮的正八边形地砖,建材店老板告诉她,只用一种八边形地砖是不能铺满地面的,但可以与另外一种形状的地砖混合使用,你认为要使地面铺满,小飞应选择另一种( )形状的地砖.
A.正三角形 B.正方形 C.正五边形 D.正六边形
9.正多边形通过镶嵌能够密铺成一个无缝隙的平面,下列组合中不能镶嵌成一个平面的是( )
A.正三角形和正方形 B.正三角形和正六边形
C.正方形和正六边形 D.正方形和正八边形
10.如图,某休闲广场是用边长相等的正四边形和正八边形的地砖组合,在每个顶点处无缝隙、无重叠的铺设,而且地砖完整.除此之外,还可以选择无缝隙、无重叠铺设的正多边形组合是( )
A.正三边形、正四边形 B.正四边形、正五边形
C.正五边形、正六边形 D.正六边形、正八边形
填空题
11.用一种正五边形或正八边形的瓷砖 铺满地面(填“能”或“不能”).
12.用正三角形和正六边形镶嵌,在每个顶点处有 个正三角形和 个正六边形,
13.现有①正三角形、②正方形、③正五边形三种形状的地砖,只选取其中一种地砖镶嵌地面,不能进行地面镶嵌的有 (填序号).
14.现有四种地面砖,它们的形状分别是:正三角形、正方形、正六边形、正八边形,且它们的边长都相等.同时选择其中两种地面砖密铺地面,选择的方式可以是 .
A.正三角形和正四边形
B.正三角形与正六边形
C.正方形与正八边形
D.正三角形与正八边形
15.下列正多边形组合中,能够铺满地面的是 .
A.正八边形和正方形
B.正三角形,正方形和正六边形
C.正三角形和正六边形
D.正方形和正六边形
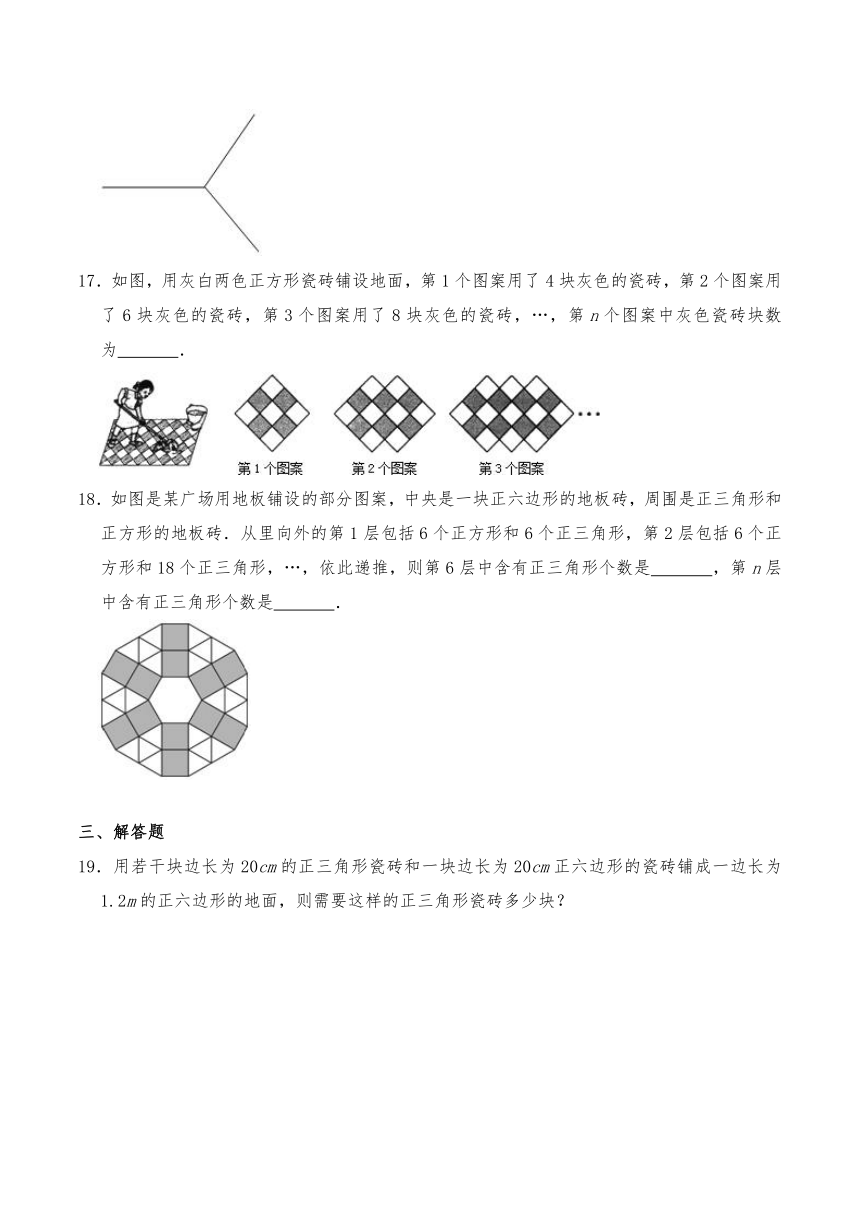
16.如图所示是三个相同的正n边形拼成的无缝隙、不重叠的图形的一部分,则n的值为 .
17.如图,用灰白两色正方形瓷砖铺设地面,第1个图案用了4块灰色的瓷砖,第2个图案用了6块灰色的瓷砖,第3个图案用了8块灰色的瓷砖,…,第n个图案中灰色瓷砖块数为 .
18.如图是某广场用地板铺设的部分图案,中央是一块正六边形的地板砖,周围是正三角形和正方形的地板砖.从里向外的第1层包括6个正方形和6个正三角形,第2层包括6个正方形和18个正三角形,…,依此递推,则第6层中含有正三角形个数是 ,第n层中含有正三角形个数是 .
三、解答题
19.用若干块边长为20cm的正三角形瓷砖和一块边长为20cm正六边形的瓷砖铺成一边长为1.2m的正六边形的地面,则需要这样的正三角形瓷砖多少块?
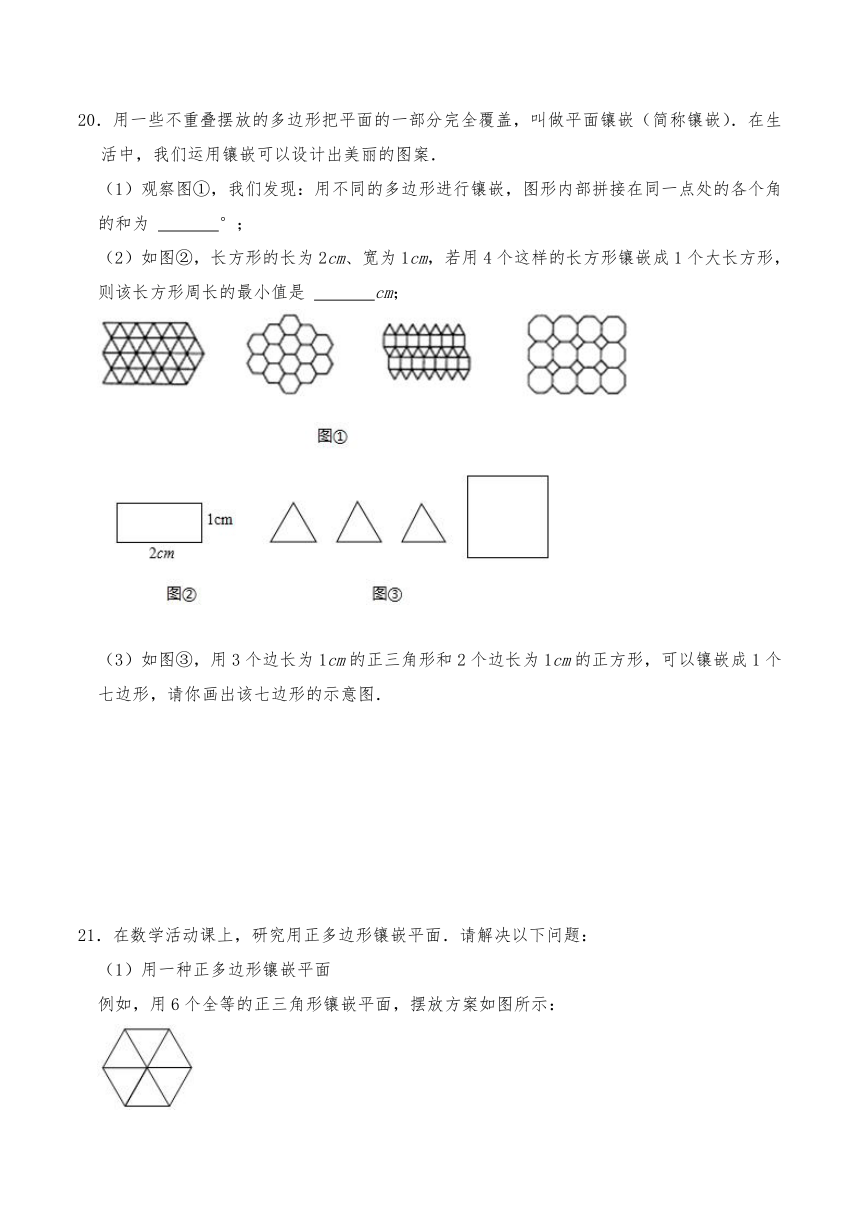
20.用一些不重叠摆放的多边形把平面的一部分完全覆盖,叫做平面镶嵌(简称镶嵌).在生活中,我们运用镶嵌可以设计出美丽的图案.
(1)观察图①,我们发现:用不同的多边形进行镶嵌,图形内部拼接在同一点处的各个角的和为 °;
(2)如图②,长方形的长为2cm、宽为1cm,若用4个这样的长方形镶嵌成1个大长方形,则该长方形周长的最小值是 cm;
(3)如图③,用3个边长为1cm的正三角形和2个边长为1cm的正方形,可以镶嵌成1个七边形,请你画出该七边形的示意图.
21.在数学活动课上,研究用正多边形镶嵌平面.请解决以下问题:
(1)用一种正多边形镶嵌平面
例如,用6个全等的正三角形镶嵌平面,摆放方案如图所示:
若用m个全等的正n边形镶嵌平面,求出m,n应满足的关系式;
(2)用两种正多边形镶嵌平面
若这两种正多边形分别是边长相等的正三角形和正方形,请画出两种不同的摆放方案;
(3)用多种正多边形镶嵌平面
若镶嵌时每个顶点处的正多边形有n个,设这n个正多边形的边数分别为x1,x2,…,xn,求出x1,x2,…,xn应满足的关系式.(用含n的式子表示)
22.我们知道,可以单独用正三角形、正方形或正六边形铺满地面,如果我们要同时用两种不同的正多边形铺满地面,可以设计出几种不同的组合方案?
问题解决:
猜想1:是否可以同时用正方形、正八边形两种正多边形组合铺满地面?
验证1并完成填空:在铺地面时,设围绕某一个点有x个正方形和y个正八边形的内角可以拼成一个周角.根据题意:可得方程①: ,
整理得②: ,
我们可以找到方程的正整数解为③: .
结论1:铺满地面时,在一个顶点周围围绕着④ 个正方形和⑤ 个正八边形的内角可以拼成一个周角,所以同时用正方形和正八边形两种正多边形组合可以铺满地面.
猜想2:是否可以同时用正三角形和正六边形两种正多边形组合铺满地面?若能,请按照上述方法进行验证,并写出所有可能的方案;若不能,请说明理由.
23.数学问题:用边长相等的正三角形、正方形和正六边形能否进行平面图形的镶嵌?
问题探究:为了解决上述数学问题,我们采用分类讨论的思想方法去进行探究.
探究一:从正三角形、正方形和正六边形中任选一种图形,能否进行平面图形的镶嵌?
第一类:选正三角形.因为正三角形的每一个内角是60°,所以在镶嵌平面时,围绕某一点有6个正三角形的内角可以拼成一个周角,所以用正三角形可以进行平面图形的镶嵌.
第二类:选正方形.因为正方形的每一个内角是90°,所以在镶嵌平面时,围绕某一点有4个正方形的内角可以拼成一个周角,所以用正方形也可以进行平面图形的镶嵌.
第三类:选正六边形.(仿照上述方法,写出探究过程及结论)
探究二:从正三角形、正方形和正六边形中任选两种图形,能否进行平面图形的镶嵌?
第四类:选正三角形和正方形
在镶嵌平面时,设围绕某一点有x个正三角形和y个正方形的内角可以拼成个周角.根据题意,可得方程
60x+90y=360
整理,得2x+3y=12.
我们可以找到唯一组适合方程的正整数解为
镶嵌平面时,在一个顶点周围围绕着3个正三角形和2个正方形的内角可以拼成一个周角,所以用正三角形和正方形可以进行平面镶嵌
第五类:选正三角形和正六边形.(仿照上述方法,写出探究过程及结论)
第六类:选正方形和正六边形,(不写探究过程,只写出结论)
探究三:用正三角形、正方形和正六边形三种图形是否可以镶嵌平面?
第七类:选正三角形、正方形和正六边形三种图形.(不写探究过程,只写结论),
24.在日常生活中,观察各种建筑物的地板,就能发现地板常用各种正多边形地砖铺砌成美丽的图案.也就是说,使用给定的某些正多边形,能够拼成一个平面图形,既不留下一丝空白,又不互相重叠(在几何里叫做平面镶嵌).这显然与正多边形的内角大小有关.当围绕一点拼在一起的几个多边形的内角加在一起恰好组成一个周角(360°)时,就拼成了一个平面图形.
(1)请根据下列图形,填写表中空格:
正多边形边数 3 4 5 6 … n
正多边形每个内角的度数 …
(2)如果只限于用一种正多边形镶嵌,哪几种正多边形能镶嵌成一个平面图形?
答案
一、选择题
D.B.C.C.D.C.C.B.C.A.
填空题
11.不能 12.2或4,2或1. 13.③. 14.ABC 15.ABC 16.6.
17.2n+2. 18.66,12n﹣6.
三、解答题
19.解:∵边长为1.2m的正六边形的地面的面积为:×1202×6=21600(cm2),
一块边长为20cm正六边形的瓷砖的面积为:×202×6=600(cm2),
一块边长为20cm的正三角形瓷砖的面积为:×202=100(cm2),
∴需要这样的正三角形瓷砖(21600﹣600)÷100=210块.
20.解:(1)用不同的多边形进行镶嵌,图形内部拼接在同一点处的各个角的和为360°,
故答案为:360;
(2)如图,
长方形的长为2cm、宽为1cm,若用4个这样的长方形镶嵌成1个大长方形,则该长方形周长的最小值是12(cm),
故答案为:12;
(3)七边形如图所示,
21.解:(1)∵正n边形的内角和为:180°(n﹣2),
∴每个内角的度数为:,
由题意得:m =360°,
整理得:m(n﹣2)=2n,
即:2m+2n=mn;
(2)边长相等的正三角形和正方形镶嵌平面,两种不同的摆放方案,如图所示:
(3)由题意得:++…+=360°,
整理得:++…+=2,
即:++…+=.
22.解:猜想1:①:,
整理,得 ②2x+3y=8,
整数解为③:
故答案为:,2x+3y=8,;
结论1:④1 ⑤2
故答案为1,2;
猜想2:能.
设围绕某一个点有x个正三角形和y个正六边形的内角可以拼成一个周角.根据题意可得方程,
整理得x+2y=6
所以;,
即2个正三角形和2个正六边形,或4个正三角形和1个正六边形.
23.解:第三类,
∵正六边形的每个内角的度数是120°,
∴在镶嵌平面时,围绕某一点有3个正六边形的内角可以拼成一个周角,所以用正六边形也可以进行平面图形的镶嵌;
第五类:设x个正三角形,y个正六边形,
则60x+120y=360,
x+2y=6,
正整数解是或,
即镶嵌平面时,在一个顶点周围围绕着2个正三角形和2个正六边形(或4个正三角形和1个正六边形)的内角可以拼成一个周角,所以用正三角形和正六边形可以进行平面镶嵌;
第六类:设x个正方形,y个正六边形,
则90x+120y+=360,
3x+4y=12,
此方程没有正整数解,
即镶嵌平面时,不能在一个顶点周围围绕着正方形和正六边形的内角拼成一个周角,所以不能用正方形和正六边形进行平面镶嵌;
第七类:设x个正三角形,y个正方形,z个正六边形,
则60x+90y+120z=360,
2x+3y+4z=12,
正整数解是,
即镶嵌平面时,在一个顶点周围围绕着1个正三角形、2个正方形、1个正六边的内角可以拼成一个周角,所以用正三角形、正方形、正六边形可以进行平面镶嵌.
24.解:(1)正三角形每个内角的度数是60°,
正四边形每个内角的度数是90°,
正五边形每个内角的度数是108°,
正六边形每个内角的度数是120°,
正n边形每个内角的度数是(180﹣)°.
故答案为:60°,90°,108°,120°,(180﹣)°;
(2)如限于用一种正多边形镶嵌,则由一顶点的周围角的和等于360°得正三角形、正四边形(或正方形)、正六边形都能镶嵌成一个平面图形.
一、选择题
1.用一些形状大小完全相同的图形不能镶嵌成平面图案的是( )
A.三角形 B.菱形 C.正六边形 D.正七边形
2.利用边长相等的正三角形和正六边形地砖能够铺满地板,若每个顶点处有a块正三角形和b块正六边形(a>b>0),则a+b的值为( )
A.4 B.5 C.6 D.7
3.下列正多边形的组合中,能够铺满地面的是( )
A.正六边形和正八边形 B.正四边形和正五边形
C.正三边形和正六边形 D.正四边形和正六边形
4.下列正多边形瓷砖中,若仅用种瓷砖铺地面,则不能将地面密铺的是( )
A.正三角形 B.正四边形 C.正五边形 D.正六边形
5.用正三角形和正方形组合能够铺满地面,每个顶点周围有m个正三角形和n个正方形(m、n为正整数),则m+n的值为( )
A.4 B.3 C.6 D.5
6.用形状、大小完全相同的下列图形,不能拼成既无缝隙又不重叠的图形的是( )
A.三角形 B.四边形 C.正五边形 D.正六边形
7.垦区小城镇建设如火如荼,小红家买了新楼.爸爸在正三角形、正方形、正五边形、正六边形四种瓷砖中,只购买一种瓷砖进行平铺,有几种购买方式( )
A.1种 B.2种 C.3种 D.4种
8.小飞家房屋装修时,选中了一种漂亮的正八边形地砖,建材店老板告诉她,只用一种八边形地砖是不能铺满地面的,但可以与另外一种形状的地砖混合使用,你认为要使地面铺满,小飞应选择另一种( )形状的地砖.
A.正三角形 B.正方形 C.正五边形 D.正六边形
9.正多边形通过镶嵌能够密铺成一个无缝隙的平面,下列组合中不能镶嵌成一个平面的是( )
A.正三角形和正方形 B.正三角形和正六边形
C.正方形和正六边形 D.正方形和正八边形
10.如图,某休闲广场是用边长相等的正四边形和正八边形的地砖组合,在每个顶点处无缝隙、无重叠的铺设,而且地砖完整.除此之外,还可以选择无缝隙、无重叠铺设的正多边形组合是( )
A.正三边形、正四边形 B.正四边形、正五边形
C.正五边形、正六边形 D.正六边形、正八边形
填空题
11.用一种正五边形或正八边形的瓷砖 铺满地面(填“能”或“不能”).
12.用正三角形和正六边形镶嵌,在每个顶点处有 个正三角形和 个正六边形,
13.现有①正三角形、②正方形、③正五边形三种形状的地砖,只选取其中一种地砖镶嵌地面,不能进行地面镶嵌的有 (填序号).
14.现有四种地面砖,它们的形状分别是:正三角形、正方形、正六边形、正八边形,且它们的边长都相等.同时选择其中两种地面砖密铺地面,选择的方式可以是 .
A.正三角形和正四边形
B.正三角形与正六边形
C.正方形与正八边形
D.正三角形与正八边形
15.下列正多边形组合中,能够铺满地面的是 .
A.正八边形和正方形
B.正三角形,正方形和正六边形
C.正三角形和正六边形
D.正方形和正六边形
16.如图所示是三个相同的正n边形拼成的无缝隙、不重叠的图形的一部分,则n的值为 .
17.如图,用灰白两色正方形瓷砖铺设地面,第1个图案用了4块灰色的瓷砖,第2个图案用了6块灰色的瓷砖,第3个图案用了8块灰色的瓷砖,…,第n个图案中灰色瓷砖块数为 .
18.如图是某广场用地板铺设的部分图案,中央是一块正六边形的地板砖,周围是正三角形和正方形的地板砖.从里向外的第1层包括6个正方形和6个正三角形,第2层包括6个正方形和18个正三角形,…,依此递推,则第6层中含有正三角形个数是 ,第n层中含有正三角形个数是 .
三、解答题
19.用若干块边长为20cm的正三角形瓷砖和一块边长为20cm正六边形的瓷砖铺成一边长为1.2m的正六边形的地面,则需要这样的正三角形瓷砖多少块?
20.用一些不重叠摆放的多边形把平面的一部分完全覆盖,叫做平面镶嵌(简称镶嵌).在生活中,我们运用镶嵌可以设计出美丽的图案.
(1)观察图①,我们发现:用不同的多边形进行镶嵌,图形内部拼接在同一点处的各个角的和为 °;
(2)如图②,长方形的长为2cm、宽为1cm,若用4个这样的长方形镶嵌成1个大长方形,则该长方形周长的最小值是 cm;
(3)如图③,用3个边长为1cm的正三角形和2个边长为1cm的正方形,可以镶嵌成1个七边形,请你画出该七边形的示意图.
21.在数学活动课上,研究用正多边形镶嵌平面.请解决以下问题:
(1)用一种正多边形镶嵌平面
例如,用6个全等的正三角形镶嵌平面,摆放方案如图所示:
若用m个全等的正n边形镶嵌平面,求出m,n应满足的关系式;
(2)用两种正多边形镶嵌平面
若这两种正多边形分别是边长相等的正三角形和正方形,请画出两种不同的摆放方案;
(3)用多种正多边形镶嵌平面
若镶嵌时每个顶点处的正多边形有n个,设这n个正多边形的边数分别为x1,x2,…,xn,求出x1,x2,…,xn应满足的关系式.(用含n的式子表示)
22.我们知道,可以单独用正三角形、正方形或正六边形铺满地面,如果我们要同时用两种不同的正多边形铺满地面,可以设计出几种不同的组合方案?
问题解决:
猜想1:是否可以同时用正方形、正八边形两种正多边形组合铺满地面?
验证1并完成填空:在铺地面时,设围绕某一个点有x个正方形和y个正八边形的内角可以拼成一个周角.根据题意:可得方程①: ,
整理得②: ,
我们可以找到方程的正整数解为③: .
结论1:铺满地面时,在一个顶点周围围绕着④ 个正方形和⑤ 个正八边形的内角可以拼成一个周角,所以同时用正方形和正八边形两种正多边形组合可以铺满地面.
猜想2:是否可以同时用正三角形和正六边形两种正多边形组合铺满地面?若能,请按照上述方法进行验证,并写出所有可能的方案;若不能,请说明理由.
23.数学问题:用边长相等的正三角形、正方形和正六边形能否进行平面图形的镶嵌?
问题探究:为了解决上述数学问题,我们采用分类讨论的思想方法去进行探究.
探究一:从正三角形、正方形和正六边形中任选一种图形,能否进行平面图形的镶嵌?
第一类:选正三角形.因为正三角形的每一个内角是60°,所以在镶嵌平面时,围绕某一点有6个正三角形的内角可以拼成一个周角,所以用正三角形可以进行平面图形的镶嵌.
第二类:选正方形.因为正方形的每一个内角是90°,所以在镶嵌平面时,围绕某一点有4个正方形的内角可以拼成一个周角,所以用正方形也可以进行平面图形的镶嵌.
第三类:选正六边形.(仿照上述方法,写出探究过程及结论)
探究二:从正三角形、正方形和正六边形中任选两种图形,能否进行平面图形的镶嵌?
第四类:选正三角形和正方形
在镶嵌平面时,设围绕某一点有x个正三角形和y个正方形的内角可以拼成个周角.根据题意,可得方程
60x+90y=360
整理,得2x+3y=12.
我们可以找到唯一组适合方程的正整数解为
镶嵌平面时,在一个顶点周围围绕着3个正三角形和2个正方形的内角可以拼成一个周角,所以用正三角形和正方形可以进行平面镶嵌
第五类:选正三角形和正六边形.(仿照上述方法,写出探究过程及结论)
第六类:选正方形和正六边形,(不写探究过程,只写出结论)
探究三:用正三角形、正方形和正六边形三种图形是否可以镶嵌平面?
第七类:选正三角形、正方形和正六边形三种图形.(不写探究过程,只写结论),
24.在日常生活中,观察各种建筑物的地板,就能发现地板常用各种正多边形地砖铺砌成美丽的图案.也就是说,使用给定的某些正多边形,能够拼成一个平面图形,既不留下一丝空白,又不互相重叠(在几何里叫做平面镶嵌).这显然与正多边形的内角大小有关.当围绕一点拼在一起的几个多边形的内角加在一起恰好组成一个周角(360°)时,就拼成了一个平面图形.
(1)请根据下列图形,填写表中空格:
正多边形边数 3 4 5 6 … n
正多边形每个内角的度数 …
(2)如果只限于用一种正多边形镶嵌,哪几种正多边形能镶嵌成一个平面图形?
答案
一、选择题
D.B.C.C.D.C.C.B.C.A.
填空题
11.不能 12.2或4,2或1. 13.③. 14.ABC 15.ABC 16.6.
17.2n+2. 18.66,12n﹣6.
三、解答题
19.解:∵边长为1.2m的正六边形的地面的面积为:×1202×6=21600(cm2),
一块边长为20cm正六边形的瓷砖的面积为:×202×6=600(cm2),
一块边长为20cm的正三角形瓷砖的面积为:×202=100(cm2),
∴需要这样的正三角形瓷砖(21600﹣600)÷100=210块.
20.解:(1)用不同的多边形进行镶嵌,图形内部拼接在同一点处的各个角的和为360°,
故答案为:360;
(2)如图,
长方形的长为2cm、宽为1cm,若用4个这样的长方形镶嵌成1个大长方形,则该长方形周长的最小值是12(cm),
故答案为:12;
(3)七边形如图所示,
21.解:(1)∵正n边形的内角和为:180°(n﹣2),
∴每个内角的度数为:,
由题意得:m =360°,
整理得:m(n﹣2)=2n,
即:2m+2n=mn;
(2)边长相等的正三角形和正方形镶嵌平面,两种不同的摆放方案,如图所示:
(3)由题意得:++…+=360°,
整理得:++…+=2,
即:++…+=.
22.解:猜想1:①:,
整理,得 ②2x+3y=8,
整数解为③:
故答案为:,2x+3y=8,;
结论1:④1 ⑤2
故答案为1,2;
猜想2:能.
设围绕某一个点有x个正三角形和y个正六边形的内角可以拼成一个周角.根据题意可得方程,
整理得x+2y=6
所以;,
即2个正三角形和2个正六边形,或4个正三角形和1个正六边形.
23.解:第三类,
∵正六边形的每个内角的度数是120°,
∴在镶嵌平面时,围绕某一点有3个正六边形的内角可以拼成一个周角,所以用正六边形也可以进行平面图形的镶嵌;
第五类:设x个正三角形,y个正六边形,
则60x+120y=360,
x+2y=6,
正整数解是或,
即镶嵌平面时,在一个顶点周围围绕着2个正三角形和2个正六边形(或4个正三角形和1个正六边形)的内角可以拼成一个周角,所以用正三角形和正六边形可以进行平面镶嵌;
第六类:设x个正方形,y个正六边形,
则90x+120y+=360,
3x+4y=12,
此方程没有正整数解,
即镶嵌平面时,不能在一个顶点周围围绕着正方形和正六边形的内角拼成一个周角,所以不能用正方形和正六边形进行平面镶嵌;
第七类:设x个正三角形,y个正方形,z个正六边形,
则60x+90y+120z=360,
2x+3y+4z=12,
正整数解是,
即镶嵌平面时,在一个顶点周围围绕着1个正三角形、2个正方形、1个正六边的内角可以拼成一个周角,所以用正三角形、正方形、正六边形可以进行平面镶嵌.
24.解:(1)正三角形每个内角的度数是60°,
正四边形每个内角的度数是90°,
正五边形每个内角的度数是108°,
正六边形每个内角的度数是120°,
正n边形每个内角的度数是(180﹣)°.
故答案为:60°,90°,108°,120°,(180﹣)°;
(2)如限于用一种正多边形镶嵌,则由一顶点的周围角的和等于360°得正三角形、正四边形(或正方形)、正六边形都能镶嵌成一个平面图形.
