17.1 勾股定理 课时1 教案
图片预览

文档简介
中小学教育资源及组卷应用平台
第17章《勾股定理》教案
17.1 勾股定理
第1课时
教学目标:
了解勾股定理的发现过程,理解并掌握勾股定理的内容,会用面积法证明勾股定理,能应用勾股定理进行简单的计算.
重点:
勾股定理的内容和证明及简单应用.
难点:
勾股定理的应用.
教学流程:
一、导入新课
相传2500多年前,古希腊著名数学家毕哥拉斯有一次在朋友家作客时,发现朋友家用砖铺成的地面图案反映了直角三角形三边的某种数量关系.
同学们,地砖图案中蕴含着怎样的数量关系呢,让我们一起探索吧。
二、新课讲解
思考:图中三个正方形 的面积有什么关系?等腰直角三角形的三边有什么关系?
(观看视频演示)
答:两个小正方形的面积这和等于大正方形的面积.
等腰直角三角形的三边满足斜边的平方等于两直角边的平方和.
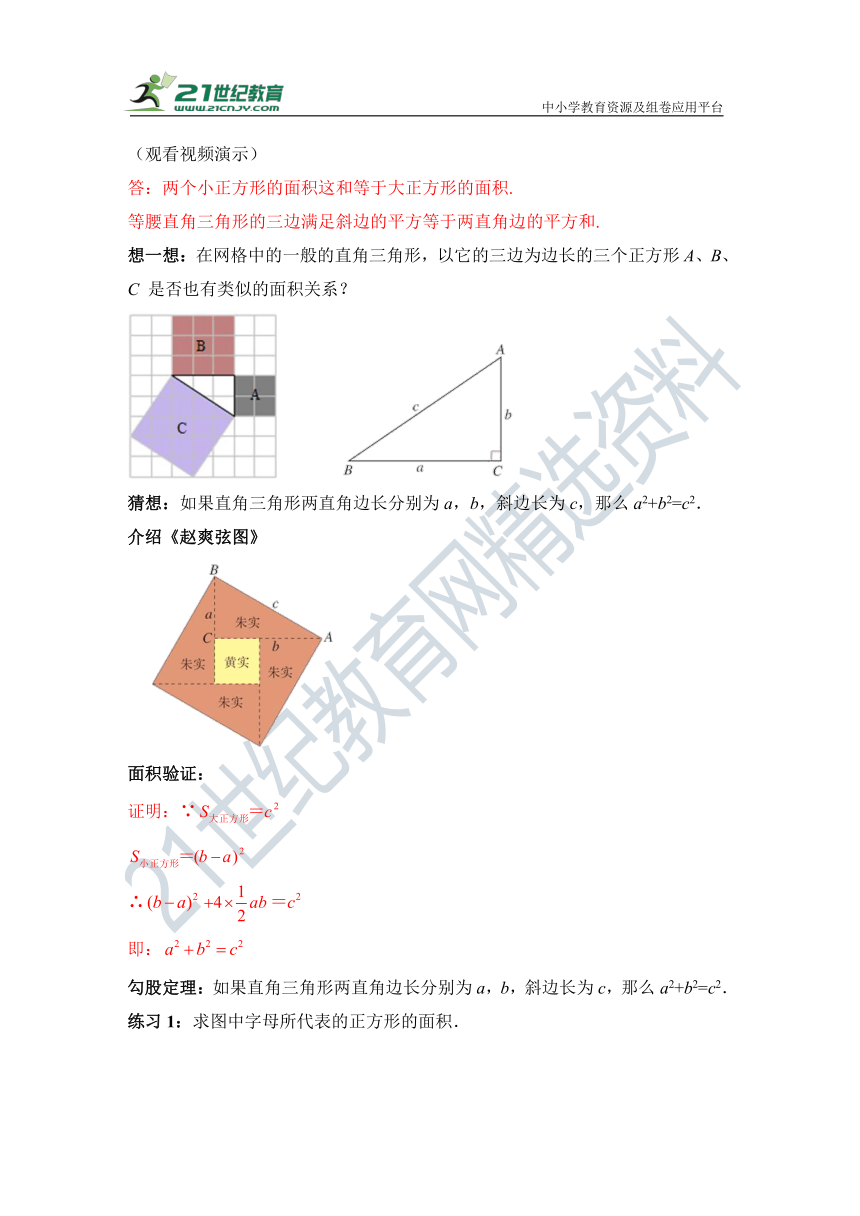
想一想:在网格中的一般的直角三角形,以它的三边为边长的三个正方形A、B、C 是否也有类似的面积关系?
猜想:如果直角三角形两直角边长分别为a,b,斜边长为c,那么a2+b2=c2.
介绍《赵爽弦图》
面积验证:
证明:∵
∴
即:
勾股定理:如果直角三角形两直角边长分别为a,b,斜边长为c,那么a2+b2=c2.
练习1:求图中字母所代表的正方形的面积.
答案:(1)81;(2)56,80;(3)225
练习2:求下列直角三角形中未知边的长度.
答案:(1);(2)
三、巩固提升
1.下列说法正确的是( )
A.若a,b,c是△ABC的三边,则a2+b2=c2
B.若a,b,c是Rt△ABC的三边,则a2+b2=c2
C.若a,b,c是Rt△ABC的三边,∠A=90°,则a2+b2=c2
D.若a,b,c是Rt△ABC的三边,∠C=90°,则a2+b2=c2
答案:D
2.利用如图(1)或(2)所示的两个图形中的有关面积的等量关系都能证明数学中一个十分著名的定理,这个定理称为_________,该定理中结论的数学表达式是__________.
答案:勾股定理,a2+b2=c2
3.如图,正方形B的面积是______.
答案:144
4.求图中直角三角形中未知边的长度:c=_____,b=_____.
答案:15,12
5.在△ABC中,∠C=90°,∠A,∠B,∠C的对边分别是a,b,c.
(1)若b=2,c=3,求a的值;
(2)若a∶c=3∶5,b=28,求a,c的值.
解:(1)在Rt△ABC中,由勾股定理得,
(2)设a=3x,c=5x,
∵a2+b2=c2,
∴(3x)2+282=(5x)2,解得x=7,
∴a=21,c=35
四、课堂小结
今天我们学习了哪些知识?
勾股定理的内容是什么?它有什么作用?
五、布置作业
教材P28页习题17.1第1、2题.
第17章《勾股定理》教案
17.1 勾股定理
第1课时
教学目标:
了解勾股定理的发现过程,理解并掌握勾股定理的内容,会用面积法证明勾股定理,能应用勾股定理进行简单的计算.
重点:
勾股定理的内容和证明及简单应用.
难点:
勾股定理的应用.
教学流程:
一、导入新课
相传2500多年前,古希腊著名数学家毕哥拉斯有一次在朋友家作客时,发现朋友家用砖铺成的地面图案反映了直角三角形三边的某种数量关系.
同学们,地砖图案中蕴含着怎样的数量关系呢,让我们一起探索吧。
二、新课讲解
思考:图中三个正方形 的面积有什么关系?等腰直角三角形的三边有什么关系?
(观看视频演示)
答:两个小正方形的面积这和等于大正方形的面积.
等腰直角三角形的三边满足斜边的平方等于两直角边的平方和.
想一想:在网格中的一般的直角三角形,以它的三边为边长的三个正方形A、B、C 是否也有类似的面积关系?
猜想:如果直角三角形两直角边长分别为a,b,斜边长为c,那么a2+b2=c2.
介绍《赵爽弦图》
面积验证:
证明:∵
∴
即:
勾股定理:如果直角三角形两直角边长分别为a,b,斜边长为c,那么a2+b2=c2.
练习1:求图中字母所代表的正方形的面积.
答案:(1)81;(2)56,80;(3)225
练习2:求下列直角三角形中未知边的长度.
答案:(1);(2)
三、巩固提升
1.下列说法正确的是( )
A.若a,b,c是△ABC的三边,则a2+b2=c2
B.若a,b,c是Rt△ABC的三边,则a2+b2=c2
C.若a,b,c是Rt△ABC的三边,∠A=90°,则a2+b2=c2
D.若a,b,c是Rt△ABC的三边,∠C=90°,则a2+b2=c2
答案:D
2.利用如图(1)或(2)所示的两个图形中的有关面积的等量关系都能证明数学中一个十分著名的定理,这个定理称为_________,该定理中结论的数学表达式是__________.
答案:勾股定理,a2+b2=c2
3.如图,正方形B的面积是______.
答案:144
4.求图中直角三角形中未知边的长度:c=_____,b=_____.
答案:15,12
5.在△ABC中,∠C=90°,∠A,∠B,∠C的对边分别是a,b,c.
(1)若b=2,c=3,求a的值;
(2)若a∶c=3∶5,b=28,求a,c的值.
解:(1)在Rt△ABC中,由勾股定理得,
(2)设a=3x,c=5x,
∵a2+b2=c2,
∴(3x)2+282=(5x)2,解得x=7,
∴a=21,c=35
四、课堂小结
今天我们学习了哪些知识?
勾股定理的内容是什么?它有什么作用?
五、布置作业
教材P28页习题17.1第1、2题.
