数学人教A版(2019)必修第一册4.3.1对数的概念 课件(共18张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第一册4.3.1对数的概念 课件(共18张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-06 14:21:23 | ||
图片预览




文档简介
(共18张PPT)
4.3 对数
4.3.1 对数的概念
人教A版2019高中数学必修第一册
问题引入
问题 请计算下面的式子。(不使用计算器)
问题引入
在16世纪,随着哥白尼“日心说”的盛行。天文学也蓬勃发展,欧洲人渐渐热衷于地理探险和海洋贸易,特别是地理探险需要更准确的天文知识。需要对庞大的“天文数据”进行快速和准确的计算。但那时候还没有计算机,人们迫切需要找到一种方法提高运算效率,那么该怎么办呢?
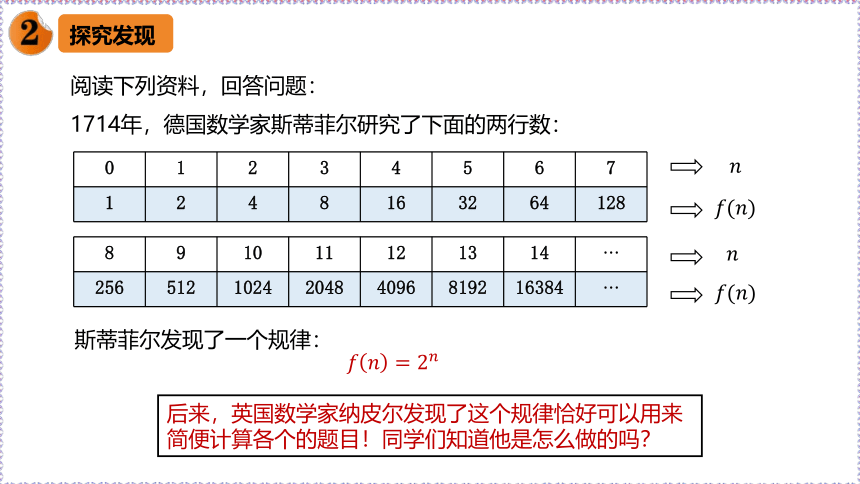
阅读下列资料,回答问题:
1714年,德国数学家斯蒂菲尔研究了下面的两行数:
探究发现
0 1 2 3 4 5 6 7
1 2 4 8 16 32 64 128
8 9 10 11 12 13 14
256 512 1024 2048 4096 8192 16384
斯蒂菲尔发现了一个规律:
后来,英国数学家纳皮尔发现了这个规律恰好可以用来简便计算各个的题目!同学们知道他是怎么做的吗?
探究发现
0 1 2 3 4 5 6 7
1 2 4 8 16 32 64 128
8 9 10 11 12 13 14
256 512 1024 2048 4096 8192 16384
关键:把每个整数转化为
这样一来,就可以将整数的乘法、除法、乘方、开方转化为对应指数的加法、减法、乘法、除法。
探究发现
0 1 2 3 4 5 6 7
1 2 4 8 16 32 64 128
8 9 10 11 12 13 14
256 512 1024 2048 4096 8192 16384
关键:把每个整数转化为
这样一来,就可以将整数的乘法、除法、乘方、开方转化为对应指数的加法、减法、乘法、除法。
能不能
写成?
探究发现
能不能
写成?
探究发现
0 1 2 3 4 5 6 7
1 2 4 8 16 32 64 128
8 9 10 11 12 13 14
256 512 1024 2048 4096 8192 16384
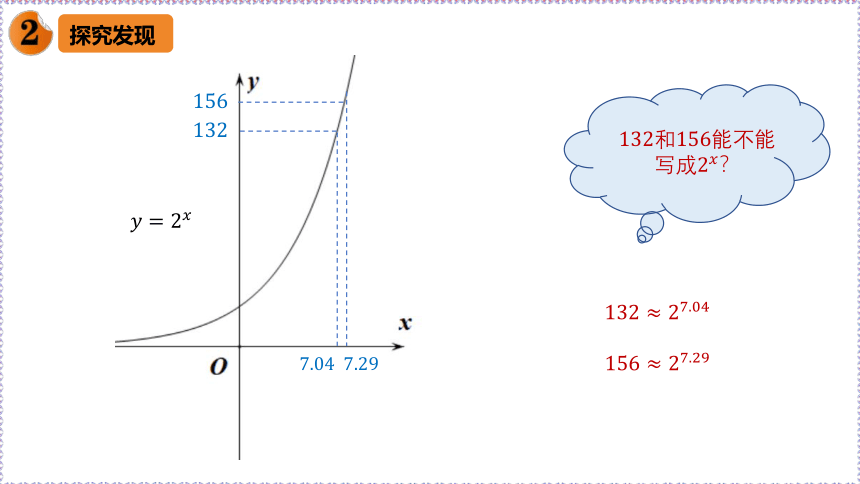
如果要计算,还能否用同样的方法解决呢?
0 1 2 3 4 5 6 7 7.04 7.29
1 2 4 8 16 32 64 128 132 156
8 9 10 11 12 13 14 14.33
256 512 1024 2048 4096 8192 16384 20592
受到斯蒂菲尔表格的启发,英国数学家纳皮尔编制出了类似的表格,不过他所选取的底数不是2,而是一个比较复杂的数。后来英国数学家布里格斯根据人们使用十进制的习惯,花了大量时间精力,终于在1617年编制了以10为底的表格,以供人们计算较大的数据。
布里格斯编写的表格(部分)
以10为底 以10为底
1 0.00000 8 0. 90308998699194
2 0.30102999566398 9 0.95424250943932
3 0. 47712125471966 10 1. 0000000000000
4 0. 60205999132796 11 1.04139268515822
5 0. 69897000433602 12 1.07918124604762
6 0.77815125038364 13 1.11394335230683
7 0.84509804001426
编制表格的关键:对于每个,令,再把表示出来
编制表格的关键:对于每个,把写成:
(以2为底)
(以10为底)
一般地,可以以为底,把写成且
如何把准确表示出来呢?
形成概念
观察数的运算的发展,思考问题:
(1)已知,求
(2)已知,求
(3)已知,求
(4)已知,求
对数
形成概念
【对数的定义】 一般地,如果,那么数叫做以为底的对数,记作 ,其中叫做对数的底数, 叫做真数
根据定义,可以得到对数与指数间的关系:
当时,
负数与零没有对数
对数是指数的逆运算
形成概念
【对数的定义】 一般地,如果,那么数叫做以为底的对数,记作 ,其中叫做对数的底数, 叫做真数
我们将以10为底的对数叫做常用对数,并把 记为
将以e为底的对数叫做自然对数,并把 记为
根据对数的定义,计算:
(1)
(2)
(3)
(4)
解:(1)
(2)
(3)
(4)
将整数的乘法、除法、乘方、开方转化为对应指数的加法、减法、乘法、除法
化归思想
一般地,可以以为底,把写成且即 ,如何把准确表示出来呢?
课堂小结
(1)已知,求
(2)已知,求
(3)已知,求
(4)已知,求
对数
类比思想
对数是一个数!
课堂小结
课后作业
1、完成课本课后习题
2、思考:为什么对数的底数和真数要满足
4.3 对数
4.3.1 对数的概念
人教A版2019高中数学必修第一册
问题引入
问题 请计算下面的式子。(不使用计算器)
问题引入
在16世纪,随着哥白尼“日心说”的盛行。天文学也蓬勃发展,欧洲人渐渐热衷于地理探险和海洋贸易,特别是地理探险需要更准确的天文知识。需要对庞大的“天文数据”进行快速和准确的计算。但那时候还没有计算机,人们迫切需要找到一种方法提高运算效率,那么该怎么办呢?
阅读下列资料,回答问题:
1714年,德国数学家斯蒂菲尔研究了下面的两行数:
探究发现
0 1 2 3 4 5 6 7
1 2 4 8 16 32 64 128
8 9 10 11 12 13 14
256 512 1024 2048 4096 8192 16384
斯蒂菲尔发现了一个规律:
后来,英国数学家纳皮尔发现了这个规律恰好可以用来简便计算各个的题目!同学们知道他是怎么做的吗?
探究发现
0 1 2 3 4 5 6 7
1 2 4 8 16 32 64 128
8 9 10 11 12 13 14
256 512 1024 2048 4096 8192 16384
关键:把每个整数转化为
这样一来,就可以将整数的乘法、除法、乘方、开方转化为对应指数的加法、减法、乘法、除法。
探究发现
0 1 2 3 4 5 6 7
1 2 4 8 16 32 64 128
8 9 10 11 12 13 14
256 512 1024 2048 4096 8192 16384
关键:把每个整数转化为
这样一来,就可以将整数的乘法、除法、乘方、开方转化为对应指数的加法、减法、乘法、除法。
能不能
写成?
探究发现
能不能
写成?
探究发现
0 1 2 3 4 5 6 7
1 2 4 8 16 32 64 128
8 9 10 11 12 13 14
256 512 1024 2048 4096 8192 16384
如果要计算,还能否用同样的方法解决呢?
0 1 2 3 4 5 6 7 7.04 7.29
1 2 4 8 16 32 64 128 132 156
8 9 10 11 12 13 14 14.33
256 512 1024 2048 4096 8192 16384 20592
受到斯蒂菲尔表格的启发,英国数学家纳皮尔编制出了类似的表格,不过他所选取的底数不是2,而是一个比较复杂的数。后来英国数学家布里格斯根据人们使用十进制的习惯,花了大量时间精力,终于在1617年编制了以10为底的表格,以供人们计算较大的数据。
布里格斯编写的表格(部分)
以10为底 以10为底
1 0.00000 8 0. 90308998699194
2 0.30102999566398 9 0.95424250943932
3 0. 47712125471966 10 1. 0000000000000
4 0. 60205999132796 11 1.04139268515822
5 0. 69897000433602 12 1.07918124604762
6 0.77815125038364 13 1.11394335230683
7 0.84509804001426
编制表格的关键:对于每个,令,再把表示出来
编制表格的关键:对于每个,把写成:
(以2为底)
(以10为底)
一般地,可以以为底,把写成且
如何把准确表示出来呢?
形成概念
观察数的运算的发展,思考问题:
(1)已知,求
(2)已知,求
(3)已知,求
(4)已知,求
对数
形成概念
【对数的定义】 一般地,如果,那么数叫做以为底的对数,记作 ,其中叫做对数的底数, 叫做真数
根据定义,可以得到对数与指数间的关系:
当时,
负数与零没有对数
对数是指数的逆运算
形成概念
【对数的定义】 一般地,如果,那么数叫做以为底的对数,记作 ,其中叫做对数的底数, 叫做真数
我们将以10为底的对数叫做常用对数,并把 记为
将以e为底的对数叫做自然对数,并把 记为
根据对数的定义,计算:
(1)
(2)
(3)
(4)
解:(1)
(2)
(3)
(4)
将整数的乘法、除法、乘方、开方转化为对应指数的加法、减法、乘法、除法
化归思想
一般地,可以以为底,把写成且即 ,如何把准确表示出来呢?
课堂小结
(1)已知,求
(2)已知,求
(3)已知,求
(4)已知,求
对数
类比思想
对数是一个数!
课堂小结
课后作业
1、完成课本课后习题
2、思考:为什么对数的底数和真数要满足
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
