2023-2024学年九年级数学上册(沪教版)24.2比例线段(第2课时)课件(共38张PPT)
文档属性
| 名称 | 2023-2024学年九年级数学上册(沪教版)24.2比例线段(第2课时)课件(共38张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 20.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-07 14:35:31 | ||
图片预览











文档简介
(共38张PPT)
24.2比例线段(第2课时)-黄金分割
第24章 相似三角形
教师
xxx
沪教版 九年级第一学期
黄金分割
黄金分割的应用
黄金分割点的讨论
01
03
02
CONTANTS
目 录
黄金分割
01
知识精讲
情境引入
凡是美的东西,都有共同的特征,这就是部分与部分以及部分与整体之间的协调一致
——毕达哥拉斯
情景引入
情境引入
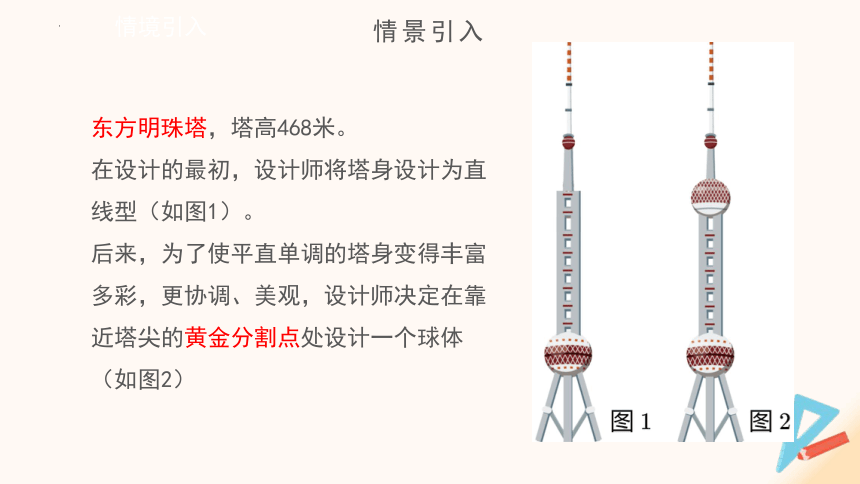
东方明珠塔,塔高468米。
在设计的最初,设计师将塔身设计为直线型(如图1)。
后来,为了使平直单调的塔身变得丰富多彩,更协调、美观,设计师决定在靠近塔尖的黄金分割点处设计一个球体(如图2)
情景引入
情境引入
0
我们可以建立如图所示的数学模型,度量图中线段AB、AC的长度,并计算线段AB与AC、BC与AB的比值.
东
方
明
珠
塔
“黄金分割点”究竟特别在哪里呢?
计算可得:
AB:AC≈0.62
BC:AB≈0.62
推测:
AB:AC=BC:AB
探究新知
芭蕾舞演员表演时,身体各部分之间适当的比例给人以匀称、协调的美感。
为什么舞台上翩翩起舞的芭蕾舞演员要踮起脚尖呢?
因为踮起脚尖可以让芭蕾舞演员的下半身显得更加修长,给人以匀称、协调的美感。
探究新知
让我们从数学角度来分析“这种美感”产生的根源
度量图中线段AB、AC的长度,并计算线段AB与AC、BC与AB的比值.
计算可得:
AB:AC≈0.62
BC:AB≈0.62
推测:
AB:AC=BC:AB
探究新知
知识精讲
01
古希腊数学家、天文学家欧多克赛斯提出一个问题∶
能否将一条线段 AB分成不相等的两部分,使较短的线段BC与较长线段AC的比等于AC与原线段AB的比?(如图)
解:设AB=“1”,AC=x,则BC=AB-AC=1-x
由=,得:=x,即x +x-1=0
解得:x1=,x2=(不合题意,舍去)
∴AC=,∴==
探究新知
A
C
B
其近似值为 0.618.
如果其中较长线段
AC与AB的比
为全线段与较短线段的比例中项,
如图,已知线段AB长度为a ,点C是AB上一点,且使 AB:AC=AC:PB.求线段AC的长和 的值.
AC
AB
比值
如图,点 C 把线段AB
这样的线段分割叫做
分割点叫做这条线段的
黄金分割,
黄金分割点,
黄金数,
概念学习:
AB
AC
=
AC
BC
( 或 AC2=AB·BC ),
( 或BC与AC的比 )
叫做黄金比.
AC
AB
BC
AC
A
C
B
分成两条线段 AC 和 BC
(AC>BC),
即
叫做
=
=
或
即
探究新知
从黄金分割的定义上理解:
从比值上理解黄金比:
较长线段
全线段
全线段
较长线段
较长线段
较短线段
=
=
较短线段
较长线段
=
理解定义
A
C
B
较长线段2
= 全线段×较短线段
或
其近似值为 0.618.
如果其中较长线段
AC与AB的比
为全线段与较短线段的比例中项,
比值
如图,点 C 把线段AB
这样的线段分割叫做
分割点叫做这条线段的
黄金分割,
黄金分割点,
黄金数,
AB
AC
=
AC
BC
( 或 AC2=AB·BC ),
( 或BC与AC的比 )
叫做黄金比.
分成两条线段 AC 和 BC
(AC>BC),
即
叫做
AC
AB
BC
AC
=
=
或
即
探究新知
知识精讲
议一议:“黄金分割”在生活中还有哪些应用呢?
数学课本是长方形,其宽与长的比约为0.618
一片树叶也蕴含着“黄金分割”
鹦鹉螺外壳,其每圈螺纹的直径与相邻螺纹直径的比约为0.618
……
探究新知
黄金分割点的讨论
02
议一议:一条线段有几个黄金分割点?以线段AC为例
∴线段的黄金分割点有两个
A
C
【分析】
设B为黄金分割点
①若B1靠近点A(AB1②若B2靠近点C(AB2>BC)
B1
B2
探究新知
议一议:已知AC的长度,点B为线段AC的黄金分割点,求AB的长度
【分析】
B点有两种可能性,需分类讨论
A
C
B1
B2
①AB1∵点B为线段AC的黄金分割点
∴=
∴==1-=1-=
∴AB=(1-)AC=AC
②AB2>BC2
∵点B为线段AC的黄金分割点
∴=
∴AB=AC
探究新知
【题型:求线段的长】
已知AC的长度,点B为线段AC的黄金分割点,求AB的长度
①ABBC时AB=AC
题型总结
探究新知
1、过点B作BC⊥AB,
用尺规作图找出黄金分割点
2、连接AC,
3、以点A为圆心、AE为半径画弧,
1
.
2
AB
BC
=
A
B
C
E
P
你能说明这样作图的道理吗?
如图,给定一条线段AB,如何找出它的黄金分割点呢?
操 作
交AC于点E;
交AB于点P.
则点P即为所求.
我们通过如下作图来达到要求:
并在垂线上截取
以点C为圆心、CB为半径画弧,
探究新知
全线段
较长线段
较长线段
较短线段
=
较长线段
全线段
=
较短线段
较长线段
=
较长线段2
= 全线段×较短线段
或
如何判断某点是线段的黄金分割点?
归纳总结
①
②
③
探究新知
1、已知点C在线段AB上,且C是线段AB的黄金分割点(AC>BC),则下列结论正确的是( )
A. AB2=AC·BC B. BC2=AC·AB
C. AC= BC
D. BC= AC
D
课堂练习
2、上海东方明珠电视塔高468m,上球体是塔身的黄金分割点,它到塔底部的距离大约是多少米(精确到0.1m)?
468m
= 468×0.618
较长线段
全线段
=
较长线段
=
×全线段
468×
≈ 289.2
(m)
方法技巧:
课堂练习
3、已知线段 AB=6cm,点P为线段AB的黄金分割点,求线段AP的长.
解:
① 当 AP>BP 时,
AP=
较长线段
全线段
=
较长线段
=
×全线段
AB
=
(cm)
② 当 APBP=
AB
=
(cm)
较短线段=
全线段 -
较长线段
∴ AP=
AB-BP=
6-
=
(cm)
综上所述:
线段 AP的长为 cm 或 cm.
方法技巧:
=
=
×6
×6
课堂练习
5、【2018春 常熟市期末】如图,已知点C是线段AB的黄金分割点,且BC>AC.若S1表示以BC为边的正方形面积,S2表示长为AB、宽为AC的矩形面积,则S1与S2的大小关系为( )
4、演员报幕时应站在舞台的黄金分割处,若舞台长10米,则演员应站在距舞台一端 米远的地方.
A.S1>S2 B.S1=S2
C.S1<S2 D.不能确定
或
B
课堂练习
6、在人体躯干(脚底到肚脐的长度)与身高的比例上,肚脐是理想的黄金分割点,即比例越接近0.618,越给人以美感.张女士原来脚底到肚脐的长度与身高的比为0.60,她的身高为1.60m,她应该选择多高的高跟鞋穿上看起来更美?(精确到十分位)
解:
由题意可得,
下半身长是 160×0.6=96 (cm)
设选择的高跟鞋的高度是xcm.
96+x
160+x
=
即
96+x
160+x
=0.168
解得
x≈7.5
∴ 她应该选择7.5cm左右的高跟鞋穿上看起来更美.
根据黄金分割的定义,得
课堂练习
7、如图,在五角星形中,AD=BC,C,D两点都是AB的黄金分割点,AB=1,求CD的长.
解:
∵ C、D两点都是AB的黄金分割点
BD=
AB
=
∴ AC=
∴ AD=
AB-BD=
1-
∵ AD=BC
∴ AD=BC
∴ CD=
AB-AD-BC
=1-
课堂练习
8、如图所示,以长为2的定线段AB为边作正方形ABCD,取AB的中点P,连接PD,在BA的延长线上取点F,使PF=PD,以AF为边作正方形AMEF,点M在AD上.
(1) 求AM,DM的长;
(2) 点M是AD的黄金分割点吗?为什么?
2
1
课堂练习
黄金分割的应用
03
宽与长的比
巴台农神庙
(Parthenom Temple)
F
C
A
E
B
D
如果把图中用虚线表示的矩形画成如图所示的矩形ABCD,以矩形ABCD 的宽为边在其内部作正方形AEFD,那么我们可以惊奇地发现 , 点E是AB 的黄金分割点吗?矩形ABCD的宽与长的比是黄金比吗?为什么
BE
BC
=
BC
AB
这种矩形给人以美感.
等于黄金比的矩形
也称为黄金矩形.
概念学习:
黄金矩形
探究新知
练习:矩形的长和宽分别为 a 和 b,下列数据能构成黄金矩形的是( )
A. a=4,b=
B. a=4,b=
C. a=2,b=
D. a=2,b=
D
宽与长的比
等于黄金比的矩形
也称为黄金矩形.
探究新知
追溯历史文化
早在古希腊,数学家、天文学家欧多克索斯(Eudoxus,约前400——前347)曾提出:能否将一条线段分成不相等的两部分,使较短线段与较长线段的比等于较长线段与原线段的比?这就是黄金分割问题.
而发现黄金分割的是古希腊哲学家毕达哥拉斯。一天,毕达哥拉斯从一家铁匠铺路过,被铺子中那有节奏的叮叮当当的打铁声所吸引,便站在那里仔细聆听,似乎这声音中隐匿着什么秘密。他走进作坊,拿出一把尺量了一下铁锤和铁砧的尺寸,发现它们之间存在着一种十分和谐的关系。回到家里,毕达哥拉斯拿出一根线,想将它分为两段。怎样分才最好呢?经过反复比较,他最后确定0.618 :1的比例截断最优美。后来,意大利著名科学家、艺术家达·芬奇给这个比例冠以“黄金”二字的美名。
天文学家开普勒(Johannes Kepler,1571——1630)把这种分割线段的方法称为神圣分割,并指出,毕达哥拉斯定理(勾股定理)和黄金分割“是几何中的双宝,前者好比黄金,后者堪称珠玉”。 而历史上最早正式在书中使用“黄金分割”这个名称的是欧姆(Martin Ohm,1792——1872)。19世纪以后,“黄金分割”的说法逐渐流行起来… …
探究新知
人与黄金分割
人体肚脐不但是黄金点美化身型,有时还是医疗效果黄金点,许多民间名医在肚脐上贴药治好了某些疾病。人体最感舒适的温度是23℃(体温),也是正常人体温(37℃)的黄金点(23=37×0.618)。这说明医学与0.618有千丝万缕联系,尚待开拓研究。人体还有几个黄金点:肚脐上部分的黄金点在咽喉,肚脐以下部分的黄金点在膝盖,上肢的黄金点在肘关节。上肢与下肢长度之比均近似0.618.
探究新知
在人的面部,五官的分布越符合黄金分割,看起来就越美.
B
C
A
人与黄金分割
探究新知
绘画艺术中的黄金分割
著名画家达 芬奇的蒙娜丽莎构图就完美的体现了黄金分割在油画艺术上的应用。通过下面两幅图片可以看出来,蒙娜丽莎的头和两肩在整幅画面中都处于完美的体现了黄金分割,使得这幅油画看起来是那么的和谐和完美.
探究新知
雕塑--维纳斯
雕塑断臂女神维纳斯的体型完全与黄金比相符,即以人的肚脐为分界点,上身与下身之比,或者说下身与全身之比约是0.618 这样的身体给人的感觉就是非常的匀称,充满着美感.
建筑中的神秘数字
探究新知
建筑中的神秘数字
知道这是什么地方吗?
文明古国埃及的金字塔,形似方锥,大小各异。高(137米)与底边长(227米)之比为0.629,但这些金字塔底面的边长与高这比都接近于0.618.
探究新知
巴黎圣母院
联合国总部大厦
古希腊巴台农神庙
黄金分割,尤其宽与长的比为黄金比的矩形,在古典及现代建筑中都有广泛的应用.
建筑中的神秘数字
武器装备与黄金分割
当发射子弹的步枪刚刚制造出来的时候,它的枪把和枪身的长度比例很不科学合理,很不方便于抓握和瞄准。到了1918年,一个名叫阿尔文·约克的美远征军下士,对这种步枪进行了改造,改进后的枪型枪身和枪把的比例恰恰符合0.618的比例。
探究新知
黄金分割
点C把线段AB分成两条线段AC和BC,如果 , 那么称线段AB被点C黄金分割.点C叫做线段AB的黄金分割点,AC与AB的比称为黄金比.
黄金分割点:一条线段有两个黄金分割点
黄金比:较长线段:原线段 =
定义
课堂小结
感谢观看
24.2比例线段(第2课时)-黄金分割
第24章 相似三角形
教师
xxx
沪教版 九年级第一学期
黄金分割
黄金分割的应用
黄金分割点的讨论
01
03
02
CONTANTS
目 录
黄金分割
01
知识精讲
情境引入
凡是美的东西,都有共同的特征,这就是部分与部分以及部分与整体之间的协调一致
——毕达哥拉斯
情景引入
情境引入
东方明珠塔,塔高468米。
在设计的最初,设计师将塔身设计为直线型(如图1)。
后来,为了使平直单调的塔身变得丰富多彩,更协调、美观,设计师决定在靠近塔尖的黄金分割点处设计一个球体(如图2)
情景引入
情境引入
0
我们可以建立如图所示的数学模型,度量图中线段AB、AC的长度,并计算线段AB与AC、BC与AB的比值.
东
方
明
珠
塔
“黄金分割点”究竟特别在哪里呢?
计算可得:
AB:AC≈0.62
BC:AB≈0.62
推测:
AB:AC=BC:AB
探究新知
芭蕾舞演员表演时,身体各部分之间适当的比例给人以匀称、协调的美感。
为什么舞台上翩翩起舞的芭蕾舞演员要踮起脚尖呢?
因为踮起脚尖可以让芭蕾舞演员的下半身显得更加修长,给人以匀称、协调的美感。
探究新知
让我们从数学角度来分析“这种美感”产生的根源
度量图中线段AB、AC的长度,并计算线段AB与AC、BC与AB的比值.
计算可得:
AB:AC≈0.62
BC:AB≈0.62
推测:
AB:AC=BC:AB
探究新知
知识精讲
01
古希腊数学家、天文学家欧多克赛斯提出一个问题∶
能否将一条线段 AB分成不相等的两部分,使较短的线段BC与较长线段AC的比等于AC与原线段AB的比?(如图)
解:设AB=“1”,AC=x,则BC=AB-AC=1-x
由=,得:=x,即x +x-1=0
解得:x1=,x2=(不合题意,舍去)
∴AC=,∴==
探究新知
A
C
B
其近似值为 0.618.
如果其中较长线段
AC与AB的比
为全线段与较短线段的比例中项,
如图,已知线段AB长度为a ,点C是AB上一点,且使 AB:AC=AC:PB.求线段AC的长和 的值.
AC
AB
比值
如图,点 C 把线段AB
这样的线段分割叫做
分割点叫做这条线段的
黄金分割,
黄金分割点,
黄金数,
概念学习:
AB
AC
=
AC
BC
( 或 AC2=AB·BC ),
( 或BC与AC的比 )
叫做黄金比.
AC
AB
BC
AC
A
C
B
分成两条线段 AC 和 BC
(AC>BC),
即
叫做
=
=
或
即
探究新知
从黄金分割的定义上理解:
从比值上理解黄金比:
较长线段
全线段
全线段
较长线段
较长线段
较短线段
=
=
较短线段
较长线段
=
理解定义
A
C
B
较长线段2
= 全线段×较短线段
或
其近似值为 0.618.
如果其中较长线段
AC与AB的比
为全线段与较短线段的比例中项,
比值
如图,点 C 把线段AB
这样的线段分割叫做
分割点叫做这条线段的
黄金分割,
黄金分割点,
黄金数,
AB
AC
=
AC
BC
( 或 AC2=AB·BC ),
( 或BC与AC的比 )
叫做黄金比.
分成两条线段 AC 和 BC
(AC>BC),
即
叫做
AC
AB
BC
AC
=
=
或
即
探究新知
知识精讲
议一议:“黄金分割”在生活中还有哪些应用呢?
数学课本是长方形,其宽与长的比约为0.618
一片树叶也蕴含着“黄金分割”
鹦鹉螺外壳,其每圈螺纹的直径与相邻螺纹直径的比约为0.618
……
探究新知
黄金分割点的讨论
02
议一议:一条线段有几个黄金分割点?以线段AC为例
∴线段的黄金分割点有两个
A
C
【分析】
设B为黄金分割点
①若B1靠近点A(AB1
B1
B2
探究新知
议一议:已知AC的长度,点B为线段AC的黄金分割点,求AB的长度
【分析】
B点有两种可能性,需分类讨论
A
C
B1
B2
①AB1
∴=
∴==1-=1-=
∴AB=(1-)AC=AC
②AB2>BC2
∵点B为线段AC的黄金分割点
∴=
∴AB=AC
探究新知
【题型:求线段的长】
已知AC的长度,点B为线段AC的黄金分割点,求AB的长度
①AB
题型总结
探究新知
1、过点B作BC⊥AB,
用尺规作图找出黄金分割点
2、连接AC,
3、以点A为圆心、AE为半径画弧,
1
.
2
AB
BC
=
A
B
C
E
P
你能说明这样作图的道理吗?
如图,给定一条线段AB,如何找出它的黄金分割点呢?
操 作
交AC于点E;
交AB于点P.
则点P即为所求.
我们通过如下作图来达到要求:
并在垂线上截取
以点C为圆心、CB为半径画弧,
探究新知
全线段
较长线段
较长线段
较短线段
=
较长线段
全线段
=
较短线段
较长线段
=
较长线段2
= 全线段×较短线段
或
如何判断某点是线段的黄金分割点?
归纳总结
①
②
③
探究新知
1、已知点C在线段AB上,且C是线段AB的黄金分割点(AC>BC),则下列结论正确的是( )
A. AB2=AC·BC B. BC2=AC·AB
C. AC= BC
D. BC= AC
D
课堂练习
2、上海东方明珠电视塔高468m,上球体是塔身的黄金分割点,它到塔底部的距离大约是多少米(精确到0.1m)?
468m
= 468×0.618
较长线段
全线段
=
较长线段
=
×全线段
468×
≈ 289.2
(m)
方法技巧:
课堂练习
3、已知线段 AB=6cm,点P为线段AB的黄金分割点,求线段AP的长.
解:
① 当 AP>BP 时,
AP=
较长线段
全线段
=
较长线段
=
×全线段
AB
=
(cm)
② 当 AP
AB
=
(cm)
较短线段=
全线段 -
较长线段
∴ AP=
AB-BP=
6-
=
(cm)
综上所述:
线段 AP的长为 cm 或 cm.
方法技巧:
=
=
×6
×6
课堂练习
5、【2018春 常熟市期末】如图,已知点C是线段AB的黄金分割点,且BC>AC.若S1表示以BC为边的正方形面积,S2表示长为AB、宽为AC的矩形面积,则S1与S2的大小关系为( )
4、演员报幕时应站在舞台的黄金分割处,若舞台长10米,则演员应站在距舞台一端 米远的地方.
A.S1>S2 B.S1=S2
C.S1<S2 D.不能确定
或
B
课堂练习
6、在人体躯干(脚底到肚脐的长度)与身高的比例上,肚脐是理想的黄金分割点,即比例越接近0.618,越给人以美感.张女士原来脚底到肚脐的长度与身高的比为0.60,她的身高为1.60m,她应该选择多高的高跟鞋穿上看起来更美?(精确到十分位)
解:
由题意可得,
下半身长是 160×0.6=96 (cm)
设选择的高跟鞋的高度是xcm.
96+x
160+x
=
即
96+x
160+x
=0.168
解得
x≈7.5
∴ 她应该选择7.5cm左右的高跟鞋穿上看起来更美.
根据黄金分割的定义,得
课堂练习
7、如图,在五角星形中,AD=BC,C,D两点都是AB的黄金分割点,AB=1,求CD的长.
解:
∵ C、D两点都是AB的黄金分割点
BD=
AB
=
∴ AC=
∴ AD=
AB-BD=
1-
∵ AD=BC
∴ AD=BC
∴ CD=
AB-AD-BC
=1-
课堂练习
8、如图所示,以长为2的定线段AB为边作正方形ABCD,取AB的中点P,连接PD,在BA的延长线上取点F,使PF=PD,以AF为边作正方形AMEF,点M在AD上.
(1) 求AM,DM的长;
(2) 点M是AD的黄金分割点吗?为什么?
2
1
课堂练习
黄金分割的应用
03
宽与长的比
巴台农神庙
(Parthenom Temple)
F
C
A
E
B
D
如果把图中用虚线表示的矩形画成如图所示的矩形ABCD,以矩形ABCD 的宽为边在其内部作正方形AEFD,那么我们可以惊奇地发现 , 点E是AB 的黄金分割点吗?矩形ABCD的宽与长的比是黄金比吗?为什么
BE
BC
=
BC
AB
这种矩形给人以美感.
等于黄金比的矩形
也称为黄金矩形.
概念学习:
黄金矩形
探究新知
练习:矩形的长和宽分别为 a 和 b,下列数据能构成黄金矩形的是( )
A. a=4,b=
B. a=4,b=
C. a=2,b=
D. a=2,b=
D
宽与长的比
等于黄金比的矩形
也称为黄金矩形.
探究新知
追溯历史文化
早在古希腊,数学家、天文学家欧多克索斯(Eudoxus,约前400——前347)曾提出:能否将一条线段分成不相等的两部分,使较短线段与较长线段的比等于较长线段与原线段的比?这就是黄金分割问题.
而发现黄金分割的是古希腊哲学家毕达哥拉斯。一天,毕达哥拉斯从一家铁匠铺路过,被铺子中那有节奏的叮叮当当的打铁声所吸引,便站在那里仔细聆听,似乎这声音中隐匿着什么秘密。他走进作坊,拿出一把尺量了一下铁锤和铁砧的尺寸,发现它们之间存在着一种十分和谐的关系。回到家里,毕达哥拉斯拿出一根线,想将它分为两段。怎样分才最好呢?经过反复比较,他最后确定0.618 :1的比例截断最优美。后来,意大利著名科学家、艺术家达·芬奇给这个比例冠以“黄金”二字的美名。
天文学家开普勒(Johannes Kepler,1571——1630)把这种分割线段的方法称为神圣分割,并指出,毕达哥拉斯定理(勾股定理)和黄金分割“是几何中的双宝,前者好比黄金,后者堪称珠玉”。 而历史上最早正式在书中使用“黄金分割”这个名称的是欧姆(Martin Ohm,1792——1872)。19世纪以后,“黄金分割”的说法逐渐流行起来… …
探究新知
人与黄金分割
人体肚脐不但是黄金点美化身型,有时还是医疗效果黄金点,许多民间名医在肚脐上贴药治好了某些疾病。人体最感舒适的温度是23℃(体温),也是正常人体温(37℃)的黄金点(23=37×0.618)。这说明医学与0.618有千丝万缕联系,尚待开拓研究。人体还有几个黄金点:肚脐上部分的黄金点在咽喉,肚脐以下部分的黄金点在膝盖,上肢的黄金点在肘关节。上肢与下肢长度之比均近似0.618.
探究新知
在人的面部,五官的分布越符合黄金分割,看起来就越美.
B
C
A
人与黄金分割
探究新知
绘画艺术中的黄金分割
著名画家达 芬奇的蒙娜丽莎构图就完美的体现了黄金分割在油画艺术上的应用。通过下面两幅图片可以看出来,蒙娜丽莎的头和两肩在整幅画面中都处于完美的体现了黄金分割,使得这幅油画看起来是那么的和谐和完美.
探究新知
雕塑--维纳斯
雕塑断臂女神维纳斯的体型完全与黄金比相符,即以人的肚脐为分界点,上身与下身之比,或者说下身与全身之比约是0.618 这样的身体给人的感觉就是非常的匀称,充满着美感.
建筑中的神秘数字
探究新知
建筑中的神秘数字
知道这是什么地方吗?
文明古国埃及的金字塔,形似方锥,大小各异。高(137米)与底边长(227米)之比为0.629,但这些金字塔底面的边长与高这比都接近于0.618.
探究新知
巴黎圣母院
联合国总部大厦
古希腊巴台农神庙
黄金分割,尤其宽与长的比为黄金比的矩形,在古典及现代建筑中都有广泛的应用.
建筑中的神秘数字
武器装备与黄金分割
当发射子弹的步枪刚刚制造出来的时候,它的枪把和枪身的长度比例很不科学合理,很不方便于抓握和瞄准。到了1918年,一个名叫阿尔文·约克的美远征军下士,对这种步枪进行了改造,改进后的枪型枪身和枪把的比例恰恰符合0.618的比例。
探究新知
黄金分割
点C把线段AB分成两条线段AC和BC,如果 , 那么称线段AB被点C黄金分割.点C叫做线段AB的黄金分割点,AC与AB的比称为黄金比.
黄金分割点:一条线段有两个黄金分割点
黄金比:较长线段:原线段 =
定义
课堂小结
感谢观看
