青岛版数学七年级上册 5.4.2用图象表示变量间的关系课件(共17张PPT)
文档属性
| 名称 | 青岛版数学七年级上册 5.4.2用图象表示变量间的关系课件(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 421.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-07 15:07:38 | ||
图片预览

文档简介
(共17张PPT)
第5章 代数式与函数的初步认识
5.4 生活中的常量与变量
第2课时 用图象表示变量间的关系
看图填空
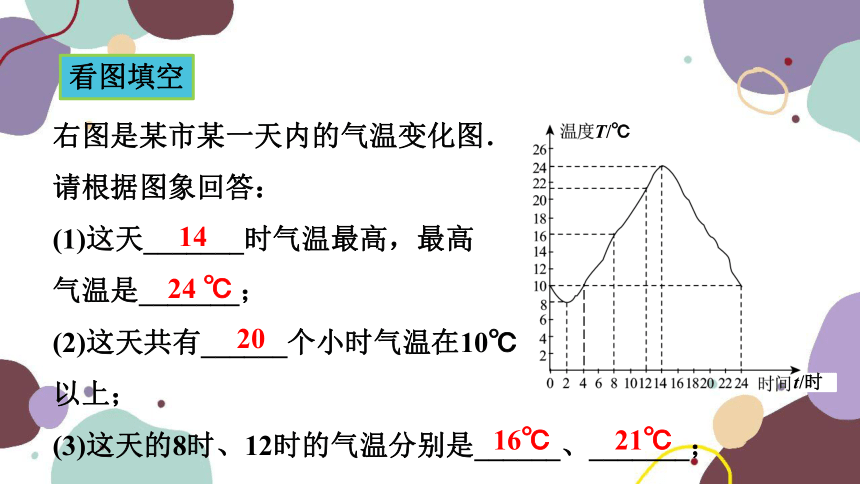
右图是某市某一天内的气温变化图.
请根据图象回答:
(1)这天_______时气温最高,最高
气温是_______;
(2)这天共有______个小时气温在10℃
以上;
(3)这天的8时、12时的气温分别是______、_______;
24 ℃
14
20
16℃
21℃
t/时
T/℃
方法探究
看图填空
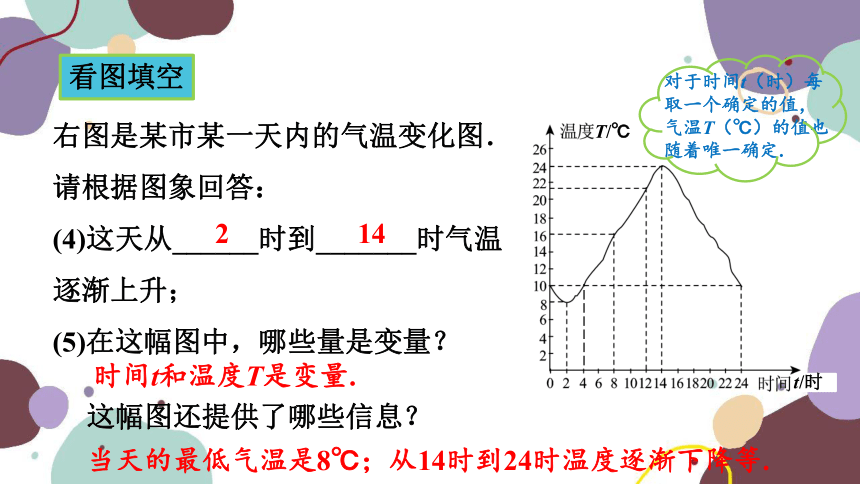
右图是某市某一天内的气温变化图.
请根据图象回答:
(4)这天从______时到_______时气温
逐渐上升;
(5)在这幅图中,哪些量是变量?
2
14
t/时
T/℃
时间t和温度T是变量.
这幅图还提供了哪些信息?
当天的最低气温是8℃;从14时到24时温度逐渐下降等.
对于时间t(时)每取一个确定的值,气温T(℃)的值也随着唯一确定.
新知学习
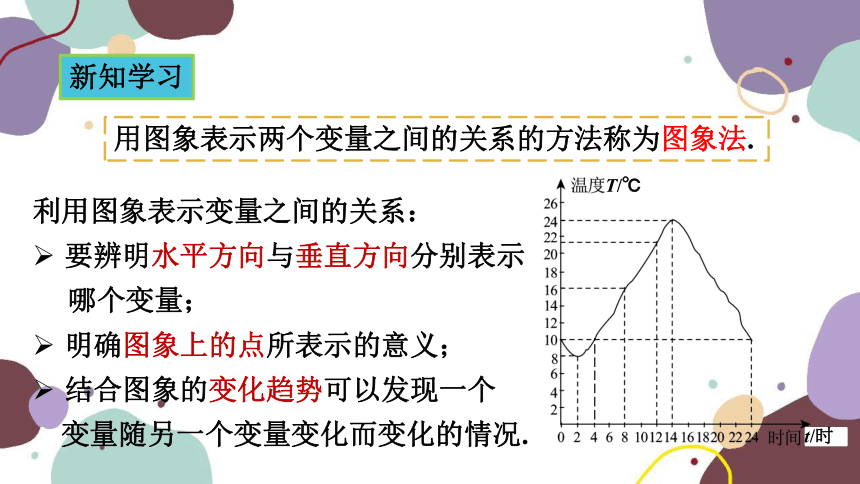
用图象表示两个变量之间的关系的方法称为图象法.
利用图象表示变量之间的关系:
要辨明水平方向与垂直方向分别表示
哪个变量;
明确图象上的点所表示的意义;
结合图象的变化趋势可以发现一个
变量随另一个变量变化而变化的情况.
t/时
T/℃
典例训练
0 5 10 15 20 25 30 35 40 45 50
20
15
10
5
呼吸作用强度
温度/℃
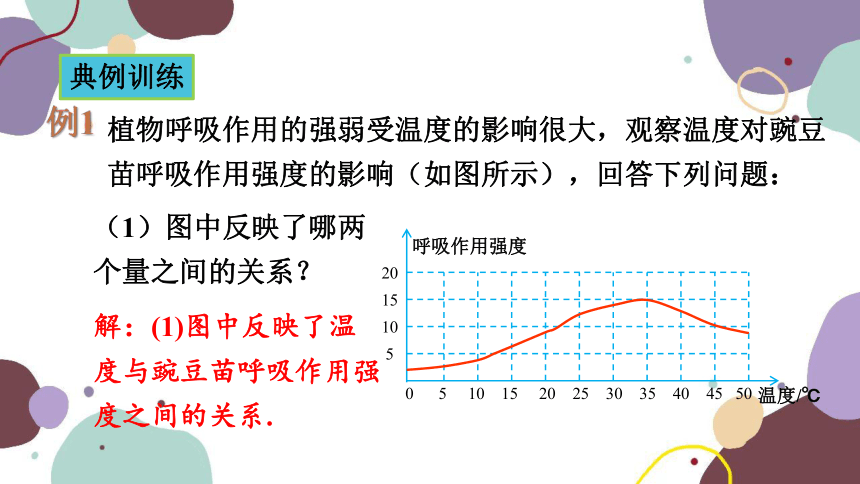
植物呼吸作用的强弱受温度的影响很大,观察温度对豌豆苗呼吸作用强度的影响(如图所示),回答下列问题:
(1)图中反映了哪两个量之间的关系?
例1
解:(1)图中反映了温
度与豌豆苗呼吸作用强度之间的关系.
典例训练
0 5 10 15 20 25 30 35 40 45 50
20
15
10
5
呼吸作用强度
温度/℃
植物呼吸作用的强弱受温度的影响很大,观察温度对豌豆苗呼吸作用强度的影响(如图所示),回答下列问题:
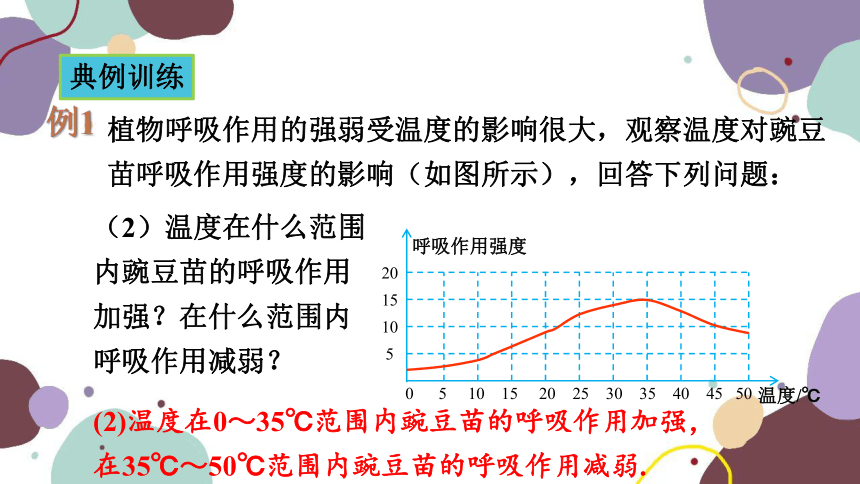
(2)温度在什么范围内豌豆苗的呼吸作用加强?在什么范围内呼吸作用减弱?
例1
(2)温度在0~35℃范围内豌豆苗的呼吸作用加强,在35℃~50℃范围内豌豆苗的呼吸作用减弱.
典例训练
0 5 10 15 20 25 30 35 40 45 50
20
15
10
5
呼吸作用强度
温度/℃
植物呼吸作用的强弱受温度的影响很大,观察温度对豌豆苗呼吸作用强度的影响(如图所示),回答下列问题:
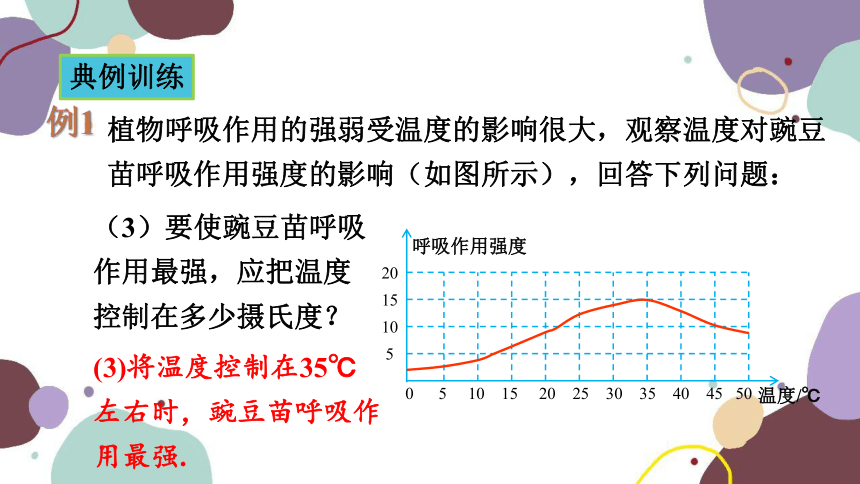
(3)要使豌豆苗呼吸作用最强,应把温度控制在多少摄氏度?
例1
(3)将温度控制在35℃左右时,豌豆苗呼吸作用最强.
典例训练
方法探究
看表答题
某地水库的蓄水量Q与最大水深h之间的关系,经过测量如下表所示:
最大水深h/米 0 5 10 15 20 25 30 35
蓄水量Q/万立方米 0 20 40 90 160 275 437.5 650
根据上表,回答下列问题:
(1)当最大水深为20米时,水库的蓄水量是多少?当最大水深为30米时,蓄水量是多少?
160万立方米.
437.5万立方米.
典例训练
方法探究
看表答题
某地水库的蓄水量Q与最大水深h之间的关系,经过测量如下表所示:
最大水深h/米 0 5 10 15 20 25 30 35
蓄水量Q/万立方米 0 20 40 90 160 275 437.5 650
根据上表,回答下列问题:
(2)在这个问题中,哪些量是变量?
最大水深h和蓄水量Q是变量.
最大水深h的值在表内第一行各值中选取,对于水深h每取一个确定的值,蓄水量Q的值也随之而唯一确定.
用表格表示两个变量之间的关系的方法称为列表法.
典例训练
商店出售一种瓜子,质量x(千克)与售价c(元)之间的关系如右表,表内售价栏中的0.1是塑料袋的价钱.
例2
质量x/千克 售价c/元
1 9+0.1
2 18+0.1
3 27+0.1
4 36+0.1
5 45+0.1
(1)表格中反映了哪两个变量之间的关系?
解:(1)表格中反映了
瓜子的质量x(千克)
与售价c(元)两个变
量之间的关系.
典例训练
商店出售一种瓜子,质量x(千克)与售价c(元)之间的关系如右表,表内售价栏中的0.1是塑料袋的价钱.
例2
质量x/千克 售价c/元
1 9+0.1
2 18+0.1
3 27+0.1
4 36+0.1
5 45+0.1
(2)写出售价c和质量x之间的关系式;
(2)c=9x+0.1
(3)当x=3.5时,
c的值是多少?
(3)当x=3.5时,c=9×3.5+0.1=31.6(元).
当堂检测
1.空中一个物体由静止自由下落,它下落的距离与时间之间有下面的关系:
时间t/秒 1 2 3 4 ···
距离h/米 4.9×1 4.9×4 4.9×9 4.9×16 ···
(1)当物体下落5秒时,它下落的距离是多少?
下落2.5秒时呢?
解:(1)物体下落5秒时的下落距离是4.9×25=122.5(米);
物体下落2.5秒时的下落距离是4.9×2.5 =30.625(米).
当堂检测
1.空中一个物体由静止自由下落,它下落的距离与时间之间有下面的关系:
时间t/秒 1 2 3 4 ···
距离h/米 4.9×1 4.9×4 4.9×9 4.9×16 ···
(2)将下落的距离h用关于时间t的代数式表示;
(2)下落的距离h用关于时间t的代数式表示为:h=4.9t .
(3)在这个问题中,哪些量是变量?哪些量是常量?
(3)变量是h,t,常量是4.9.
当堂检测
2.地球周围被厚厚的大气层包围,大气对物体会产生一定的压强.在不同的高度,由于空气稀薄程度不同,所产生的大气压也不同.如图表示的是不同海拔的大气压.
0 1 2 3 4 5 6 7 8 9 10 11 12 13
100
80
60
40
30
(1)海拔为2千米时,大气压约是多少?海拔为6.5千米时呢?
解:(1)80千帕;45千帕.
大气压/千帕
海拔/千米
当堂检测
2.地球周围被厚厚的大气层包围,大气对物体会产生一定的压强.在不同的高度,由于空气稀薄程度不同,所产生的大气压也不同.如图表示的是不同海拔的大气压.
0 1 2 3 4 5 6 7 8 9 10 11 12 13
100
80
60
40
30
(2)图中反映了哪两个量之间的关系?
(2)反映了海拔高度与大气压两个量之间的关系.
大气压/千帕
海拔/千米
当堂检测
2.地球周围被厚厚的大气层包围,大气对物体会产生一定的压强.在不同的高度,由于空气稀薄程度不同,所产生的大气压也不同.如图表示的是不同海拔的大气压.
0 1 2 3 4 5 6 7 8 9 10 11 12 13
100
80
60
40
30
(3)你从图中能得到什么信息?
(3)答案不唯一,如海拔高度为12千米时,大气压约为30千帕;海拔高度越高,大气压越低.
大气压/千帕
海拔/千米
归纳总结
1. 用图象表示两个变量之间的关系的方法称为图象法.
2. 用表格表示两个变量之间的关系的方法称为列表法.
用图象法表示两个变量之间的关系,读图时要分清水平数轴和垂直数轴分别表示的是哪个变量.
用列表法表示两个变量之间的关系,读表时要分清横行和纵列分别表示的意义.
第5章 代数式与函数的初步认识
5.4 生活中的常量与变量
第2课时 用图象表示变量间的关系
看图填空
右图是某市某一天内的气温变化图.
请根据图象回答:
(1)这天_______时气温最高,最高
气温是_______;
(2)这天共有______个小时气温在10℃
以上;
(3)这天的8时、12时的气温分别是______、_______;
24 ℃
14
20
16℃
21℃
t/时
T/℃
方法探究
看图填空
右图是某市某一天内的气温变化图.
请根据图象回答:
(4)这天从______时到_______时气温
逐渐上升;
(5)在这幅图中,哪些量是变量?
2
14
t/时
T/℃
时间t和温度T是变量.
这幅图还提供了哪些信息?
当天的最低气温是8℃;从14时到24时温度逐渐下降等.
对于时间t(时)每取一个确定的值,气温T(℃)的值也随着唯一确定.
新知学习
用图象表示两个变量之间的关系的方法称为图象法.
利用图象表示变量之间的关系:
要辨明水平方向与垂直方向分别表示
哪个变量;
明确图象上的点所表示的意义;
结合图象的变化趋势可以发现一个
变量随另一个变量变化而变化的情况.
t/时
T/℃
典例训练
0 5 10 15 20 25 30 35 40 45 50
20
15
10
5
呼吸作用强度
温度/℃
植物呼吸作用的强弱受温度的影响很大,观察温度对豌豆苗呼吸作用强度的影响(如图所示),回答下列问题:
(1)图中反映了哪两个量之间的关系?
例1
解:(1)图中反映了温
度与豌豆苗呼吸作用强度之间的关系.
典例训练
0 5 10 15 20 25 30 35 40 45 50
20
15
10
5
呼吸作用强度
温度/℃
植物呼吸作用的强弱受温度的影响很大,观察温度对豌豆苗呼吸作用强度的影响(如图所示),回答下列问题:
(2)温度在什么范围内豌豆苗的呼吸作用加强?在什么范围内呼吸作用减弱?
例1
(2)温度在0~35℃范围内豌豆苗的呼吸作用加强,在35℃~50℃范围内豌豆苗的呼吸作用减弱.
典例训练
0 5 10 15 20 25 30 35 40 45 50
20
15
10
5
呼吸作用强度
温度/℃
植物呼吸作用的强弱受温度的影响很大,观察温度对豌豆苗呼吸作用强度的影响(如图所示),回答下列问题:
(3)要使豌豆苗呼吸作用最强,应把温度控制在多少摄氏度?
例1
(3)将温度控制在35℃左右时,豌豆苗呼吸作用最强.
典例训练
方法探究
看表答题
某地水库的蓄水量Q与最大水深h之间的关系,经过测量如下表所示:
最大水深h/米 0 5 10 15 20 25 30 35
蓄水量Q/万立方米 0 20 40 90 160 275 437.5 650
根据上表,回答下列问题:
(1)当最大水深为20米时,水库的蓄水量是多少?当最大水深为30米时,蓄水量是多少?
160万立方米.
437.5万立方米.
典例训练
方法探究
看表答题
某地水库的蓄水量Q与最大水深h之间的关系,经过测量如下表所示:
最大水深h/米 0 5 10 15 20 25 30 35
蓄水量Q/万立方米 0 20 40 90 160 275 437.5 650
根据上表,回答下列问题:
(2)在这个问题中,哪些量是变量?
最大水深h和蓄水量Q是变量.
最大水深h的值在表内第一行各值中选取,对于水深h每取一个确定的值,蓄水量Q的值也随之而唯一确定.
用表格表示两个变量之间的关系的方法称为列表法.
典例训练
商店出售一种瓜子,质量x(千克)与售价c(元)之间的关系如右表,表内售价栏中的0.1是塑料袋的价钱.
例2
质量x/千克 售价c/元
1 9+0.1
2 18+0.1
3 27+0.1
4 36+0.1
5 45+0.1
(1)表格中反映了哪两个变量之间的关系?
解:(1)表格中反映了
瓜子的质量x(千克)
与售价c(元)两个变
量之间的关系.
典例训练
商店出售一种瓜子,质量x(千克)与售价c(元)之间的关系如右表,表内售价栏中的0.1是塑料袋的价钱.
例2
质量x/千克 售价c/元
1 9+0.1
2 18+0.1
3 27+0.1
4 36+0.1
5 45+0.1
(2)写出售价c和质量x之间的关系式;
(2)c=9x+0.1
(3)当x=3.5时,
c的值是多少?
(3)当x=3.5时,c=9×3.5+0.1=31.6(元).
当堂检测
1.空中一个物体由静止自由下落,它下落的距离与时间之间有下面的关系:
时间t/秒 1 2 3 4 ···
距离h/米 4.9×1 4.9×4 4.9×9 4.9×16 ···
(1)当物体下落5秒时,它下落的距离是多少?
下落2.5秒时呢?
解:(1)物体下落5秒时的下落距离是4.9×25=122.5(米);
物体下落2.5秒时的下落距离是4.9×2.5 =30.625(米).
当堂检测
1.空中一个物体由静止自由下落,它下落的距离与时间之间有下面的关系:
时间t/秒 1 2 3 4 ···
距离h/米 4.9×1 4.9×4 4.9×9 4.9×16 ···
(2)将下落的距离h用关于时间t的代数式表示;
(2)下落的距离h用关于时间t的代数式表示为:h=4.9t .
(3)在这个问题中,哪些量是变量?哪些量是常量?
(3)变量是h,t,常量是4.9.
当堂检测
2.地球周围被厚厚的大气层包围,大气对物体会产生一定的压强.在不同的高度,由于空气稀薄程度不同,所产生的大气压也不同.如图表示的是不同海拔的大气压.
0 1 2 3 4 5 6 7 8 9 10 11 12 13
100
80
60
40
30
(1)海拔为2千米时,大气压约是多少?海拔为6.5千米时呢?
解:(1)80千帕;45千帕.
大气压/千帕
海拔/千米
当堂检测
2.地球周围被厚厚的大气层包围,大气对物体会产生一定的压强.在不同的高度,由于空气稀薄程度不同,所产生的大气压也不同.如图表示的是不同海拔的大气压.
0 1 2 3 4 5 6 7 8 9 10 11 12 13
100
80
60
40
30
(2)图中反映了哪两个量之间的关系?
(2)反映了海拔高度与大气压两个量之间的关系.
大气压/千帕
海拔/千米
当堂检测
2.地球周围被厚厚的大气层包围,大气对物体会产生一定的压强.在不同的高度,由于空气稀薄程度不同,所产生的大气压也不同.如图表示的是不同海拔的大气压.
0 1 2 3 4 5 6 7 8 9 10 11 12 13
100
80
60
40
30
(3)你从图中能得到什么信息?
(3)答案不唯一,如海拔高度为12千米时,大气压约为30千帕;海拔高度越高,大气压越低.
大气压/千帕
海拔/千米
归纳总结
1. 用图象表示两个变量之间的关系的方法称为图象法.
2. 用表格表示两个变量之间的关系的方法称为列表法.
用图象法表示两个变量之间的关系,读图时要分清水平数轴和垂直数轴分别表示的是哪个变量.
用列表法表示两个变量之间的关系,读表时要分清横行和纵列分别表示的意义.
同课章节目录
- 第1章 基本的几何图形
- 1.1 我们身边的图形世界
- 1.2 几何图形
- 1.3 线段、射线和直线
- 1.4 线段的比较与作法
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数与绝对值
- 第3章 有理数的运算
- 3.1 有理数的加法与减法
- 3.2 有理数的乘法与除法
- 3.3 有理数的乘方
- 3.4 有理数的混合运算
- 3.5 利用计算器进行有理数的计算
- 第4章 数据的收集整理与描述
- 4.1 普查和抽样调查
- 4.2 简单随机抽样
- 4.3 数据的整理
- 4.4 扇形统计图
- 第5章 代数式与函数的初步认识
- 5.1 用字母表示数
- 5.2 代数式
- 5.3 代数式的值
- 5.4 生活中的常量与变量
- 5.5 函数的初步认识
- 第6章 整式的加减
- 6.1 单项式与多项式
- 6.2 同类项
- 6.3 去括号
- 6.4 整式的加减
- 第7章 一元一次方程
- 7.1 等式的基本性质
- 7.2 一元一次方程
- 7.3 一元一次方程的解法
- 7.4 一元一次方程的应用
