华师版数学七年级上册 5.2 第1课时 平行线 课件(共15张PPT)
文档属性
| 名称 | 华师版数学七年级上册 5.2 第1课时 平行线 课件(共15张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 359.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-07 14:36:58 | ||
图片预览






文档简介
(共15张PPT)
第5章 相交线与平行线
5.2 平行线
第1课时 平行线
a
b
在同一平面内不相交的两条直线叫做平行线.
如右图所示,直线a与直线b相互平行,
记作“a//b”.
在同一平面内,两条不重合的直线的位置关系只有两种:
相交或平行.
平行线的定义
一
例1 判断下列说法是否正确,并说明理由.
(1)不相交的两条直线是平行线;
(2)在同一平面内,两条不相交的线段是平行线.
解:(1)不正确;
理由:根据定义,它缺少了“在同一平面内” 这一条件.
(2)不正确;
理由:定义中指出的是两条不相交的“直线”, 而不是“线段”.
例题讲解
平行线的画法
二
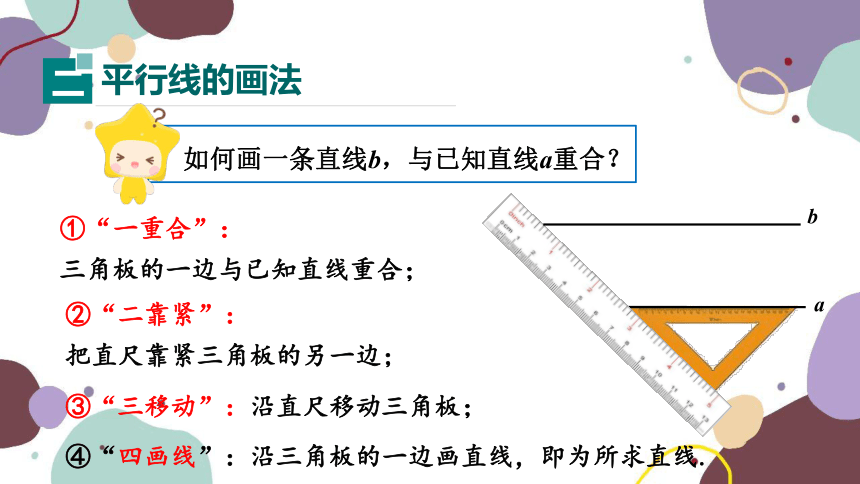
如何画一条直线b,与已知直线a重合?
b
a
①“一重合”:
三角板的一边与已知直线重合;
②“二靠紧”:
把直尺靠紧三角板的另一边;
③“三移动”:沿直尺移动三角板;
④“四画线”:沿三角板的一边画直线,即为所求直线.
如图所示,不少国家的国旗、团体或公司的标志的图案是由平行线、垂线构成的.
小组合作,再举出一些例子.
平行线基本事实及其推论
三
做一做:
如果在直线a外有一个已知点P,那么经过点P可以画多少条
直线与已知直线a平行?小组合作,请动手画一画.
a
b
P
动手操作结果表明,经过点P只能画一条直线与已知直线a平行.
平行线的基本事实:
过直线外一点有且只有一条直线与这条直线平行.
试一试:
画一条直线a,按如图所示的方法,画一条直线b与直线a平行,再向上推三角尺,画另一条直线c,也与直线a平行.
你发现直线b与直线c有什么关系?你的同伴是否也有类似发现?
a
c
b
发现:直线b与直线c平行.
推论:如果两条直线都和第三条直线平行,那么这两条直线也互相平行.
例题讲解
例2 如图所示,点O为直线AB外的一点,用直尺和三角尺过点O画直线CD//AB.
小组合作,用三角尺和直尺解决问题,之后对照答案看解答是否准确.
【答案】画法:(1)把三角尺的一边放在已知直线AB上;
(2)把直尺紧靠在三角尺的另一边上;
(3)把三角尺沿着直尺的边推到刚好落在已知点O的位置;
(4)沿三角尺经过点O的边画直线CD.
CD即为所求.
C
D
例3 下列说法中正确的个数是( )
①经过直线外一点,有且只有一条直线与已知直线相交;
②过一点有且只有一条直线和已知直线平行;
③若直线a//b,b//c,则a//c.
A.0 B.1 C.2 D.3
解析:经过直线外一点,可以画无数条直线与已知直线相交,所以①错误;过已知直线上的一点不可能画一条直线和这条直线平行,所以②错误,应修改为过直线外一点有且只有一条直线与这条直线平行;③是平行线的传递性,正确.
B
随堂练习
1.下列说法中不正确的个数为( )
①在同一平面内,不重合的两条直线的位置关系只有平行与相交两种;②在同一平面内,不相交的两条线段互相平行;③不相交的两条直线是平行线;④在同一平面内,不相交的两条射线互相平行.
A.4 B.3 C.2 D.1
解析:①正确;两条线段或两条射线平行,是指它们所在的直线平行,两条线段或射线不相交,不能保证它们所在直线不相交,②与④错误;平行线的前提是在同一平面内,所以③错误.
B
2.a,b,c是平面内任意三条直线,交点可以有( )
A.1个或2个或3个
B.0个或1个或2个或3个
C.1个或2个
D.以上都不对
B
解析:
没有交点
一个交点
两个交点
三个交点
3.已知∠AOB,P是任意一点,若过点P画一条直线与OA平行,那么这样的直线( )
A.有且只有一条
B.有两条
C.不存在
D.有一条或不存在
解析:当点P在OA所在直线外的时候,有一条,
如果点P在OA上,则不存在,故选D.
D
4.观察如图所示的长方体后填空:
(1)用符号表示下列两棱位置关系:
A1B1_____AB,AA1_____AB,
A1D1____C1D1,AD_____BC;
(2)A1B1与BC所在的直线是两条不相交的直线,
它们______平行线(填“是”或“不是”),由此可知,
在______________,两条不相交的直线才能叫做平行线.
A
B
C
D
A1
B1
C1
D1
//
⊥
⊥
//
不是
同一个平面内
课堂小结
平行线的定义包含缺一不可的三个条件:
①在同一平面内;②不相交;③都是直线.
一放、二靠、三移、四画
1.平行线的定义及平面内两直线的位置关系
2.平行线的画法
(1)“有且只有”强调直线的存在性和唯一性;
(2)前提条件“经过直线外一点”,若点在直线上,不可能有平行线.
3.平行线的基本事实及推论
课堂小结
第5章 相交线与平行线
5.2 平行线
第1课时 平行线
a
b
在同一平面内不相交的两条直线叫做平行线.
如右图所示,直线a与直线b相互平行,
记作“a//b”.
在同一平面内,两条不重合的直线的位置关系只有两种:
相交或平行.
平行线的定义
一
例1 判断下列说法是否正确,并说明理由.
(1)不相交的两条直线是平行线;
(2)在同一平面内,两条不相交的线段是平行线.
解:(1)不正确;
理由:根据定义,它缺少了“在同一平面内” 这一条件.
(2)不正确;
理由:定义中指出的是两条不相交的“直线”, 而不是“线段”.
例题讲解
平行线的画法
二
如何画一条直线b,与已知直线a重合?
b
a
①“一重合”:
三角板的一边与已知直线重合;
②“二靠紧”:
把直尺靠紧三角板的另一边;
③“三移动”:沿直尺移动三角板;
④“四画线”:沿三角板的一边画直线,即为所求直线.
如图所示,不少国家的国旗、团体或公司的标志的图案是由平行线、垂线构成的.
小组合作,再举出一些例子.
平行线基本事实及其推论
三
做一做:
如果在直线a外有一个已知点P,那么经过点P可以画多少条
直线与已知直线a平行?小组合作,请动手画一画.
a
b
P
动手操作结果表明,经过点P只能画一条直线与已知直线a平行.
平行线的基本事实:
过直线外一点有且只有一条直线与这条直线平行.
试一试:
画一条直线a,按如图所示的方法,画一条直线b与直线a平行,再向上推三角尺,画另一条直线c,也与直线a平行.
你发现直线b与直线c有什么关系?你的同伴是否也有类似发现?
a
c
b
发现:直线b与直线c平行.
推论:如果两条直线都和第三条直线平行,那么这两条直线也互相平行.
例题讲解
例2 如图所示,点O为直线AB外的一点,用直尺和三角尺过点O画直线CD//AB.
小组合作,用三角尺和直尺解决问题,之后对照答案看解答是否准确.
【答案】画法:(1)把三角尺的一边放在已知直线AB上;
(2)把直尺紧靠在三角尺的另一边上;
(3)把三角尺沿着直尺的边推到刚好落在已知点O的位置;
(4)沿三角尺经过点O的边画直线CD.
CD即为所求.
C
D
例3 下列说法中正确的个数是( )
①经过直线外一点,有且只有一条直线与已知直线相交;
②过一点有且只有一条直线和已知直线平行;
③若直线a//b,b//c,则a//c.
A.0 B.1 C.2 D.3
解析:经过直线外一点,可以画无数条直线与已知直线相交,所以①错误;过已知直线上的一点不可能画一条直线和这条直线平行,所以②错误,应修改为过直线外一点有且只有一条直线与这条直线平行;③是平行线的传递性,正确.
B
随堂练习
1.下列说法中不正确的个数为( )
①在同一平面内,不重合的两条直线的位置关系只有平行与相交两种;②在同一平面内,不相交的两条线段互相平行;③不相交的两条直线是平行线;④在同一平面内,不相交的两条射线互相平行.
A.4 B.3 C.2 D.1
解析:①正确;两条线段或两条射线平行,是指它们所在的直线平行,两条线段或射线不相交,不能保证它们所在直线不相交,②与④错误;平行线的前提是在同一平面内,所以③错误.
B
2.a,b,c是平面内任意三条直线,交点可以有( )
A.1个或2个或3个
B.0个或1个或2个或3个
C.1个或2个
D.以上都不对
B
解析:
没有交点
一个交点
两个交点
三个交点
3.已知∠AOB,P是任意一点,若过点P画一条直线与OA平行,那么这样的直线( )
A.有且只有一条
B.有两条
C.不存在
D.有一条或不存在
解析:当点P在OA所在直线外的时候,有一条,
如果点P在OA上,则不存在,故选D.
D
4.观察如图所示的长方体后填空:
(1)用符号表示下列两棱位置关系:
A1B1_____AB,AA1_____AB,
A1D1____C1D1,AD_____BC;
(2)A1B1与BC所在的直线是两条不相交的直线,
它们______平行线(填“是”或“不是”),由此可知,
在______________,两条不相交的直线才能叫做平行线.
A
B
C
D
A1
B1
C1
D1
//
⊥
⊥
//
不是
同一个平面内
课堂小结
平行线的定义包含缺一不可的三个条件:
①在同一平面内;②不相交;③都是直线.
一放、二靠、三移、四画
1.平行线的定义及平面内两直线的位置关系
2.平行线的画法
(1)“有且只有”强调直线的存在性和唯一性;
(2)前提条件“经过直线外一点”,若点在直线上,不可能有平行线.
3.平行线的基本事实及推论
课堂小结
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
