第5章 相交线和平行线复习自测卷(含答案 )
文档属性
| 名称 | 第5章 相交线和平行线复习自测卷(含答案 ) |  | |
| 格式 | doc | ||
| 文件大小 | 300.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-06 21:35:43 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第5章 相交线和平行线复习自测
一、选择题:本大题共12小题,每小题4分,共48分. 在每个小题给出的四个选项中,只有一项是符合题目要求的.
1.已知∠1和∠2是对顶角,∠1=180°∠θ,∠2=43°,则∠θ=( )
A.32° B.57° C.105° D.137°
2.如图,∠1的内错角是( )
A.∠2 B.∠3 C.∠4 D.∠5
3.下列说法错误的是( )
A.同一平面内无公共点的两直线必平行
B.同一平面内,垂直于同一条直线的两直线平行
C.两直线平行,同旁内角相等
D.同位角相等,两直线平行
4.下图中,直线PQ与射线AB或线段MN能相交的是( )
A. B. C. D.
5.如图,已知直线a∥b,∠1=123°,则∠2+∠3 =( )
A.246° B.180°
C.114° D.57°
6.如果∠α与∠β是对顶角且互补,则它们的角的两边所在的直线( )
A.互相垂直 B.互相 平行 C.相交但不垂直 D.位置不确定
7.若一个角的余角是62°,则这个角的补角是( )
A.28° B.36° C.118° D.152°
8.如图,过直线a外一点P作PA⊥a 于点A,在直线a上取一点B,连结PB使 PB=2PA ,点C在线段AB上,连结PC.若PA=3.5 ,则线段PC的长可能是( )
A.3.2 B.4.9
C.7.3 D.8.1
9.如图,AD∥BC,点E在BD的延长线上,若∠ADE=145°,
则∠DBC的度数为( )
A.15° B.35°
C.45° D.65°
10.如图,已知AB∥CD,∠DFE=115°,则∠ABE的度数为( )
A.30° B.45°
C.65° D.90°
11.点M、N分别在∠AOB的边OA、OB上,点M到OB的垂线段为ME,点N到OA的垂线段为NF,下图中正确的图形是( )
A. B. C. D.
12.如图,若∠3=∠4,则下列条件中,不能判定AB∥CD的是( )
A.∠1+∠2=90° B.∠1=∠3且∠2=∠4
C.∠1+∠3=90°且∠2+∠4=90° D.∠1=∠2
二、填空题:本大题共6小题,每小题4分,共24分.
13.如图,AD∥BC,∠B=65°,∠α=∠C,则∠C= .
14.已知∠1与∠2互余,∠1=(2x+15)°,∠2=(3x30)°,则x= °.
15.如图,∠1=105°,∠2=75°,∠3=89°,则∠4= .
16.若∠α的余角和∠α的补角的度数之比是3∶8,则∠α= .
17.同一平面内,∠A与∠B的两边互相垂直,∠B比∠A的2倍少30°,则∠A= .
18.同一平面内,2条直线相交只有一个交点,3条直线两两相交最多能有3个交点,4条直线两两相交最多能有6个交点,5条直线两两相交最多能有10个交点,9条直线两两相交最多能有______个交点.
三、解答题:本题共78分,解答应写出文字说明、证明过程或计算步骤.
19.(本小题满分16分)填空或填写理由.
(1)如图甲:∵∠ =∠ (已知);
∴AB∥CD( , )
(2)如图乙:已知直线a∥b,∠2=80°,求∠1,∠3的度数.
解:∵a∥b, (已知)
∴∠1=∠4( , )
又∵∠4=∠2( )
∠2=80°(已知)
∴∠1=( )(等量代换)
又∵∠2+∠3=180°
∴∠3=( )(等式的性质)
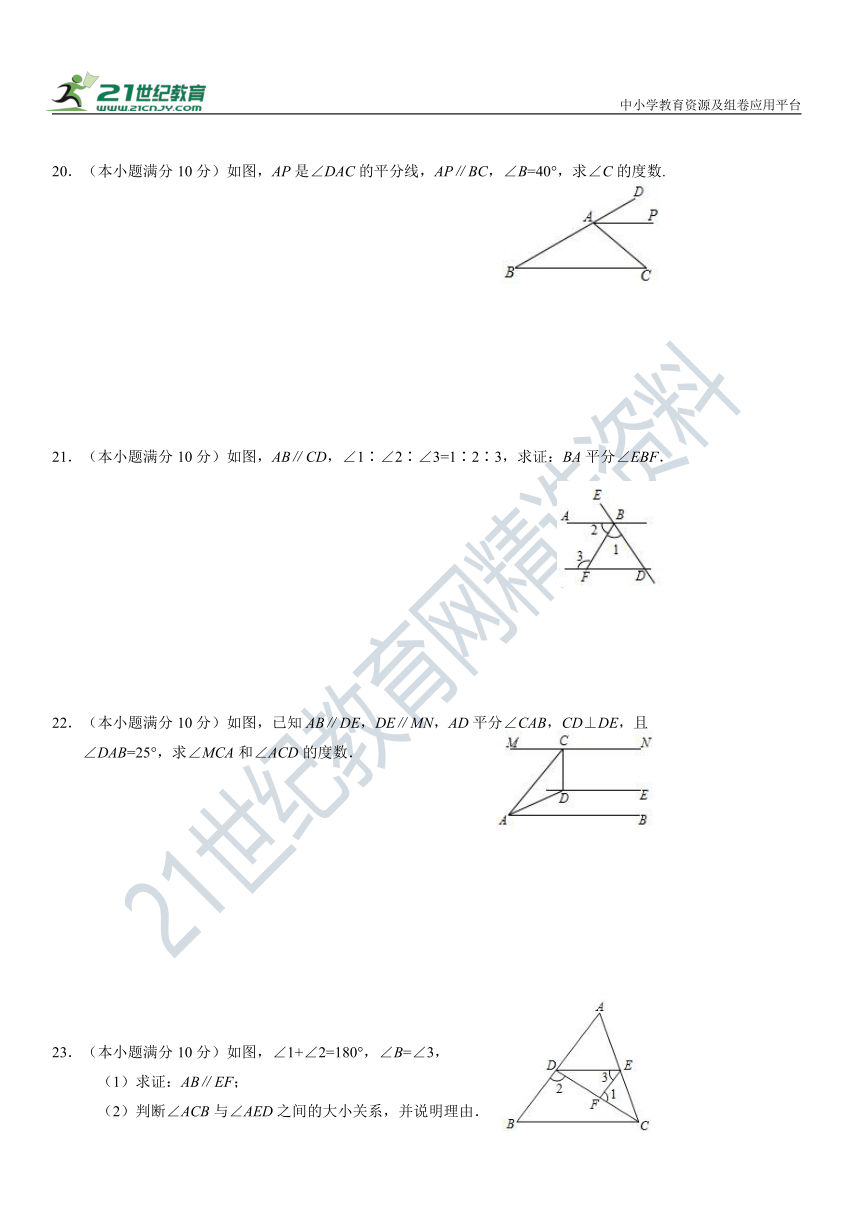
20.(本小题满分10分)如图,AP是∠DAC的平分线,AP∥BC,∠B=40°,求∠C的度数.
21.(本小题满分10分)如图,AB∥CD,∠1∶∠2∶∠3=1∶2∶3,求证:BA平分∠EBF.
22.(本小题满分10分)如图,已知AB∥DE,DE∥MN,AD平分∠CAB,CD⊥DE,且
∠DAB=25°,求∠MCA和∠ACD的度数.
23.(本小题满分10分)如图,∠1+∠2=180°,∠B=∠3,
(1)求证:AB∥EF;
(2)判断∠ACB与∠AED之间的大小关系,并说明理由.
24.(本小题满分10分)如图,AB∥CD,∠1=∠2,∠FDE=80°,∠3=50°,∠B=70°.
(1)求∠2的度数;
(2)CE与AF平行吗?为什么?
(3)求∠BCE的度数.
注:在(1)、(2)的解答、推理过程中填空,并模仿解答、推理过程完成问题(3)
解:(1)∵∠1+∠2+∠FDE=180°( )
∵∠FDE=80°(已知),∠1=∠2(已知)
∴2∠2+80°=180° ( )
∠2=90°40° ( )
= °.
(2)CE与AF ( ).
∵∠3= °(已知)
∵∠1=∠2(已知),∠2= °
∴∠1=∠3( )
∴ ( )
(3)模仿上面的解答、推理过程完成该小题.
25.(本小题满分12分)已知AB∥CD,点O不在直线AB、CD上,且AO⊥OC于点O.
(1)如图1,求∠A和∠C之间的数量关系;
(2)如图2,过点O作OE⊥AB于点E,
求证:∠AOE=∠C;
(3)如图3,在(2)的条件下,点F、
G在线段BE上,OF平分∠AOE,OG平
分∠COE,若∠GCD+∠GOC=180°,试判
断∠OGC与∠EOF之间的数量关系,并说明理由.
参考答案
一、 选择题
1.D 2.A 3.C 4.D 5.C 6.A 7.D 8.B 9.B 10.C 11.C 12.A
二、填空题
13.65° 14.21° 15.89° 16.36° 17.30°或70° 18.36
三.解答题
19.解:(1)∵∠1=∠4(已知);
∴AB∥CD(内错角相等,两直线平行)
故答案为:1,4,内错角相等,两直线平行;
(2)∵a∥b,(已知)
∴∠1=∠4(两直线平行,同位角相等)
又∵∠4=∠2(对顶角相等)
∴∠2=80°(已知)
∴∠1=80°(等量代换)
又∵∠2+∠3=180°
∴∠3=100°(等式的性质).
20.解:∵AD∥BC,∠B=40°,
∴∠PAD=∠B=40°,
∵AD是∠EAC的平分线,
∴∠PAD=∠PAC=40°,
∵AD∥BC,
∴∠C=∠PAC,∴∠C=40°
21.证明:设∠1=x,则∠2=2x,∠3=3x,
∵AB∥CD,
∴∠2+∠3=180°,即2x+3x=180°,解得x=36°,
∴∠1=36°,∠2=72°,
∴∠EBA=180°∠2∠1=180°72°36°=72°,
∴∠EBA=∠2,∴BA平分∠EBF.
22.解:(1)∵AB∥DE,DE∥MN,∴AB∥MN,
∵AD平分∠CAB,∠DAB=25°,
∴∠CAB=2∠DAB=50°,
∵MN∥AB,∴∠MCA=∠CAB=50°,
(2)∵CD⊥DE,∴∠CDE=90°,
∵MN∥DE,∴∠MCD=∠CDE=90°,
∴∠ACD=∠MCD-∠MCA=90°-50°=40°;
23.证明:(1)∵∠1+∠2=180,∠1+∠EFD=180°,
∴∠2=∠EFD,∴AB∥EF;
(2)解:∠ACB=∠AED,
理由是:∵EF∥AB,∴∠3=∠ADE,
∵∠B=∠3,∴∠B=∠ADE,
∴DE∥BC,∴∠ACB=∠AED
24.解:(1)∵∠1+∠2+∠FDE=180°(平角等于180°),
∵∠FDE=80°(已知),∵∠1=∠2(已知),
∴2∠2+80°=180° (等量替换),
∠2=90°40°(等式两边同时除以2),
=50°.
(2)CE与AF (互相平行).
∵∠3= 50 °(已知)
∵∠1=∠2(已知),∠2= 50 °
∴∠1=∠3( 等量代换 )
∴ CE∥AF( 内错角相等,两直线平行 )
(3)∵AB∥CD(已知),
∴∠B+∠BCD=180°(两直线平行,同旁内角互补).
∵∠B=70°(已知),
∴∠BCD=180°∠B=110°,
∴∠BCE=∠BCD+∠3=160°.
25.解:(1)如图1中,
∵AB∥CD,∴∠1=∠C,
∵AO⊥OC,∴∠A+∠1=90°,
∴∠A+∠C=90°,故答案为∠A+∠C=90°.
(2)证明:如图2中,
∵AB∥CD ∴∠OAE+∠C=∠AOC=90°,
∵OE⊥AB, ∴∠AEO=90°,
∴∠OAE+∠C=∠AEO,
∴∠AOE+∠C=∠AEO,
∵∠AOE+∠OAE=90°, ∴∠AOE=∠C.
(3)解:结论:∠OGC=2∠EOF.
理由:如图3中,设∠EOF=∠AOF=y,∠COG=∠GOE=x.
∵AB∥CD,∴∠DCG+∠CGA=180°,
∵∠DCG+∠GOC=180°,∴∠EGC=∠GOC=x,
∵OE⊥AB,OA⊥OC,∴∠E=∠AOC=90°,
∴∠OGC=∠CGE∠EGC=x[90°2y(90°x)]=2y,
∴∠OGC=2∠EOF.
(2题图)
(12题图)
(13题图)
(15题图)
图甲
图乙
第5章 相交线和平行线复习自测
一、选择题:本大题共12小题,每小题4分,共48分. 在每个小题给出的四个选项中,只有一项是符合题目要求的.
1.已知∠1和∠2是对顶角,∠1=180°∠θ,∠2=43°,则∠θ=( )
A.32° B.57° C.105° D.137°
2.如图,∠1的内错角是( )
A.∠2 B.∠3 C.∠4 D.∠5
3.下列说法错误的是( )
A.同一平面内无公共点的两直线必平行
B.同一平面内,垂直于同一条直线的两直线平行
C.两直线平行,同旁内角相等
D.同位角相等,两直线平行
4.下图中,直线PQ与射线AB或线段MN能相交的是( )
A. B. C. D.
5.如图,已知直线a∥b,∠1=123°,则∠2+∠3 =( )
A.246° B.180°
C.114° D.57°
6.如果∠α与∠β是对顶角且互补,则它们的角的两边所在的直线( )
A.互相垂直 B.互相 平行 C.相交但不垂直 D.位置不确定
7.若一个角的余角是62°,则这个角的补角是( )
A.28° B.36° C.118° D.152°
8.如图,过直线a外一点P作PA⊥a 于点A,在直线a上取一点B,连结PB使 PB=2PA ,点C在线段AB上,连结PC.若PA=3.5 ,则线段PC的长可能是( )
A.3.2 B.4.9
C.7.3 D.8.1
9.如图,AD∥BC,点E在BD的延长线上,若∠ADE=145°,
则∠DBC的度数为( )
A.15° B.35°
C.45° D.65°
10.如图,已知AB∥CD,∠DFE=115°,则∠ABE的度数为( )
A.30° B.45°
C.65° D.90°
11.点M、N分别在∠AOB的边OA、OB上,点M到OB的垂线段为ME,点N到OA的垂线段为NF,下图中正确的图形是( )
A. B. C. D.
12.如图,若∠3=∠4,则下列条件中,不能判定AB∥CD的是( )
A.∠1+∠2=90° B.∠1=∠3且∠2=∠4
C.∠1+∠3=90°且∠2+∠4=90° D.∠1=∠2
二、填空题:本大题共6小题,每小题4分,共24分.
13.如图,AD∥BC,∠B=65°,∠α=∠C,则∠C= .
14.已知∠1与∠2互余,∠1=(2x+15)°,∠2=(3x30)°,则x= °.
15.如图,∠1=105°,∠2=75°,∠3=89°,则∠4= .
16.若∠α的余角和∠α的补角的度数之比是3∶8,则∠α= .
17.同一平面内,∠A与∠B的两边互相垂直,∠B比∠A的2倍少30°,则∠A= .
18.同一平面内,2条直线相交只有一个交点,3条直线两两相交最多能有3个交点,4条直线两两相交最多能有6个交点,5条直线两两相交最多能有10个交点,9条直线两两相交最多能有______个交点.
三、解答题:本题共78分,解答应写出文字说明、证明过程或计算步骤.
19.(本小题满分16分)填空或填写理由.
(1)如图甲:∵∠ =∠ (已知);
∴AB∥CD( , )
(2)如图乙:已知直线a∥b,∠2=80°,求∠1,∠3的度数.
解:∵a∥b, (已知)
∴∠1=∠4( , )
又∵∠4=∠2( )
∠2=80°(已知)
∴∠1=( )(等量代换)
又∵∠2+∠3=180°
∴∠3=( )(等式的性质)
20.(本小题满分10分)如图,AP是∠DAC的平分线,AP∥BC,∠B=40°,求∠C的度数.
21.(本小题满分10分)如图,AB∥CD,∠1∶∠2∶∠3=1∶2∶3,求证:BA平分∠EBF.
22.(本小题满分10分)如图,已知AB∥DE,DE∥MN,AD平分∠CAB,CD⊥DE,且
∠DAB=25°,求∠MCA和∠ACD的度数.
23.(本小题满分10分)如图,∠1+∠2=180°,∠B=∠3,
(1)求证:AB∥EF;
(2)判断∠ACB与∠AED之间的大小关系,并说明理由.
24.(本小题满分10分)如图,AB∥CD,∠1=∠2,∠FDE=80°,∠3=50°,∠B=70°.
(1)求∠2的度数;
(2)CE与AF平行吗?为什么?
(3)求∠BCE的度数.
注:在(1)、(2)的解答、推理过程中填空,并模仿解答、推理过程完成问题(3)
解:(1)∵∠1+∠2+∠FDE=180°( )
∵∠FDE=80°(已知),∠1=∠2(已知)
∴2∠2+80°=180° ( )
∠2=90°40° ( )
= °.
(2)CE与AF ( ).
∵∠3= °(已知)
∵∠1=∠2(已知),∠2= °
∴∠1=∠3( )
∴ ( )
(3)模仿上面的解答、推理过程完成该小题.
25.(本小题满分12分)已知AB∥CD,点O不在直线AB、CD上,且AO⊥OC于点O.
(1)如图1,求∠A和∠C之间的数量关系;
(2)如图2,过点O作OE⊥AB于点E,
求证:∠AOE=∠C;
(3)如图3,在(2)的条件下,点F、
G在线段BE上,OF平分∠AOE,OG平
分∠COE,若∠GCD+∠GOC=180°,试判
断∠OGC与∠EOF之间的数量关系,并说明理由.
参考答案
一、 选择题
1.D 2.A 3.C 4.D 5.C 6.A 7.D 8.B 9.B 10.C 11.C 12.A
二、填空题
13.65° 14.21° 15.89° 16.36° 17.30°或70° 18.36
三.解答题
19.解:(1)∵∠1=∠4(已知);
∴AB∥CD(内错角相等,两直线平行)
故答案为:1,4,内错角相等,两直线平行;
(2)∵a∥b,(已知)
∴∠1=∠4(两直线平行,同位角相等)
又∵∠4=∠2(对顶角相等)
∴∠2=80°(已知)
∴∠1=80°(等量代换)
又∵∠2+∠3=180°
∴∠3=100°(等式的性质).
20.解:∵AD∥BC,∠B=40°,
∴∠PAD=∠B=40°,
∵AD是∠EAC的平分线,
∴∠PAD=∠PAC=40°,
∵AD∥BC,
∴∠C=∠PAC,∴∠C=40°
21.证明:设∠1=x,则∠2=2x,∠3=3x,
∵AB∥CD,
∴∠2+∠3=180°,即2x+3x=180°,解得x=36°,
∴∠1=36°,∠2=72°,
∴∠EBA=180°∠2∠1=180°72°36°=72°,
∴∠EBA=∠2,∴BA平分∠EBF.
22.解:(1)∵AB∥DE,DE∥MN,∴AB∥MN,
∵AD平分∠CAB,∠DAB=25°,
∴∠CAB=2∠DAB=50°,
∵MN∥AB,∴∠MCA=∠CAB=50°,
(2)∵CD⊥DE,∴∠CDE=90°,
∵MN∥DE,∴∠MCD=∠CDE=90°,
∴∠ACD=∠MCD-∠MCA=90°-50°=40°;
23.证明:(1)∵∠1+∠2=180,∠1+∠EFD=180°,
∴∠2=∠EFD,∴AB∥EF;
(2)解:∠ACB=∠AED,
理由是:∵EF∥AB,∴∠3=∠ADE,
∵∠B=∠3,∴∠B=∠ADE,
∴DE∥BC,∴∠ACB=∠AED
24.解:(1)∵∠1+∠2+∠FDE=180°(平角等于180°),
∵∠FDE=80°(已知),∵∠1=∠2(已知),
∴2∠2+80°=180° (等量替换),
∠2=90°40°(等式两边同时除以2),
=50°.
(2)CE与AF (互相平行).
∵∠3= 50 °(已知)
∵∠1=∠2(已知),∠2= 50 °
∴∠1=∠3( 等量代换 )
∴ CE∥AF( 内错角相等,两直线平行 )
(3)∵AB∥CD(已知),
∴∠B+∠BCD=180°(两直线平行,同旁内角互补).
∵∠B=70°(已知),
∴∠BCD=180°∠B=110°,
∴∠BCE=∠BCD+∠3=160°.
25.解:(1)如图1中,
∵AB∥CD,∴∠1=∠C,
∵AO⊥OC,∴∠A+∠1=90°,
∴∠A+∠C=90°,故答案为∠A+∠C=90°.
(2)证明:如图2中,
∵AB∥CD ∴∠OAE+∠C=∠AOC=90°,
∵OE⊥AB, ∴∠AEO=90°,
∴∠OAE+∠C=∠AEO,
∴∠AOE+∠C=∠AEO,
∵∠AOE+∠OAE=90°, ∴∠AOE=∠C.
(3)解:结论:∠OGC=2∠EOF.
理由:如图3中,设∠EOF=∠AOF=y,∠COG=∠GOE=x.
∵AB∥CD,∴∠DCG+∠CGA=180°,
∵∠DCG+∠GOC=180°,∴∠EGC=∠GOC=x,
∵OE⊥AB,OA⊥OC,∴∠E=∠AOC=90°,
∴∠OGC=∠CGE∠EGC=x[90°2y(90°x)]=2y,
∴∠OGC=2∠EOF.
(2题图)
(12题图)
(13题图)
(15题图)
图甲
图乙
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
