2022-2023学年人教版八年级数学下册《第20章数据的分析》题型分类练习题(含解析)
文档属性
| 名称 | 2022-2023学年人教版八年级数学下册《第20章数据的分析》题型分类练习题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 90.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-07 15:17:05 | ||
图片预览




文档简介
2022-2023学年人教版八年级数学下册《第20章数据的分析》题型分类练习题(附答案)
一.易错题
1.某同学使用计算器求30个数据的平均数时,错将其中的一个数据105输入为15,那么由此求出的平均数与实际平均数的差是( )
A.﹣3.5 B.3 C.0.5 D.﹣3
2.甲、乙、丙三种糖果售价分别为每千克6元,7元,8元,若将甲种5kg,乙种10kg,丙种10kg混在一起,则售价应定为每千克 .
3.某班40名同学参加“援助汶川大地震”捐款活动,情况如下表所示:
捐款/元 1 2 3 4 5 6
人数/人 4 5 10 x 8 y
请回答以下问题:
(1)用含x,y的代数式表示出该班参加“支持申奥”捐款活动的人平均捐款金额为 ;
(2)若他们平均捐款4元,则x= ,y= .
4.某校举办“汉字听写”大赛15名学生进入决赛,他们所得分数互不相同,比赛共设8个获奖名额,某学生知道自己的分数后,要判断自己能否获奖,他应该关注的统计量是( )
A.平均数 B.中位数 C.众数 D.方差
5.在数据﹣2,0,4,6,9中插入一数据x,使得该组数据的中位数为3,则x= .
6.两组数据m,6,n与1,m,2n,7的平均数都是8,若将这两组数据合并成一组数据,则这组新数据的极差为 .
7.一组正整数数据5,5,7,7,x的中位数与平均数相等,则x的值为 .
二.平均数、中位数、众数、方差例题
8.快要到新年了,某鞋店老板要进一批新年鞋,他一定会参考下面的调查数据,他最关注的是( )
A.中位数 B.平均数 C.加权平均数 D.众数
9.某校“安全知识”比赛有16名同学参加,规定前8名的同学进入决赛.若某同学想知道自己能否晋级,不仅要了解自己的成绩,还需要了解16名参赛同学成绩的( )
A.平均数 B.中位数 C.众数 D.方差
10.某校开展了“好书伴我成长”读书活动,为了解12月份九年级学生的读书情况,随机调查了九年级50名学生读书的册数,统计数据如下表所示,下列说法正确的是( )
册数 0 1 2 3 4
人数 4 12 16 17 1
A.众数是17 B.中位数是2 C.平均数是2 D.方差是2
11.随着冬季的来临,流感进入高发期.某校为有效预防流感,购买了A,B,C,D四种艾条进行消毒,它们的单价分别是30元,25元,20元,18元.四种艾条的购买比例如图所示,那么所购买艾条的平均单价是( )
A.22.5元 B.23.25元 C.21.75元 D.24元
12.某单位定期对员工的专业知识、工作业绩、出勤情况三个方面进行综合考核(考核的满分均为100分),三个方面的重要性之比依次为3:5:2.小王经过考核后所得的各项分数依次为90、88、85分,那么小王的最后综合得分是( )
A.87 B.87.5 C.87.6 D.88
13.比赛中“去掉一个最高分,去掉一个最低分”后,一定不会发生变化的统计量是( )
A.平均数 B.众数 C.中位数 D.极差
14.若在一组数据4,3,2,4,2中再添加一个数后,它们的平均数不变,则添加数据后这组数据的中位数是( )
A.3 B.4 C.3.5 D.4.5
15.在一次数学测验中,甲、乙、丙、丁四位同学的成绩(单位:分)分别是80,x,80,70,若这四位同学成绩的众数与平均数恰好相等,则他们成绩的中位数是( )
A.90分 B.85分 C.80分 D.75分
16.在“传唱红色经典,弘扬爱国精神”比赛中,七位评委给某选手打出7个原始分.如果规定:去掉一个最高分和一个最低分,余下5个有效分的平均值作为这位选手的最后得分,则7个原始分和5个有效分这两组分数相比较,一定不会发生改变的是( )
A.方差 B.极差 C.中位数 D.平均数
17.2021年以来,教育部陆续出台了手机、睡眠、作业、读物、体质等“五项管理”的文件,6月1日发布的《未成年人学校保护规定》也把相关内容纳入其中,将其法治化、制度化.某班人数共有41人,在一次体质测试中,有1人未参加集体测试,老师对集体测试的成绩按40人进行了统计,得到测试成绩分数的平均数是88,中位数是85.缺席集体测试的同学后面进行了补测,成绩为88分,关于该班级41人的体质测试成绩,下列说法正确的是( )
A.平均数不变,中位数变大
B.平均数不变,中位数无法确定
C.平均数变大,中位数变大
D.平均数不变,中位数变小
18.某校航模兴趣小组共有50位同学,他们的年龄分布如表:
年龄/岁 13 14 15 16
人数 5 23 ▃ ▃
由于表格污损,15和16岁人数不清,则下列关于年龄的统计量可以确定的是( )
A.平均数、众数 B.众数、中位数
C.平均数、方差 D.中位数、方差
19.若一组数据5,﹣4,2,x,﹣1的极差为13,则x的值为 .
20.甲、乙两组数据的平均数相同,方差分别为m,n,甲组数据比乙组数据波动小,则m﹣n值为( )
A.正数 B.负数 C.0 D.非负数
21.如果数据x1,x2,…,xn的方差是3,则另一组数据2x1,2x2,…,2xn方差是( )
A.6 B.12 C.3 D.5
22.已知一组数据x1,x2,x3,…xn的方差是3,则另一组数据2x1+3,2x2+3,2x3+3,…2xn+3的方差是 .
23.在对一组样本数据进行分析时,小明列出了方差的计算公式:s2=[(8﹣)2+(6﹣)2+(9﹣)2+(6﹣)2+(11﹣)2],由公式提供的信息,判断下列关于样本的说法错误的是( )
A.平均数是8 B.众数是6 C.中位数是9 D.方差是3.6
24.如果一组数据的方差是S=[(x1﹣20)2+(x2﹣20)2+…+(x12﹣20)2],已知9是这组数据中的一个数据,现把9去掉,则所得新数据的平均数是( )
A.12 B.15 C.18 D.21
25.2022年2月8日,中国选手谷爱凌在冬奥会自由式滑需女子大跳台决赛中夺得金牌,国际滑联评价谷爱凌为滑雪史上第一人,已知自由式滑雪大跳台的计分规则如下:
①每次滑雪的动作,按照其完成难度的不同对应一个难度系数A;
②每次滑雪都有7名裁判进行打分,在7个得分中去掉1个最高分和1个最低分,剩下5个得分的平均值为这次起跳的完成分B;
③运动员该次滑雪的最后得分C=难度系数A×完成分B×3.
在某次自由滑雪大跳台比赛中,某运动员的打分(满分10分)表为:
难度系数 裁判 1 2 3 4 5 6 7
3.0 打分 10 9.5 9 9 9.5 9 9
(1)7名裁判打分的众数是 ;中位数是 .
(2)该运动员的最后得分是多少?
(3)已知某运动员在一次滑雪大跳台比赛中完成了难度系数3.2的动作,且所有裁判都打了满分,请你帮她算一下,难度系数3.2的满分成绩应该是多少分?
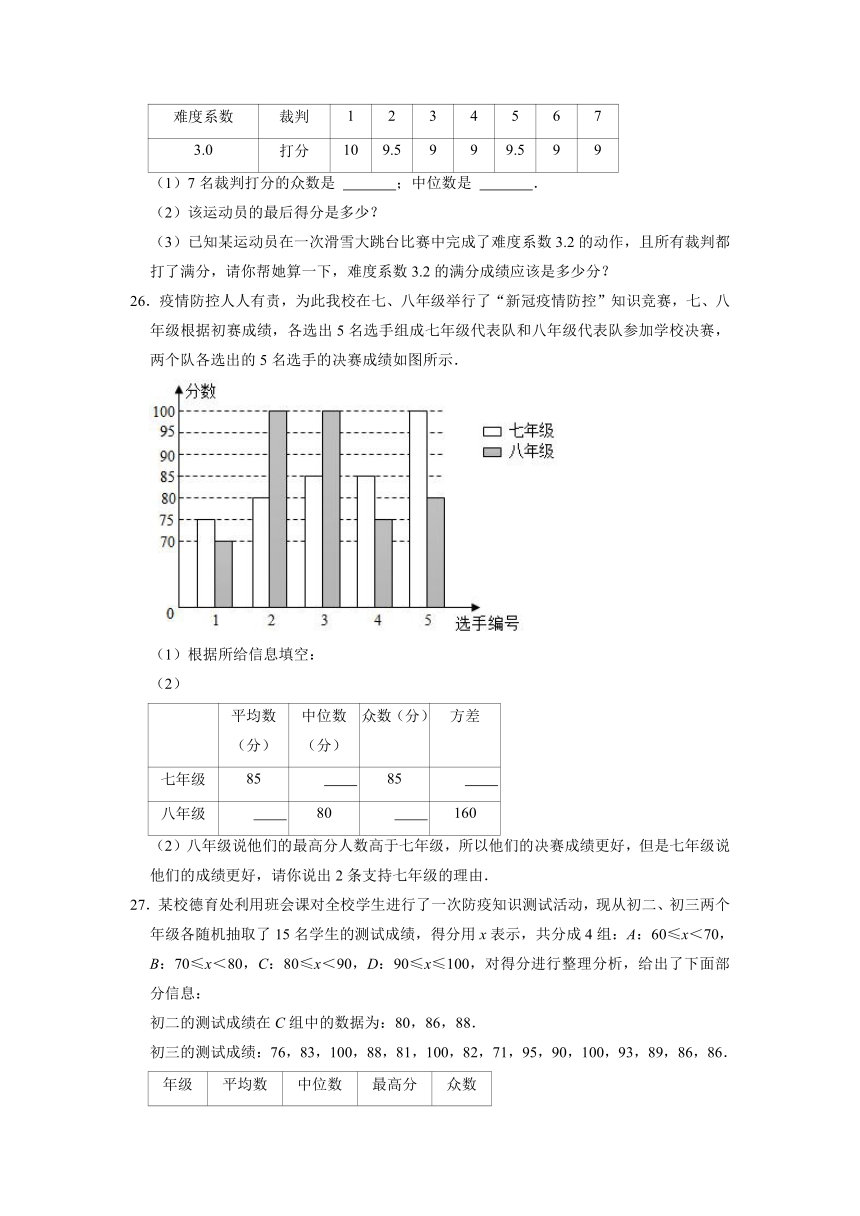
26.疫情防控人人有责,为此我校在七、八年级举行了“新冠疫情防控”知识竞赛,七、八年级根据初赛成绩,各选出5名选手组成七年级代表队和八年级代表队参加学校决赛,两个队各选出的5名选手的决赛成绩如图所示.
根据所给信息填空:
平均数(分) 中位数(分) 众数(分) 方差
七年级 85 85
八年级 80 160
(2)八年级说他们的最高分人数高于七年级,所以他们的决赛成绩更好,但是七年级说他们的成绩更好,请你说出2条支持七年级的理由.
27.某校德育处利用班会课对全校学生进行了一次防疫知识测试活动,现从初二、初三两个年级各随机抽取了15名学生的测试成绩,得分用x表示,共分成4组:A:60≤x<70,B:70≤x<80,C:80≤x<90,D:90≤x≤100,对得分进行整理分析,给出了下面部分信息:
初二的测试成绩在C组中的数据为:80,86,88.
初三的测试成绩:76,83,100,88,81,100,82,71,95,90,100,93,89,86,86.
年级 平均数 中位数 最高分 众数
初二 88 a 98 98
初三 88 88 100 b
(1)a= ,b= ;
(2)通过以上数据分析,你认为 (填“初二”或“初三”)学生对防疫知识的掌握更好?请写出一条理由;
(3)若初二、初三共有3000名学生,请估计此次测试成绩达到90分及以上的学生约有多少人?
28.为加强安全教育,某校开展了“防溺水”安全知识竞赛,想了解七年级学生对“防溺水”安全知识的掌握情况,现从七年级学生中随机抽取50名学生进行竞赛,并将他们的竞赛成绩(百分制)进行整理、描述和分析.部分信息如下:
a.七年级参赛学生成绩频数分布直方图(数据分成五组:50≤x<60,60≤x<70,70≤x<80,80≤x<90,90≤x≤100)如图所示
b.七年级参赛学生成绩在70≤x<80这一组的具体得分是:70 71 73 75 76 76 76 77 77 78 79
c.七年级参赛学生成绩的平均数、中位数、众数如下:
年级 平均数 中位数 众数
七 76.9 m 80
d.七年级参赛学生甲的竞赛成绩得分为79分.
根据以上信息,回答下列问题:
(1)在这次测试中,七年级在75分以上(含75分)的有 人;
(2)表中m的值为 ;
(3)在这次测试中,七年级参赛学生甲的竞赛成绩得分排名年级第 名;
(4)该校七年级学生有500人,假设全部参加此次测试,请估计七年级成绩超过平均数76.9分的人数.
参考答案
一.易错题
1.解:∵(105﹣15)÷30=90÷30=3,
∴求出的平均数与实际平均数的差是﹣3,
故选:D.
2.解:根据题意售价应该定为=7.2(元/千克),
故答案为7.2元.
3.解:(1)由已知得平均捐款金额为:
=.
(2)依题意有=4,即4x+6y=76.
又4+5+10+x+8+y=40,x+y=13.
联立组成方程组,解得x=1,y=12.
4.解:∵进入决赛的15名学生所得分数互不相同,(15+1)÷2=8,
∴这15名学生所得分数的中位数即是获奖的学生中的最低分,
∴某学生知道自己的分数后,要判断自己能否获奖,他应该关注的统计量是中位数,
如果这名学生的分数大于或等于中位数,则他能获奖,
如果这名学生的分数小于中位数,则他不能获奖.
故选:B.
5.解:在数据﹣2,0,4,6,9中插入一数据x,这6个数从小到大排列处在中间位置的两个数的平均数3,即中位数为3,
所以=3,
解得,x=2,
故答案为:2.
6.解:∵两组数据m,6,n与1,m,2n,7的平均数都是8,
∴,
解得:,
故将这两组数据合并成一组数据为:12,6,6,1,12,12,7,
则极差为:12﹣1=11.
故答案为:11.
7.解:当x≤5时,由题意得:(5+5+7+7+x)=5,解得:x=1;
当5<x<7时:(5+5+7+7+x)=x,解得x=6;
当x≥7时,由题意得:(5+5+7+7+x)=7,解得x=11.
所以x的值为1或6或11.
故答案为1或6或11.
二.平均数、中位数、众数、方差例题
8.解:因为快要到新年了,某鞋店老板要进一批新年鞋,他最关注的是哪种型号的销量最好,
所以必须关注众数.
故选:D.
9.解:共有16名学生参加预赛,取前8名,所以某同学需要知道自己的成绩是否进入前8.我们把所有同学的成绩按大小顺序排列,
第8名与第9名的平均成绩是这组数据的中位数,所以某同学知道这组数据的中位数,才能知道自己是否进入决赛.
故选:B.
10.解:观察表格,可知这组样本数据的平均数为:
(0×4+1×12+2×16+3×17+4×1)÷50=;
∵这组样本数据中,3出现了17次,出现的次数最多,
∴这组数据的众数是3;
∵将这组样本数据按从小到大的顺序排列,其中处于中间的两个数都是2,
∴这组数据的中位数为2,
故选:B.
11.解:由图可得,
所购买艾条的平均单价是:=21.75(元),
故选:C.
12.解:由题意可得,
小王的最后综合得分是:=88(分),
故选:D.
13.解:比赛中“去掉一个最高分,去掉一个最低分”后,一定不会发生变化的统计量是中位数,
故选:C.
14.解:(4+3+2+4+2)÷5
=15÷5
=3.
∵它们的平均数不变,
∴添加的数据为3.
∴这组新数据为:2,2,3,3,4,4,
这组新数据的中位数为:×(3+3)=3,
故选:A.
15.解:①x=80时,众数是80,平均数=(80+80+80+70)÷4≠80,则此情况不成立,
②x=70时,众数是80和70,而平均数是一个数,则此情况不成立,
③x≠70且x≠80时,众数是80,根据题意得:
(80+x+80+70)÷4=80,
解得x=90,
则中位数是(80+80)÷2=80.
故选:C.
16.解:根据题意,从7个原始评分中去掉1个最高分和1个最低分,得到5个有效评分.5个有效评分与7个原始评分相比,不变的是中位数.
故选:C.
17.解:∵缺席集体测试的同学的成绩和其他40人的平均数相同,都是88分,
∴该班41人的测试成绩的平均分为88分不变,中位数是从小到大第21个人的成绩,原来是第20个和第21个人成绩的平均数,中位数可能不变,可能变大,故
中位数无法确定.
故选:B.
18.解:一共有50人,中位数是从小到大排列后处在第25、26位两个数的平均数,而13岁的有5人,14岁的有23人,因此从小到大排列后,处在第25、26位两个数都是14岁,因此中位数是14岁,不会受15岁,16岁人数的影响;
因为14岁有23人,而13岁的有5人,15岁、16岁共有22人,因此众数是14岁;
故选:B.
19.解:当x是最大数时,x﹣(﹣4)=13,解得:x=9;
当x是最小数时,5﹣x=13,解得:x=﹣8.
故x的值为9或﹣8.
故答案为:9或﹣8.
20.解:∵甲、乙两组数据的方差分别为m,n,甲组数据比乙组数据波动小,
∴m<n,
则m﹣n<0,即m﹣n是负数,
故选:B.
21.解:∵数据x1,x2,…,xn的方差是3,
∴另一组数据2x1,2x2,…,2xn方差是22×3=12,
故选:B.
22.解:设这组数据x1,x2,x3,…xn的平均数为,则另一组新数据2x1+3,2x2+3,2x3+3,…2xn+3的平均数为2+3,
∵S2=[(x1﹣)2+(x2﹣)2+…+(xn﹣)2]
=3,
∴方差为S′2=[(2x1+3﹣2﹣3)2+(2x2+3﹣2﹣3)2+…+(2xn+3﹣2﹣3)2]
=[4(x1﹣)2+4(x2﹣)2+…+4(xn﹣)2]
=4×3
=12,
故答案为12.
23.解:由方差的计算公式知,这组数据为6、6、8、9、11,
所以这组数据的平均数为=8,众数为6,中位数为8,
方差为s2=[(8﹣8)2+(6﹣8)2+(9﹣8)2+(6﹣8)2+(11﹣8)2]=3.6,
故选:C.
24.解:由题意知:新数据平均值=(20×12﹣9)÷11=21.
故选:D.
25.解:(1)9.0出现次数最多,7名裁判打分的众数是9;
把这组数据按照从小到大的顺序排列得:9、9、9、9、9.5、9.5、10,根据中位数的定义知,中位数是9.
故答案为:9;9;
(2)3.0××(9.5+9.0+9.0)×3=82.5(分).
故该运动员本次滑雪的得分是82.5分.
(3)3.2××(10+10+10)×3=96(分),
答:难度系数3.2的满分成绩应该是96分.
26.解:(1)七年级5位选手的成绩为75、80、85、85、100,
其中位数为85分,方差为×[(75﹣85)2+(80﹣85)2+2×(85﹣85)2+(100﹣85)2]=70,
八年级5位选手的成绩为70、75、80、100、100,
所以其平均数为=85(分),众数为100分,
故答案为:85、70、85、100;
(2)①七年级成绩的方差小于八年级,成绩比八年级稳定;
②七年级的中位数比八年级高,所以七年级成绩好一些.
27.解:(1)由直方图可知,初二的测试成绩15个数据按从小到大的顺序排列,第8个数落在C组的第二个,
∵初二的测试成绩在C组中的数据为:80,86,88,
∴中位数a=86,
∵初的三测试成绩:76,83,71,100,81,100,82,88,95,90,100,86,89,93,86.
∴按从小到大排列是:71,76,81,82,83,86,86,88,89,90,93,95,100,100,100,
∴众数b=100;
故答案为:85,100;
(2)根据以上数据,我认为初三对防疫知识的掌握更好.
理由:两个年级的平均成绩一样,而初三的中位数、最高分、众数均高于初二,说明初三掌握的较好.
故答案为:初三;
(3)3000×=1200(人),
答:此次测试成绩达到90分及以上的约有1200人.
28.解:(1)在这次测试中,七年级在75分以上(含75分)的有8+15+8=31(人),
故答案为:31.
(2)七年级50人成绩的中位数是第25、26个数据的平均数,而第25、26个数据分别为77、78,
∴m==77.5,
故答案为:77.5;
(3)在这次测试中,七年级参赛学生甲的竞赛成绩得分排名年级第24名,
故答案为:24;
(4)估计七年级成绩超过平均数76.9分的人数为500×=270(人).
一.易错题
1.某同学使用计算器求30个数据的平均数时,错将其中的一个数据105输入为15,那么由此求出的平均数与实际平均数的差是( )
A.﹣3.5 B.3 C.0.5 D.﹣3
2.甲、乙、丙三种糖果售价分别为每千克6元,7元,8元,若将甲种5kg,乙种10kg,丙种10kg混在一起,则售价应定为每千克 .
3.某班40名同学参加“援助汶川大地震”捐款活动,情况如下表所示:
捐款/元 1 2 3 4 5 6
人数/人 4 5 10 x 8 y
请回答以下问题:
(1)用含x,y的代数式表示出该班参加“支持申奥”捐款活动的人平均捐款金额为 ;
(2)若他们平均捐款4元,则x= ,y= .
4.某校举办“汉字听写”大赛15名学生进入决赛,他们所得分数互不相同,比赛共设8个获奖名额,某学生知道自己的分数后,要判断自己能否获奖,他应该关注的统计量是( )
A.平均数 B.中位数 C.众数 D.方差
5.在数据﹣2,0,4,6,9中插入一数据x,使得该组数据的中位数为3,则x= .
6.两组数据m,6,n与1,m,2n,7的平均数都是8,若将这两组数据合并成一组数据,则这组新数据的极差为 .
7.一组正整数数据5,5,7,7,x的中位数与平均数相等,则x的值为 .
二.平均数、中位数、众数、方差例题
8.快要到新年了,某鞋店老板要进一批新年鞋,他一定会参考下面的调查数据,他最关注的是( )
A.中位数 B.平均数 C.加权平均数 D.众数
9.某校“安全知识”比赛有16名同学参加,规定前8名的同学进入决赛.若某同学想知道自己能否晋级,不仅要了解自己的成绩,还需要了解16名参赛同学成绩的( )
A.平均数 B.中位数 C.众数 D.方差
10.某校开展了“好书伴我成长”读书活动,为了解12月份九年级学生的读书情况,随机调查了九年级50名学生读书的册数,统计数据如下表所示,下列说法正确的是( )
册数 0 1 2 3 4
人数 4 12 16 17 1
A.众数是17 B.中位数是2 C.平均数是2 D.方差是2
11.随着冬季的来临,流感进入高发期.某校为有效预防流感,购买了A,B,C,D四种艾条进行消毒,它们的单价分别是30元,25元,20元,18元.四种艾条的购买比例如图所示,那么所购买艾条的平均单价是( )
A.22.5元 B.23.25元 C.21.75元 D.24元
12.某单位定期对员工的专业知识、工作业绩、出勤情况三个方面进行综合考核(考核的满分均为100分),三个方面的重要性之比依次为3:5:2.小王经过考核后所得的各项分数依次为90、88、85分,那么小王的最后综合得分是( )
A.87 B.87.5 C.87.6 D.88
13.比赛中“去掉一个最高分,去掉一个最低分”后,一定不会发生变化的统计量是( )
A.平均数 B.众数 C.中位数 D.极差
14.若在一组数据4,3,2,4,2中再添加一个数后,它们的平均数不变,则添加数据后这组数据的中位数是( )
A.3 B.4 C.3.5 D.4.5
15.在一次数学测验中,甲、乙、丙、丁四位同学的成绩(单位:分)分别是80,x,80,70,若这四位同学成绩的众数与平均数恰好相等,则他们成绩的中位数是( )
A.90分 B.85分 C.80分 D.75分
16.在“传唱红色经典,弘扬爱国精神”比赛中,七位评委给某选手打出7个原始分.如果规定:去掉一个最高分和一个最低分,余下5个有效分的平均值作为这位选手的最后得分,则7个原始分和5个有效分这两组分数相比较,一定不会发生改变的是( )
A.方差 B.极差 C.中位数 D.平均数
17.2021年以来,教育部陆续出台了手机、睡眠、作业、读物、体质等“五项管理”的文件,6月1日发布的《未成年人学校保护规定》也把相关内容纳入其中,将其法治化、制度化.某班人数共有41人,在一次体质测试中,有1人未参加集体测试,老师对集体测试的成绩按40人进行了统计,得到测试成绩分数的平均数是88,中位数是85.缺席集体测试的同学后面进行了补测,成绩为88分,关于该班级41人的体质测试成绩,下列说法正确的是( )
A.平均数不变,中位数变大
B.平均数不变,中位数无法确定
C.平均数变大,中位数变大
D.平均数不变,中位数变小
18.某校航模兴趣小组共有50位同学,他们的年龄分布如表:
年龄/岁 13 14 15 16
人数 5 23 ▃ ▃
由于表格污损,15和16岁人数不清,则下列关于年龄的统计量可以确定的是( )
A.平均数、众数 B.众数、中位数
C.平均数、方差 D.中位数、方差
19.若一组数据5,﹣4,2,x,﹣1的极差为13,则x的值为 .
20.甲、乙两组数据的平均数相同,方差分别为m,n,甲组数据比乙组数据波动小,则m﹣n值为( )
A.正数 B.负数 C.0 D.非负数
21.如果数据x1,x2,…,xn的方差是3,则另一组数据2x1,2x2,…,2xn方差是( )
A.6 B.12 C.3 D.5
22.已知一组数据x1,x2,x3,…xn的方差是3,则另一组数据2x1+3,2x2+3,2x3+3,…2xn+3的方差是 .
23.在对一组样本数据进行分析时,小明列出了方差的计算公式:s2=[(8﹣)2+(6﹣)2+(9﹣)2+(6﹣)2+(11﹣)2],由公式提供的信息,判断下列关于样本的说法错误的是( )
A.平均数是8 B.众数是6 C.中位数是9 D.方差是3.6
24.如果一组数据的方差是S=[(x1﹣20)2+(x2﹣20)2+…+(x12﹣20)2],已知9是这组数据中的一个数据,现把9去掉,则所得新数据的平均数是( )
A.12 B.15 C.18 D.21
25.2022年2月8日,中国选手谷爱凌在冬奥会自由式滑需女子大跳台决赛中夺得金牌,国际滑联评价谷爱凌为滑雪史上第一人,已知自由式滑雪大跳台的计分规则如下:
①每次滑雪的动作,按照其完成难度的不同对应一个难度系数A;
②每次滑雪都有7名裁判进行打分,在7个得分中去掉1个最高分和1个最低分,剩下5个得分的平均值为这次起跳的完成分B;
③运动员该次滑雪的最后得分C=难度系数A×完成分B×3.
在某次自由滑雪大跳台比赛中,某运动员的打分(满分10分)表为:
难度系数 裁判 1 2 3 4 5 6 7
3.0 打分 10 9.5 9 9 9.5 9 9
(1)7名裁判打分的众数是 ;中位数是 .
(2)该运动员的最后得分是多少?
(3)已知某运动员在一次滑雪大跳台比赛中完成了难度系数3.2的动作,且所有裁判都打了满分,请你帮她算一下,难度系数3.2的满分成绩应该是多少分?
26.疫情防控人人有责,为此我校在七、八年级举行了“新冠疫情防控”知识竞赛,七、八年级根据初赛成绩,各选出5名选手组成七年级代表队和八年级代表队参加学校决赛,两个队各选出的5名选手的决赛成绩如图所示.
根据所给信息填空:
平均数(分) 中位数(分) 众数(分) 方差
七年级 85 85
八年级 80 160
(2)八年级说他们的最高分人数高于七年级,所以他们的决赛成绩更好,但是七年级说他们的成绩更好,请你说出2条支持七年级的理由.
27.某校德育处利用班会课对全校学生进行了一次防疫知识测试活动,现从初二、初三两个年级各随机抽取了15名学生的测试成绩,得分用x表示,共分成4组:A:60≤x<70,B:70≤x<80,C:80≤x<90,D:90≤x≤100,对得分进行整理分析,给出了下面部分信息:
初二的测试成绩在C组中的数据为:80,86,88.
初三的测试成绩:76,83,100,88,81,100,82,71,95,90,100,93,89,86,86.
年级 平均数 中位数 最高分 众数
初二 88 a 98 98
初三 88 88 100 b
(1)a= ,b= ;
(2)通过以上数据分析,你认为 (填“初二”或“初三”)学生对防疫知识的掌握更好?请写出一条理由;
(3)若初二、初三共有3000名学生,请估计此次测试成绩达到90分及以上的学生约有多少人?
28.为加强安全教育,某校开展了“防溺水”安全知识竞赛,想了解七年级学生对“防溺水”安全知识的掌握情况,现从七年级学生中随机抽取50名学生进行竞赛,并将他们的竞赛成绩(百分制)进行整理、描述和分析.部分信息如下:
a.七年级参赛学生成绩频数分布直方图(数据分成五组:50≤x<60,60≤x<70,70≤x<80,80≤x<90,90≤x≤100)如图所示
b.七年级参赛学生成绩在70≤x<80这一组的具体得分是:70 71 73 75 76 76 76 77 77 78 79
c.七年级参赛学生成绩的平均数、中位数、众数如下:
年级 平均数 中位数 众数
七 76.9 m 80
d.七年级参赛学生甲的竞赛成绩得分为79分.
根据以上信息,回答下列问题:
(1)在这次测试中,七年级在75分以上(含75分)的有 人;
(2)表中m的值为 ;
(3)在这次测试中,七年级参赛学生甲的竞赛成绩得分排名年级第 名;
(4)该校七年级学生有500人,假设全部参加此次测试,请估计七年级成绩超过平均数76.9分的人数.
参考答案
一.易错题
1.解:∵(105﹣15)÷30=90÷30=3,
∴求出的平均数与实际平均数的差是﹣3,
故选:D.
2.解:根据题意售价应该定为=7.2(元/千克),
故答案为7.2元.
3.解:(1)由已知得平均捐款金额为:
=.
(2)依题意有=4,即4x+6y=76.
又4+5+10+x+8+y=40,x+y=13.
联立组成方程组,解得x=1,y=12.
4.解:∵进入决赛的15名学生所得分数互不相同,(15+1)÷2=8,
∴这15名学生所得分数的中位数即是获奖的学生中的最低分,
∴某学生知道自己的分数后,要判断自己能否获奖,他应该关注的统计量是中位数,
如果这名学生的分数大于或等于中位数,则他能获奖,
如果这名学生的分数小于中位数,则他不能获奖.
故选:B.
5.解:在数据﹣2,0,4,6,9中插入一数据x,这6个数从小到大排列处在中间位置的两个数的平均数3,即中位数为3,
所以=3,
解得,x=2,
故答案为:2.
6.解:∵两组数据m,6,n与1,m,2n,7的平均数都是8,
∴,
解得:,
故将这两组数据合并成一组数据为:12,6,6,1,12,12,7,
则极差为:12﹣1=11.
故答案为:11.
7.解:当x≤5时,由题意得:(5+5+7+7+x)=5,解得:x=1;
当5<x<7时:(5+5+7+7+x)=x,解得x=6;
当x≥7时,由题意得:(5+5+7+7+x)=7,解得x=11.
所以x的值为1或6或11.
故答案为1或6或11.
二.平均数、中位数、众数、方差例题
8.解:因为快要到新年了,某鞋店老板要进一批新年鞋,他最关注的是哪种型号的销量最好,
所以必须关注众数.
故选:D.
9.解:共有16名学生参加预赛,取前8名,所以某同学需要知道自己的成绩是否进入前8.我们把所有同学的成绩按大小顺序排列,
第8名与第9名的平均成绩是这组数据的中位数,所以某同学知道这组数据的中位数,才能知道自己是否进入决赛.
故选:B.
10.解:观察表格,可知这组样本数据的平均数为:
(0×4+1×12+2×16+3×17+4×1)÷50=;
∵这组样本数据中,3出现了17次,出现的次数最多,
∴这组数据的众数是3;
∵将这组样本数据按从小到大的顺序排列,其中处于中间的两个数都是2,
∴这组数据的中位数为2,
故选:B.
11.解:由图可得,
所购买艾条的平均单价是:=21.75(元),
故选:C.
12.解:由题意可得,
小王的最后综合得分是:=88(分),
故选:D.
13.解:比赛中“去掉一个最高分,去掉一个最低分”后,一定不会发生变化的统计量是中位数,
故选:C.
14.解:(4+3+2+4+2)÷5
=15÷5
=3.
∵它们的平均数不变,
∴添加的数据为3.
∴这组新数据为:2,2,3,3,4,4,
这组新数据的中位数为:×(3+3)=3,
故选:A.
15.解:①x=80时,众数是80,平均数=(80+80+80+70)÷4≠80,则此情况不成立,
②x=70时,众数是80和70,而平均数是一个数,则此情况不成立,
③x≠70且x≠80时,众数是80,根据题意得:
(80+x+80+70)÷4=80,
解得x=90,
则中位数是(80+80)÷2=80.
故选:C.
16.解:根据题意,从7个原始评分中去掉1个最高分和1个最低分,得到5个有效评分.5个有效评分与7个原始评分相比,不变的是中位数.
故选:C.
17.解:∵缺席集体测试的同学的成绩和其他40人的平均数相同,都是88分,
∴该班41人的测试成绩的平均分为88分不变,中位数是从小到大第21个人的成绩,原来是第20个和第21个人成绩的平均数,中位数可能不变,可能变大,故
中位数无法确定.
故选:B.
18.解:一共有50人,中位数是从小到大排列后处在第25、26位两个数的平均数,而13岁的有5人,14岁的有23人,因此从小到大排列后,处在第25、26位两个数都是14岁,因此中位数是14岁,不会受15岁,16岁人数的影响;
因为14岁有23人,而13岁的有5人,15岁、16岁共有22人,因此众数是14岁;
故选:B.
19.解:当x是最大数时,x﹣(﹣4)=13,解得:x=9;
当x是最小数时,5﹣x=13,解得:x=﹣8.
故x的值为9或﹣8.
故答案为:9或﹣8.
20.解:∵甲、乙两组数据的方差分别为m,n,甲组数据比乙组数据波动小,
∴m<n,
则m﹣n<0,即m﹣n是负数,
故选:B.
21.解:∵数据x1,x2,…,xn的方差是3,
∴另一组数据2x1,2x2,…,2xn方差是22×3=12,
故选:B.
22.解:设这组数据x1,x2,x3,…xn的平均数为,则另一组新数据2x1+3,2x2+3,2x3+3,…2xn+3的平均数为2+3,
∵S2=[(x1﹣)2+(x2﹣)2+…+(xn﹣)2]
=3,
∴方差为S′2=[(2x1+3﹣2﹣3)2+(2x2+3﹣2﹣3)2+…+(2xn+3﹣2﹣3)2]
=[4(x1﹣)2+4(x2﹣)2+…+4(xn﹣)2]
=4×3
=12,
故答案为12.
23.解:由方差的计算公式知,这组数据为6、6、8、9、11,
所以这组数据的平均数为=8,众数为6,中位数为8,
方差为s2=[(8﹣8)2+(6﹣8)2+(9﹣8)2+(6﹣8)2+(11﹣8)2]=3.6,
故选:C.
24.解:由题意知:新数据平均值=(20×12﹣9)÷11=21.
故选:D.
25.解:(1)9.0出现次数最多,7名裁判打分的众数是9;
把这组数据按照从小到大的顺序排列得:9、9、9、9、9.5、9.5、10,根据中位数的定义知,中位数是9.
故答案为:9;9;
(2)3.0××(9.5+9.0+9.0)×3=82.5(分).
故该运动员本次滑雪的得分是82.5分.
(3)3.2××(10+10+10)×3=96(分),
答:难度系数3.2的满分成绩应该是96分.
26.解:(1)七年级5位选手的成绩为75、80、85、85、100,
其中位数为85分,方差为×[(75﹣85)2+(80﹣85)2+2×(85﹣85)2+(100﹣85)2]=70,
八年级5位选手的成绩为70、75、80、100、100,
所以其平均数为=85(分),众数为100分,
故答案为:85、70、85、100;
(2)①七年级成绩的方差小于八年级,成绩比八年级稳定;
②七年级的中位数比八年级高,所以七年级成绩好一些.
27.解:(1)由直方图可知,初二的测试成绩15个数据按从小到大的顺序排列,第8个数落在C组的第二个,
∵初二的测试成绩在C组中的数据为:80,86,88,
∴中位数a=86,
∵初的三测试成绩:76,83,71,100,81,100,82,88,95,90,100,86,89,93,86.
∴按从小到大排列是:71,76,81,82,83,86,86,88,89,90,93,95,100,100,100,
∴众数b=100;
故答案为:85,100;
(2)根据以上数据,我认为初三对防疫知识的掌握更好.
理由:两个年级的平均成绩一样,而初三的中位数、最高分、众数均高于初二,说明初三掌握的较好.
故答案为:初三;
(3)3000×=1200(人),
答:此次测试成绩达到90分及以上的约有1200人.
28.解:(1)在这次测试中,七年级在75分以上(含75分)的有8+15+8=31(人),
故答案为:31.
(2)七年级50人成绩的中位数是第25、26个数据的平均数,而第25、26个数据分别为77、78,
∴m==77.5,
故答案为:77.5;
(3)在这次测试中,七年级参赛学生甲的竞赛成绩得分排名年级第24名,
故答案为:24;
(4)估计七年级成绩超过平均数76.9分的人数为500×=270(人).
