第九单元总复习(课件)人教版五年级数学下册(共29张PPT)
文档属性
| 名称 | 第九单元总复习(课件)人教版五年级数学下册(共29张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 768.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-07 00:00:00 | ||
图片预览








文档简介
(共29张PPT)
总复习
人教版五年级数学下册
1
目录
观察物体(三)
2
图形的运动(三)
3
长方体和正方体
4
因数和倍数
5
分数的意义和性质
6
分数的加、减法
7
折线统计图
8
找次品
观察物体(三)
根据从同一个方向看到的形状,可以摆出不同的几何组合体
从正面看到的形状
根据三视图确定立体图形:
先从一个方向看到的形状分析,推测可能出现的各种情况;
再结合从其他两个方向看到的形状综合分析;
最后确定立体图形。
练一练
仓库里有一堆正方体形状的纸箱,从三个不同方位看到的形状如下图。
正面
左面
上面
这堆纸箱可能有( )个
9或10
是由( )个小正方体搭成的。
4
图形的运动(三)
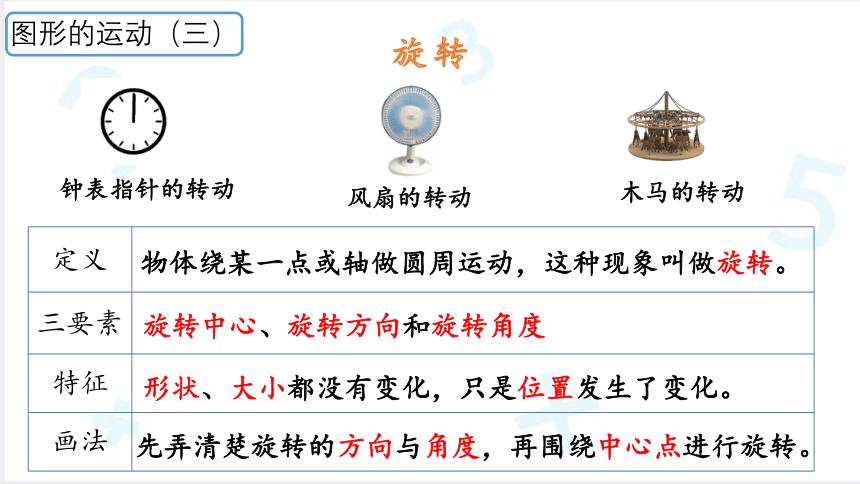
旋转
定义
三要素
特征
画法
物体绕某一点或轴做圆周运动,这种现象叫做旋转。
旋转中心、旋转方向和旋转角度
形状、大小都没有变化,只是位置发生了变化。
钟表指针的转动
风扇的转动
木马的转动
先弄清楚旋转的方向与角度,再围绕中心点进行旋转。
练一练
钟面上时针从12时开始,按顺时针方向旋转90°后指向( )时,按逆时针方向旋转90°后指向( )时。
下列现象,既有平移现象,又有旋转现象的是( )。
A.正在工作的风扇叶片 B.运行中的观光电梯
C.在笔直道路上行驶的汽车 D.传输带上的物品
3
9
C
练一练
将下面的图形绕点O分别顺时针旋转90°,逆时针旋转90°。
O
逆时针旋转90°
顺时针旋转90°
长方体和正方体
6个面、12条棱和8个顶点
相对的2个面完全相同,相对的4条棱长度相等。
一般由6个长方形组成,特殊情况下有2个相对的面是正方形。
表面积=(长×宽+长×高+宽×高)×2 S=2(ab+ah+bh)
体积=长×宽×高=底面积×高 V=abh=Sh
棱长和=(长+宽+高)×4 C=4(a+b+h)
与体积的计算方法相同,但要从容器里面量长、宽、高。
特征
表面积
体积
棱长和
容积
练一练
如右图,长方体最大的面长为( )cm,宽为( )cm,面积是( )cm ;最小的面长为( )cm,宽为( )cm,面积是( )cm ;棱长和为( )cm。
25cm
20cm
18cm
25
20
500
20
18
360
252
做一节长为1.6m,宽和高都是10cm的铁皮通风管,至少需要铁皮( )平方厘米。
一个长方体的药水箱里装了60升的药水,已知药水箱里面长为5分米,宽为3分米,药水深为( )分米
6400
4
长方体和正方体
6个面、12条棱和8个顶点
6个面完全相同,12条棱长度相等。
6个面都是正方形。
表面积=棱长×棱长×6 S=6a2
体积=棱长×棱长×棱长=底面积×高 V=a3=Sh
棱长和=棱长×12 C=12a
与体积的计算方法相同,但要从容器里面量棱长。
练一练
一个正方体的棱长总和是72cm,它的6个面都是边长为( )cm的正方形,它的表面积是( )cm ,体积是( )cm 。
至少要( )个同样的小正方体才能拼成一个大正方体,如果一个小正方体的棱长是5cm,那么大正方体的表面积是( )cm ,体积是( )cm 。
把3个棱长都是4cm的正方体拼成一个长方体,表面积减少了( )cm ,它的体积是( )cm 。
6
216
216
8
600
1000
64
192
长方体和正方体
长度单位
面积单位
体积单位
容积单位
千米(km) 米(m) 分米(dm) 厘米(cm)
相邻长度单位之间的进率是10。
平方米(m2) 平方分米(dm2) 平方厘米(cm2) 相邻面积单位之间的进率是100。
立方米(m3) 立方分米(dm3) 立方厘米(cm3) 相邻体积单位之间的进率是1000。
1L=1000mL 1dm3=1L 1cm3=1mL
大单位变小单位,数变大,乘进率。
小单位变大单位,数变小,除以进率。
练一练
2.4m=( )dm 340cm=( )m
0.6dm3=( )cm3 530dm2=( )m2
3.2立方分米=( )升=( )毫升
3立方分米40立方厘米=( )立方分米
24
3.4
600
5.3
3.2
3200
3.04
因数和倍数
定义:
在整数除法中,如果商是整数且没有余数,我们就说除数是被除数的因数(也称约数),被除数是除数的倍数。
如:
12÷2=6,我们就说2和6是12的因数,12 是2和6的倍数。
特征:
一个数的最小因数是1,最大因数是它本身;
一个数的最小倍数是它本身,没有最大倍数。
一个数的因数的个数是有限的,一个数的倍数的个数是无限的。
因数和倍数
3的倍数特征:
一个数各位上数的和是3的倍数。
5的倍数特征:
个位上是0或5的数。
2的倍数特征:
个位上是0、2、4、6或8的数。
奇数
偶数
最小的奇数是1
最小的偶数是2
因数和倍数
按因数的个数
质数
合数
只有1和它本身两个因数。
除了1和它本身还有别的因数。
1
最小是2
最小是4
质数×质数=合数
奇数+偶数=奇数
奇数+奇数=偶数
偶数+偶数=偶数
练一练
填空
一个数比10小,是奇数,又是3的倍数,它是( )。
一个数的最大因数是36,这个数是( ),这个数的最小倍数是( )。
三个连续奇数的和是45,这三个奇数分别是( )、( )和( )。
判断
36是0.9的倍数。 ( )
24÷8=3,8和3是因数,24是倍数。 ( )
3或9
36
36
13
15
17
×
×
分数的意义和性质
定义:
一个物体、一个计量单位或一些物体都可以看作一个整体,把这个整体平均分成若干份,这样的一份或几份可以用分数来表示。
分数单位:
把单位“1”平均分成若干份,表示其中一份的数叫做分数单位。
分母是几,分数单位就是几分之一。
分子是几,就有几个分数单位。
分数的意义和性质
小数
分数
被除数÷除数=(除数≠0)
分子÷分母,除不尽的保留两位小数
分母是10、100、1000的,可直接写成小数
写成分母是10、100、1000的分数,再约分
分数与除法的关系:
分数与小数的互化:
分数的意义和性质
分数
真分数:分子小于分母;真分数<1。
带分数:由整数(0除外)和真分数组成。
假分数:分子大于或等于分母;假分数≥1。
假分数
整数或真分数
分子÷分母
分数的意义和性质
公因数:
几个数公有的因数;其中最大的叫做它们的最大公因数。
几个数公有的倍数;其中最小的叫做它们的最小公倍数。
公倍数:
特殊情况:
两个数为互质数:它们的最大公因数是1;最小公倍数是两个数的乘积。
两个数为倍数关系:它们的最大公因数为较小数,最小公倍数是较大数。
分数的意义和性质
分数的基本性质:
分数的分子和分母同时乘或者除以相同的数(0除外),分数的大小不变。
应用
约分:把一个分数化成和它相等,但分子和分母都比较小的分数。
方法:分子和分母同时除以它们的公因数。化成最简分数
通分:把异分母分数分别化成和原来分数相等的同分母分数。
方法:用异分母的最小公倍数作为公分母,分母乘几,分子也乘几。
练一练
表示把单位“1”平均分成( )份,取其中的( )份;还表示把4平均分成( )份,取其中的( )份。
的分数单位是( ),至少添上( )个这样的分数单位就变成了一个整数。
分母是8的最简真分数有( )。
=30÷( )=( )(小数)
把2kg糖平均分成5份,每份是总数的( ),是( )kg。
20分=( )小时 1m13cm=( )m
7
4
7
1
1
、、、
25
1.2
分数的加、减法
同分母分数相加、减,分母不变,只把分子相加、减。
异分母分数相加、减,先通分,然后按照同分母分数加、减法进行计算。
计算的结果能约分的要约成最简分数。
分数加减法与整数加减法的混合运算顺序和运算定律一样。
练一练
=
= 1
=
=11
=2
=
+
= +
=1
=
折线统计图
单式折线统计图只能看出一组数据变化的整体趋势。
复式折线统计图可以比较方便地比较两组数据的变化趋势。
画复式折线统计图时,要先确定图例,按照图例画。
练一练
(1)统计某城市2015年各月降水变化情况适合用( )统计图;统计2015年10月我国部分城市降水情况适合用( )统计图。
(2)( )统计图不但可以表示出数量的多少,而且能清楚地表示出数量的增减变化情况。
(3)如果要反映两地下半年平均每月的气温变化对比情况,应选用( )统计图。
折线
条形
折线
复式折线
找次品
找次品的最佳方法:分成3份,尽量平均分,不能平均分的,最多与最少相差1。这时称的次数最少。
要辨别的物品数目 保证能找出次品至少需要称的次数
2-3 4-9 10-27 28-81 82-243 …… 1
2
3
4
5
……
再见!
总复习
人教版五年级数学下册
1
目录
观察物体(三)
2
图形的运动(三)
3
长方体和正方体
4
因数和倍数
5
分数的意义和性质
6
分数的加、减法
7
折线统计图
8
找次品
观察物体(三)
根据从同一个方向看到的形状,可以摆出不同的几何组合体
从正面看到的形状
根据三视图确定立体图形:
先从一个方向看到的形状分析,推测可能出现的各种情况;
再结合从其他两个方向看到的形状综合分析;
最后确定立体图形。
练一练
仓库里有一堆正方体形状的纸箱,从三个不同方位看到的形状如下图。
正面
左面
上面
这堆纸箱可能有( )个
9或10
是由( )个小正方体搭成的。
4
图形的运动(三)
旋转
定义
三要素
特征
画法
物体绕某一点或轴做圆周运动,这种现象叫做旋转。
旋转中心、旋转方向和旋转角度
形状、大小都没有变化,只是位置发生了变化。
钟表指针的转动
风扇的转动
木马的转动
先弄清楚旋转的方向与角度,再围绕中心点进行旋转。
练一练
钟面上时针从12时开始,按顺时针方向旋转90°后指向( )时,按逆时针方向旋转90°后指向( )时。
下列现象,既有平移现象,又有旋转现象的是( )。
A.正在工作的风扇叶片 B.运行中的观光电梯
C.在笔直道路上行驶的汽车 D.传输带上的物品
3
9
C
练一练
将下面的图形绕点O分别顺时针旋转90°,逆时针旋转90°。
O
逆时针旋转90°
顺时针旋转90°
长方体和正方体
6个面、12条棱和8个顶点
相对的2个面完全相同,相对的4条棱长度相等。
一般由6个长方形组成,特殊情况下有2个相对的面是正方形。
表面积=(长×宽+长×高+宽×高)×2 S=2(ab+ah+bh)
体积=长×宽×高=底面积×高 V=abh=Sh
棱长和=(长+宽+高)×4 C=4(a+b+h)
与体积的计算方法相同,但要从容器里面量长、宽、高。
特征
表面积
体积
棱长和
容积
练一练
如右图,长方体最大的面长为( )cm,宽为( )cm,面积是( )cm ;最小的面长为( )cm,宽为( )cm,面积是( )cm ;棱长和为( )cm。
25cm
20cm
18cm
25
20
500
20
18
360
252
做一节长为1.6m,宽和高都是10cm的铁皮通风管,至少需要铁皮( )平方厘米。
一个长方体的药水箱里装了60升的药水,已知药水箱里面长为5分米,宽为3分米,药水深为( )分米
6400
4
长方体和正方体
6个面、12条棱和8个顶点
6个面完全相同,12条棱长度相等。
6个面都是正方形。
表面积=棱长×棱长×6 S=6a2
体积=棱长×棱长×棱长=底面积×高 V=a3=Sh
棱长和=棱长×12 C=12a
与体积的计算方法相同,但要从容器里面量棱长。
练一练
一个正方体的棱长总和是72cm,它的6个面都是边长为( )cm的正方形,它的表面积是( )cm ,体积是( )cm 。
至少要( )个同样的小正方体才能拼成一个大正方体,如果一个小正方体的棱长是5cm,那么大正方体的表面积是( )cm ,体积是( )cm 。
把3个棱长都是4cm的正方体拼成一个长方体,表面积减少了( )cm ,它的体积是( )cm 。
6
216
216
8
600
1000
64
192
长方体和正方体
长度单位
面积单位
体积单位
容积单位
千米(km) 米(m) 分米(dm) 厘米(cm)
相邻长度单位之间的进率是10。
平方米(m2) 平方分米(dm2) 平方厘米(cm2) 相邻面积单位之间的进率是100。
立方米(m3) 立方分米(dm3) 立方厘米(cm3) 相邻体积单位之间的进率是1000。
1L=1000mL 1dm3=1L 1cm3=1mL
大单位变小单位,数变大,乘进率。
小单位变大单位,数变小,除以进率。
练一练
2.4m=( )dm 340cm=( )m
0.6dm3=( )cm3 530dm2=( )m2
3.2立方分米=( )升=( )毫升
3立方分米40立方厘米=( )立方分米
24
3.4
600
5.3
3.2
3200
3.04
因数和倍数
定义:
在整数除法中,如果商是整数且没有余数,我们就说除数是被除数的因数(也称约数),被除数是除数的倍数。
如:
12÷2=6,我们就说2和6是12的因数,12 是2和6的倍数。
特征:
一个数的最小因数是1,最大因数是它本身;
一个数的最小倍数是它本身,没有最大倍数。
一个数的因数的个数是有限的,一个数的倍数的个数是无限的。
因数和倍数
3的倍数特征:
一个数各位上数的和是3的倍数。
5的倍数特征:
个位上是0或5的数。
2的倍数特征:
个位上是0、2、4、6或8的数。
奇数
偶数
最小的奇数是1
最小的偶数是2
因数和倍数
按因数的个数
质数
合数
只有1和它本身两个因数。
除了1和它本身还有别的因数。
1
最小是2
最小是4
质数×质数=合数
奇数+偶数=奇数
奇数+奇数=偶数
偶数+偶数=偶数
练一练
填空
一个数比10小,是奇数,又是3的倍数,它是( )。
一个数的最大因数是36,这个数是( ),这个数的最小倍数是( )。
三个连续奇数的和是45,这三个奇数分别是( )、( )和( )。
判断
36是0.9的倍数。 ( )
24÷8=3,8和3是因数,24是倍数。 ( )
3或9
36
36
13
15
17
×
×
分数的意义和性质
定义:
一个物体、一个计量单位或一些物体都可以看作一个整体,把这个整体平均分成若干份,这样的一份或几份可以用分数来表示。
分数单位:
把单位“1”平均分成若干份,表示其中一份的数叫做分数单位。
分母是几,分数单位就是几分之一。
分子是几,就有几个分数单位。
分数的意义和性质
小数
分数
被除数÷除数=(除数≠0)
分子÷分母,除不尽的保留两位小数
分母是10、100、1000的,可直接写成小数
写成分母是10、100、1000的分数,再约分
分数与除法的关系:
分数与小数的互化:
分数的意义和性质
分数
真分数:分子小于分母;真分数<1。
带分数:由整数(0除外)和真分数组成。
假分数:分子大于或等于分母;假分数≥1。
假分数
整数或真分数
分子÷分母
分数的意义和性质
公因数:
几个数公有的因数;其中最大的叫做它们的最大公因数。
几个数公有的倍数;其中最小的叫做它们的最小公倍数。
公倍数:
特殊情况:
两个数为互质数:它们的最大公因数是1;最小公倍数是两个数的乘积。
两个数为倍数关系:它们的最大公因数为较小数,最小公倍数是较大数。
分数的意义和性质
分数的基本性质:
分数的分子和分母同时乘或者除以相同的数(0除外),分数的大小不变。
应用
约分:把一个分数化成和它相等,但分子和分母都比较小的分数。
方法:分子和分母同时除以它们的公因数。化成最简分数
通分:把异分母分数分别化成和原来分数相等的同分母分数。
方法:用异分母的最小公倍数作为公分母,分母乘几,分子也乘几。
练一练
表示把单位“1”平均分成( )份,取其中的( )份;还表示把4平均分成( )份,取其中的( )份。
的分数单位是( ),至少添上( )个这样的分数单位就变成了一个整数。
分母是8的最简真分数有( )。
=30÷( )=( )(小数)
把2kg糖平均分成5份,每份是总数的( ),是( )kg。
20分=( )小时 1m13cm=( )m
7
4
7
1
1
、、、
25
1.2
分数的加、减法
同分母分数相加、减,分母不变,只把分子相加、减。
异分母分数相加、减,先通分,然后按照同分母分数加、减法进行计算。
计算的结果能约分的要约成最简分数。
分数加减法与整数加减法的混合运算顺序和运算定律一样。
练一练
=
= 1
=
=11
=2
=
+
= +
=1
=
折线统计图
单式折线统计图只能看出一组数据变化的整体趋势。
复式折线统计图可以比较方便地比较两组数据的变化趋势。
画复式折线统计图时,要先确定图例,按照图例画。
练一练
(1)统计某城市2015年各月降水变化情况适合用( )统计图;统计2015年10月我国部分城市降水情况适合用( )统计图。
(2)( )统计图不但可以表示出数量的多少,而且能清楚地表示出数量的增减变化情况。
(3)如果要反映两地下半年平均每月的气温变化对比情况,应选用( )统计图。
折线
条形
折线
复式折线
找次品
找次品的最佳方法:分成3份,尽量平均分,不能平均分的,最多与最少相差1。这时称的次数最少。
要辨别的物品数目 保证能找出次品至少需要称的次数
2-3 4-9 10-27 28-81 82-243 …… 1
2
3
4
5
……
再见!
