代数式[上学期]

课件24张PPT。用字母表示数授课人：雷　达
课件制作人：雷　达第三章 字母表示数思考：自己随便想一个自然数，将这个数乘5减 7，再把结果乘2加14，那么最后结果的个位数是多少？2（5x – 7）+ 14字母能表示什么一只青蛙1张嘴，2只眼睛4条腿，1声扑通跳下水；
二只青蛙2张嘴，4只眼睛8条腿，2声扑通跳下水；
三只青蛙3张嘴，6只眼睛12条腿，3声扑通跳下水；
四只青蛙 张嘴， 只眼睛 条腿， 声扑通跳下水；
……
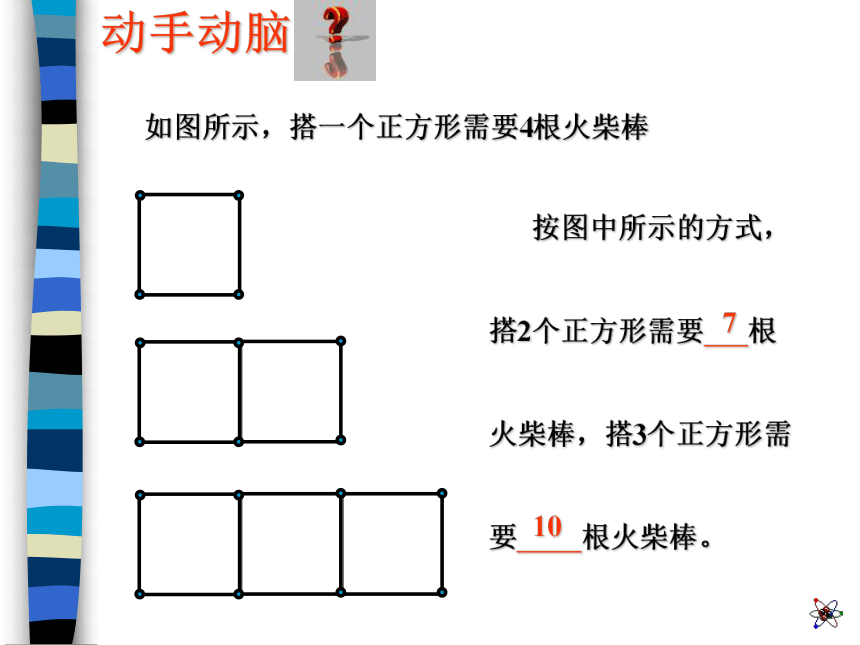
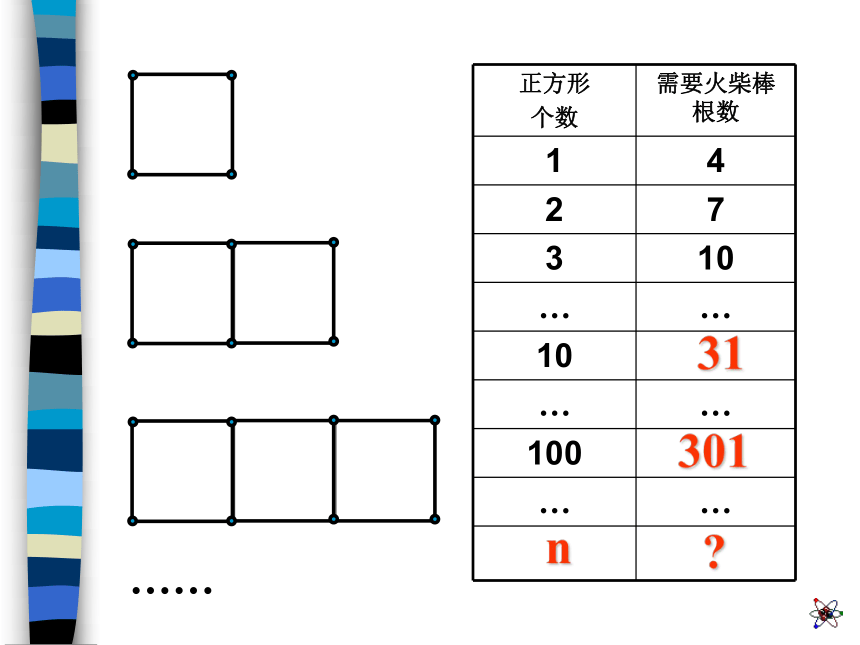
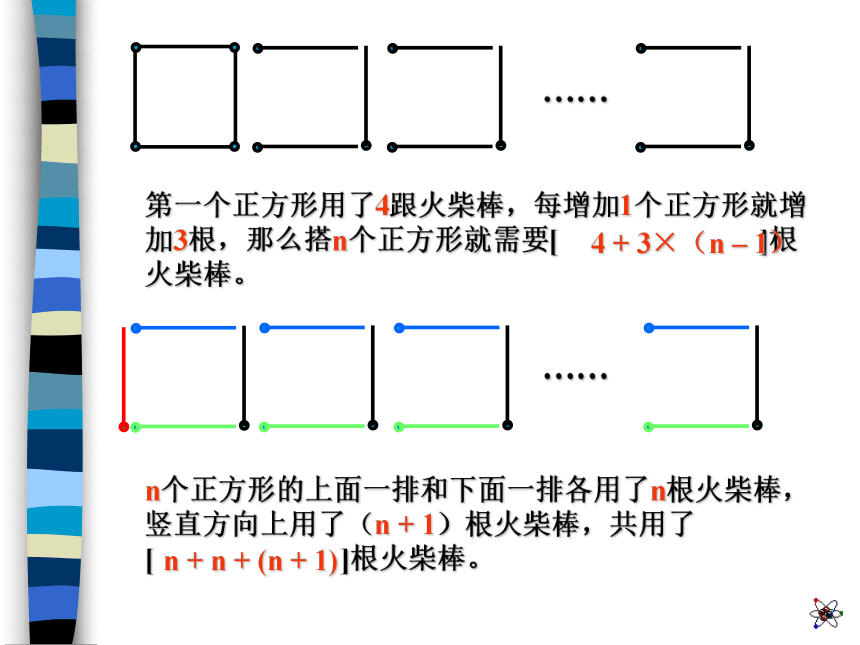
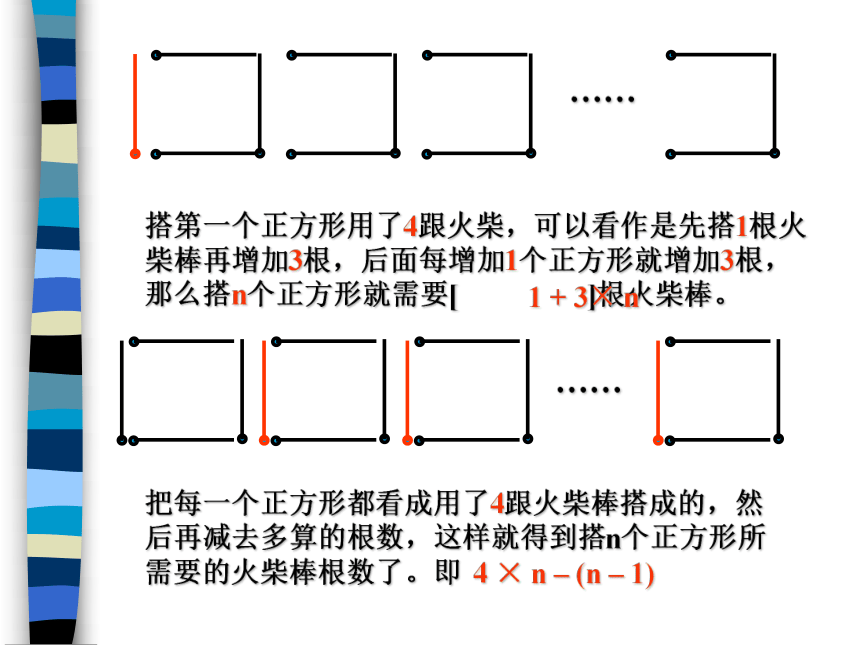
n只青蛙 张嘴， 只眼睛 条腿， 声扑通跳下水；48164nn 用字母n表示青蛙的数量之后，上述关系就可简洁地表示为“n只青蛙有n张嘴，2 × n只眼睛，4 × n条腿，n声扑通跳下水”数学与生活 按图中所示的方式，搭2个正方形需要 根火柴棒，搭3个正方形需要 根火柴棒。如图所示，搭一个正方形需要4根火柴棒710动手动脑……?30131n第一个正方形用了4跟火柴棒，每增加1个正方形就增加3根，那么搭n个正方形就需要[ ]根火柴棒。n个正方形的上面一排和下面一排各用了n根火柴棒，竖直方向上用了（n + 1）根火柴棒，共用了 [ ]根火柴棒。…………4 + 3×（n – 1）n + n + (n + 1)搭第一个正方形用了4跟火柴，可以看作是先搭1根火柴棒再增加3根，后面每增加1个正方形就增加3根，那么搭n个正方形就需要[ ]根火柴棒。把每一个正方形都看成用了4跟火柴棒搭成的，然后再减去多算的根数，这样就得到搭n个正方形所需要的火柴棒根数了。即…………1 + 3× n4 × n – (n – 1) 一般地，数字与字母、字母与字母、数字或字母与括号相乘时，乘号通常简写作“·”或者省略不写，数字与数字相乘仍用乘号连接。 一般把数字写在字母前面；若式子中有带分数相乘，一定要把带分数写成假分数的式。有多个字母相乘写成省略乘号的形式时，字母按照英文字母的排列顺序摆放。如：4×a可以写作 4·a 或者4a 4×4就只能写成4×4，其中乘号不能写
成“·”或者省略。如： ×b×a×c可以写作 abc 4 + 3×（n – 1）
1 + 3× n
4 × n – (n – 1)4 + 3（n – 1）
1 + 3n
4n – (n – 1)根据你的计算方法：搭200个这样的正方形需要多少根火柴棒呢？4 + 3 ×（200 – 1）= 601用字母表示数的优点：
1、简明性；2、任意性如果用a、b、c分别表示有理数，那么有理数的
运算定律可表示成：加法交换律：a + b = b + a
加法结合律：(a + b) + c =a + (b + c)
乘法交换律：a · b = b · a
乘法结合律：(a · b) · c =a · (b · c)
乘法分配律：a(b + c) = ab + ac 路程公式：路程 = 时间 × 速度
如果用表示s路程，表示v速度，表示t时间，那么
这个路程公式可表示为：用字母表示数时需要注意：
1、在同一问题中，同一字母只能表示同一数量，
不同的数量要用不同的字母表示。
2、用字母表示实际问题中某一数量时，字母的取
值必须使这个问题有意义，并且符合实际。如除
法法则：用表示a、b两个有理数，则s = v·t 或者 s = vt注意其中知识应用随堂练习：
1、明明步行上学，速度为v米/秒；亮亮骑自行车
上学，速度是明明的3倍，则亮亮的速度可以表示
为 米/秒。2、如图，用字母表示图中阴影部分的面积。mn – pq3v活动与探究：（1）（2）（3）1、填写下表：2、第n个图形有多少个小三角形？149162536n2课堂小结：你知道了什么？1、一般地，数字与字母、字母与字母、数字或
字母与代括号相乘时，乘号通常简写作“·”或者省
略不写，数字与数字相乘仍用乘号连接。
2、一般把数字写在字母前面；若式子中有带分
数相乘，一定要把带分数写成假分数的形式。
有多个字母相乘写成省略乘号的形式时，字母按
照英文字母的排列顺序摆放。
3、在实际问题中含有单位时，如果运算结果是
和的形式，要把整个的式子括起来再写单位。作业：课本P104 No.1谢谢观摩指导 按图中所示的方式，搭2个正方形需要 根火柴棒，搭3个正方形需要 根火柴棒。代数式710n=1，N=4n=2，N=4 + 3n=3，N=4 + 3 + 3思考：当n=10、100时呢，搭像这样的正方形需要多少根火柴棒？N = 4 + 3( n – 1 )像4+3（ x – 1 ）、x+x+(x+1)、a+b、ab、2(m+n)、 等式子都是代数式。单独一个数或一个字母也是代数式。填空：
1、边长为a厘米的正方形的周长是厘米，面积为厘米；
2、小华、小明的速度分别是x米/分钟、y米/分钟，6分钟后他们一共走了米；
3、温度有2摄氏度上升t摄氏度后是；
4、小亮用秒走了米，他的速度是米/秒；
5、小彬拿166元钱去买钢笔，买了单价为5元的钢笔n枝，则剩下的钱为元，他最多能买这种钢笔枝。列代数式时需注意：
1、数字与字母、字母与字母、数字或字母与代括号相乘时，乘号通常简写作“·”或者省略不写。一般把数字写在字母前面；若代数式中有带分数相乘，一定要把带分数写成假分数的形式。数字与数字相乘仍用乘号连接。有多个字母相乘写成省略乘号的形式时，字母按照英文字母的排列顺序摆放。
2、在实际问题中含有单位时，如果运算结果是和的形式，要把整个的代数式括起来再写单位。如：
3、在代数式中出现除法运算时，一般按照分数的写法来写。[例1] 列代数式，并求值：
（1）某公园的门票价格是：成人票每张10元，学生票每张5元。一个旅游团有成人人，学生人，那么该旅行团应付多少门票费？
（2）如果该旅游团有37个成人、15个学生，那么他们应付多少门票费？解：（1）该旅行团应付的门票是（10x + 5y）元。
（2）把=37，=15带入代数式10x + 5y，得
1037 + 515 = 445
代数式还可以表示什么？如果用[例2] 在某地，人们发现某种蟋蟀叫的次数与温度之间有如下的近似关系：用蟋蟀1分叫的次数除以7，然后再加上3，就近似地得到该地当时的温度（）
（1）用代数式表示该地当时的温度；
（2）当蟋蟀1分叫的次数分别是80，100和120时，该地当时的温度约是多少？解：（1）用c表示蟋蟀1分叫的次数，则该地当时的温度为
（2）把c = 80，100和120分别代入，得
因此，当蟋蟀1分叫的次数分别是80，100和120时，该地当时的温度大约是14，17和20。[例3] （1）张宇身高1.2米，在某时测得他的影子的长度是2米，此时张宇的身高是他影子长的多少倍？
（2）如果用L表示物体的影子，那么如何用代数式表示此时此地物体的高度？
（3）该地某建筑物影长5.5米，此时它的高度是多少米？解：（1）