多边形外角和[下学期]
图片预览




文档简介
课件11张PPT。初一数学组 义务教育课程标准实验教科书多边形的内角和与外角和思考?2. n边形的内角和为_______________。
它揭示了多边形的_______和_____间的
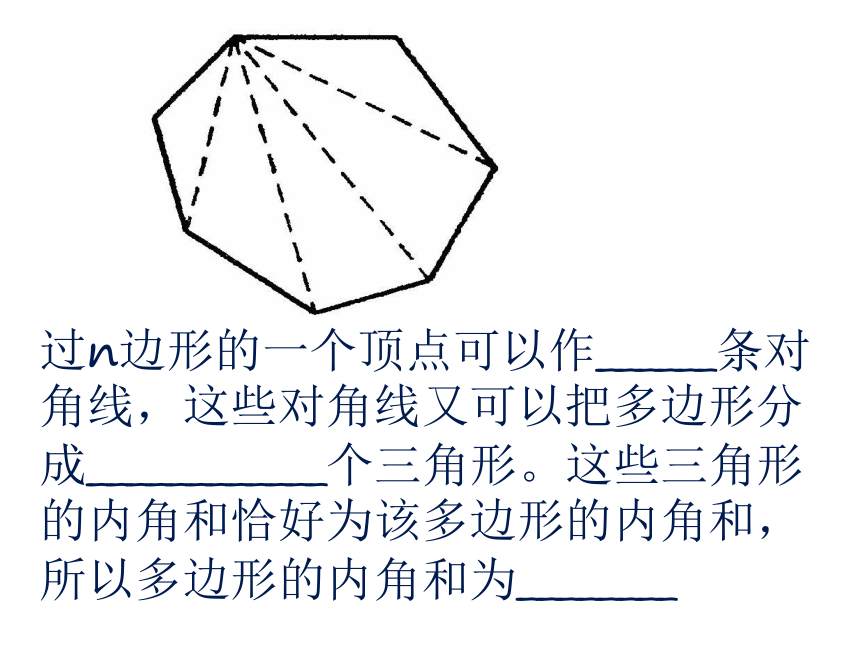
关系,当边数增加1时,内角和增加___1. n边形共有________条对角线。3. n边形的内角和是如何推导的?过n边形的一个顶点可以作______条对角线,这些对角线又可以把多边形分成____________个三角形。这些三角形的内角和恰好为该多边形的内角和,所以多边形的内角和为________4. 那么n边形的外角和为?又如何推导?多边形的外角和:与多边形的每个内角相邻的外角分别有两个,这两个外角是对顶角.从与每个内角相邻的两个外角中分别取一个相加,得到的和称为多边形的外角和. ∠1 +∠2+ ∠3+ ∠4怎样求多边形的外角和?思考?提示:
想想三角形的外角和是怎么求的?任意多边形的外角和都为_______,
与多边形的变数________。360°无关习题精选4.多边形的内角中至少应有________个锐角。2.若多边形的边数从3增加到10,则其外角和的度数____________________1.一个多边形的每一个外角都等于40°,则它是_________边形3.一个多边形的内角和与外角和的度数之比是9:2,则这是一个________边形挑战!!!留给你的挑战小结多边形的内角和为 (n-2)·180°
任意多边形的外角和为360°若一个多边形的内角和与某一个外角的度数和为1350°,求这个外角的度数及多边形的条数。谢 谢 !
它揭示了多边形的_______和_____间的
关系,当边数增加1时,内角和增加___1. n边形共有________条对角线。3. n边形的内角和是如何推导的?过n边形的一个顶点可以作______条对角线,这些对角线又可以把多边形分成____________个三角形。这些三角形的内角和恰好为该多边形的内角和,所以多边形的内角和为________4. 那么n边形的外角和为?又如何推导?多边形的外角和:与多边形的每个内角相邻的外角分别有两个,这两个外角是对顶角.从与每个内角相邻的两个外角中分别取一个相加,得到的和称为多边形的外角和. ∠1 +∠2+ ∠3+ ∠4怎样求多边形的外角和?思考?提示:
想想三角形的外角和是怎么求的?任意多边形的外角和都为_______,
与多边形的变数________。360°无关习题精选4.多边形的内角中至少应有________个锐角。2.若多边形的边数从3增加到10,则其外角和的度数____________________1.一个多边形的每一个外角都等于40°,则它是_________边形3.一个多边形的内角和与外角和的度数之比是9:2,则这是一个________边形挑战!!!留给你的挑战小结多边形的内角和为 (n-2)·180°
任意多边形的外角和为360°若一个多边形的内角和与某一个外角的度数和为1350°,求这个外角的度数及多边形的条数。谢 谢 !
